Ciencia, Investigación, Academia y Desarrollo

Ingeniería, 2003-00-00 vol:8 nro:1 pág:29-35

La programación mixta como herramienta para la solución de problemas de Planeación Agregada Multietapas

Dusko Kalenatic

Miembro grupo de investigación GIP Universidad Católica de Colombia.

César A. López B.

Miembro grupo de investigación MMAI Universidad Distrital Francisco José de Caldas.

Leonardo J. González R.

Miembro grupo de investigación MMAI Universidad Distrital Francisco José de Caldas y GIP Universidad Católica de Colombia.

Resumen

Este artículo presenta la formulación de un modelo de planeación agregada serial multiperiodo, multiestado, con varias fuentes por etapa de proceso, incluyendo costos cóncavos y decisiones de escasez (entregas tardías) de producto terminado, el cual puede ser solucionado mediante técnicas de programación entera mixta.

Palabras clave: Planeación agregada, Multiperiodo, Multiestado, Costos cóncavos, Multifuente, Escasez, Programación entera, Costo de alistamiento7

Abstract

This paper describes, the development and testing of a mathematical programming model of serial multiperiod ag gregate production planning, multistage, with various sources for process stage, including concave cost and backlogging decision of finished product, the problem may be solved with mixed integer programming approaches.

Key words: Aggregate planning, Multiperiod, Multistage, Concave cost, Multisource, backlogging, Integer programming, Set-up cost

INTRODUCCIÓN

El propósito de los modelos de planeación agregada es establecer los niveles de producción en una unidad de agregación que agrupa familias de productos, con el fin de satisfacer un criterio de decisión como por ejemplo el de costo mínimo.

La formulación de modelos de optimización para resolver problemas de planeación de la producción varia en función del detalle en que se quiere expresar las variables de decisión, en las unidades de agregación, en los criterios de decisión, y en las limitaciones y restricciones que presenta el sistema real que se pretende modelar.

Existen modelos de planeación agregada de la producción que se formularon con relación al establecimiento de los niveles de la fuerza laboral [1] [2], Otros modelos que consideran niveles de escasez [ 3],[4],[5], se plantean modelos con mayor grado de complejidad en donde se consideran decisiones de establecimiento de niveles de producción en sistemas seriales y niveles de inventario por estado de proceso [ 6],[7] , Y siendo un poco más amplios, con varias fuentes de producción por etapa de proceso [ 8],[9 ] además de la consideración de los costos de alistamiento [10] [11] que causan cambios en la naturaleza del modelo de optimización(costos cóncavos) .

Para la solución de dichos problemas se utilizan técnicas de optimización como la programación lineal y la programación dinámica[ 12],[13] pero en la medida que la complejidad de los modelos se incrementa se convierten en problemas de naturaleza combinatoria[14], lo cual requiere del refinamiento y ampliación de la cobertura de las técnicas y de la utilización de métodos de optimización avanzada. Por estas razones en el presente artículo se plantea un modelo con las siguientes variantes:

• Costos de alistamiento ( Generan concavidad)
• Multietapa multiestado
• Multiperiodo
• Múltiples fuentes por etapa
• Restricciones de capacidad
• Con niveles de escasez ( Solo es posible para producto terminado)

MODELO DE PLANEACIÓN AGREGADA DE LA PRODUCCIÓN MULTIETAPAS CON MÚLTIPLES FUENTES POR ETAPA DE PROCESO, NIVEL DE ESCASEZ Y COSTOS CONCAVOS

OBJETIVO

Determinar un plan de producción para un producto que se fabrica con diferentes fuentes por etapa de proceso con el propósito de obtener un costo mínimo.

FUNCIÓN OBJETIVO

La función objetivo del modelo depende de la cantidad a producir, así como de las cantidades en inventario y de los posibles faltantes que se produzcan durante el horizonte de planeación (1) (3), la función de costo de producción hace parte integral de esta y genera la concavidad del modelo (2) (4)

Función costo de planeación de la producción

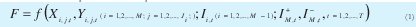
Función costo de producción

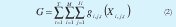
VARIABLES DE DECISIÓN

X_i,j,t :Variable entera que expresa la cantidad a producir en la etapa de proceso "i" con la fuente "j" en el período "t"
i = 1,2,..., M ; j = 1,2,..., J_i y t = 1,2,..., T

Y_{i, j,t} : Variable binaria que expresa la decisión de producir en la etapa de proceso "i" con la fuente "j" en el período "t"
i = 1,2,...,M; j = 1,2,...,J_i y t = 1,2,..., T

I_i,t :Inventario disponible de producto en proceso en el estado "i" al final del período "t"
i = 1, 2,..., M y t = 1, 2,..., T

I⁺ _M,t :Inventario disponible de producto terminado en el estado "M" al final del período "t" t = 1,2,..., T

I^-_M,t :Ordenes Pendientes de producto terminado en el estado "M" al final del período "t" t = 1,2,..., T

PARÁMETROS

d_t :Demanda requerida de producto terminado en el periodo "t", donde: t = 1,2,..., T

C_i,j,t :Costo unitario de producción, en la etapa de proceso "i", si se utiliza la fuente "j", en el período "t", donde:
i = 1,2,..., M ; j = 1,2,...,J_i y t = 1,2,..., T

A_{i, j,t} : Costo de preparación y alistamiento de la etapa de proceso "i", si se emplea la fuente "j", durante el período "t", donde:
i = 1,2,..., M ; j = 1,2,..., J_i y t = 1,2,...,T

Cd_{i, j,t} : Capacidad disponible en la etapa de proceso "i", de la fuente "j", durante el período "t", i = 1,2,..., M ; j = 1,2,..., J_i y t = 1,2,..., T

h_{i, t} : Costo de mantenimiento del inventario si se mantiene una unidad almacenada en el estado "i", durante el período "t", donde: i = 1,2,..., M y t = 1,2,...,T

Ψ: Costo de penalización por unidad pendiente por unidad de tiempo (costo unitario por escasez) aplicado al promedio de ordenes no entregadas a tiempo.

CONDICIONES INICIALES

I _{i, 0}= 0 : Inventario Inicial de productos en proceso en el estado "i", al comienzo del horizonte de planeación. i = 1,2,..., M

I _i,T = 0 :Inventario final deseado de productos en proceso en el estado "i", al final del horizonte de planeación. i = 1,2,..., M

I⁺ _{M, 0}= K₁ (Constante): Inventario inicial de producto terminado en el estado "M", al comienzo del horizonte de planeación.

I⁺ _{M ,T} = K₂ (Constante): Inventario final deseado de producto terminado en el estado "M", al final del horizonte de planeación.

I^-_{M, 0} = 0 : Nivel de escasez o de ordenes pendientes de producto terminado en el estado "M", al comienzo del horizonte de planeación.

I^- _M,T = 0 : Nivel de escasez o de ordenes pendientes de producto terminado en el estado "M", deseado al final del horizonte de planeación.

PARÁMETROS REFERENCIALES

i: Indice que identifica la etapa de proceso y el estado del producto, donde i : i = 1,2,..., M

j: Indice que identifica el tipo de fuente por etapa de proceso, donde j = 1,2,..., J_i

t:Indice que identifica el período de planeación, donde t = 1,2,..., T

M: Número de etapas de proceso y de estados de proceso ( estado final o de producto terminado)

J_i: Número de tipos de fuente por etapa de proceso i = 1,2,..., M

T :Número de períodos del horizonte de planeación

FUNCIÓN OBJETIVO

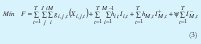
donde:

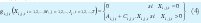
Como la naturaleza de la función es concava entonces se linealiza multiplicando los costos de alistamiento por variables binarias (5) de tal manera que la función objetivo será:

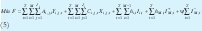
Sujeto a las siguientes restricciones:

Restricciones de Estado

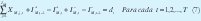
Restricciones de Capacidad

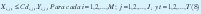
Condiciones Iniciales

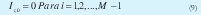
Restricciones Lógicas

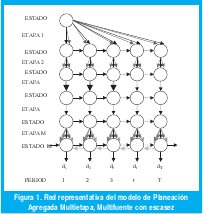
La representacion gráfica del modelo se muestra en la figura 1

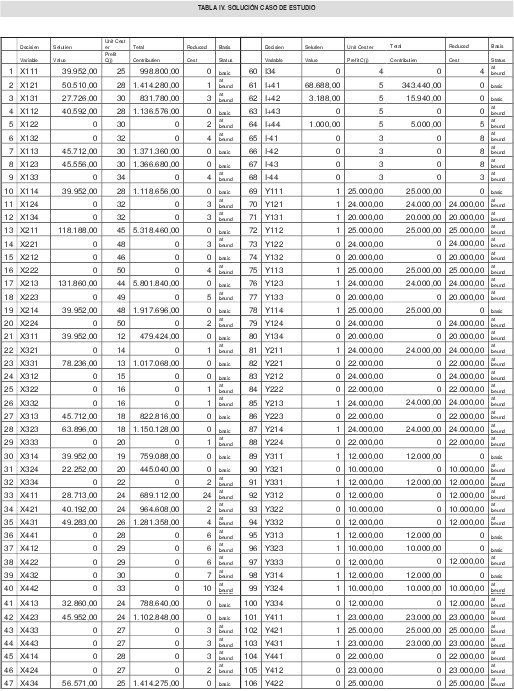
Los resultados obtenidos al utilizar elmodulo de programacion lineal y entera del programa QSBWIN se muestran en la tabla 5

DISCUSIÓN DE RESULTADOS

Para la solución de problemas que presentan estructuras como la del modelo planteado, se propone el enfoque de programación entera mixta [15], y se abre la posibilidad de formular una metodología para resolver problemas de esta naturaleza con otras técnicas asociadas.

Al realizar un análisis a partir de la naturaleza del problema en el sistema real, se da la posibilidad de simplificar y reducir la complejidad del modelo y asi mismo la de la técnica de solución, si por ejemplo, la disponibilidad de los medios de producción no restringe el comportamiento del sistema, entonces, la toma de decisiones solo se fundamentará en los costos asociados a la producción de acuerdo a la demanda requerida[16], es decir se puede considerar que es equivalente a un modelo con capacidad infinita, lo que implica una simplificación en la selección de las fuentes de producción.

Por otra parte, si el sistema de producción esta muy limitado en capacidad , hasta el punto que surge la ne cesidad de producir en todos los períodos de planeación se simplificará la decisión , al poder tratar los costos de alistamiento como costos fijos, y los costos de producción e inventario asociados a los niveles de fabricación como convexos.

Tambien es de considerar, que si los costos de escasez son muy grandes con respecto a los costos de mantenimiento de inventario, podría collevar a una simplificacion del modelo al no considerar la posibilidad de incurrir en escasez.

En contraposición , es posible ampliar la complejidad del modelo [17] [18]si es necesario considerar el modelo como de agregación múltiple (multiproducto) lo que implicaría en gran cantidad de casos la imposibilidad de obtener una solucion inmediata con las técnicas y recursos disponibles.

Es así como, el presente artículo pretende iniciar un proceso de investigación que colleve a el desarrolllo de metodologías y técnicas para la solución de problemas de planeación de la producción agregada de naturaleza combinatoria y por consiguiente de alta complejidad.

Para mostrar la bondad de la técnica de programación entera [19]se formula un caso de estudio que muestra el proceso de formulación, implementación y análisis de resultados.

CONCLUSIONES

El modelo abre la posibilidad de abordar problemas de planeacion agregada de alto gardo de dificultad en entornos manufactureros en sistemas seriales multiestado por medio de programación entera mixta.

La técnica aplicada da soluciones racionales al problema y tiene facilidades en su implementación

Sin embargo las características del problema que pretende resolver este modelo genera dificultades algoritmicas que hacen recomendable la investigación de otras técnicas que mejoren el proceso de solución.

CASO DE ESTUDIO

Modelo de Planeación Agregada múltietapas con múltiples fuentes por etapa con costos de penalización por escasez y con costos de preparación y alistamiento

Una empresa manufacturera elabora la producción de una familia de productos en función de los pedidos y contra inventario, los cuales deben ser fabricados a lo largo de 4 etapas de proceso, para tal efecto cuenta con diferentes tecnologías (tipos de máquina) por etapa de proceso, concretamente se disponen de J₁= 3, J₂=2, J₃= 3 y J₄=4 tipos de máquina (fuentes ) por etapa de proceso respectivamente. La empresa trabaja 6 días por semana de lunes a sábado, no trabaja días feriados, ni la semana santa, además programa vacaciones colectivas los 8 últimos días hábiles del mes de diciembre y los primeros 7 días del mes de enero, en un turno de 8 horas. Adicionalmente se pierde un 20% de la capacidad por factores varios. (Para el cálculo de las capacidades tomar como base el año 2002.)

Para el análisis se recolecto la siguiente información que se muestra en la tabla I, los costos unitarios de producción varían en función del costo de la mano de obra y de los costos de materia prima que aumenta o disminuye de acuerdo a las leyes de oferta y demanda, los costos de alistamiento se conocen por cada tipo de tecnología para cada etapa de proceso, los costos de mantenimiento del inventario varían de acuerdo al estado en que se encuentre el producto, los costos de penalización por ordenes pendientes se permiten y son conocidos.

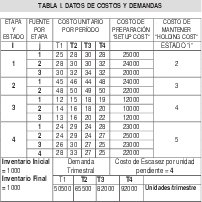
Adicionalmente como condiciones iniciales, no se permite escasez ni al comienzo, ni al final del horizonte de planeación, el inventario inicial de producto terminado y el inventario final deseado se conocen, así como, existe una política de inventario inicial y final de producto en proceso igual a cero (0) y la demanda requerida estimada para cada trimestre.

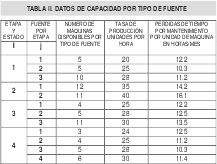
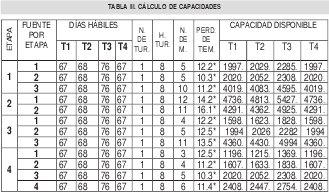
El número de máquinas y las perdidas de tiempo estándar por unidad de máquina para cada tecnología por etapa de proceso, se muestran en la tabla II.

Determinar un plan de producción agregado, que indique el nivel de producción por tipo de fuente para cada etapa de proceso, en nivel de inventario para cada estado, y el nivel de escasez permitido para que el costo de producción sea mínimo.

SOLUCIÓN

Cálculo de capacidades.

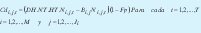
DH :Días Hábiles

NT :Número de turnos

HT : Horas turno.

N _{i, j,t} :Número de máquinas disponibles por etapa de proceso de cada tipo de máquina en cada período de tiempo
t = 1,2,..., T i = 1,2,..., M y j = 1,2,..., J_i

B_{i, j} :Perdidas de tiempo por mantenimiento preventivo por unidad de máquina de cada tipo por etapa de proceso
i = 1,2,..., M y j = 1,2,..., J_i

Fp :Factor de perdida debido a factores externos, no asistencia de los trabajadores a los puestos de trabajo en el momento indicado y por factores organizacionales.

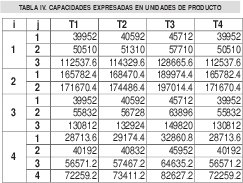
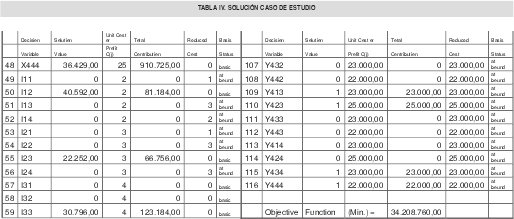
Los cálculos de las capacidades [19] para el caso de estudio se resumen en la tabla III, de tal manera que expresadas en unidades de producto se observan en la tabla IV

Un resumen de la formulación del problema se muestra en la tabla V y los resultados obtenidos en la tabla VI

REFERENCIAS BIBLIOGRÁFICAS

[1] Adam E.,Ebert R. Jr. Administración de la producción y las Operaciones. Prentice Hall. Mexico. 1991

[2] Bedworth D.,Bailey J. E., Integred Production Control Systems, John Wiley & sons, Inc. 1995.

[3] Buffa, E., and Miller J., Production Inventory Systems : Planning and Control. Homewood, IL : Richard d. Irwin, 1979.

[4] Dorea C.E.T. & Hennet J.C., Open-loop and closed-loop production planning for multistage manufacturing systems (00354)

[5] Barthes I. & Hennet J.C., Closed-loop planning of multi-level production under resource constraints ,Proc. 9th Symposium of the IFAC on Information Control in Manufacturing (INCOM'98), Nancy (France), 24-26 Juin 1998, Vol.II, pp.485-490

[6] Falk P.G. Experiments in mixed integer linear programming in a manufacturing system, IPC, New York, USA, 1979

[7] Johnson, L. A., and Montgomery D., Operations Research in Production Planning, Scheduling and Inventory Control. New York: John Wiley & Sons.,1974.

[8] Bird J. Jr., Moore T. The aplication of a product mix Linear Programming Model in corporate policy making. West Virginia University, USA, 1977

[9] Bitran G.R., Hax A.C., The rol of mathematical programmming in production planning, Massachusetts Institute of Technology, 1984

[10] Bowman, E. H., "Production Scheduling by the Transportation Method of Linear Programming" Operations Research, 3, no. 1, 1956.

[11] Hanssmann F., Operations Research in Production and Inventory Systems : Planning and Control. New York : John Wiley & Sons, Inc.,1962

[12] Hennet J.C., A feedback control approach to multistage production planning based on input-output analysis, par J-C. Hennet, 12th International Conference on Input-Output Techniques, New-York (USA), 18-22 Mai 1998.

[13] Silver E.A., Decision Sistems for Inventory Management and Production Planning. New York : John Wiley & Sons. Second Edition, 1985

[14] Ahuja R.K. Network Flows. Prentice Hall. New Yersey. 1993

[15] Schroeder R. G., Administración de Operaciones, Mexico : Mc GRAW-HILL, Tercera Edición,1992

[16] Taha H., Investigación de Operaciones , Mexico, Editorial Alfaomega , Segunda Edición 1991.

[17] Kozan E., An Integrated Production Planning and Control System for Mixed Model Multistage Assembly Processes: An Implementation at the VOLVO Truck Australia, School of Mathematical, Sciences QUT, en: Operation Research in the Third Millenium, , University of Adelaide, DSTO, Adelaide, Australia, September 23-26, 2001

[18] Lawrence K. and Zanakis S., Models and Methods of Production Planning and scheduling, U.S.A.,1984 by the Institute of Industrial engineers.

[19] Rios S., et al. Programación lineal y aplicaciones. Editorial RAMA, Madrid España, 1998

[20] Kalenatic D., Modelo integral y dinamico para el analisis, planeacion, progamacion y control de loas capacidades productivas en empresas manufactureras, Centro de Investigaciones y Desarrollo Cientifico, Universidad Distrital "Francisco josé de Caldas", Bogotá D.C., Colombia ,2001

Dusko Kalenatic
Doctor en Ciencias Tecnicas, Especialista en ingenieria de producción, Economista, Ingeniero en organización, Investigador titular UCC.
dkalenatic@ucatolica.edu.co

Cesar Amilcar López Bello
Ingeniero Industrial, Universidad Distrital. Especialista en Ingeniería de Producción, Universidad Distrital. Magíster en Ingeniería Industrial, Universidad de los Andes. Candidato a Doctor en Ciencias Técnicas, Universidad de Las Villas (Cuba). Profesor Asociado, Facultad de Ingeniería Universidad Distrital. Director de la Maestría en Ingeniería Industrial, Universidad Distrital "Francisco José de Caldas".
cesaralopez@latinmail.com

Leonardo José González Rodríguez
Ingeniero Industrial, Universidad Distrital. Especialista en Ingeniería de Producción, Universidad Distrital. Candidato a Magíster en Ingeniería Industrial, Universidad de los Andes. Profesor Auxiliar, Facultad de Ingeniería. Universidad Distrital "Francisco José de Caldas". le-gonza@uniandes.edu.co,
lejogo@latinmail.com