DOI:
https://doi.org/10.14483/23448393.2858Published:
2008-11-30Issue:
Vol. 8 No. 1 (2003): January - JuneSection:
Science, research, academia and developmentModelamiento difuso con técnicas de Clustering
Keywords:
clustering difuso, centros, función objetivo, matriz de partición, modelo difuso TSK. (es).Downloads
References
L.X.Wang, A Course in Fuzzy Systems and Control. Prentice Hall, 1997.
T. Takagi and M. Sugeno, "Fuzzy Identification of Systems and Its Applications to Modeling and Control", IEEE Trans.on Systems, Man and Cybernetics, vol. SMC-15, No.1, 1985
D. E. Gustafson and W. C. Kessel, "Fuzzy Clustering with a Fuzzy Covariance", Proc.IEEE CDC, pp 761-766, San Diego, CA, USA, 1979
R. Babuska, Fuzzy Modeling for Control. Kluwer Academic Publishers, 1998.
R. Babuska, "et al", "Improved Covariance Estimation for Gustafson-Kessel Clustering", Proc. Of the 2002 IEEE International Conference on Fuzzy Systems,vol. 2, pp. 1081-1085, 2002.
I. Gath and A. B. Geva, "Unsupervised Optimal Fuzzy Clustering", IEEE Trans. On Pattern Analisis and Machine Intelligence, vol. 11, No. 7, pp. 773-781, 1989.
J. C. Bezdek and J. C. Dunn, "Optimal Fuzzy Partitions": A Heuristic for Estimating the Parameters in a Mixture of Normal Distributions, IEEE Trans.on Computers, pp. 835-838, 1975
P. L. Meyer, Probabilidad y Aplicaciones Estadisticas, Addison Wesley, 1992.
J. Abonyi, "et al", "Modified Gath-Geva Fuzzy Clustering for Identification of Takagi-Sugeno Fuzzy Models", IEEE Trans. on Systems, Man and Cybernetic, Part B, October, 2002.
J. Abonyi, "et al", "Identification of Nonlinear System Using Gaussian Mixture of local Models", Hungarian Journal of Industrial Chemestry, vol. 29, 134-139, 2001.
How to Cite
APA
ACM
ACS
ABNT
Chicago
Harvard
IEEE
MLA
Turabian
Vancouver
Download Citation
Ciencia, Investigación, Academia y Desarrollo
Ingeniería, 2003-00-00 vol:8 nro:1 pág:86-94
Modelamiento difuso con técnicas de Clustering
Diana Marcela González Chaparro
Miembro Grupo de Investigación Laboratorio de Automática, Microelectrónica e Inteligencia Computacional LAMIC,de la Universidad Distrial.
Sergio Barato Quintero
Miembro Grupo de Investigación Laboratorio de Automática, Microelectrónica e Inteligencia Computacional LAMIC,de la Universidad Distrial.
Resumen
En este documento se presentan técnicas para derivar modelos difusos Takagi-Sugeno-Kang (TSK) de sistemas complejos, no lineales y semidesconocidos a partir de métodos de clustering (agrupamiento). Se utilizan tres algoritmos: GustafsonKessel (GK), Maximum Likelihood Estimation (MLE) y una modificación a la versión simplificada del algoritmo de Maximum Likelihood. Estos son evaluados en condiciones de presencia ruido. De los resultados de las simulaciones se demostró que el algoritmo menos vulnerable ante ruido es el GK. Adicionalmente, se encontró que en condiciones de poco ruido la generación de submodelos lineales eficientemente se obtuvo con el algoritmo MLE modificado.
Palabras clave: clustering difuso, centros, función objetivo, matriz de partición, modelo difuso TSK.
I. INTRODUCCIÓN
Es de gran importancia el desarrollo de modelos matemáticos de sistemas reales. Estos permiten obtener simulaciones, analizar el comportamiento del sistema y diseñar procesos. Sin embargo, muchos sistemas físicos no son tratables por aproximaciones desde el punto de vista de modelamiento convencional, debido a la falta de conocimiento del sistema, fuerte comportamiento no lineal, y alto grado de incertidumbre.
El modelamiento difuso ha sido reconocido como una poderosa herramienta en el tratamiento de sistemas que presentan los problemas mencionados, debido a la capacidad de integrar información de diferentes fuentes tales como, conocimiento de expertos, modelos empíricos o mediciones. Los conjuntos difusos sirven como interfaz entre las variables cualitativas, los datos numéricos, las entradas y salidas del sistema. Entre las metodologías de identificación difusa se encuentran las técnicas de clustering. Estas se basan en el manejo de datos de entrada y salida del sistema, y su agrupamiento en subconjuntos (clusters). Como gran ventaja, estas técnicas presentan la capacidad de sobrellevar los problemas de no linealidades y la falta de conocimiento preciso del sistema.
II. IDENTIFICACIÓN Y MODELAMIENTO DIFUSO
Las técnicas y algoritmos para el reconocimiento de los parámetros de un modelo de dato se conocen como identificación difusa. Los parámetros de una estructura difusa como funciones de pertenencia y el peso de las reglas son sintonizadas usando los datos de entrada y salida. En este proceso no se hace necesario un conocimiento a priori, en lugar de ello se espera que las funciones de pertenencia y reglas extraídas proporcionen una interpretación del comportamiento del sistema. La identificación es vista como una descomposición de un sistema no lineal, lo cual genera un balance entre la complejidad (no uniforme) y la exactitud del modelo.
El modelamiento difuso reúne el procesamiento lógico de información con estructuras matemáticas capaces de representar mapeos no lineales complejos. La estructura basada en reglas de los sistemas difusos, contribuye a los modelos difusos generados por tratamiento de datos, ya que generan una descripción cualitativa, que combinada con el conocimiento de expertos ayuda a comprender, validar y/o simplificar el modelo.
III. MODELOS TSK
Los modelos TSK son modelos difusos que constan de reglas Ri con la siguiente estructura [1] [2] [9] [10]:
Ri: Si x es Ai entonces yi = aiTx +bi i = 1,2,,K (1)
Donde x es el vector de entrada, Ai es el conjunto difuso (multidimensional), yi es la salida de la i-esima regla, ai es un vector paramétrico y bi es el desplazamiento escalar. La proposición de entrada x es Ai puede ser expresada como una combinación lógica de proposiciones unidimensionales definidas por cada componente del vector de entrada x:
Ri: Si x1 es Ai1 y...y xp es Aip entonces yi = aiTx +bi (2)
Tal como en los modelos difusos Mamdani el grado de cumplimiento de la regla esta dado por
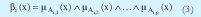
Donde ˆ representa una T-norma[1][4]. La salida del sistema TSK es obtenida combinando las reglas de la siguiente forma:
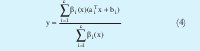
Tomando la normalización del grado de cumplimento como:
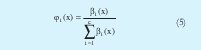
La ecuación (4) se puede rescribir como:

La anterior expresión muestra que los modelos TSK puede cumplir el papel de regresores de funciones, es decir pueden aproximar con cierto margen de exactitud cualquier función y = f(x).
IV. TECNICAS DE CLUSTERING
Las técnicas de clustering surgieron dentro de la disciplina patrones de reconocimiento. Esta técnica busca hallar subgrupos con cierto grado de similaridad dentro de una colección de datos. Además de identificar cada subgrupo, determina los parámetros representativos de cada uno. Originalmente se planteó la idea de que cada dato solo podría pertenecer a un solo subgrupo, denominado hard clustering. Mas adelante se tomó la idea de clustering difuso en el cual particionamiento de datos se hace de forma tal que la transición entre conjuntos es gradual en lugar de abrupta como lo haría el hard clustering [3]-[4]. Para el estudio, la similaridad es definida como una distancia, la cual puede ser medida entre vectores que contienen los datos y un elemento prototipo del cluster, normalmente el centro [4].
Existen varios algoritmos de clustering los cuales tienen en cuenta: la forma geométrica, densidad y relación espacial de cada cluster, además de la distancia entre ellos [3][4]. Se encuentran algoritmos iterativos basados en la optimización de una función objetivo diferenciable, con la cual se mide la conveniencia de la partición. En este documento se trabaja sobre este tipo específico de algoritmos. Una de las primeras técnicas de agrupamiento planteada que utiliza una función objetivo es conocida como Fuzzy C-means [4]. Una desventaja de esta técnica es que la medida de similaridad entre datos genera clusters circulares. En este artículo se trabajan tres algoritmos: Gustafson-Kessel, Maximum Likelihood, y una modificación a la versión simplificada del Maximum Likelihood. Los dos primeros proponen una distancia adaptiva con el fin de detectar clusters de diferentes formas geométricas y orientación, es decir, generan clusters hiperelipsoidales que pueden ser aproximados a hiperplanos. La desventaja de estos algoritmos es que al derivar los antecedentes (funciones de pertenencia) que forman el modelo TSK, se producen errores por proyección o poca interpretabilidad cuado se corrige este error. El tercer algoritmo maneja clusters de forma hiperelipsoidal pero paralelos a los ejes de las variables de entrada. Debido a esto no se producen errores al derivar los antecedentes teniendo una alta interpretabilidad; la desventaja es que se pierde predictividad de modelo.
A. ALGORITMO GUSTAFSON-KESSEL
Este algoritmo se basa en la optimización de la siguiente función objetivo [3][4][5]:
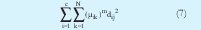
Donde c es el número de clusters, N es el número de datos que se toman de la dispersión, µik es la función de pertenencia del k-esimo dato al i-esimo cluster, m es un índice que indica la fusividad entre las fronteras de cada cluster. Entre más alto sea m más difusas son las fronteras de cada cluster y dij2 es una distancia (norma) entre puntos denominada norma Mahalanobis, la cual es de la siguiente forma:
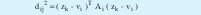
Donde zk, es un vector columna de dimensión s que contiene el k-ésimo dato tomado, vi también es un vector columna de dimensión s denominado centro del cluster y Ai es una matriz simétrica cuyo tamaño es (s x s), esta matriz indica la orientación de cada cluster. En este caso la norma Mahalanobis mide la distancia entre el k-ésimo dato zk y el centro del i-ésimo cluster vi.
En el momento de minimizar se toman como variables µik, Ai y vi, teniendo en cuenta las siguientes restricciones [4][5]:

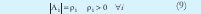
Donde ρi es denominado el volumen de cada cluster.
Para minimizar (7) con las restricciones (8) y (9) se utilizan multiplicadores de Lagrange. Sin las restricciones la minimización conduciría a respuestas triviales µ ik = 0 y Ai = 0. La primera restricción implica que la suma de los grados de pertenencia de cada dato a los clusters debe ser igual a uno, lo cual es acorde con la teoría de probabilidad. La segunda limita el volumen de cada cluster a un valor determinado.
El proceso de minimización se realiza de forma alternante, es decir, se minimiza una variable suponiendo las otras constantes y se iguala a cero. Como resultado la minimización se obtiene las siguientes expresiones, sobre las cuales se realiza el proceso iterativo.
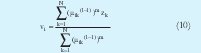
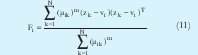
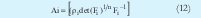
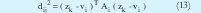
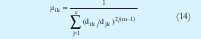
Las iteraciones inician determinando el número de cluster c, el exponente m (por lo general es 2) y seleccionando de manera aleatoria la matriz de partición difusa U de tamaño (c x N) la cual contiene los grados de pertenencia de los datos y cumple con (8). La matriz de partición difusa se encuentra organizada así:

Posteriormente se calcula el valor de los centros con (10). Teniendo el valor de vi se calcula la matriz de covarianza difusa Fi. A partir de (12) se calcula Ai necesaria para hallar la distancia de la expresión (13). La ecuación (13) describe una hiperelipse rotada. La dirección y dimensión de cada uno de los ejes rotados está establecida por los autovectores y autovalores de la matriz Ai respectivamente Lo anterior fija la geometría de los clusters. La actualización de U se logra mediante (14). El proceso concluye cuando la diferencia entre U actual y U anterior es menor que el limite de tolerancia ε (0.01 ó 0.001).
Este algoritmo tiene la ventaja de ser prácticamente insensible a los parámetros de inicialización. Presenta limitaciones en cuanto al volumen de los cluster debido a la restricción en (9) incapacitándolo para identificar clusters con diferentes volúmenes. Además, si el sistema presenta linealidades o la cantidad de datos es muy pequeña, Ai puede presentar problemas de singularidad, interrumpiendo el proceso iterativo. En [5] se presentan dos técnicas para corregir los problemas matemáticos que pueden surgir en el cálculo de la matriz de covarianza Ai.
B. ALGORITMO MAXIMUM LIKELIHOOD ESTIMATION (MLE)
El concepto de likelihood está cercanamente relacionado con el de probabilidad [5][7][4]. En la teoría de probabilidad clásica se intenta predecir la probabilidad de que cierto dato o evento ocurra, de acuerdo a parámetros de una función de densidad de probabilidad (pdf) dada. El objetivo de MLE es encontrar los valores de los parámetros que maximicen el valor una pdf establecida a partir de los datos o eventos obtenidos.
Sin embargo, es más sencillo obtener los parámetros de la pdf a partir de la maximización del logaritmo natural de dicha función, esta técnica se conoce como log likelihood [7]. La pdf de la cual se obtiene los parámetros es una combinación lineal o suma de pdf s normales multivariables y cada una de estas representa un cluster.
Una función de densidad de probabilidad normal multivariable tiene la siguiente forma [4][7]:
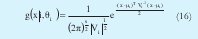
La cual se entiende como la probabilidad que suceda el evento x dados los parámetros θi, estos son la iésima matriz de covarianza Vi y la i-ésima media µi (elemento prototipo del i-ésimo cluster). s es la dimensión de los datos, por tanto las dimensión de la matriz de covarianza es (s x s) y la de la media es s.
Al realizar una mezcla de pdf s normales la pdf resultante es de la forma:
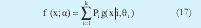
Que indica la suma de pdf's normales con coeficientes Pi. Ahora los parámetros de la función se conocen como α y son Vi, µi y Pi. Si se toma a Pi como la probabilidad a priori de seleccionar la iésima función, es decir, de seleccionar el i-ésimo cluster, se debe cumplir de acuerdo a la teoría clásica de probabilidad que:

Suponiendo N eventos (datos) se desea encontrar una pdf que haga más probable a todos los eventos, es decir, más probable el evento 1 "y" el eventeo2 "y" el evento N. La pdf resultante estará dada por:

Observe que esta pdf tiene exactamente los mismos parámetros que f(xk,α). Ahora el logaritmo de H es: Al
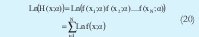
AL aplicar MLE a esta función se buscan los parámetros α que maximicen Ln (H(x;a)), bajo la condición (18). Debido a esto se aplican multiplicadores de Lagrange para llegar a las siguientes expresiones:
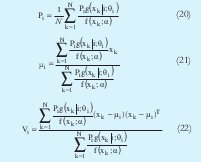
Ahora aplicando la regla de Bayes [8] se obtiene:
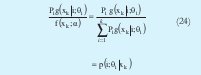
Entonces se puede rescribir de la siguiente forma el algoritmo:
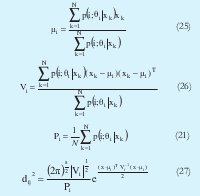
Al igual que en GK, (27) describe la ecuación de elipses rotadas que determina la geometría del cluster. Sin embargo, este algoritmo no tiene restricciones en cuanto al volumen de cada cluster. El proceso de actualización de los parámetros y convergencia del proceso es similar al utilizado en GK. Una de las desventajas que presenta este algoritmo es que debido a su distancia exponencial es sensible a los parámetros de inicialización.
C. VERSIÓN DE EJES PARALELOS SIMPLIFI CADA DEL MAXIMUM LIKELIHOOD ESTIMATION
Como ya se dijo el algoritmo MLE tiene como una de las variables a minimizar la matriz de covarianza. Esto produce clusters rotados de forma hiperelipsoidal, de acuerdo a la orientación de cada subgrupo.
En la versión de ejes paralelos simplificada la matriz de covarianza se toma como una matriz diagonal[9][10]. Cada uno de los elementos de la matriz es la desviación estándar de cada una de las variables en cada cluster[9]. Con este nuevo planteamiento cada una de las pdf's g(x |i, θi) ,que compone la mezcla se puede rescribir como:
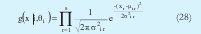
donde x es el vector que representa un dato tomado, s la dimensión de cada dato, xr representa la r-ésima componente del vector x, µi r es r-ésima componente del centro del i-ésimo cluster µi y σ2i r representa la desviación estándar de la r-ésima variable en el i-ésimo cluster. Siguiendo un procedimiento similar al descrito para obtener el algoritmo del MLE se llega a:
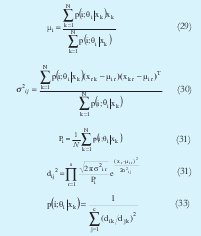
Debido a que la matriz es diagonal, solo se obtendrán clusters de forma elipsoidal pero paralelos a cada uno de los ejes del espacio muestreal. Obsérvese que teniendo en cuenta la ecuación (28), la funciona objetivo de la ecuación (17) se puede rescribir como:
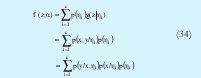
En este caso cada dato es representado por un vector z y es dividido en un vector de entrada x y una constante de salida y. A p(xk/ηi) se le denomina distribución de entrada y es de la forma:
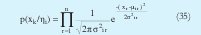
donde n es la dimensión de entrada y p(y/x, çi) se le denomina distribución de salida y es de la forma:
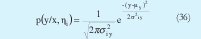
D. MODIFICACIÓN DE LA VERSIÓN SIMPLIFICADA DEL MLE
Esta modificación se basa en interpretación dada por las ecuaciones (34), (35) y (36) a la versión simplificada del MLE y busca mejorar la interpretación a la hora de derivar modelos TSK. Esta variación plantea una distribución de entrada de la forma de la ecuación (35), y una distribución de salida en la que a la vez se evalúa un modelo lineal de la salida como función de las variables de entrada [9][10].
En esta técnica las distribuciones de entrada y salida están determinadas por:

Donde θi indica los parámetros del i-ésimo modelo lineal de salida. También se presenta la siguiente restricción:
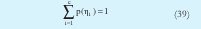
Siendo p(ηi) la probabilidad a priori de cada cluster. Utilizando un proceso similar al desarrollado para obtener el algoritmo MLE se llega a las siguientes expresiones que genera el proceso iterativo.
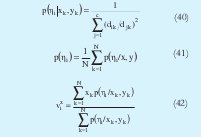
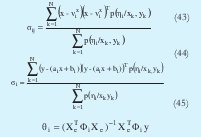
Xe denota una matriz de regresión extendida, la cual se forma de la siguiente manera: primero que todo se forma una matriz llamada X, donde a cada fila le corresponde el valor de las componentes de entrada de cada uno de los datos. Después se adiciona una columna de unos obteniendo Xe, es decir Xe=[X 1] y Φi denota una matriz diagonal que contiene las funciones de pertenencia de cada dato al iésimo cluster.
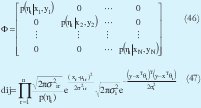
El proceso de actualización de los parámetros y convergencia del algoritmo es similar a GK y se utiliza (40) para la reconstrucción de U. Al igual que MLE este algoritmo presenta problemas de inicialización.
V. DERIVACIÓN DE MODELOS TSK A PARTIR DE LOS PARAMETROS OBTENIDOS EN LOS METODOS DE CLUSTERING
El problema de derivar los modelos TSK se reduce a hallar los parámetros de la función lineal en los consecuentes y las funciones de pertenencia en los antecedentes. Se debe tener en cuenta que el método modificado de la versión simplificada del MLE brinda ya todos los parámetros de los consecuentes. Por tanto solo se describirán métodos para derivar consecuentes a partir de las particiones y parámetros obtenidos en los métodos de clustering GK y MLE
A. DERIVACIÓN DE CONSECUENTES
Para derivar los consecuentes los dos métodos usados más comúnmente son: mínimos cuadrados totales y mínimos cuadrados ponderados [4]:
Mínimos cuadrados totales (TLS): Como resultado de las técnicas de clustering se obtienen clusters de forma hiperelipsoidal que pretenden aproximar hiperplanos, por tanto el eje más pequeño del hiperelipse debe tender a ser perpendicular al hiperplano que se quiere aproximar. Las direcciones y las magnitudes de los ejes de los hiperelipses están determinadas por los autovectores y los autovalores de cada matriz de covarianza respectivamente. El autovalor más pequeño indica cual de los ejes del hiperelipse es más pequeño y por tanto indica que el correspondiente autovector es perpendicular al hiperplano. Basándose en esta idea y teniendo en cuenta que el hiperplano debe pasar por cierto punto con determinadas coordenadas llamado centro se construye la ecuación de un hiperplano:
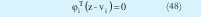
Donde φiT es el autovector correspondiente al autovalor más pequeño de la i-ésima matriz de covarianza y vi es el i-ésimo centro. Ahora el autovector φi y el centro vi se pueden rescribir partiéndolos en sus dimensiones de la siguiente forma:
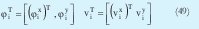
Donde (φix)T y (vix)T son la parte de los vectores φiT y viT respectivamente que corresponden a las variables de entrada mientras que φiy y viy son las constantes que corresponden a la salida Teniendo en cuenta esto la ecuación (44) se puede rescribir de la siguiente forma.
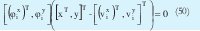
Lo que conduce a:
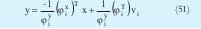
Donde
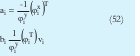
que son los consecuentes de la i-ésima regla. Esta solución es basada en la interpretación geométrica de los cluster, pero también esta demostrado [4] que es la solución al sistema:
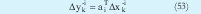
Mínimos cuadrados ponderados (WLS): Este métodos plantea minimizar los errores de predicción de los modelos locales individuales, resolviendo como un conjunto de c independientes problemas (uno para cada cluster) de mínimos cuadrados ponderados. Lo anterior se obtiene a partir de la minimización del siguiente criterio:
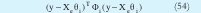
donde Xe es la misma matriz que se describió en la sección IV. Como resultado se obtiene la ecuación (45), es decir:
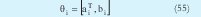
Es conveniente utilizar TLS en lugar de WLS, en datos donde se considere que existe ruido, ya que TLS brinda de cierta forma robustez frente al ruido. También es importante resaltar que en la modificación a la versión simplificada de MLE en cada iteración del algoritmo se esta usando WLS, por tanto el propio algoritmo brinda los consecuentes sin necesidad de procedimientos extra.
B. DERIVACIÓN DE ANTECEDENTES
Como resultado del clustering se obtienen funciones de pertenencia multivariable. Es difícil la interpretación e implementación multidimensional de conjuntos difusos, por lo tanto los antecedentes en (1) deben ser reescritos como una combinación de proposiciones simples con conjuntos difusos unidimensionales. Para este fin se pueden aplicar dos estrategias: proyección ortogonal y proyección autovector [4].
Proyección Ortogonal: Proyecta la función de pertenencia multivariable sobre cada uno de los ejes correspondientes a las diferentes variables de entrada de la siguiente forma:
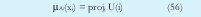
Esta proyección presenta errores ya que los clusters no siempre están paralelos a los ejes y se produce el denominado error por proyección.
Proyección con autovector: Ya se describió como los autovectores indican la dirección de los ejes rotados de las hyperelipses, por tanto se puede utilizar esta propiedad para formar una matriz de rotación y luego proyectar ortogonalmente. Esta solución aunque más precisa, tiene el problema que es poco interpretable, ya las nuevas entradas se convierten en combinaciones lineales de la entradas originales (por el proceso de rotación de ejes a través de la matriz).
Una vez obtenidas las funciones de pertenencia univariables por cualquiera de los dos métodos de proyección, se deben usar una curva parametrizada que aproxime lo mejor posible el punto proyectado.
VI. SIMULACIONES Y RESULTADOS
En esta sección son desarrollados 3 ejemplos para verificar la robustez y exactitud en la generación de modelos. Para la generación de antecedentes se implementó la proyección ortogonal descrita en la sección V.B.. En cuanto a los parámetros de los consecuentes fueron derivados a partir del método TLS para los algoritmos GK y MLE. WLS fue implementado para la modificación de MLE simplificado. En el primer ejemplo de aplicación se tomó una función compuesta de dos funciones lineales, descrita de la siguiente forma:

Fue agregado ruido gaussiano con media 0 y desviación estándar de 0.2, N(0, σ2). Se tomaron 1000 muestras por cada submodelo, es decir 2000 muestras en total. Los funciones de pertenencia obtenidas para los antecedentes son mostrados en las figura 1. La función, los datos con ruido agregado y los consecuentes obtenidos son mostrados en la figura 2 Además los parámetros encontrados para los consecuentes son tabulados en la tabla 1.
Se puede observar en la Fig.1(a) que la frontera (punto en el cual el valor de la función de pertenencia es 0.5) originada por el algoritmo GK entre ambos clusters esta alrededor de 1,2. Idealmente esta frontera se debería encontrar en 1, tal como lo sugiere la ecuación (57). Este desplazamiento es debido a la presencia de ruido, sin embargo, es una buena aproximación. Los mejores resultados se obtuvieron cuando se empleó el algoritmo MLE donde la frontera se encuentra cercana a 1.1 lo cual significa que agrupó la dispersión de manera más eficiente, tal como se ve en la Fig. 1(b). El peor resultado es obtenido al utilizar la modificación de MLE ya que la frontera se presenta de 0.75, además de esto las proyecciones que representan las funciones de pertenencia son las más dispersas como se observa en la Fig.1(c).
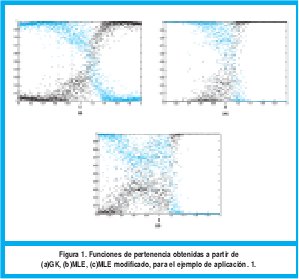
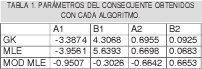
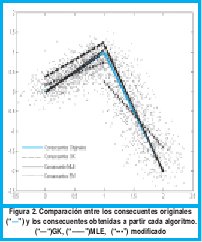
Comparando las graficas 2(a) y 2(b), se puede evidenciar mejor el hecho que el algoritmo GK tiende a generar clusters de igual volumen, ya que los parámetros del primer submodelo fueron bastante próximos a los ideales, mientras que los del segundo son apenas buenos. Los parámetros obtenidos con el algoritmo MLE son bastantes buenos para ambos clusters. Observando la grafica 2(c) se confirma el hecho evidenciado en la Fig. 1(c), donde se observa que la modificación del algoritmo MLE no identifica bien los submodelos lineales, ya que los consecuentes hallados a través de esta modificación se encuentran lejanos a los originales.
En el segundo ejemplo se toma una función compuesta idéntica a la del ejemplo 1, variando la desviación estándar a 0. Los funciones de pertenencia obtenidas para los antecedentes y son mostrados en las figura 3. La función, los datos con ruido agregado y los consecuentes obtenidos son mostrados en la figura 4 Además los parámetros encontrados para los consecuentes son tabulados en la tabla 2.
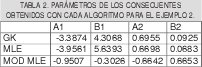
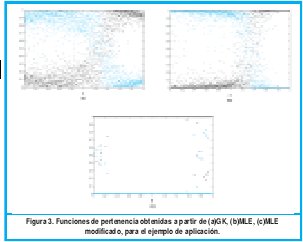
De la Fig.3(a) y 3(b) se puede observar que los puntos de frontera se colocan aproximadamente en 1.3 para las funciones de pertenencia obtenidas a partir de los algoritmos GK y MLE. La diferencia radica que con GK se derivan conjuntos más difusos, mientras MLE tienden a generar conjuntos concretos (no difusos). El error en el punto de frontera de nuevo se debe al ruido que en este caso es mayor que en el ejemplo 1. Los resultados obtenidos con la modificación del MLE son pésimos. El algoritmo identificó la partición como un solo cluster, ya que, para uno de los conjuntos, el valor de la función de pertenencia es uno en todo el rango de la variable de entrada, mientras que en el otro conjunto cero, tal como se ve en la Fig. 3.(c).
Al observar la Fig. 4 y la tabla 2 se puede concluir que el algoritmo que mantiene un aceptable desempeño para derivar consecuentes es el algoritmo GK.
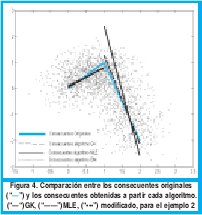
Con el MLE no se derivan consecuentes aproximados a los reales para ninguno de los dos clusters, su desempeño es pobre en comparación con el obtenido en GK. Confirmando así los resultados obtenidos en las funciones de pertenencia. A partir de la Fig. 4. (c) se puede observar que el MLE modificado presenta un pésimo desempeño a la hora de obtener consecuentes representativos de la dispersión de datos. En el tercer ejemplo se tomó una función no lineal descrita en la siguiente ecuación:
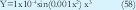
A dicha función le fue agregado ruido gaussiano N(0,σ2) con media 0 y desviación estándar de 5. Se tomaron 200 muestras en total. Los resultados obtenidos son mostrados en las graficas 5, 6 y 7.
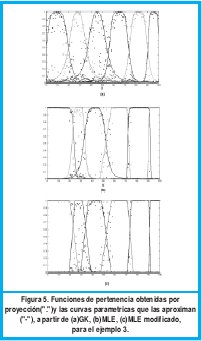
En la figura 5 se puede observar que los 3 algoritmos pueden identificar bastante bien los subgrupos dentro de la dispersión de datos. En el algoritmo GK se presenta conjuntos difusos con transiciones suaves mientras que las transiciones obtenidas con los algoritmos MLE y MLE modificados son bastante abruptas.
En la Fig. 6 se muestran los submodelos lineales obtenidos a partir de cada algoritmo de clustering. Nótese que el algoritmo GK no identifica muy bien los dos primeros cluster mientras MLE y su modificación no identifican muy bien el segundo cluster.
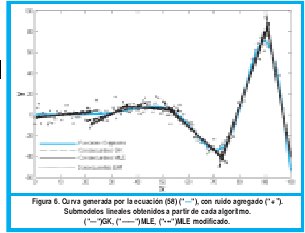
En la figura 7 se muestra la salida que produce cada uno de los modelos. Para poder evaluar cuantitativamente el desempeño del modelo, fue aplicado el criterio RMSE, el cual es definido así:
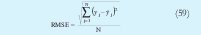
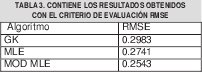
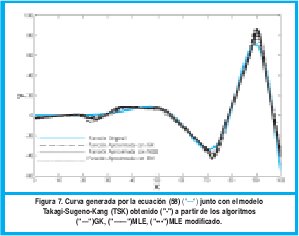
El algoritmo que obtuvo el peor desempeño fue el GK, confirmando el hecho analizado con la figura 6, donde GK fue el algoritmo que no identifico apropiadamente dos de los submodelos lineales. En este caso el que obtuvo un mejor desempeño fue el MLE modificado, porque logro identificar submodelos lineales más cercanos al comportamiento real.
VII. CONCLUSIONES
Las técnicas de clustering son una excelente herramienta para derivar modelos difusos tipo TSK capaces de aproximar sistemas no lineales.
Observando los ejemplos 1 y 2 se puede concluir que el algoritmo más robusto frente al ruido es GK. Por el contrario el más sensible ante el ruido es MLE modificado. Sin embargo en condiciones de poco ruido el algoritmo MLE modificado puede identificar mejor submodelos lineales que sean más próximos al modelo general.
Para trabajos futuros se puede pensar en aplicar técnicas de clustering robusto a los algoritmos con el fin de volverlos menos insensibles ante la presencia de ruido.
REFERENCIAS BIBLIOGRÁFICAS
[1] L.X.Wang, A Course in Fuzzy Systems and Control. Prentice Hall, 1997.
[2] T. Takagi and M. Sugeno, "Fuzzy Identification of Systems and Its Applications to Modeling and Control", IEEE Trans.on Systems, Man and Cybernetics, vol. SMC-15, No.1, 1985
[3] D. E. Gustafson and W. C. Kessel, "Fuzzy Clustering with a Fuzzy Covariance", Proc.IEEE CDC, pp 761-766, San Diego, CA, USA, 1979
[4] R. Babuska, Fuzzy Modeling for Control. Kluwer Academic Publishers, 1998.
[5] R. Babuska, "et al", "Improved Covariance Estimation for Gustafson-Kessel Clustering", Proc. Of the 2002 IEEE International Conference on Fuzzy Systems,vol. 2, pp. 1081-1085, 2002.
[5] I. Gath and A. B. Geva, "Unsupervised Optimal Fuzzy Clustering", IEEE Trans. On Pattern Analisis and Machine Intelligence, vol. 11, No. 7, pp. 773-781, 1989.
[7] J. C. Bezdek and J. C. Dunn, "Optimal Fuzzy Partitions": A Heuristic for Estimating the Parameters in a Mixture of Normal Distributions", IEEE Trans.on Computers, pp. 835-838, 1975
[8] P. L. Meyer, Probabilidad y Aplicaciones Estadisticas, Addison Wesley, 1992.
[9] J. Abonyi, "et al", "Modified Gath-Geva Fuzzy Clustering for Identification of Takagi-Sugeno Fuzzy Models", IEEE Trans. on Systems, Man and Cybernetic, Part B, October, 2002.
[10] J. Abonyi, "et al", "Identification of Nonlinear System Using Gaussian Mixture of local Models", Hungarian Journal of Industrial Chemestry, vol. 29, 134-139, 2001.
Diana Marcela González Chaparro
Miembro del Grupo de investigación: Laboratorio de Automática, Microelectrónica e Inteligencia Computacional LAMIC.
Sergio Barato Quintero
Miembro del Grupo de investigación: Laboratorio de Automática, Microelectrónica e Inteligencia Computacional LAMIC.
Creation date:
License
From the edition of the V23N3 of year 2018 forward, the Creative Commons License "Attribution-Non-Commercial - No Derivative Works " is changed to the following:
Attribution - Non-Commercial - Share the same: this license allows others to distribute, remix, retouch, and create from your work in a non-commercial way, as long as they give you credit and license their new creations under the same conditions.





2.jpg)










