DOI:
https://doi.org/10.14483/udistrital.jour.reving.2016.2.a02Publicado:
2016-05-26Número:
Vol. 21 Núm. 2 (2016): Mayo - AgostoSección:
Inteligencia ComputacionalNie-Tan Method and its Improved Version: A Counterexample
Palabras clave:
Type-2 fuzzy logic system, type-2fuzzy set, centroid, defuzzification, Nie-Tanmethod. (en).Descargas
Referencias
J. M. Mendel and R. I. John, “Type-2 fuzzy sets made simple,” IEEE Transactions on Fuzzy Systems, vol. 10, no. 2, pp. 117–127, 2002.
O. Castillo and P. Melin, Type-2 Fuzzy Logic: Theory and Applications, ser. Studies in Fuzziness and Soft Computing. Springer-Verlag Berlin Heidelberg, 2008, vol. 223.
N. N. Karnik and J. M. Mendel, “Type-2 fuzzy logic systems : Type-reduction,” in IEEE International Conference on Systems, Man, and Cybernetics, vol. 2, San Diego, California, USA, Oct. 1998, pp. 2046–2051.
J. M. Mendel, R. I. John, and F. Liu, “Interval type-2 fuzzy logic systems made simple,” IEEE Transactions on Fuzzy Systems, vol. 4, no. 6, pp. 808–821, Dec. 2006.
O. Salazar, J. Soriano, and H. Serrano, “Centroid of an interval type-2 fuzzy set: Continuous vs. discrete,” Ingeniería, vol. 16, no. 2, pp. 67–78, 2011, ISSN 0121-750X.
N. N. Karnik, J. M. Mendel, and Q. Liang, “Type-2 fuzzy logic systems,” IEEE Transactions On Fuzzy Systems, vol. 7, no. 6, pp. 643–658, 1999.
N. N. Karnik and J. M. Mendel, “Centroid of a type-2 fuzzy set,” Information Sciences, vol. 132, pp. 195–220, 2001.
S. Coupland and R. John, “An investigation into alternative methods for the defuzzification of an interval type-2 fuzzy set,” in Proceedings of the 2006 IEEE International Conference on Fuzzy Systems, Vancouver, Canada, Jul. 2006, pp. 1425–1432.
J. M. Mendel, “Type-2 fuzzy sets and systems: An overview,” IEEE Computational Intelligence Magazine, vol. 2, no. 1, pp. 20–29, Feb. 2007.
J. Aisbett, J. T. Rickard, and D. G. Morgenthaler, “Type-2 fuzzy sets as functions on spaces,” IEEE Transactions on Fuzzy Systems, vol. 18, no. 4, pp. 841–844, Aug. 2010.
J.M.Mendel and X. Liu, “New closed-form solutions for karnik-mendel algorithm+defuzzification of an interval type-2 fuzzy set,” in Proceedings of the 2012 IEEE International Conference on Fuzzy Systems (FUZZ-IEEE), Brisbane, QLD, Jun. 2012, pp. 1–8.
——, “Simplified interval type-2 fuzzy logic systems,” IEEE Transactions on Fuzzy Systems, vol. 21, no. 6, pp. 1056–1069, 2013.
M. Nie and W. W. Tan, “Towards an efficient type-reduction method for interval type-2 fuzzy logic systems,” in Proceedings of the IEEE International Conference on Fuzzy Systems (FUZZ 2008), 2008, pp. 1425–1432.
S. Greenfield and F. Chiclana, “Accuracy and complexity evaluation of defuzzification strategies for the discretized interval type-2 fuzzy set,” International Journal of Approximate Reasoning, vol. 54, pp. 1013–1033, 2013.
J. M. Mendel, Uncertainty Rule-Based Fuzzy Logic Systems: Introduction and New Directions. Prentice-Hall PTR, 2001.
D. Wu and M. Nie, “Comparison and practical implementation of type-reduction algorithms for type-2 fuzzy sets and systems,” in Proceedings of the IEEE International Conference on Fuzzy Systems (FUZZ 2011), 2011, pp. 2131–2138.
J.M.Mendel and H.Wu, “Uncertainty bounds and their use in the design of interval type-2 fuzzy logic systems,”IEEE Transactions on Fuzzy Systems, vol. 10, no. 5, pp. 622–639, 2002.
S. Greenfield, F. Chiclana, S. Coupland, and R. John, “The collapsing method of defuzzification for discretized interval type-2 fuzzy sets,” Information Sciences, vol. 179, no. 13, pp. 2055–2069, 2009.
J. M. Mendel and H. Wu, “Properties of the centroid of an interval type-2 fuzzy set, including the centroid of a fuzzy granule,” in Proceedings of the 2005 International Conference on Fuzzy Systems (FUZZ-IEEE 2005), 2005, pp. 341–346.
——, “New results about the centroid of an interval type-2 fuzzy set, including the centroid of a fuzzy granule,” Information Sciences, vol. 177, pp. 360–377, 2007.
O. Salazar and J. Soriano, “Generating embedded type-1 fuzzy sets by means of convex combination,” in Proceedings of the 2013 IFSA World Congress NAFIPS Annual Meeting, Edmonton, Canada, Jun. 2013, pp. 51–56.
——, “Convex combination and its application to fuzzy sets and interval-valued fuzzy sets I,” Applied Mathematical Sciences, vol. 9, no. 22, pp. 1061–1068, 2015, ISSN 1312-885X.
——, “Convex combination and its application to fuzzy sets and interval-valued fuzzy sets II,” Applied Mathematical Sciences, vol. 9, no. 22, pp. 1069–1076, 2015, ISSN 1312-885X.
J. M. Mendel and F. Liu, “Super-exponential convergence of the Karnik-Mendel algorithms for computing the centroid of an interval type-2 fuzzy set,” IEEE Transactions on Fuzzy Systems, vol. 15, no. 2, pp. 309–320, Apr. 2007.
X. Liu and J. M. Mendel, “Connect karnik-mendel algorithms to root-finding for computing the centroid of an interval type-2 fuzzy set,” IEEE Transactions on Fuzzy Systems, vol. 19, no. 4, pp. 652–665, 2011.
Cómo citar
APA
ACM
ACS
ABNT
Chicago
Harvard
IEEE
MLA
Turabian
Vancouver
Descargar cita
DOI: http://dx.doi.org/10.14483/udistrital.jour.reving.2016.2.a02
Nie-Tan Method and its Improved Version: A Counterexample
Método Nie-Tan y su Versión Mejorada: Un contraejemplo
Juan D. Rojas
Universidad Distrital Francisco José de Caldas.
Omar Salazar
Universidad Distrital Francisco José de Caldas. osalazarm@correo.udistrital.edu.co
Humberto Serrano
Universidad Distrital Francisco José de Caldas.
Received: 13-10-2016. Modified: 18-01-2016. Accepted: 30-03-2016
Abstract
Context: The bottleneck on interval type-2 fuzzy logic systems is the output processing when using Centroid Type-Reduction + Defuzzification (CTR+D method). Nie and Tan proposed an approximation to CTR+D (NT method). Recently, Mendel and Liu improved the NT method (INT method). Numerical examples (due to Mendel and Liu) exhibit the NT and INT methods as good approximations to CTR+D.
Method: Normalization to the unit interval of membership function domains (examples and counterexample) and variables involved in the calculations for the three methods. Examples (due to Mendel and Liu) taken from the literature. Counterexample with piecewise linear membership functions. Comparison by means of error and percentage relative error.
Results: NT vs. CTR+D: Our counterexample showed an error of 0:1014 and a percentage relative error of 30:53%. This is respectively 23 and 32 times higher than the worst case obtained in the examples. INT vs. CTR+D: Our counterexample showed an error of 0:0725 and a percentage relative error of 21:83%. This is respectively 363 and 546 times higher than the worst case obtained in the examples.
Conclusions: NT and INT methods are not necessarily good approximations to the CTR+D method.
Keywords: Type-2 fuzzy logic system, type-reduction, defuzzification, Nie-Tan method.
Language: English.
Resumen
Contexto: El cuello de botella en sistemas de lógica difusa tipo-2 de intervalo es el procesamiento de salida que usa reducción de tipo centroide + defusificación (método CTR+D). Nie y Tan propusieron una aproximación a CTR+D (método NT). Recientemente, Mendel y Liu mejoraron la propuesta (método INT). Ejemplos debidos a Mendel y Liu exhiben a NT e INT como buenas aproximaciones a CTR+D.
Método: Normalización al intervalo unitario de los dominios de las funciones de pertenencia (para ejemplos y contraejemplo) y de las variables que intervienen en los cálculos de los tres métodos. Ejemplos tomados de la literatura (debidos a Mendel y Liu). Contraejemplo con funciones de pertenencia lineales por tramos. Comparación por medio de métricas de error y porcentaje de error relativo.
Resultados: NT vs. CTR+D: El contraejemplo mostró un error de 0.1014 y error relativo porcentual de 30.53%. Esto es respectivamente 23 y 32 veces mayor que el peor caso obtenido en los ejemplos. INT vs. CTR+D: El contraejemplo mostró un error de 0.0725 y error relativo porcentual de 21:83%. Esto es respectivamente 363 y 546 veces mayor que el peor caso obtenido en los ejemplos.
Conclusiones: NT e INT no son necesariamente buenas aproximaciones al método CTR+D.
Palabras clave: Sistema de lógica difusa tipo-2, reducción de tipo, defusificación, método Nie-Tan.
1. Introduction
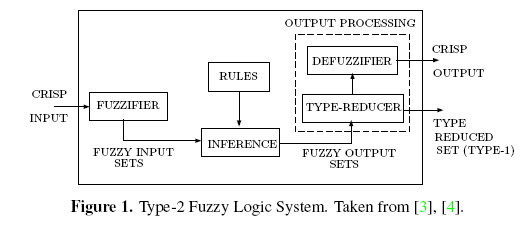
Type-2 Fuzzy Logic Systems (T2FLS) (Figure 1) are used in several applications because Type-2 Fuzzy Sets (T2FS) provide greater flexibility than Type-1 Fuzzy Sets (T1FS) [1], [2]. In a T2FLS a crisp numerical input goes through three stages: fuzzification, inferencing, and the output processing. During the output processing a T2FS is converted into a crisp number. This last stage consists of two parts: type-reduction and defuzzification. Type-reduction is the procedure by which a T2FS is converted to a T1FS (called the type-reduced set). This set is then defuzzified to give a crisp number.
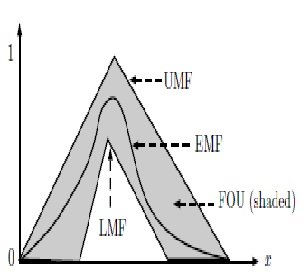
In order to facilitate operations on T2FLSs, Interval Type-2 Fuzzy Sets (IT2FS) were introduced (Figure 2). IT2FSs are a simplified version of general T2FSs. IT2FSs are defined by two membership functions (MF): the Lower Membership Function (LMF) and the Upper Membership Function (UMF). Any MF between LMF and UMF is called an Embedded Membership Function (EMF). The region bounded by LMF and UMF is called Footprint of Uncertainty (FOU). The corresponding FLSs are called Interval Type-2 Fuzzy Logic Systems (IT2FLS) [4].
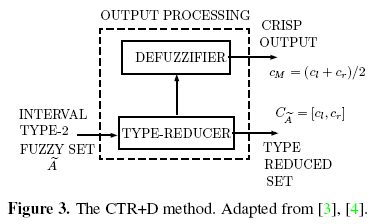
Since IT2FLSs were proposed, centroid type-reduction 1 (Figure 3) has been one of the main areas of study, mainly due to its high computational cost [3], [6]-[9]. If à is an IT2FS, the main problem consists in finding the type-reduced set2 CÃ= [cl; cr], where cl and cr are the endpoints of CÃ. The interval [cl; cr] contains the centroids of all EMFs in the FOU. Defuzzification, which consists in averaging cl and cr to get cM = (cl +cr)/2, is a relatively simple step in IT2FLSs. Figure 3 is what we shall refer to as the Centroid Type-Reduction + Defuzzification (CTR+D) method 3.
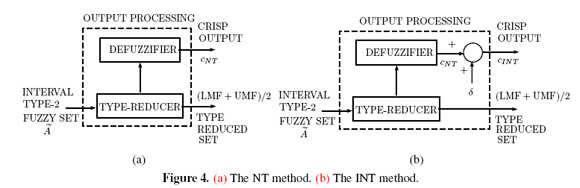
Nie and Tan [13] proposed an approximation to the CTR+D method. It is known as the Nie-Tan(NT) method. It consists in averaging LMF and UMF to get an average MF (AMF). The defuzzified value cNT is the centroid of this AMF (Figure 4(a)). Mendel and Liu [11], [12] improved the NT method. Their improvement is still an approximation. It is known as the Improved Nie-Tan (INT) method. It consists in adding to cNT a correction factor δ, i.e., cINT = cNT + δ (Figure 4(b)).
Mendel and Liu showed four numerical examples in order to illustrate their theoretical results. These authors claimed that cNT is a first-order approximation to cM = (cl +cr)/2, and cINT is a better third-order approximation to cM. Their examples included IT2FSs defined over different domains, and they used the following metrics for comparison:
1. Absolute error: 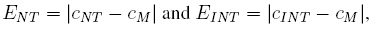
2. Percentage relative error: 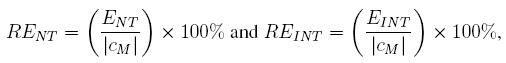
3. Difference of absolute errors: 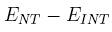 ,and
,and
4. Absolute error ratio: 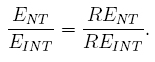
Their numerical results showed 0 ≤ ENT ≤ 0.0844, 0 ≤ EINT ≤ 0.0014, 0% ≤ REINT ≤ 2.22%, and 0% ≤ REINT ≤ 0.04%. In terms of error comparison, their results showed 0 ≤ ENT - EINT ≤ 0.0829 and 4.29 ≤ ENT/EINT ≤ 58.93. Although these results seem to exhibit the NT and INT methods as a good approximation to the CTR+D method, in this paper we will show this is not necessarily true.
The metrics shown above depend on two things: (1) the domain where LMF and UMF are defined and (2) the images of these two MFs. Let us explain this point in general terms. Let à be an IT2FS defined over a domain X. If μ Ae : X → [0; 1] : x → μ Ae (x) is an EMF then its centroid is given by
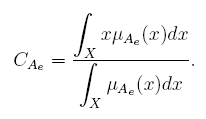
Therefore, CAe depends on two things for its calculation: (1) the domain X and (2) the image4 of μ Ae , denoted as Im(μ Ae). As a consequence, if M is a metric calculated from CAe1 and CAe2 (centroids of two EMFs), M depends on X, Im(μ Ae1) and Im(μ Ae2). As we will see in next sections: c M, cNT and cINT are calculated from X, LMF and UMF (two particular EMFs). Therefore, ENT , EINT , RENT , REINT , ENT - EINT, and ENT / EINT = RENT/REINT depend on the domain where LMF and UMF are defined and the images of these two MFs.
The aim of this paper is to show a counterexample that exhibits higher errors than the corresponding errors in examples reported in the literature when comparing CTR+D method versus NT and INT methods5. We chose an IT2FS with piecewise linear MFs, mainly due to its simplicity. In order to reduce the effect of different domains on the metrics (as we explained above), all the domains (for examples and counterexample) were taken to a common domain: the unit interval [0; 1]. This has a consequence: a change on a metric is due mainly to the change in the LMFs and UMFs (the shape of the FOU). Additionally, all the variables involved in the CTR+D, NT and INT methods were normalized to the unit interval.
After normalizing Mendel and Liu's results, their four numerical examples showed 0 ≤ E*NT ≤ 0.0044, 0 ≤ E*INT≤ 0.0002, 0% ≤ RE*NT≤ 0:96%, and 0% ≤ RE*INT≤ 0:04%. In terms of error comparison, their examples showed 0 ≤ ENT -EIN≤ 0.0044 and 4:42 ≤ ENT=EINT ≤ 60.21. Our counterexample showed E*NT = 0.1014 (23 times higher than E*NT = 0.0044), E*INT = 0.0725 (363 times higher than E*INT = 0.0002), RE*NT = 30:53% (32 times higher than RE*NT = 0.96%), and RE*INT = 21:83% (546 times higher than RE*INT = 0.04%). In terms of error comparison, our counterexample showed E*NT -E*INT = 0.0289 and E*NT=E*INT = 1.3986. We concluded, based on our results, that the NT and INT methods are not necessarily good approximations to the CTR+D method.
This paper is organized as follows: In Section 2 some preliminaries related to the CTR+D, NT and INT methods are presented. In Section 3, our normalization to the unit interval is described.In Section 4, the main results are shown. Finally, discussion and conclusions are presented in Section 5 and Section 6.
2. Preliminaries
Let à be an IT2FS, which is determined by two MFs6 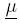 : X → [0; 1] and
: X → [0; 1] and 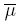 : X → [0; 1], defined over a nonempty set X ⊂ ℝ, such that(x) ≤ (x) for all x ∈ X. μ is called Lower Membership
Function (LMF) and
: X → [0; 1], defined over a nonempty set X ⊂ ℝ, such that(x) ≤ (x) for all x ∈ X. μ is called Lower Membership
Function (LMF) and 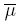 is called Upper Membership Function (UMF). In many applications X is a closed interval7, therefore from now on we will suppose X = [a, b] ⊂ ℝ, with a < b. The centroid (type-reduced set) of Ã, denoted by CÃ , is CÃ = [cl, cr] ⊆ X, where cl and cr are
is called Upper Membership Function (UMF). In many applications X is a closed interval7, therefore from now on we will suppose X = [a, b] ⊂ ℝ, with a < b. The centroid (type-reduced set) of Ã, denoted by CÃ , is CÃ = [cl, cr] ⊆ X, where cl and cr are
and where θ : X → [0, 1] is a MF such that
for all x ∈ X. The defuzzified value of à is
It was shown [19], [20] that the θ functions to minimize and maximize (1) are respectively
where xl, xr ∈ X are unknown (a priori) switch points between 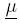 and
and 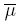 . The switch points xl and xr need to be found by means of iterative procedures in order to optimize (1).
. The switch points xl and xr need to be found by means of iterative procedures in order to optimize (1).
Convex combination [21]-[23] was used to characterize all the θ functions that satisfy (2). It is known that for any θ which satisfies (2), there is at least one MF μΛ: X → [0, 1] such that
for all x ∈ X. If μΛ is taken in (5) as
then (4) is achieved. Therefore, cl = min t ∈ X α(t) and cr = maxt ∈ X α(t), where
for all x ∈ X
It was also shown [19], [20], [24] that α (cl) = cl and (cr) = cr (cl and cr are fixed points of α and β), i.e.,
From (8) it was shown [11], [12], [25] that the problem of finding cl and cr is equivalent to find the roots in [a, b] of
which are defined for all t ∈ X, and where φ(cl) = 0 and ω(cr) = 0. It was also shown [25] that the Karnik-Mendel algorithm is equivalent to applying the Newton-Raphson method to find the roots of φ and ω.
In the Nie and Tan's original method [13], the MF obtained after type-reducing is the average of
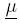 and
and 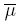 , i.e., μ NT (x) = (μ(x) + μ(x))/2 for all x ∈ X. Therefore, its defuzzified value is
, i.e., μ NT (x) = (μ(x) + μ(x))/2 for all x ∈ X. Therefore, its defuzzified value is
Mendel and Liu [11], [12] claimed that cNT is a first-order approximation to cM = (cl + cr ) / 2.
Mendel and Liu [11], [12] proposed the improved Nie-Tan method, which is
where cNT is given in Section 2.2, and δ is given by
These authors claimed that cINT is a better third-order approximation to cM = (cl + cr ) / 2
3. Normalization to the unit interval
Since the domain of 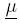 and
and 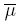 is X = [a; b], with a < b, a bijective function is established [a; b] → [0; 1] : x → y which is given by
is X = [a; b], with a < b, a bijective function is established [a; b] → [0; 1] : x → y which is given by
Its inverse function [0, 1] → [a, b] : y → x (also a bijection) is given by
By means of (15) we define MFs with normalized domain (to the unit interval) 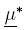 : [0, 1] → [0; 1]
and
: [0, 1] → [0; 1]
and 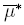 : [0, 1] → [0, 1] given by
: [0, 1] → [0, 1] given by
for all y ∈ [0; 1], and where 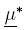 (y) ≤
(y) ≤ 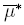 (y) holds for all y ∈ [0,1].
(y) holds for all y ∈ [0,1].
3.1. Normalized CTR+D method
By means of (14) - (17), the normalized version of (7) is (after some algebra 8):
where z = (t-a) / (b-a), α(z) = (α*(t)-a) / (b-a), and β*(z) = (β(t)-a) / (b-a). Therefore c*l = minz∈[0,1] α*(z), c*r = maxz∈[0,1]] β*(z) and c*M = (c*l + c*r) / 2 where
It should be noted that from (14) we have z, α *, β *, c*l, c*r, c*M ∈ [0; 1]. Similarly (9) - (10) are reduced to
where φ*(z) = φ(t) / (b - a)2 and ω*(z) = ω(t) / (b - a)2. Since φ(cl ) = 0 and ω(cr) = 0 then φ*(c*l ) = 0 and ω*(c*r) = 0. Therefore c*l and c*r are roots in [0, 1] of φ* and ω*. It is not difficult to verify that φ*; ω* 2 [-1/2, 1/2]. Although φ* and ω* are not in the unit interval, we only need their roots in [0, 1]. Additionally, there is a relation among φ* and ω*:
for all z ∈ [0, 1], where
By means of (14)-(17) the normalized version of (11) is (after some algebra):
where μ*NT
(y) = (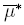 (y) +
(y) +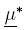 (y)) / 2 for all y ∈ [0, 1], and
(y)) / 2 for all y ∈ [0, 1], and
From (14) we have that c*NT ∈ [0, 1].
3.3. Normalized INT method
By means of (14)-(17), the normalized version of (12) is (after some algebra):
where
From (14) we have that c* INT ∈ [0, 1]. c* NT is given in Section 3.2, and δ* is given by
4. Results
4.1. Original Mendel and Liu's numerical examples
Mendel and Liu [11], [12] showed the following four numerical
1. Symmetric Gaussian MFs with uncertain deviation defined for all x ∈ X = [0, 10]:
2. Triangular LMF and Gaussian UMF defined for all x ∈ X = [-5; 14]:
3. Piecewise Gaussian MFs defined for all x ∈ X = [0, 10]:
)4. Piecewise Linear MFs defined for all x ∈ X = [1, 8]:
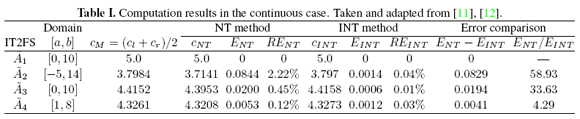
Their results are summarized in Table I. These authors used the following metrics for comparison:
1. Absolute error: 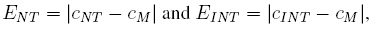
2. Percentage relative error:: 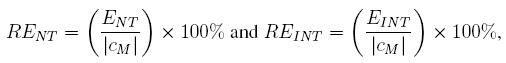
3. Difference of absolute errors: 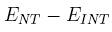 .
.
4. Absolute error ratio: 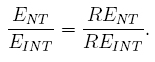
4.2. Normalized results
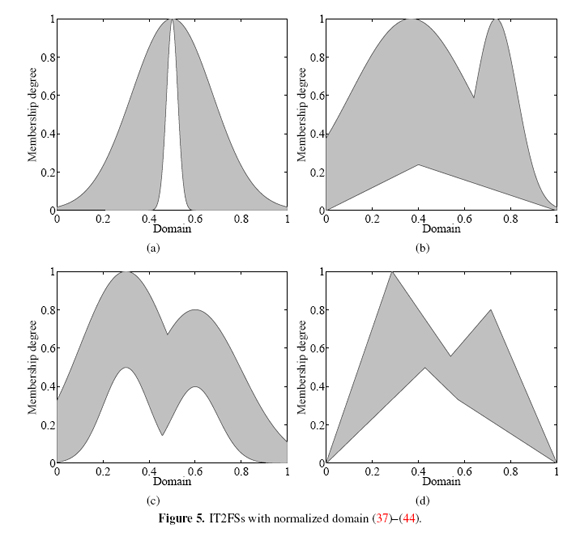
The corresponding IT2FSs with a normalized domain (37)-(44) are found by means of (29)-(36) by substituting x ∈ X by a + y(b - a), where ∈ 2 [0; 1]. The a and b values depend on the X-domain for each IT2FS. For example, for (35)-(36) we have a = 1 and b = 8.
1. Symmetric Gaussian MFs with uncertain deviation (Figure 5(a)) defined for all y ∈ [0, 1]:
2. Triangular LMF and Gaussian UMF (Figure 5(b)) defined for all y ∈ [0, 1]:
3. Piecewise Gaussian MFs (Figure 5(c)) defined for all y ∈ [0, 1]:
4. Piecewise Linear MFs (Figure 5(d)) defined for all y ∈ [0, 1]
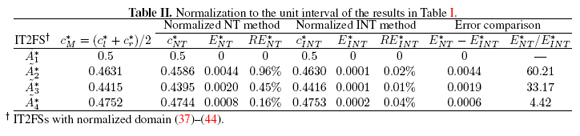
In Table II we show c*M = (cM - a) / (b - a), c* NT = (cNT - a) / (b - a) and c*INT = (cINT - a) / (b - a), which are the normalization to the unit interval of cM, cNT and cINT in Table I. We recalculated the following metrics:
1. Absolute error : 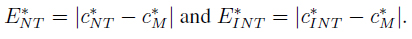
2. Percentage relative error: 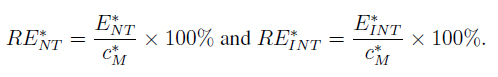
3. Difference of absolute errors: 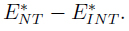
4. Absolute error ratio: 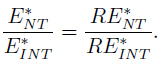
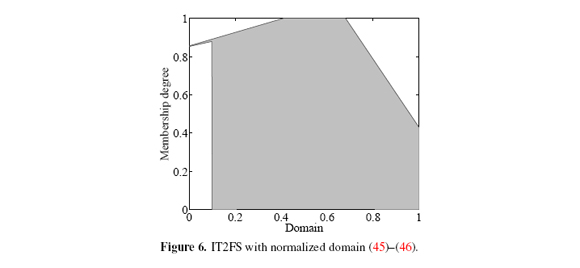
Let à be an IT2FS defined over [0, 1], and determined by piecewise linear MFs (Figure 6):
for all y ∈ [0, 1].
After calculating9 c* M, c* NT, c* INT, and the corresponding metrics for (45) - (46), we got the results in Table III.
5. Discussion
As we can see in Table III, our counterexample showed the following:
1. An absolute error E* NT = 0.1014. This is almost 23 times higher than E* NT = 0.0044 (worst case in Table II).
2. A percentage relative error RE*NT = 30.53%. This is almost 32 times higher than RE* NT = 0.96% (worst case in Table II).
3. An absolute error E* INT = 0.0725. This is almost 363 times higher than E* INT = 0.0002(worst case in Table II).
4. An percentage relative error RE* INT = 21.83%. This is almost 546 times higher than RE* INT = 0.04% (worst case in Table II).
In terms of error comparison E*NT - E* INT = 0:0289 and E* NT / E* INT = 1:3986, our example showed that*NTT is comparable (in magnitude) with respect to E* INT , in contrast with the results in Table II.
6. Conclusions
This paper showed a counterexample that exhibits higher errors than the corresponding errors in examples reported in the literature when comparing the NT and INT methods versus the CTR+D method. We chose an IT2FS with piecewise linear MFs as our counterexample, mainly due to its simplicity. All the domains (for examples and counterexample) were taken to the unit interval [0; 1] in order to reduce the effect of different domains on the metrics that we used for comparison. Additionally, all the variables involved in the three methods were normalized to the unit interval. We concluded, based on our results, that the NT and INT methods are not necessarily good approximations to the CTR+D method.
A. Source code for the counterexample in Section 4.3
The source code presented in this section was executed on MATLAB 7.14.0.739 (R2012a), on a laptop with Microsoft Windows XP Professional 32 bit, Intel(R) Atom(TM) CPU Z520 1.33 GHz,1014 MB of RAM. See the main text for a description of each variable in the following code.

References
[1] J. M. Mendel and R. I. John, "Type-2 fuzzy sets made simple," IEEE Transactions on Fuzzy Systems, vol. 10, no. 2, pp. 117-127, 2002.
[2] O. Castillo and P. Melin, Type-2 Fuzzy Logic: Theory and Applications, ser. Studies in Fuzziness and Soft Computing. Springer-Verlag Berlin Heidelberg, 2008, vol. 223.
[3] N. N. Karnik and J. M. Mendel, "Type-2 fuzzy logic systems : Type-reduction," in IEEE International Conference on Systems, Man, and Cybernetics, vol. 2, San Diego, California, USA, Oct. 1998, pp. 2046-2051.
[4] J. M. Mendel, R. I. John, and F. Liu, "Interval type-2 fuzzy logic systems made simple," IEEE Transactions onFuzzy Systems, vol. 4, no. 6, pp. 808-821, Dec. 2006.
[5] O. Salazar, J. Soriano, and H. Serrano, "Centroid of an interval type-2 fuzzy set: Continuous vs. discrete," Ingeniería, vol. 16, no. 2, pp. 67-78, 2011, ISSN 0121-750X.
[6] N. N. Karnik, J. M. Mendel, and Q. Liang, "Type-2 fuzzy logic systems," IEEE Transactions On Fuzzy Systems, vol. 7, no. 6, pp. 643-658, 1999.
[7] N. N. Karnik and J. M. Mendel, "Centroid of a type-2 fuzzy set," Information Sciences, vol. 132, pp. 195-220, 2001.
[8] S. Coupland and R. John, "An investigation into alternative methods for the defuzzification of an interval type-2 fuzzy set," in Proceedings of the 2006 IEEE International Conference on Fuzzy Systems, Vancouver, Canada, Jul. 2006, pp. 1425-1432.
[9] J. M. Mendel, "Type-2 fuzzy sets and systems: An overview," IEEE Computational Intelligence Magazine, vol. 2, no. 1, pp. 20-29, Feb. 2007.
[10] J. Aisbett, J. T. Rickard, and D. G. Morgenthaler, "Type-2 fuzzy sets as functions on spaces," IEEE Transactions on Fuzzy Systems, vol. 18, no. 4, pp. 841-844, Aug. 2010.
[11] J. M. Mendel and X. Liu, "New closed-form solutions for karnik-mendel algorithm defuzzification of an interval type-2 fuzzy set," in Proceedings of the 2012 IEEE International Conference on Fuzzy Systems (FUZZ-IEEE), Brisbane, QLD, Jun. 2012, pp. 1-8.
[12] --, "Simplified interval type-2 fuzzy logic systems," IEEE Transactions on Fuzzy Systems, vol. 21, no. 6, pp. 1056-1069, 2013.
[13] M. Nie and W. W. Tan, "Towards an efficient type-reduction method for interval type-2 fuzzy logic systems," in Proceedings of the IEEE International Conference on Fuzzy Systems (FUZZ 2008), 2008, pp. 1425-1432.
[14] S. Greenfield and F. Chiclana, "Accuracy and complexity evaluation of defuzzification strategies for the discretised interval type-2 fuzzy set," International Journal of Approximate Reasoning, vol. 54, pp. 1013-1033, 2013.
[15] J. M. Mendel, Uncertainty Rule-Based Fuzzy Logic Systems: Introduction and New Directions. Prentice-Hall PTR, 2001.
[16] D. Wu and M. Nie, "Comparison and practical implementation of type-reduction algorithms for type-2 fuzzy sets and systems," in Proceedings of the IEEE International Conference on Fuzzy Systems (FUZZ 2011), 2011, pp. 2131-2138.
[17] J. M. Mendel and H.Wu, "Uncertainty bounds and their use in the design of interval type-2 fuzzy logic systems," IEEE Transactions on Fuzzy Systems, vol. 10, no. 5, pp. 622-639, 2002.
[18] S. Greenfield, F. Chiclana, S. Coupland, and R. John, "The collapsing method of defuzzification for discretized interval type-2 fuzzy sets," Information Sciences, vol. 179, no. 13, pp. 2055-2069, 2009.
[19] J. M. Mendel and H. Wu, "Properties of the centroid of an interval type-2 fuzzy set, including the centroid of a fuzzy granule," in Proceedings of the 2005 International Conference on Fuzzy Systems (FUZZ-IEEE 2005), 2005, pp. 341-346.
[20] --, "New results about the centroid of an interval type-2 fuzzy set, including the centroid of a fuzzy granule," Information Sciences, vol. 177, pp. 360-377, 2007.
[21] O. Salazar and J. Soriano, "Generating embedded type-1 fuzzy sets by means of convex combination," in Proceedings of the 2013 IFSA World Congress NAFIPS Annual Meeting, Edmonton, Canada, Jun. 2013, pp. 51-56.
[22] --, "Convex combination and its application to fuzzy sets and interval-valued fuzzy sets I," Applied Mathematical Sciences, vol. 9, no. 22, pp. 1061-1068, 2015, ISSN 1312-885X.
[23] --, "Convex combination and its application to fuzzy sets and interval-valued fuzzy sets II," Applied Mathematical Sciences, vol. 9, no. 22, pp. 1069-1076, 2015, ISSN 1312-885X.
[24] J. M. Mendel and F. Liu, "Super-exponential convergence of the Karnik-Mendel algorithms for computing the centroid of an interval type-2 fuzzy set," IEEE Transactions on Fuzzy Systems, vol. 15, no. 2, pp. 309-320, Apr. 2007.
[25] X. Liu and J. M. Mendel, "Connect karnik-mendel algorithms to root-finding for computing the centroid of an interval type-2 fuzzy set," IEEE Transactions on Fuzzy Systems, vol. 19, no. 4, pp. 652-665, 2011.
1 Centroid type-reduction is classified into two forms: discrete and continuous [5]. From a discretization of the MFs it is possible to switch from continuous to discrete. This paper discusses the continuous version, but several results are applied to the discrete case.
2An alternative notation as interval set is CÃ = 1 / [c l , c r ]. In this paper we use standard mathematical notation [10].
3It is called the "KM + Defuzzification" method in [11], [12].
4The image of μAe is Im(μAe ) = {μA e (x) ‌ x ∈ X}.
5A comparative study (by means of statistical analysis) was carried out in [14] in order to compare accuracy and complexity for the Exhaustive Defuzzification method [15] versus the Karnik-Mendel iterative procedure [7] (EIASC algorithm [16, section III]), the Wu-Mendel approximation (WM algorithm [17, appendix III, pp. 635]), the Greenfield-Chiclana Collapsing Defuzzifier (collapsing algorithm [18]), and the NT method [13].
6 In this paper all the MFs are supposed to be Riemann-Integrable.
7 In several papers on the centroid, X is taken as (- ∞ , ∞ ) with the assumption that all integrals are convergent. However, over this domain the centroid of an IT2FS could not exist. See [5, sec. 2.1] for an example.
8The substitution x = a + y(b - a) yields dx = (b - a)dy, which is the required substitution for dx. The other variables are obtained by performing the corresponding substitutions.
9 In Appendix A we present a source code for the numerical calculation.
Licencia
A partir de la edición del V23N3 del año 2018 hacia adelante, se cambia la Licencia Creative Commons “Atribución—No Comercial – Sin Obra Derivada” a la siguiente:
Atribución - No Comercial – Compartir igual: esta licencia permite a otros distribuir, remezclar, retocar, y crear a partir de tu obra de modo no comercial, siempre y cuando te den crédito y licencien sus nuevas creaciones bajo las mismas condiciones.


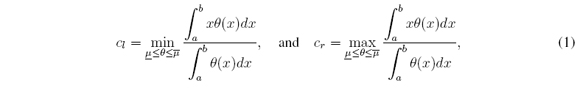
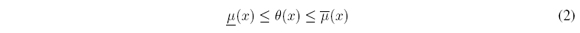
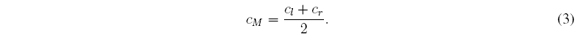
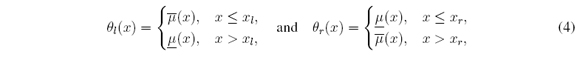
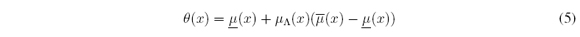
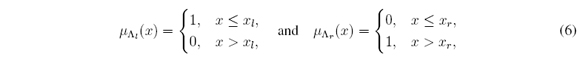
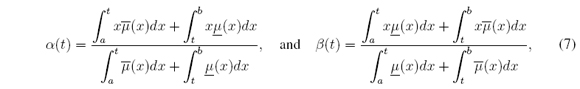
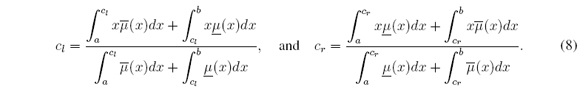
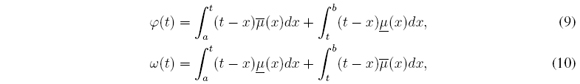
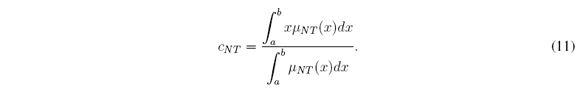
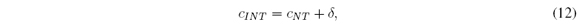
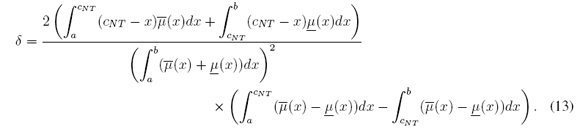
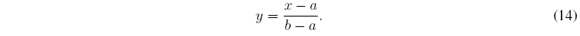
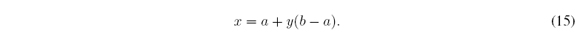
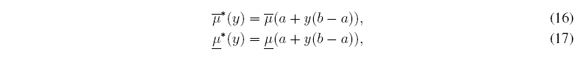
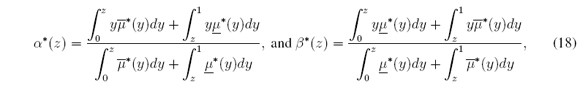
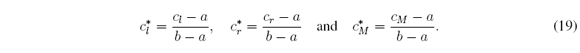
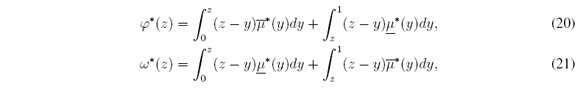
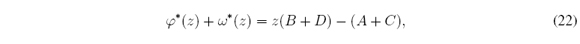
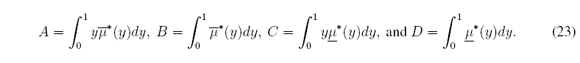
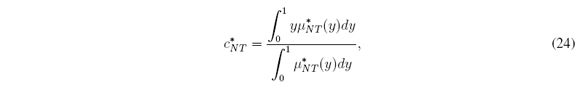
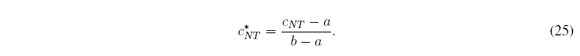
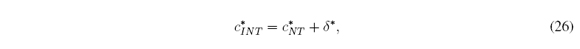
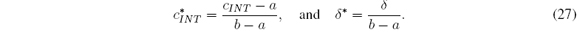
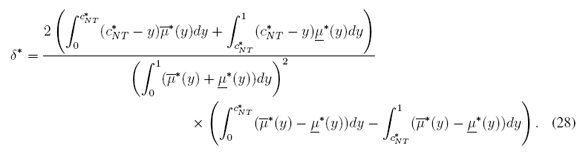
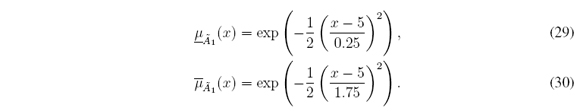
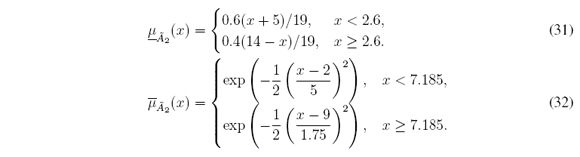
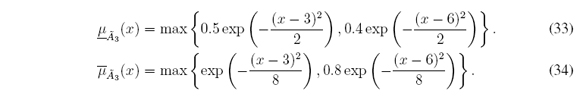

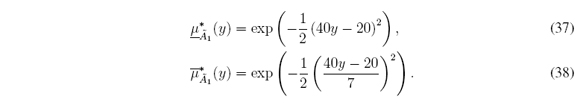
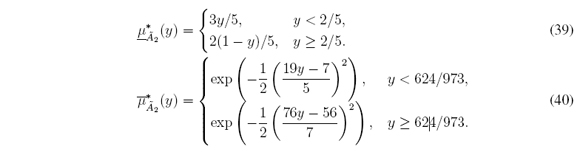
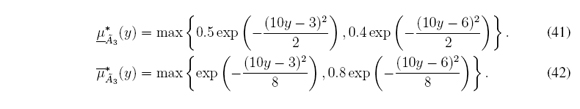






2.jpg)