DOI:
https://doi.org/10.14483/23448393.2827Publicado:
2001-11-30Número:
Vol. 7 Núm. 2 (2002): Julio - DiciembreSección:
Ciencia, investigación, academia y desarrolloSíntesis de diagramas de radiación con agrupaciones circulares de antenas aplicables en sistemas umts 3g
Pattern synthesis with circular arrays for 3g umts systems
Palabras clave:
Síntesis de diagramas de radiación, Agrupaciones Cilíndricas, Agrupaciones Circulares. (es).Descargas
Referencias
. C. Suárez, M. Ferrando. "Síntesis de Diagramas de Radiación con Agrupaciones Cilíndricas Aplicables en Sistemas 3G UMTS". Revista facultad de Ingeniería U. Antioquia, junio 2003, No 28
. Pagana Enrico. "Evolution of Base Station Antennas for Radio mobile Communications" enrico.pagana@tinn.itt
. L. C. Godara, "Application of Antenna Arrays to Mobile Communications", part 1 and part 2. Proceedings of IEEE, Vol.85, pp.1031-1245.
. Pattan. Robust Modulation Methods and Smart Antennas in Wireless Commmunications. Prentice Hall PTR 2000.
. Butler, Lowe. "Beam forming Matrix Semplifies Design of Electronically Scanned Antennas". Electronic Design. 1961.
. A. W. Rudge, et al, The Handbook of Antenna Design, IEE pres. 1986.
. Rahim, T. Directional pattern synthesis in circular arrays of directional antennas, Ph. D. Thesis, Univ. Of London, 1980.
. Lars. Josefsson, H. Steyskal. Methods and Software Tools for the Design of Antenas and Arrays, Advanced Short Course, Universidad de Santiago de Compostela, España, sept. 4, 2002.
. W. Berndt, "Ermittlung der Richtcharakteristik durch Fourier-Entwicklug", Hochfrequenz und Elektroakustik, 1934.
. S. A. Schelkunoff, "A mathematical theory of linear arrays", Bell System Tech, No.22, 1943, p. 80-107.
. C. L. Dolph, "A current distribution for broadside arrays which optimizes the relationship between beam width and side-lobe level", Proc. IRE, No. 34, 1946, p. 335-348.
. P. M. Woodward, J. D. Lawson, "The theoretical precision with which an arbitrarily radiation pattern may be obtained from a source of finite size", IEE, Proc. No. 95, Pt. III, 1948, p. 363-370.
. J. Eaton, L. Eyges, G. MacFarlane, " Power Pattern synthesis", MIT Rad. Lab. Series, vol. 12, 1949.
. E. N. Gilbert, S. P. Morgan "Optimization design of directive antenna subject toRandom variation", BJTJ, 34, 1955, p. 637-663.
. E. bayliss, "Monopulse antenna difference pattern with characteristics similar to Taylor pattern", Bell System Tech, 1968.
. H. Steyskal, "weighted LMS Power Pattern synthesis", IEEE, Trans. AP, 1970.
. V. Popovkin, Yu Sedel'nikov, "pattern synthesis Using Linear programming", Radio Engineering and Electronic Physics, 1972.
. H. Orchard, R. S. Elliot, G. J. Stern, "The Orchard-Elliot-Stern Method", IEE, Proc. Pt. H, No. 1, 1984.
. O. Bucci, G. Franceschetti, G. Mazzarella, "Method of Alternating Projections", IEE, Proc. Pt. H. 1990.
. R. Vescovo, "Constrained and Unsconstrained Synthesis of Array Factor For Circular Arrays". IEEE Trans. Antennas Propagat. vol 43. No12, pp .1405-1410, December 1995.
. F. I. Tseng, D. K. Cheng. "Pattern Synthesis of Circular Arrays with Many Directive Elements". IEEE Trans .Antennas Propagat; vol. AP-2, No1, pp .758. Nov. 1968.
. I. D. Longstaff, P.E. K. Chow, D. E. N. Davis, "Directional Properties of Circular Arrays", IEE, Proc. No. 114, June, 1967, p. 717-718.
. S. Prasad, R.Charan, "On the Constrained Synthesis of Array Patterns with. Applications to Circular and Arc Arrays", IEEE Trans .Antennas Propagat;vol. AP- 32, No 7 , pp 725-730, july 1984.
. Goto, Y. Tsunoda,"Side Lobe Reduction of Arrays with a Constant Excitation Amplitude" IEEE Trans .Antennas Propagat;vol AP25, No6, pp .896-897,December 1977.Harrington,
. Roger F Harrington. Time Harmonic Electromagnetic Fields. New York. McGraw- Hill. 1961. p. 225.
. C. Suárez, M. Ferrando, A. valero "Radiación de Dipolos Frente a Cilindro Metálico Infinito". Simposio URSI, La Coruña España, septiembre 2003.
. John C. Herper, et al. "Element pattern of an Axial Dipole in a Cylindrical Phased Array". IEEE Trans AP-33, No. 3, March 1985, p. 259-272.
. L. B. Felsen, N. Marcuvits. Radiation and Scattering of waves. IEEE pres. 1984.
. A. C. Cardama et al, Antenas, España, Ediciones UPC, 2ª Ed. Nov. 2002.
Cómo citar
APA
ACM
ACS
ABNT
Chicago
Harvard
IEEE
MLA
Turabian
Vancouver
Descargar cita
Ingeniería, 2002-00- vol: nro:2 pág:104-108
Síntesis de diagramas de radiación con agrupaciones circulares de antenas aplicables en sistemas umts 3g
Pattern synthesis with circular arrays for 3g umts systems
Carlos Arturo Suárez F.
Miembro grupo de investigación en Comuinicaciones, Universidad Distrital Francisco José de Caldas.
Miguel Ferrando Bataller
Profesor Universidad Politécnica de Valencia.
Alejandro Valero Nogueira
Profesor Universidad Politécnica de Valencia.
José Noé Poveda Z.
Miembro grupo de investigación en Comuinicaciones, Universidad Distrital Francisco José de Caldas.
Resumen
Este artículo describe la síntesis de diagramas de radiación con agrupaciones circulares de antenas utilizando elementos directivos, aplicables en los sistemas de antenas inteligentes (Smart Antennas) para la estación base, como una solución viable en sistemas UMTS y frente a las nuevas exigencias del mercado.
Como elemento básico de diagrama de radiación directivo, se utilizarán hilos infinitos con corriente constante, frente a un cilindro metálico infinito, cuyos resultados serán fácilmente extensibles al caso de dipolos finitos frente a un cilindro (figura 3).
La técnica utilizada será la de Fourier, como continuación de artículo Suárez -Ferrando [1] y se plantea un método para sintetizar diagramas de radiación utilizando una agrupación de N antenas tipo hilo infinito con corriente constante uniformemente distribuidas sobre un circulo y frente a un cilindro metálico infinito. Las corrientes que permiten la síntesis del diagrama deseado se podrán determinar con una expresión que se deducirá en el artículo.
Palabras Clave:
Síntesis de diagramas de radiación; Agrupaciones Cilíndricas; Agrupaciones Circulares.
Abstract
This article describes the synthesis of radiation patterns with circular antenna arrays using directive elements, applicable in the intelligent antennas systems (Smart Antennas) for the base station, like a viable solution in UMTS systems and in front of the new demands of the market.
As a basic element of directive radiation pattern, the infinite filament of constant current will be used, in front of a metallic infinite cylinder whose results will be easily expandable to the case of finite dipoles in front of infinite metallic cylinder.
The used technique will be that of Fourier, as article continuation Suárez - Ferrando [1] and a method for synthesizing the radiation pattern with antenna array of N infinite filament of constant current uniformly disposed around a circular ring an in front of a cylinder is proposed.
The required excitation currents are determined from a deduced formula in the paper.
Key Words:
Pattern Synthesis; Cylindrical Arrays, Circular Arrays.
I. INTRODUCCIÓN
Los sistemas de comunicaciones móviles han experimentado un incremento en tráfico y en la variedad y calidad de los servicios ofrecidos por todo el mundo. Actualmente los operadores de celular están trabajando en el proceso de transición de sistemas análogos para comunicación de voz a los sistemas digitales que permiten comunicación de voz y datos; planteando la necesidad de incrementar la capacidad del sistema, lo cual conduce a los sistemas de antenas inteligentes (Smart Antennas).
Los nuevos servicios de alta velocidad de datos como Internet, música y transmisiones de video requieren de la ampliación de capacidad en las redes. Por esta razón los fabricantes y operadores están desarrollando los sistemas 2.5G y 3G como: GPRS (General Packed Radio Service) y UMTS (Universal Mobile Telecommunications Systems) para Europa y Japón y el CDMA2000 para lejano oriente y USA [2].
Para dar un orden de magnitud al fenómeno actual, la evolución de la familia de sistemas móviles de tercera generación 3G, supone un crecimiento en capacidad de 13Kbs en los sistemas 2G, GSM (Voz) y 171.2 Kbs en los sistemas 2.5G, GPRS y tienden a velocidades arriba de 2048 Kbs en los sistemas 3G UMTS para usuarios de baja movilidad en áreas de cubrimiento local. Una de las alternativas de solución al problema planteado es adoptar sistemas de antenas inteligentes y en particular con agrupaciones cilíndricas o circulares de antenas para la estación base, aparte de los mejoramientos que se deben hacer en la antena del móvil.
Antenas Inteligentes (Smart Antennas)
La teoría básica no es nueva y ha sido aplicada en sistemas de radar militar, material de guerra. En comunicaciones móviles las antenas inteligentes son agrupaciones planas de elementos radiantes y/o sub.-agrupaciones capaces de cambiar su diagrama de radiación dinámicamente para reducir ruido, interferencias cocanal y multitrayectoria.
En la mayoría de sistemas de antenas inteligentes se conoce como determinar la ubicación exacta del usuario. Ellos son capaces de seguirlo y enfocarlo para recibir energía solamente en la dirección deseada de arribo, creando al mismo tiempo nulos en las direcciones de usuarios indeseados que causan interferencia.
El uso de diagramas de radiación tipo pincel dirigibles, a cambio de omnidireccionales o sectoriales generan muchas ventajas pero el precio que hay que pagar es incrementar la complejidad de los equipos de las estaciones base como se discute en, [3], [4].
II AGRUPACIONES CILÍNDRICAS DE ANTENAS
Diversos servicios como: radio determinación, navegación aérea, espacial y marítima, estaciones base para telefonía móvil entre otras, han encontrado interesantes prestaciones en las Configuraciones de agrupaciones donde los elementos son colocados sobre un círculo o un cilindro circular. En los estudios han utilizado antenas isotrópicas, dipolos, monopolos, parches, ranuras etc.
Los diagramas obtenidos con este tipo de agrupaciones ofrecen ventajas como: un amplio cubrimiento angular (360º) con un pequeño cambio en el ancho de banda o nivel de lóbulos laterales, una gran flexibilidad en su forma permitiendo haces tipo pincel direccionables, múltiple pincel, variadas formas como: sectoriales, omnidireccionales y otras formas, aplicables en formación adaptativa de haces para búsqueda de señales deseadas y control de ruido no deseado.
El poco desarrollo que se tuvo en el pasado pudo ser ocasionado por la dificultad de excitar la agrupación circular con los valores apropiados de fase y amplitud que son en general más complejos que en las agrupaciones lineales, hoy en día este problema es superado con la optimización en el diseño de matrices de Butler [5].
Otras características adicionales son: los efectos de los Lóbulos de difracción "grating lobe" no son tan pronunciados como en agrupaciones planas, ciertos elementos pueden no ser visibles en ciertas direcciones lo cual permite desconectarlos afectando la radiación en los lóbulos secundarios sin consecuencias graves para el diagrama final.
La simetría básica de una agrupación circular ofrece otras ventajas adicionales a las ya expuestas como es la de permitir compensar los efectos del acoplamiento mutuo entre los elementos de la agrupación mediante la escogencia apropiada de la excitación de la agrupación en una serie de componentes espaciales simétricos.
El uso de elementos con diagramas de radiación directivos permite una mejora adicional como es la de presentar una estabilidad en la amplitud de los modos ante la variación en frecuencia como se muestra en [6], [7].
Síntesis de Diagramas de Radiación con Agrupaciones de Antenas.
La capacidad de las agrupaciones para modificar el diagrama de radiación de la antena básica puede aprovecharse para sintetizar un diagrama de radiación que cumpla con determinadas especificaciones mediante la selección apropiada de la amplitud y fase de las corrientes.
Los métodos de síntesis de diagramas de radiación han mostrado una constante evolución y se puede notar que hasta el año 1970 aproximadamente, las técnicas más utilizadas eran analíticas y a partir de este año las técnicas preferidas son las numéricas. En una revisión de las publicaciones hasta hoy, se puede concluir que sigue en constante estudio el problema de síntesis, con un incremento notorio en los últimos años de los artículos sobre este aspecto.
Para el caso de síntesis con agrupaciones lineales se encuentran diversas técnicas enumeradas cronológicamente, [8] con los primeros investigadores que las utilizaron (algunas de estas aplicadas a agrupaciones circulares) como: Fourier (1934) , [9]; Schelkunoff (1943), [10]; Dolph-Chebyshev (1946), [11]; Método de Woodward and lawson (1948), [12]; Síntesis de diagrama de potencia (1949), [13]; T. T. Taylor (1955), [14]; Diagrama diferencia con antena monopulso, (1968), [15]; Síntesis de diagramas de potencia con pesado LMS, (1970), [16]; Síntesis de diagramas utilizando programación lineal (1972), [17]; Método de Orchard-Elliot-Stern, (1984), [18]; Método de las proyecciones alternadas, (1990), [19].
Las técnicas de Síntesis más usuales con agrupaciones circulares, mencionando algunos de los investigadores que las utilizan son: Fourier, [20], [21], [22] aplicado a la excitación de la agrupación y del diagrama de radiación en campo lejano, este método es muy atractivo para síntesis de diagramas directivos; Síntesis con restricciones, [20], [23]; Síntesis de diagramas utilizando programación lineal, [24]; Síntesis con elementos directivos, [6], [7].
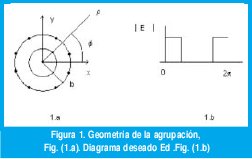
En este artículo se analizará el problema de una agrupación con N fuentes de hilo infinito de corriente constante sobre un anillo de radio (b), frente a un cilindro de radio (a), figura (1.a) calculando inicialmente el campo de radiación Ez, para posteriormente utilizarlo en aplicaciones de síntesis de diagramas de radiación deseados Ed ; en particular se sintetizarán diagramas de radiación con características sectoriales figura (1.b).
III. SÍNTESIS CON AGRUPACIONES CIRCULARES DE ANTENAS DIRECTIVAS
La expresión para la función de Green en espacio libre para campos en dos dimensiones de un hilo de corriente constante y longitud infinita, fue deducida en [25] como:
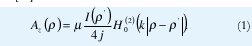
El campo eléctrico se expresa como:

El campo total ETz generado por una agrupación de N hilos de longitud infinita y corriente constante sobre un círculo de radio a esta dado por:

Aplicando teorema de adición para funciones de Hankel y para el caso a < < b , la ecuación (2) queda:
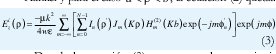
Donde la ecuación (3) representa el campo incidente sobre el cilindro y Φ 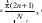 determina la ubicación de las fuentes sobre el círculo con corriente I n (' ) = In exp(jαn) , para n = 0,1,2,3N-1.
determina la ubicación de las fuentes sobre el círculo con corriente I n (' ) = In exp(jαn) , para n = 0,1,2,3N-1.
La expresión para el campo disperso Ezs, está dado por:
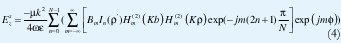
La condición de contorno sobre la superficie del cilindro exige que:
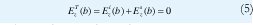
Aplicando la condición de contorno (5) a las ecuaciones (3) y (4), se determina el término Bm , y el campo total Ez esta dado por:
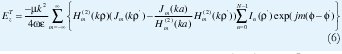
La expresión para el campo de radiación ETz , tomando la aproximación asintótica para las funciones de Hankel en el caso Kρ ⇒ ∞ y tal que ρ= b ; nos lleva a:

La expresión final para el campo lejano (ETzN) normalizado, generado por N fuentes de hilo infinito de corrientes constantes sobre un círculo de radio (b) frente a un cilindro de radio (a) está dada por:
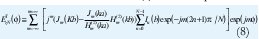
La expresión (8) se puede interpretar como la expansión en serie de Fourier del campo ETzN:
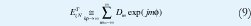
Donde los coeficientes de Fourier Dm están dados por:
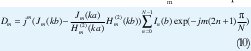
Dado que el patrón deseado Ed es periódico, se puede expandir en serie de Fourier como se nota a continuación:
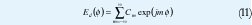
Donde los coeficientes Cm son determinados por:
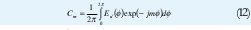
La series infinitas (9) y (11) se truncarán a 2M + 1 términos por razones prácticas en cuanto al número máximo de elementos que se pueden utilizar y el espaciamiento mínimo entre elementos y por otra parte para obtener una única solución.
Igualando las series del patrón deseado y la agrupación y truncándolas a 2M+1 términos se tiene:
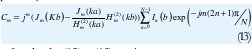
Igualando (12) y (13) se tiene:
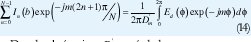
Donde el término Dm está dado por:
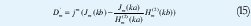
Multiplicando a ambos lados de la ecuación (14) por el término: exp jm (2nΦ+1)/N
Y sumando las ecuaciones en (m) al lado derecho se tiene:
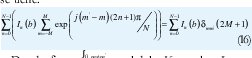
Donde δmm= 1,,m m es el delta Kronecker; La expresión final para las corrientes es dada por:
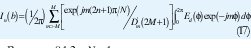
Para: n = 0,1,2....N - 1
IV. DIAGRAMAS DIRECTIVOS ESTUDIADOS
4.1. Hilo infinito con corriente constante frente a un cilindro infinito de radio (a)
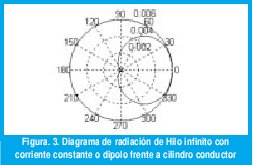
La expresión para el campo total generado por un hilo infinito con corriente constante frente a un cilindro infinito de radio (a) figura 2, fue deducida en [25] y su ecuación (18) y campo de radiación ( ρ>ρ), se muestran a continuación en figura 3 y se comparan contra las ecuaciones deducidas (19) para el caso de un dipolo finito frente a cilindro infinito figura 3:

El campo de radiación para un hilo infinito con corriente constante frente a un cilindro infinito conductor está dado por:
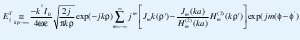
Normalizando la ecuación (18) para una distancia constante del punto de observación se tienen los resultados notados en figura 3.
4.2. Hilo finito (dipolo) frente a un cilindro conductor infinito.
Para el caso de un hilo finito (dipolo) frente a un cilindro conductor infinito figura 3; las ecuaciones asociadas y resultados obtenidos en [26] se muestran a continuación:
La solución de la ecuación de onda para el caso de un dipolo desplazado del origen es:
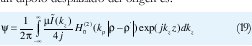
La solución de la ecuación de onda para el caso de campo radiado (ρ > ρ) de un dipolo finito frente a un cilindro conductor infinito está dada por:
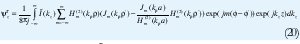
de corriente Ik2 en el dipolo y está dada por:
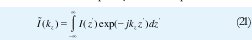
Utilizando la aproximación asintótica (ρ >>ρ) para la función de Hankel en ?, aplicando el método de "Saddle Point" [27], [28] para solucionar la integral impropia en (20) y luego de calcular la transformada de la distribución de corriente en un dipolo [29] y aplicar la identidad 1.a, se llega a que el campo de radiación para un dipolo finito frente a un cilindro infinito, y para θ= π/2 está dado por:
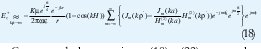
Comparando las ecuaciones (18) y (22), se nota la similitud de los resultados, para el caso de θ=π/2 en (22), notando que la diferencia básica está en las constantes y en los términos relacionados con la distancia. Los diagramas de radiación directivos para los dos casos se presentan en la figura 3.
V. Resultados Numéricos
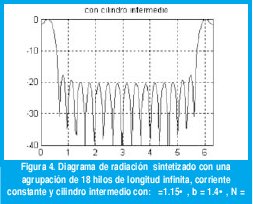
Utilizando la ecuación (17) antes deducida se calculan, las corrientes que permiten sintetizar un diagrama ideal tipo sectorial figura (1.b) y en la figura 4, se muestra el diagrama sintetizado con una agrupación de N = 18 hilos infinitos con corriente constante sobre un anillo circular de radio b = 1.4· , frente a un cilindro metálico infinito de radio α= 1.15λ.
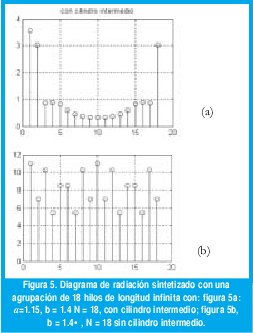
Las magnitudes de las corrientes necesarias para la síntesis se muestran en figura 5.a y se comparan con los valores requeridos para el caso de agrupación con b = 1.4· , N = 18 sin cilindro intermedio, utilizando las ecuaciones deducidas en [1], los resultados se muestran en la figura 5b.
VI. CONCLUSIÓN
Como se aprecia en figura 4 el diagrama obtenido presenta una buena aproximación al diagrama sectorial deseado Ed con un mínimo error cuadrático medio, y con un nivel de lóbulo principal a secundario (NLPS) mayor de 18(DB), caracterizando una agrupación circular con elementos directivos. Los valores de las corrientes necesarias para la síntesis con cilindro intermedio, presentan un comportamiento más uniforme (deseable desde el punto de vista práctico) que los obtenidos para la misma agrupación pero sin cilindro intermedio, que sería el caso de una agrupación circular con elementos omnidireccionales.
El cálculo de las corrientes se hace mediante las ecuaciones deducidas, permitiendo diseño de agrupaciones con muchos elementos y cuyos valores dependen directamente del diagrama deseado en cuanto a forma y dirección de máximo.
VI. REFERENCIAS
[1]. C. Suárez, M. Ferrando. "Síntesis de Diagramas de Radiación con Agrupaciones Cilíndricas Aplicables en Sistemas 3G UMTS". Revista facultad de Ingeniería U. Antioquia, junio 2003, No 28
[2]. Pagana Enrico. "Evolution of Base Station Antennas for Radio mobile Communications" enrico.pagana@tinn.itt
[3]. L. C. Godara, "Application of Antenna Arrays to Mobile Communications", part 1 and part 2. Proceedings of IEEE, Vol.85, pp.1031-1245.
[4]. Pattan. Robust Modulation Methods and Smart Antennas in Wireless Commmunications. Prentice Hall PTR 2000.
[5]. Butler, Lowe. "Beam forming Matrix Semplifies Design of Electronically Scanned Antennas". Electronic Design. 1961.
[6]. A. W. Rudge, et al, The Handbook of Antenna Design, IEE pres. 1986.
[7]. Rahim, T. Directional pattern synthesis in circular arrays of directional antennas, Ph. D. Thesis, Univ. Of London, 1980.
[8]. Lars. Josefsson, H. Steyskal. Methods and Software Tools for the Design of Antenas and Arrays, Advanced Short Course, Universidad de Santiago de Compostela, España, sept. 4, 2002.
[9]. W. Berndt, "Ermittlung der Richtcharakteristik durch Fourier-Ent- wicklug", Hochfrequenz und Elektroakustik, 1934.
[10]. S. A. Schelkunoff, "A mathematical theory of linear arrays", Bell System Tech, No.22, 1943, p. 80-107.
[11]. C. L. Dolph, "A current distribution for broadside arrays which optimizes the relationship between beam width and side-lobe level", Proc. IRE, No. 34, 1946, p. 335-348.
[12]. P. M. Woodward, J. D. Lawson, "The theoretical precision with which an arbitrarily radiation pattern may be obtained from a source of finite size", IEE, Proc. No. 95, Pt. III, 1948, p. 363-370.
[13]. J. Eaton, L. Eyges, G. MacFarlane, " Power Pattern synthesis", MIT Rad. Lab. Series, vol. 12, 1949.
[14]. E. N. Gilbert, S. P. Morgan "Optimization design of directive antenna subject toRandom variation", BJTJ, 34, 1955, p. 637-663.
[15]. E. bayliss, "Monopulse antenna difference pattern with characteristics similar to Taylor pattern", Bell System Tech, 1968.
[16]. H. Steyskal, "weighted LMS Power Pattern synthesis", IEEE, Trans. AP, 1970.
[17]. V. Popovkin, Yu Sedel'nikov, "pattern synthesis Using Linear programming", Radio Engineering and Electronic Physics, 1972.
[18]. H. Orchard, R. S. Elliot, G. J. Stern, "The Orchard-Elliot-Stern Method", IEE, Proc. Pt. H, No. 1, 1984.
[19]. O. Bucci, G. Franceschetti, G. Mazzarella, "Method of Alternating Projections", IEE, Proc. Pt. H. 1990.
[20]. R. Vescovo, "Constrained and Unsconstrained Synthesis of Array Factor For Circular Arrays". IEEE Trans. Antennas Propagat. vol 43. No12, pp .1405-1410, December 1995.
[21]. F. I. Tseng, D. K. Cheng. "Pattern Synthesis of Circular Arrays with Many Directive Elements". IEEE Trans .Antennas Propagat; vol. AP-2, No1, pp .758. Nov. 1968.
[22]. I. D. Longstaff, P.E. K. Chow, D. E. N. Davis, "Directional Properties of Circular Arrays", IEE, Proc. No. 114, June, 1967, p. 717-718.
[23]. S. Prasad, R.Charan, "On the Constrained Synthesis of Array Patterns with. Applications to Circular and Arc Arrays", IEEE Trans .Antennas Propagat;vol. AP- 32, No 7 , pp 725-730, july 1984.
[24]. Goto, Y. Tsunoda,"Side Lobe Reduction of Arrays with a Constant Excitation Amplitude" IEEE Trans .Antennas Propagat;vol AP-25, No6, pp .896-897,December 1977.Harrington,
[25]. Roger F Harrington. Time Harmonic Electromagnetic Fields. New York. McGraw- Hill. 1961. p. 225.
[26]. C. Suárez, M. Ferrando, A. valero "Radiación de Dipolos Frente a Cilindro Metálico Infinito". Simposio URSI, La Coruña España, septiembre 2003.
[27]. John C. Herper, et al. "Element pattern of an Axial Dipole in a Cylindrical Phased Array". IEEE Trans AP-33, No. 3, March 1985, p. 259-272.
[28]. L. B. Felsen, N. Marcuvits. Radiation and Scattering of waves. IEEE pres. 1984.
[29]. A. C. Cardama et al, Antenas, España, Ediciones UPC, 2ª Ed. Nov. 2002.
Carlos Arturo Suárez F.
Profesor asistente Universidad Distrital "Francisco José de Caldas" y Estudiante de Doctorado, Universidad Politécnica de Valencia. csuarez33@udistrital.edu.co
Miguel Ferrando Bataller Alejandro Valero Nogueira
Profesores Titulares, Universidad Politécnica de Valencia. mferrand@dcom.upv.es.
José Noé Poveda
Profesor asistente, Universidad Distrital "Francisco José de Caldas".
Creation date:
Licencia
A partir de la edición del V23N3 del año 2018 hacia adelante, se cambia la Licencia Creative Commons “Atribución—No Comercial – Sin Obra Derivada” a la siguiente:
Atribución - No Comercial – Compartir igual: esta licencia permite a otros distribuir, remezclar, retocar, y crear a partir de tu obra de modo no comercial, siempre y cuando te den crédito y licencien sus nuevas creaciones bajo las mismas condiciones.




2.jpg)