Modelamiento de estaciones TransMilenio mediante Autómatas Celulares: lecciones aprendidas

Modeling TransMilenio’s stations using Cellular Automata: lessons learned

Camilo Alfonso Rodríguez Garzón, Universidad Distrital Francisco José de Caldas, camilo.18.20@gmail.com

Recibido: 10-08-2014. Modificado: 01-12-2014. Aceptado: 02-12-2014.

Resumen

Partiendo de un modelo que permite simular el congestionamiento en una estación de TransMilenio, se presenta una reflexión acerca de las consecuencias del uso del paradigma utilizado (autómatas celulares), así como de aspectos idiosincráticos que repercuten en el modelo. Se discuten simultáneamente los desafíos técnicos e intelectuales que ello implica: simular las complejidades de un sistema en apariencia simple, pero que exhibe una enorme diversidad de comportamientos y variables plantea afrontar nuevos enfoques y técnicas. El Ingeniero, bajo su status quo en la sociedad, debe replantear sus esquemas y combinar disciplinas tradicionales y emergentes para enfrentar dichos retos. La experiencia que se recopila, da cuenta de ello.

Palabras claves: Autómata Celular, cultura TransMilenio.

Abstract

A discussion is carried out on the basis of a model that simulates TransMilenio’s stations overcrowding, about the consequences of the paradigm of choice (Cellular Automata) and the cultural aspects of the users. This is done taking into account the implications involved: the fact of analyzing complexities in real life open-up new perspectives, revealing that established schemes must be questioned in order to react and handle them. Any engineer committed to the society that educated him must be aware that modern challenges imply new skills, particularly, the ability to combine the old and the new, regarding systems enginnering paradigms.

Keywords: Cellular Automata, TM idiosyncracy, Engineering

1. Introducción

Es curioso observar cómo la complejidad de diferentes objetos y situaciones, como un ecosistema, la bolsa de valores o un tornado se encuentra regida por simples interacciones locales entre sus componentes. Esta característica, descrita por diferentes autores como pilar de los sistemas complejos [1, 2] es aprovechada en un reciente estudio [3], para simular la situación que se presenta dentro de una estación del sistema de buses rápidos de Bogotá TransMilenio. Dicho estudio toma como base un modelo de Autómata Celular (AC), concebido para evolucionar mediante reglas simples, para así obtener la esencia del comportamiento de una multitud a lo largo de un día normal de operación del sistema. De ese trabajo se parte aquí para analizar las características, ventajas y limitaciones del uso de un AC. El artículo se divide en cuatro secciones: la primera de ellas como una recapitulación de hechos, la segunda cuenta lo relativo al uso de los AC, la tercera toca los aspectos idiosincráticos de la sociedad que consume TransMilenio y finalmente una conjugación de las partes a manera de conclusión.

2. Recapitulación de hechos

Con el objetivo de permitir la comprensión de lo que se habla, se pone en contexto al lector: TransMilenio es el sistema de buses de tránsito rápido construido en la ciudad de Bogotá, Colombia, ideado como eje principal para la modernización y ampliación del sistema de transporte público bogotano cuyos componentes son principalmente estaciones, buses y carriles exclusivos que bajo un sistema de gestión permite la organización de los mismos en diferentes horas por medio de rutas con el objetivo de transportar personas. La principales ventajas de este sistema son la exclusividad de carriles vehiculares por donde se mueven los buses de manera preferente y su detención en puntos estratégicos. El asunto de interés es el congestionamiento que se ha venido presentando en las estaciones de abordaje, sin faltas, en las horas de mayor flujo de personas (horas pico) que es cuando estas van de sus hogares a lugares de trabajo por la mañana y viceversa en la tarde.

Esta situación, observada como una interacción entre pasajeros que toman buses genera comportamientos en la escala de multitud como congestiones, formación de líneas y oscilaciones que son el resultado básicamente de personas en movimiento que se dirigen hacia el frente (bidireccional) y de personas esperando la llegada del bus. De aquí a que sea factible la construcción de modelos que hagan uso de la computación celular para tomar todas las ventajas que esto implica [1, 2, 4]: determinar reglas locales de interacción entre los componentes que mediante la evolución del sistema muestren rasgos a escalas superiores que reproduzcan aquellos de la realidad.

De los modelos computacionales más simples para lograrlo se encuentran los AC, los cuales son un sistema cuyo espacio es un arreglo de celdas donde agentes y reglas evolucionan en el tiempo desde una configuración inicial [5]. Lo interesante y la motivación de los mismos nace desde la complejidad de la naturaleza: componentes que interactúan en un sitio mediante relaciones simples (un químico reaccionando con otro, una célula devorando/ayudando a otra, un planeta que atrae/repele a otro) pero que al presentarse en gran número muestran comportamientos que sobrepasan lo que podría esperarse (reacciones autocatalíticas, sistema inmunológico y mareas).

Entre los modelos desarrollados que utilizan AC para representar el movimiento peatonal se encuentran [6] y [7], lo que sumado a su sencillez (base para representar sistemas complejos) indican, uno su eficacia y dos su fácil implementación.

Este trabajo toma como objeto de reflexión un modelo de AC para simular la multitud dentro una estación de TM, que aborda diferentes aspectos que por su naturaleza no son abordados acá, más que por una mera descripción de los mismos: descripción del estado del arte, representación, diseño e implementación del modelo y algoritmia y tecnicidades de implementación y experimentación. Una descripción del diseño de la algoritmia y estructuras computacionales descritos se encuentra en [8]; mientras que la explicación detallada, junto con los experimentos y resultados del simulador se documentaron en [3].

Ya que se tiene el objeto de reflexión identificado, se continua con observar el trabajo llevado a cabo con los AC, que incluye una descripción de los mismos y del modelo revisado junto con una disertación de sus características ante la realidad de la situación. Para luego continuar con los aspectos idiosincráticos más relevantes que hacen parte de la realidad y no son tenidos en cuenta en el modelo del estudio desarrollado, pero que a manera de reflexión sobresalen.

3. Autómatas Celulares

Los AC son una herramienta computacional para representar sistemas complejos, basta con ver el gran número de trabajos realizados, por citar pocos de ellos [5, 9–11]. Se componen de un arreglo de celdas (generalmente rectangular) cuyos estados evolucionan acorde a un conjunto de reglas simples que consideran los estados de sus vecindades.

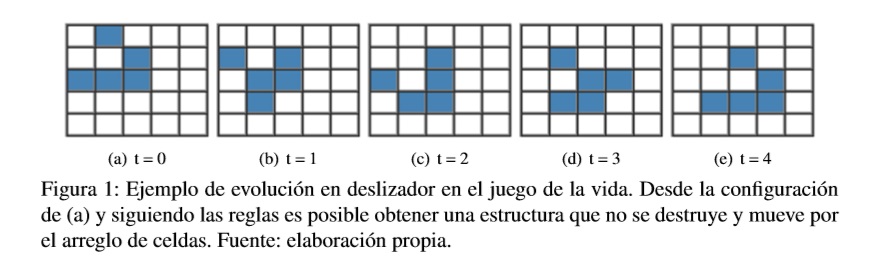
De aquí surgen comportamientos a escalas superiores, basta con ver uno de los ejemplos más sencillos de todos: El juego de la vida [11]. Este AC consta de cuatro reglas que asemejan la vida descritas a continuación, lo notable es ver cómo desde algunas configuraciones iniciales especiales se observan comportamientos a escalas superiores y en ningún momento configurados (ver Figura 1).

Regla 1. Una celda ocupada con menos de dos vecinos muere por soledad.

Regla 2. Una celda ocupada con cuatro o más vecinos muere por sobrepoblación.

Regla 3. Una celda ocupada con dos o tres vecinos sobrevive.

Regla 4. Una celda vacía con tres vecinos revive.

Para el caso del modelo en cuestión, el fenómeno de interés es la ocupación, y en particular el congestionamiento de las estaciones de TM, que se considera un comportamiento global que emerge del comportamiento individual de los pasajeros, por lo cual las reglas deben estar asociadas a sus movimientos.

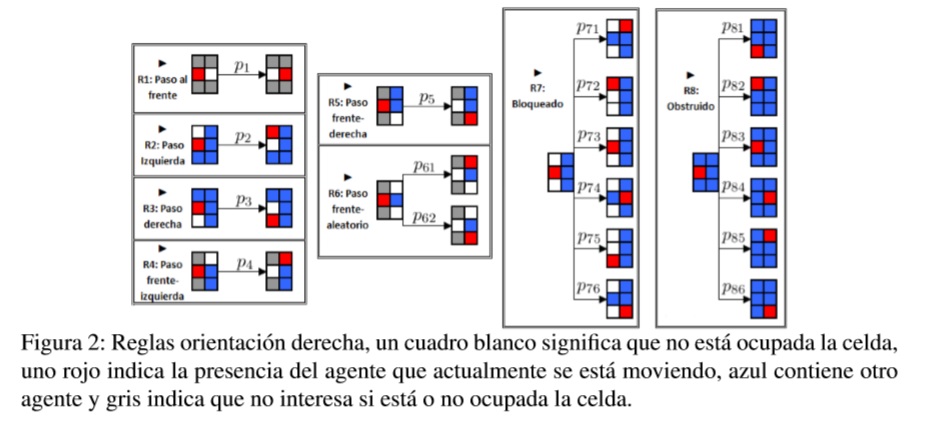
El modelo considera cinco posibles orientaciones: arriba, izquierda, derecha, abajo y quieto, que definen la tendencia hacia donde se mueven las personas. Ya con esto se forma un conjunto de reglas, replicadas por cada una de las orientaciones (la Figura 2 lo muestra para la derecha) que toman la esencia del movimiento de las personas dentro de una estación: si no tiene nadie al frente de un paso en esa dirección (regla 1), si solo puede moverse hacia su izquierda, derecha, izquierda-frente o derecha-frente (exclusivamente) realice ese movimiento (reglas 2, 3, 4 y 5), si se encuentra con alguien al frente y hay espacios, muévase hacia izquierdafrente o derecha-frente (regla 6) y dos reglas más que permiten el movimiento al inicio o dentro de un congestionamiento, que es cuando toda la parte delantera o delantera-lados se encuentra bloqueada (reglas 7 y 8) (ver Figura 2). Existen dos cuestiones a tener en cuenta: la aplicación de estas reglas es estocástica, lo que agrega ese componente humano de indecisión e incertidumbre y la determinación de estos parámetros aleatorios para llevar el modelo lo más cerca a la realidad.

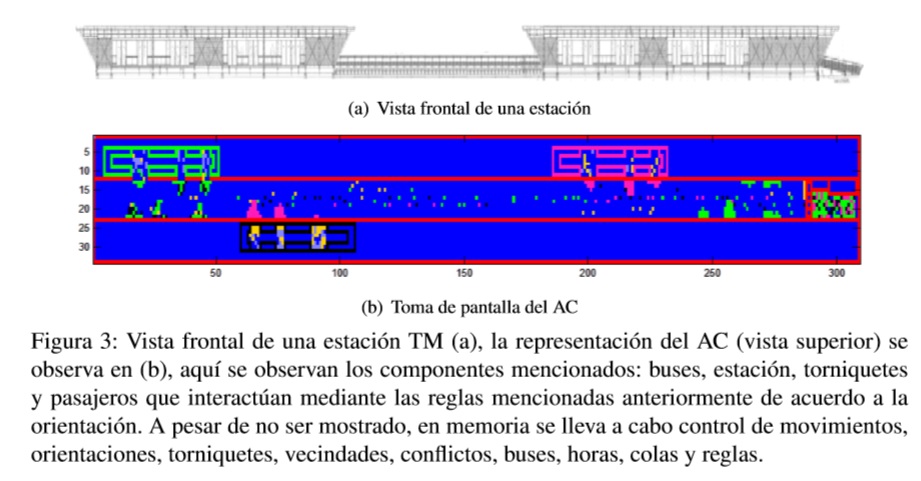
Un ejemplo de la evolución del AC mencionado a partir de una configuración inicial de una estación vacía en el t=0, se puede apreciar en la Figura 3(b) en el t=4000. Se tienen en cuenta parámetros como promedio de llegada de buses y personas en una hora, ocupación de los buses, tiempos de espera y otros configurados previamente y dividos por horas de mayores congestiones. Existe un recuadro (12:23,1:307) en el centro del AC que representa la estación donde los puntos y algunas conglomeraciones de los mismos muestran pasajeros y tumultos, en la parte derecha una concentración intentando ingresar a la estación y a los lados de arriba y abajo de este recuadro tres buses abordando pasajeros.

Una vez capturada la naturaleza del movimiento de personas, permanecen aún fuera de contexto temas como la llegada y partida de buses y de pasajeros, la resolución de conflictos, los cambios de orientaciones, la situación en torniquetes y la detención de pasajeros (tanto dentro de los buses como al momento de esperarlos) los cuales se detallan a continuación.

Para la entrada de pasajeros se selecciona aleatoriamente un pasajero (o bus) cuando su tiempo de llegada, calculado mediante una distribución de Poisson, llega a cero, momento en el cual es colocado en una cola FIFO para luego determinar si existe espacio y ser puesto dentro de la cuadrícula del AC, mientras que la salida para los pasajeros es determinada por la posición del agente o cuando culminan el ciclo llegada-apertura de puertas-abordaje-salida para los buses. La resolución de conflictos se presenta cuando dos o más agentes desean ir hacia la misma celda vacía, para esto primero se determina quién quiere ir a dónde y con esto elegir aleatoriamente uno para su posterior movimiento real . Los cambios de orientaciones se realizan mediante ciertas secciones designadas dentro de la cuadrícula del AC que re-orientan el agente de acuerdo a condiciones específicas e.g., un agente saliendo (orientación arriba o abajo) de un bus al llegar a determinada fila su orientación cambia para que pueda salir (orientación derecha) o un agente se detiene en cierta franja porque está esperando a su bus. En cuanto a los torniquetes son manejados como servidores que atienden a un único agente para moverlo de un lado para otro (interno-externo o viceversa) y ha de controlarse quién es atendido.

Durante el desarrollo del modelo, los autores evidenciaron desafíos académicos que tuvieron que ser solventados, y que implicaron combinar diversos enfoques y técnicas. A continuación se presentan las principales lecciones aprendidas durante dicho proceso, y se discuten a manera de reflexión para los interesados en abordar este tipo de estudios aplicados a situaciones complejas de nuestra realidad.

Sencillez. “El todo es más que la suma de las partes” reza una gran máxima que representa a los AC (y en general a todos los sistemas). De agentes moviéndose regidos por reglas dentro de una cuadrícula emergen dinámicas globales, para el caso, formación de líneas, congestionamientos y oscilaciones son observadas en la ejecución del AC.

Reglas. Dan las normas que definen los nuevos estados del AC, son a los sistemas lo que las relaciones entre los componentes determinan, quizás constituyen, junto con la definición de los estados de las celdas, el aspecto más álgido de su modelamiento. Junto a esto, las reglas son las que posibilitan la emergencia de comportamientos globales, característica que hace robustos los AC; asimismo es importante conocer los posibles casos de reglas factibles, ya que por ejemplo depende de la orientación de los agentes el conjunto de reglas aplicado.

Vecindad. De acuerdo al estado de cada una de las celdas alrededor de una ocupada depende su transición al estado en el siguiente paso de tiempo (vale resaltar que la evolución ocurre precisamente en pasos discretos de tiempo celular). Aquí un aspecto a tener en cuenta, ya que depende del autor el número de vecinos y su distancia al origen para determinar el número de reglas y la forma de las mismas. Este componente se homologa con los sentidos, en especial la visión, ya que de acuerdo a esto las personas toman decisiones para cambiar diferentes comportamientos que determinan su rumbo, velocidad y aceleración. Para el caso se determina la vecindad como el conjunto de los ocho vecinos contiguos en cada posible dirección.

Espacios. De la cuadrícula discretizada se obtienen espacios de dimensiones fijas que representan las celdas del espacio del AC y solamente pueden estar ocupadas por uno y sólo un agente a la vez. Pero el hecho que una madre lleve a su pequeño hijo, una pareja camine tomada de la mano o un simple estudiante que carga una maleta estorbosa, lleva a la modificación dinámica del espacio ocupado por cada uno, lo que sin duda altera y modifica la configuración.

Compresión. Continuando con la idea del anterior item, pero observándola desde un punto de vista diferente: así como no es posible que un agente ocupe un espacio mayor, no lo es que ocupe un espacio menor. Y esto es lo que sucede a la hora de esperar un bus, a medida que pasa el tiempo y con la llegada de buses diferentes a los que espera la gran mayoría, el espacio personal se ve disminuido por dos razones: la llegada de nuevos pasajeros y la expectación de los pasajeros por subirse en un bus, lo que genera la disminución del espacio personal de cada uno. De hecho, un observador desprevenido, podría asegurar que en las horas pico en el sistema real, la aglomeración es tal que pareciera que mas de una persona ocupase el mismo espacio al mismo tiempo.

Conflictos. Aunque la suposición es que dos personas (agentes) no pueden ocupar la misma celda en el mismo instante de tiempo, la aplicación de las reglas de manera simultánea da origen a conflictos de personas intentando ocupar la misma posición. Las reglas no son aplicadas inmediatamente, ya que dependería del orden de la aplicación de las mismas que uno de dos agentes que desean ir al mismo lugar sea preferente. Lo que es realizado es la determinación de pretendientes hacia una celda para su posterior elección aleatoria de uno de ellos. Y aquí surge un dilema: ¿qué tanto la personalidad agresiva o pasiva de una persona hace que no sea aleatorio este movimiento hacia un espacio vacío?

Sincronización. La teoría dicta que la sincronización de cada una de las celdas dentro de un AC ha de realizarse armónicamente. Esta cuestión dicta profundos inconvenientes ya que a pesar de contar con procesadores que ejecutan millones de tareas por segundo y contar con unos cuantos procesadores, no logran una simultaneidad pura.

Es por esto que el AC se ejecuta con cierto orden: izquierda derecha, arriba abajo, combinado, realmente no interesa, la cuestión es bloquear de alguna manera las celdas que ya se han actualizado para evitar una posible inconsistencia con las leyes de la física, que el modelo debe respetar: una propagación incontrolable que no conserva la materia .

Adaptabilidad. Así como es posible utilizar el modelo para simular la situación de congestión, es factible su uso para simular situaciones de evacuación. El resultado obtenido: el tiempo que las personas se demoran en pasar por el torniquete influye así como la apertura de todas las puertas para un mejor tiempo de evacuación. Lo interesante de esto es la posibilidad de simular ese tipo de situaciones y producir estrategias que pudiesen ser implementados para disminuir el daño causado por las mismas.

4. Idiosincrasia

Aspectos como la sincronización, espacio y velocidad son propios de los AC y son el grueso del diseño del modelo. Sin embargo, a continuación se discuten aspectos del sistema real, de tipo idiosincrático, que escapan a las características estándar consideradas por los AC. Cabe aclarar que algunos de estos comportamientos son propios de la cultura bogotana, en otras ciudades o países pueden verse aumentadas o disminuidas, o incluso no verse, pero que escapan del ámbito del AC, y que constituye una de sus limitaciones y que originan los cuestionamientos acerca de cómo abordarlos desde una perspectiva ingenieril, sistémica, sociológica, en últimas, científica.

Colados. Son aquellas personas que por diversas razones entran a la estación por lugares no autorizados, como las puertas de embarque y desembarque hacia y desde los buses. Si bien son pocos comparados con todos los que entran por las puertas, la constante periodicidad en algunas estaciones puede llegar a convertirse en un aspecto de consideración.

Transbordos. No siempre un usuario llega a su destino en un solo bus, de acuerdo a la distribución de rutas por todo el sistema, o por velocidad, se hace necesario tomar dos o más buses de diferentes rutas, en la estación donde se realiza este cambio se observa un agente ir de una puerta a otra.

Libre albedrío. Las diferentes acciones repentinas de las personas: no esperar frente a la puerta, detenerse repentinamente, devolverse, cambiar de carril, protestar, empujar y otras, adiciona en diferentes momentos y de distintas maneras aleatoriedad al comportamiento común que el conjunto de reglas establece. Son estas piezas las que precisamente producen el comportamiento complejo e inesperado en la situación real, por lo que si se desea reducir la brecha modelo-realidad es necesario abordarlas de alguna manera.

Infraestructura de las estaciones. Puertas abiertas, lentas en abrir, sin abrir, rotas, torniquetes dañados y en general cualquier daño físico que se presenta en la estación. Algunos afectando ligeramente (una puerta lenta en cerrar) y otros seriamente (un torniquete dañado). En la realidad se minimiza su frecuencia y tiempo en corrección, aun así y como todo, ha de tenerse en cuenta.

Situaciones de evacuación. En el modelo se simulan situaciones de pánico ideales donde no se tienen en cuenta factores emergentes como la agresividad, velocidad de reacción y angustia generada, lo que repercute en los resultados.

5. Conclusiones

Cuando de investigar con sistemas complejos se trata es necesario realizar una aproximación desde dos puntos distintos: uno holístico determinando las reglas de comportamiento del sistema para emerger comportamientos globales, y uno determinístico que permita tratar temas puntuales de la realidad, por medio de diversos medios clásicos como estructuras de datos, probabilidades, álgebra y algoritmia con el fin de intentar abordar todos los aspectos del sistema que acerquen el modelo a la realidad. Se observa cómo es necesario un punto intermedio entre la ingeniería de sistemas complejos y la clásica, unir lo mejor de los mundos y encontrar oportunidades en falencias del otro agrega una riqueza exquisita en el tema.

En este artículo se han discutido las ventajas y limitaciones del modelo AC para simular la realidad de una estación TM. Estas reflexiones responden a características no tenidas en cuenta ni descritas en documentación alguna ya que surgen de la adaptación de un modelo teórico a una situación actual, así como de aspectos sociales de la cultura que no encuentran su representación en los conceptos teóricos. Su análisis profundo e implementación requiere del enfoque mencionado anteriormente para detallar y tratar cada uno de los aspectos mencionados.

Referencias

1. Hoekstra, A., Kroc, J., and Sloot, P. Introduction to modeling of complex systems using cellular automata. In Simulating Complex Systems by Cellular Automata, Understanding Complex Systems, pages 1–16. Springer Berlin Heidelberg, 2010.
   
2. Mina, A., Braha, D., and Bar-Yam, Y. Complex engineered systems: A new paradigm. In Dan Braha, Ali A. Minai, and Yaneer Bar-Yam, editors, Complex Engineered Systems, Understanding Complex Systems, pages 1–21. Springer Berlin Heidelberg, 2006.
   
3. Rodríguez-Garzón, C.A. Dinámica de (des)congestionamiento de estaciones TransMilenio mediante Autómatas Celulares Discretos. Trabajo de Grado (Ingeniero de Sistemas). Universidad Distrital Francisco José de Caldas. 2014.
   
4. Rojas-Galeano, S.A. Paradigmas alternativos de computación: paralelismo y simplicidad inspirados en la biología. Ingeniería, 5(1), 1999.
   
5. Ilachinski, A. Cellular Automata: A Discrete Universe. World Scientific Pub Co Inc, reprint edition, July 2001.
   
6. Burstedde, C., Klauck, K., Schadschneider, A., and J. Zittartz. Simulation of pedestrian dynamics using a two-dimensional cellular automaton. Physica A: Statistical Mechanics and its Applications, 295(3-4):507–525, June 2001.
   
7. Kirchner, A. and Schadschneider, A. Simulation of evacuation processes using a bionicsinspired cellular automaton model for pedestrian dynamics. Physica A: Statistical Mechanics and its Applications, 312(1-2):260–276, September 2002.
   
8. Rojas-Galeano, S.A. and Rodríguez-Garzón, C.A. A discrete model of transmilenio station occupation: Representation and algorithms. Revista de Ingeniería Universidad de los Andes, page 27–32, August 2014.
   
9. Neumann, J. and Burks, A.W. Theory of Self-Reproducing Automata. University of Illinois Press, 1966.
   
10. Hoekstra, A., Kroc, J., and Sloot, P. Simulating Complex Systems by Cellular Automata. Springer, 2010.
    
11. Gardner, M. The fantastic combinations of john conway’s new solitaire game of life. Scientific American, 223(4):120–123, 1970.

Camilo Alfonso Rodríguez Garzón

Ingeniero de sistemas de la Universidad Distrital Francisco José de Caldas, Bogotá, Colombia, interesado en autómatas celulares, lógica difusa, redes neuronales, virtualización y seguridad de la información, actualmente cursando una maestría en Seguridad de la Información, correo electrónico: camilo.18.20@gmail.com

Systems Engineer from the Universidad Distrital Francisco José de Caldas, Bogotá, Colombia, interested in cellular automata, fuzzy logic, neural networks, virtualization and information security. He is currently enrolled in a MSc. degree in information security.

e-mail: camilo.18.20@gmail.com

Este trabajo está autorizado por una Licencia AttributionNonCommercialNoDerivs CC BYNC-ND.