Ciencia, Investigación, Academia y Desarrollo

Ingeniería, 2006-00-00 vol:11 nro:2 pág:61-69

Modelo de Semaforización Inteligente para la Ciudad de Bogotá

Intelligent model traffic light for the city of Bogota

Octavio Salcedo

Director del Grupo de Investigación "Internet Inteligente" Universidad Distrital. Profesor, Facultad de Ingeniería, Universidad Distrital.

Luis Fernando Pedraza

M.Sc. en Teleinformática, Universidad Distrital.

César Augusto Hernández

M.Sc. en Teleinformática, Universidad Distrital.

Resumen

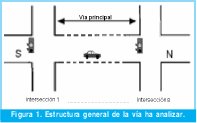
En este articulo se presenta el diseño de un modelo de tráfico vehicular, el cual examina el trafico existente en una vía principal de Bogotá a través de una serie de semáforos, y a partir de esto se sincroniza el tiempo de duración y de desfase de los semáforos, utilizando para ello el Sistema de Inferencia Difusa Basado en Redes Adaptativas e intentando mantener a su vez la velocidad máxima de los vehículos permitida en la vía (Figura 1). El modelo es simulado en el software Matlab y se evalúan los resultados a nivel macroscópico con el modelo de temporización fija que funciona actualmente en Bogotá.

Palabras clave: Parámetros Macroscópicos, Temporización Fija, Tráfico Vehicular, Redes Adaptativas, Reglas Difusas, Suma Del Error Al Cuadrado.

Abstract

This article details the design of a traffic system model for vehicles, which examines the traffic traveling through a series traffic lights on a main road in Bogota. The Adaptive Network Based Fuzzy Inference Systems is used to synchronize the time of duration and phase angle of the traffic lights, and also tries to maintain the maximum possible velocity of the vehicles traveling on the road (Figure 1). The model is simulated in Matlab software and the results are evaluated at macroscopic level with the fixed time model currently operating in Bogota.

Key words: Macroscopic Parameters, Fixed Time, Vehicle Traffic, Adaptive Networks, Rules Fuzzy, Sum Of Squared Error.

1. INTRODUCCIÓN

A lo largo de la historia de Bogota D.C, el flujo vehicular se ha ido incrementando constantemente, mientras que los recursos proporcionados para el desarrollo de la infraestructura vial han sido limitados, esto se ha reflejado en situaciones donde el volumen de transito en uno o mas puntos de una vía excede el volumen máximo que puede pasar por ellos. Por lo tanto, el control de tráfico inteligente se convertirá en una herramienta muy importante en el futuro, para controlar la congestión vehicular y beneficiar así, la calidad de vida de las personas, el medio ambiente y la economía de la ciudad.

El transporte particular que se mueve por la red vial de Bogotá consta aproximadamente de 670.000 automóviles matriculados, los cuales manejan solo un 20% de los viajes diarios en la ciudad. Existen en la actualidad 21.500 buses, busetas y microbuses. Estos vehículos realizan el 60% de los viajes en la ciudad y el restante 20% esta cubierto por el sistema de Transmilenio. "Si el parque automotor creciera a una tasa del 4% anual (como en los últimos años), se calcula que para el 2015 Bogotá tendría aproximadamente 1´170.000 vehículos, y si creciera al 7% anual habría 1´800.000 vehículos" [1]. Este crecimiento inminente ha llevado y llevará a grandes congestiones vehiculares, que hoy por hoy son uno de los problemas más grandes de la capital del país, trayendo como consecuencia la necesidad de un óptimo sistema de control que permita un ágil desplazamiento y que reduzca entre otras el alto consumo de combustibles, la alta contaminación ambiental causada por el desprendimiento de monóxidos propio de los automotores y el nivel de accidentalidad.

En los últimos años el paradigma de control del flujo vehicular mediante la programación de los semáforos ha presentado múltiples variaciones que van desde la programación con tiempos fijos en las diferentes fases de los semáforos hasta la coordinación de grupos desde una central computarizada, lo que demuestra que se han obtenido grandes avances en el tema, por ejemplo en [2] se describe un controlador de lógica difusa para una sola intersección, en [3] se estudia el uso de la lógica difusa para el control de intersecciones múltiples, en [4] se describe una red de caminos conectados por semáforos basados en sistemas expertos, en [5] se presenta un controlador de semáforos usando un predictor simple basado en optimización, en [6] se desarrolla un controlador de tráfico vehicular basado en algoritmos evolutivos, en [7] se presenta un método de control de semáforos basado en aprendizaje reforzado, el cual en [8] utiliza un valor basado en la función del semáforo a partir de una red neuronal y en [9] se uso la función basada en vehículos. Esto demuestra que se ha desarrollado un gran número de soluciones, pero a su vez existe un gran campo de trabajo, como lo es el modelo presentado en este trabajo para optimizar el tiempo de sincronismo de los semáforos.

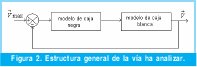
Por lo tanto, la intención de este artículo es dar un enfoque en el manejo de la semaforización en Bogotá de acuerdo a los requerimientos de transito en una vía, basado en técnicas de control inteligente como lo es el Sistema de Inferencia Difusa Basado en Redes Adaptativas (ANFIS), el cual ha demostrado una gran adaptabilidad y capacidad para toma de decisiones en sistemas con fluctuaciones como lo es el tráfico [10], para ello se usa una robusta implementación que varia una expresión matemática. Dicho de otra forma el objetivo es controlar un modelo de caja blanca (expresión matemática), con un modelo de caja negra (ANFIS), como se observa en la figura 2.

2. DISEÑO DEL CONTROLADOR DE TRÁFICO

Inicialmente se presenta un modelo de tráfico macroscópico, el cual es el punto de partida para diseñar el control de los tiempos de verde de los semáforos y los respectivos desfases entre estos, para lo que es usado el ANFIS.

2.1. Descripción del modelo

En [11], se introduce un modelo microscópico de tráfico vehicular, prácticamente es un modelo ideal basado en el comportamiento cinemático de un solo vehículo que viaja a través de una secuencia de semáforos que encienden y apagan con una frecuencia específica y que presentan distancias fijas (para este caso 100 mts).

Por lo tanto partiendo de este artículo, el primer objetivo es analizar una corriente vehicular (varios vehículos) a través de una secuencia de semáforos que pueda presentar distancias variables entre ellos, y luego controlar estos semáforos para pretender mantener la velocidad máxima de la corriente vehicular permitida en la vía.

A continuación se describe los parámetros que componen a la función:

La separación entre el n-ésimo y el (n+1)-ésimo semáforo es Ln. La n-ésima luz es verde si sen(ωnt +φn) > 0 y roja en caso contrario, donde ωn es la frecuencia del semáforo, y φn es el desfase entre semáforos. Un automóvil en esta secuencia de semáforos puede tener:

• Una aceleración positiva a+ hasta que su velocidad alcanza la velocidad máxima de la vía (vmáx),


• Una velocidad constante vmáx con aceleración nula,


• Una aceleración negativa -a- hasta que se detiene.

En la ecuación (1), θ(v) es la función escalón unitario, la cual impide que el modelo arroje velocidades superiores a la máxima e inferiores a cero.

Como el auto se acerca al n-ésimo semáforo con velocidad v el conductor debe tomar una decisión frenar o no en la distancia Xc:

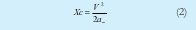
La diferencia entre Ln y Xc (Ln-Xc), es la distancia a la cual el vehículo puede acelerar hasta alcanzar la vmax.

Para el modelo macroscópico en el que se maneja un flujo vehicular, cada vehículo acelera con una aceleración a₊, se supone que el primer vehículo en la fila posee una a₊=2,32m/s² y que cada vehículo que lo precede disminuye su a₊ en un 2%, y se evalúa en cada Δ la diferencia entre X y Xc (X es la distancia recorrida por el vehículo), cuando esta sea menor a 1m, se analiza el estado del semáforo, es decir sen(ωnt + φn), si el resultado es positivo se continua con a₊ y por el contrario se actualiza el valor de aceleración a a_-, que en este caso es de -3,9m/s². De esta forma se calculan los datos de velocidad instantánea con los cuales se obtienen los datos de la velocidad promedio para los m autos del flujo vehicular.

La velocidad v de la ecuación (1), se reemplaza por el promedio de la velocidad promedio de los m vehículos (Vt):

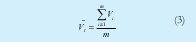
Donde V_i es la velocidad promedio del m-ésimo vehículo. Esta velocidad promedio se halla a partir de la velocidad instantánea del vehículo (V_in), la cual se calcula cada 0.1segundos (Δt), mientras el vehículo se desplaza en el flujo vehicular del semáforo n hasta el n+1.
Donde:

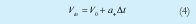
En este caso V₀ es la velocidad que lleva el vehículo en el intervalo de tiempo.

Luego de describir el modelo a utilizar para caracterizar el flujo de vehículos a través de una vía, se utiliza la ecuación (5) para sincronizar el tiempo de verde (t_v) y el tiempo de desfase (t_d), de los semáforos con el modelo ANFIS:

Donde,
t_vn es el tiempo de verde del n-ésimo semáforo.
t_An es el tiempo de amarillo del n-ésimo semáforo.
t_Rn es el tiempo de rojo del n-ésimo semáforo.
t_RAn es el tiempo de rojo-amarillo del n-ésimo semáforo.
t_dn es el tiempo de desfase de la luz verde entre el n-ésimo semáforo y el (n-1)-ésimo semáforo.

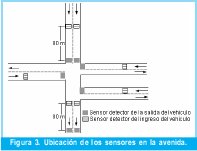
Además, se debe tener en cuenta las restricciones utilizadas en este modelo, las cuales consisten en tener un número máximo de 20 vehículos en un carril partiendo del reposo; pero en su gran mayoría las avenidas de Bogotá como la avenida Caracas, sobre la cual se va ha realizar el análisis del modelo tiene dos carriles en cada sentido, como se ve en la figura 3, por lo que se ubican sensores de bucle magnético a 80 mts de distancia con respecto al semáforo y a ambos lados de la vía para lograr una detección de un numero máximo de aproximadamente 40 vehículos. Para esto se tiene en cuenta que la longitud promedio del vehículo es de 4 mts y la separación entre vehículos se encuentra a partir del modelo lineal planteado en [12], [13], [14], partiendo de la información dada en [15] en donde el volumen máximo vehicular (q_m) que se presenta sobre la avenida Caracas, es de alrededor de 2736 vehículos/hora y como la velocidad máxima (vmáx) de la vía es de 60 km/hora, se tiene que la densidad de congestionamiento vehicular (k_c) es:

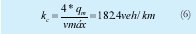
El espaciamiento promedio a flujo máximo (s_m) es:

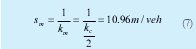
Y la separación entre vehículos a flujo máximo (s_p) es:

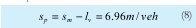
Donde l_v es la longitud promedio del vehículo [12], [16].

2.2. Diseño del controlador

Ahora se procede a diseñar el controlador ANFIS para asignar el tiempo de verde de los semáforos y sus respectivos desfases, buscando obtener la velocidad máxima permitida en la vía, que para este caso es de 16,67 m/s (60 km/h). Este diseño se realiza para controlar el modelo descrito en el ítem anterior.

Para el entrenamiento del modelo neuro-difuso, las reglas difusas del tipo Takagi-Sugeno se representan de la siguiente forma [9]:

Regla n: Si X es A_n y Y es B_n, entonces f_n = p_nX + q_nY + r_n,

En el caso de dos semáforos la arquitectura de las reglas implementadas es:

Regla 1: Si X es A₁ y Y es B₁, entonces f₁ = p₁X + q₁Y + r₁,

Regla 2: Si X es A₂ y Y es B₂, entonces f₂ = p₂X + q₂Y + r₂.

Donde A_n y B_n son los conjuntos difusos de entrada y p_n, q_n y r_n son constantes, para este caso pn y qn son cero obteniendo un modelo Takagi-Sugeno de orden cero. Los niveles de activación de las reglas se calculan como:

Donde el operador lógico and (.) es modelado por una t-norma continua (producto). Las salidas individuales de cada regla son obtenidas como una combinación lineal entre los parámetros del antecedente de cada regla: f_n = p_nX + q_nY + r_n, n=1,2,.... La salida de control del modelo f se obtiene por la normalización de los grados de activación de las reglas por la salida individual de cada regla:

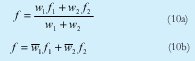
w₁ y w₂ son los valores normalizados de w₁ y w₂ con respecto a la suma (w₁ + w₂). La red neuronal híbrida que representa este tipo de inferencia es una red adaptativa con cinco capas, donde cada capa representa una operación del mecanismo de inferencia difuso. Esta red se muestra en la figura 4.

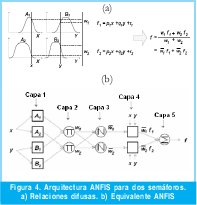
Por lo tanto, X es el antecedente (universo de entrada) tiempo de verde (t_v), Y es el antecedente (universo de entrada) tiempo de desfase (t_d) de la ecuación (5), y f corresponde al consecuente (universo de salida) velocidad promedio del flujo vehicular (V_t), dada en la ecuación (3). El modelo implementado en el software Matlab es mostrado en la figura 5.

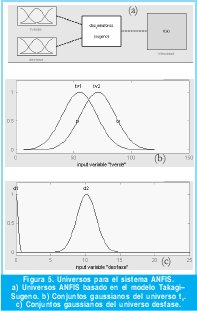
En este caso se utiliza conjuntos de entrada gaussianos, los cuales están definidos por:

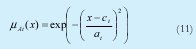
Donde el parámetro C_i es el valor medio del conjunto, y ai es el coeficiente de dispersión. En este caso C_i indica el tiempo de verde y el desfase necesarios para ajustar el modelo, como se muestra en la figura 5 b) y c). A continuación se muestra la forma en que se entrenan los parámetros, para asignar el tiempo de verde y el desfase con el fin de alcanzar la velocidad máxima.

2.2.1 Aprendizaje del modelo

El modelo ANFIS tiene dos tipos de parámetros que deben ser entrenados:

1. Los parámetros de los antecedentes (t_v y desfase), para lo cual se encuentran las constantes que caracterizan los conjuntos gaussianos, para este caso el t_vn y el desfase, son el resultado del centro del conjunto.
2. Los parámetros del consecuente (V_T). Estos son parámetros lineales de la salida del modelo de inferencia.

El paradigma de aprendizaje del modelo ANFIS emplea algoritmos de gradiente descendente para optimizar los parámetros del t_v y el desfase y el algoritmo de mínimos cuadrados para determinar los parámetros lineales del V_T. A esta combinación se lo conoce como regla de aprendizaje híbrido, la cual es usada en el aprendizaje de este modelo [18].

Ahora se aplica lo descrito en [18] y [19], en donde para aplicar el aprendizaje híbrido en grupo, en cada periodo de entrenamiento debe ejecutarse un paso hacia adelante y un paso hacia atrás. En el paso hacia adelante, los parámetros de las funciones de los conjuntos son inicializados y se presenta un vector de entrada-salida, se calculan las salidas del nodo para cada capa de la red y entonces los parámetros de la V_T son calculados usando el método de mínimos cuadrados. Una vez identificados los parámetros de la V_T, el error es calculado como la diferencia entre la salida de la red y la salida deseada presentada en los pares de entrenamiento. En este caso se usa una de las medidas más empleadas para calcular el error de entrenamiento, el cual es la suma del error al cuadrado (SEC), definido como:

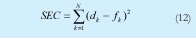
Los d_k corresponden a los patrones de entrenamiento proporcionados (salidas deseadas) y f_k es la correspondiente salida de la red. En el paso hacia atrás, las señales de error son propagadas desde la salida, en dirección de las entradas y el vector gradiente es acumulado para cada dato de entrenamiento. Al final del paso hacia atrás para todos los datos de entrenamiento, los parámetros en la capa 1 (parámetros de los conjuntos) son actualizados por el método descendente en una magnitud Δα igual a:

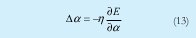
Donde E es el error de salida y es la velocidad de aprendizaje que puede ser expresada como:

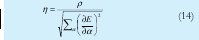
Aquí ρ es el tamaño del paso, o sea la longitud de cada transición a lo largo de la dirección del gradiente en el espacio de parámetros. Generalmente, se puede cambiar el valor de ρ para variar la velocidad de convergencia de la siguiente manera:

Se observa que si ρ es pequeño, el método del gradiente aproxima de cerca la trayectoria del gradiente, pero la convergencia será lenta puesto que el gradiente se debe calcular muchas veces. Por otra parte, si ρ es grande, la convergencia será inicialmente muy rápida, pero el algoritmo oscilará sobre el grado óptimo. De acuerdo con estas observaciones, se actualiza ρ según las siguientes reglas heurísticas:

1. Si la medida del error experimenta cuatro reducciones consecutivas, se aumenta en el 10%.


2. Si la medida del error experimenta dos combinaciones consecutivas de un aumento y de una reducción, se disminuye en un 10%.

Sin embargo los valores de cuatro reducciones, dos combinaciones y el aumento o disminución de ρ en el 10%, son elegidos de manera un poco arbitraria, aunque como se observa mas adelante, muestran un buen resultado en la respuesta de la V_T, lo importante es no escoger un valor inicial de muy grande, para que este no sea critico [20].

3. VALIDACIÓN DEL MODELO

Para la validación del modelo se utiliza la Av. Caracas de Bogotá D.C, desde el cruce de la calle 36 hasta el cruce de la calle 51 (en total ocho cruces) en sentido sur a norte, para lo cual se valida el modelo propuesto confrontándolo con el de tiempos fijos coordinado por la Secretaria de Movilidad de Bogotá. Las características actuales de estos cruces, como lo son distancia entre cruces y tiempos de semáforos se presentan en la Tabla I, donde se observa que los primeros cuatro cruces tienen un tiempo promedio de ciclo (tiempo de rojo más tiempo de verde), de 96 segundos y para los cuatro cruces siguientes este tiempo es de aproximadamente 115 segundos. Los tiempos de Rojo-Amarillo y Amarillo para los semáforos de los cruces son de un segundo y dos segundos respectivamente.

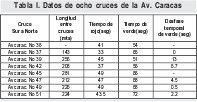
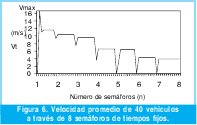
Las graficas de velocidad promedio de los vehículos a través de los ochos semáforos para el modelo de temporización fija y el modelo propuesto, se realizan para una cantidad de 40 vehículos. En la figura 6 se grafica el modelo de temporización fija para los tiempos y distancias dados en la Tabla I, allí se ve que el sistema presenta un comportamiento caótico para un volumen apreciable de vehículos, esto conlleva a que la velocidad promedio sea de 6,9 m/s.

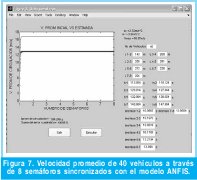
En la figura 7, se observa los tiempos de verde (tv_n) y el desfase entre cada uno de los semáforos devueltos por el modelo ANFIS y además se muestra en color azul la velocidad promedio del flujo vehicular que se desea alcanzar (en este caso 16,67 m/s) y en color verde la velocidad promedio que realmente se alcanza con los tiempos y desfases de los semáforos proporcionados por el modelo, aquí la velocidad promedio es de 12,77 m/s. A su vez se muestra el tiempo promedio de circulación de los vehículos el cual es aproximadamente 104 segundos y la suma del error al cuadrado es de 10606, dada por el error de entrenamiento de la red neurodifusa a través de 10 periodos. Vale la pena aclarar que en este caso el ciclo total de cada semáforo es de 3 minutos, de los cuales el máximo tiempo que puede ser destinado para verde es de 149 segundos, el mínimo tiempo de rojo es de 28 segundos, el tiempo de rojo-amarillo es de 1 segundo y el de amarillo es de 2 segundos.

3.1 Resultados

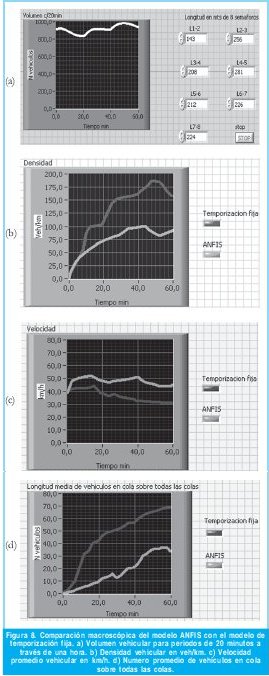
Ahora se procede a realizar una comparación con los parámetros macroscópicos de los dos modelos (ANFIS y temporización fija), para esto se parte de lo planteado en [15] en donde el volumen vehicular máximo que se presenta sobre la avenida Caracas, es de alrededor de 2736 vehículos/hora. Tomando como referencia el volumen anteriormente mencionado, se realiza una tabulación de este, en periodos de 20 minutos durante una hora, como se muestra en la figura 8 a). Esto es realizado a través de los ocho semáforos de la Av. Caracas descritos en la tabla I, los cuales actualmente se encuentran con tiempos fijos y estos son comparados con los tiempos arrojados por el modelo ANFIS diseñado en el capitulo anterior. En la figura 8 b) se observa la densidad vehicular, en la c) la velocidad promedio máxima alcanzada por los vehículos y en la d) la longitud promedio de vehículos en cola sobre las ocho colas, para cada uno de los modelos en discusión.

4. ANÁLISIS DE RESULTADOS

Al comparar la velocidad promedio de los 40 vehículos en los dos modelos, como se muestra en las figuras 6 y 7, puede observarse un comportamiento estable para el modelo ANFIS y una velocidad promedio mayor, aproximadamente un 85% con respecto al modelo de temporización fija.

El controlador diseñado con ANFIS, controla de una mejor manera el tráfico vehicular que el sistema de temporización fija como se presenta en el siguiente análisis: En la figura 8 b) el promedio de densidad vehicular se reduce de 136 vehículos/km a 78 vehículos/km, aproximadamente en un 42.6% con respecto al sistema de temporización fija, en la figura 8 c) la velocidad promedio para el modelo ANFIS es de 48.1 km/h mientras que para la temporización fija es de 36 km/h, en este caso la velocidad aumenta en un 33.3% con el modelo propuesto, y en la figura 8 d) la cantidad promedio de vehículos en cola sobre todas las colas para el sistema de temporización fija es de 48.75 vehículos y para el modelo ANFIS es de 18.65 vehículos, o sea se tiene una reducción con el modelo ANFIS en la cantidad de vehículos en cola de un 61.7%.

5. CONCLUSIONES Y RECOMENDACIONES

Al analizar los resultados de la figura 8, se observa que el control de los semáforos con el modelo ANFIS es más óptimo ya que la densidad vehicular se reduce, permitiendo atender una mayor cantidad de vehículos en una misma distancia al compararse con el sistema de temporización fija. A su vez el modelo ANFIS aumenta la velocidad promedio de los vehículos a través de la vía lo cual aumenta la movilidad vehicular, y también se presenta una disminución del promedio de vehículos en cola sobre todas las colas, reduciendo la posibilidad de generar una congestión vehicular por causa de los semáforos.

Para la obtención de buenos resultados con este modelo, es aconsejable utilizarlo en un sistema progresivo flexible el cual permita sincronizar los semáforos en un sentido u otro, según las horas de máxima demanda vehicular.

La red neurodifusa del modelo ANFIS se entrena durante 10 periodos, con lo que se alcanza un tiempo corto de ejecución. A medida que los periodos de entrenamiento de la red se aumentaron no se observo una mejora significativa en la velocidad de circulación vehicular y en cambio si un aumento significativo en el tiempo de ejecución.

La implementación del modelo propuesto en la ciudad, conllevaría a unos beneficios de índole social entre los que se encuentran:

• El aumento de la calidad de vida de los ciudadanos, puesto que permite a las personas que se transportan en automotores llegar a su destino sin mayores contratiempos y ocupar así el tiempo en otras labores como su familia.


• Disminución del nivel de ruido, ya que los conductores accionarían la bocina con menor frecuencia. A su vez el vehículo disminuiría la expulsión de gases, lo cual representa no solo una reducción en la contaminación ambiental, sino en el consumo de combustible, lo que implica un costo inferior en el sostenimiento del vehículo para el dueño.

Como trabajo futuro se recomienda realizar el modelo teniendo en cuenta que si un volumen grande de vehículos congestiona un cruce anterior, el número de vehículos que viene de ese cruce sea reducido. También es recomendable incluir en el modelo factores que afectan al conductor como lo es el clima, la época del año, entre otros.

REFERENCIAS BIBLIOGRÁFICAS

[1] Fondo de prevención vial, Sistemas de Transporte, Marzo 2007, disponible en http://www.fonprevial.org.co/htm/ htm_docentes/sistema1.htm

[2] K. K. Tan, M. Khalid, y R. Yusof "Intelligent traffic lights control by fuzzy logic". Malaysian Journal of Computer Science, vol. 9-2, 1995.

[3] J.H. Lee, K.M. Lee, K.A. Seong, C.B. Kim, y H. Lee-Kwang "Traffic control of intersection group based on fuzzy logic". Proceedings of the 6th International Fuzzy Systems Association World Congress, 1995, pp. 465-468

[4] N. Findler, y J, Stapp "A distributed approach to optimized control of street traffic signals". Journal of Transportation Engineering, vol. 118-1, 1992, pp 99-110.

[5] K. Tavladakis y N. C. Voulgaris "Development of an autonomous adaptive traffic control system". ESIT '99. The European Symposium on Intelligent Techniques, 1999.

[6] H. Taale, Th. Back, M. Preuß, A. E. Eiben, J. M. de Graaf, y C. A. Schippers "Optimizing traffic light controllers by means of evolutionary algorithms". EUFIT'98, 1998.

[7] T. L. Thorpe y C. Andersson "Traffic light control using sarsa with three state representations" Tech. Rep., IBM corporation, 1996.

[8] T. Thorpe "Vehicle traffic light control using sarsa" M.S. tesis, Department of Computer Science, Colorado State University, 1997.

[9] M.Wiering, J. Vreeken, J. Van Veenen, y A. Koopman "Simulation and optimization of traffic in a city". IEEE Intelligent Vehicles Symposium (IV'04). IEEE, 2004. A system level study. Technical Report 1991-09-01, California PATH, 1991.

[10] H. Hiok y B. Qiu "Fuzzy Logic Target Utilization and Prediction for Traffic Control". Proc. IEEE ICC', 2000, pp. 1644-1648.

[11] B. A Toledo, V. Muñoz, J. Rogan y C. Tenreiro "Modeling traffic through a sequence of traffic lights". Physical Review E, Vol 70, 2004, pp. 0161071-0161076.

[12] R. C. Mayor y J. Cardenas, Ingeniería de Tránsito: Fundamentos y aplicaciones, 7ª edición, Afaomega Grupo Editor, Cal y Mayor y Asociados, México D.F., 2000.

[13] B.D. Greenshield "A Study in Highway Capacity", Highway Research Board, Vol. 14, 1935, pp. 448-477.

[14] N.J. Garber y L.A. Hoel , Traffic and Highway Engineering, 3ra edición, Thomson Learning, 2001.

[15] E. Hurtado y N. L. Torres, "Variables Que Determinan La Localización De Cruces Peatonales En Bogotá", Tesis de Grado, Departamento de Ingeniería Civil, Universidad Nacional, Bogotá D.C, Colombia, 2000.

[16] Secretaría de Movilidad Bogotá D.C, Manual De Planeación Y Diseño Para La Administración Del Tránsito Y El Transporte, Tomo I, Cap 5, pp 5-50 a 5-72, 2005, disponible en www.transitobogota.gov.co

[17] T. Takagi y M. Sugeno "Derivation of fuzzy control rules from human operator's control actions", Proc. Of the IFAC Symp. on Fuzzy Information, Knowledge Representation and Decision Analysis, 1983, pp. 55-60.

[18] J.-S. R.Jang "ANFIS: Adaptive-Network-based Fuzzy Inference Systems", IEEE Transactions on Systems, Man, and Cybernetics, Vol. 23, 1993.

[19] S. Zak, Systems and Control, Oxford University Press, 2003.

[20] Jang J-S. R. "Input Selection for ANFIS Learning", Proceedings of the IEEE International Conference on Fuzzy Systems, New Orleans, 1996.

Octavio Salcedo
Nació en Morroa, (Sucre), Colombia. Es Ingeniero de Sistemas de la Universidad Autónoma de Colombia. Magíster en Teleinformática de la Universidad Distrital. Magíster en Economía (PEG) de la Universidad de los Andes de Bogotá. Estudiante del Doctorado en Ingeniería Informática de la Universidad Pontificia de Salamanca, España. Se desempeña como Docente de la Facultad de Ingeniería de la Universidad Distrital y en la Universidad Nacional de Colombia, Sede Bogotá. Es director del Grupo de Investigación "Internet Inteligente" de la Universidad Distrital Francisco José de Caldas. ojsalcedop@unal.edu.co

Luis Fernando Pedraza Martínez
Nació en Bogotá, Colombia. Es Ingeniero Electrónico de la Universidad Distrital F. J. C. de Bogota, Colombia. Magíster en Ciencias de la Información y las Comunicaciones de la Universidad Distrital. Se desempeñó como Docente en el área de Control en Universidades como Cooperativa de Colombia y Distrital F. J. C, es director del grupo de investigación "Semaforización Inteligente". Actualmente se desempeña como Docente de planta en la Universidad Militar Nueva Granada en las áreas de comunicaciones y control. pedrazaluis2001@yahoo.es

César Augusto Hernández Suárez
Nació en Villavicencio, Colombia. Es Ingeniero Electrónico de la Universidad Distrital F. J. C. de Bogota, Colombia. Especialista en Interconexión de Redes y Servicios Telemáticos de la Universidad Manuela Beltrán. Candidato a Magíster en Ciencias de la Información y las Comunicaciones de la Universidad Distrital.

Se desempeñó como Docente Investigador en la Universidad Manuela Beltrán durante 3 años donde desarrolló varios proyectos aprobados y financiados por Colciencias, dentro de los cuales esta el proyecto Sistema Electrónico Mecánico para la enseñanza de la Lectoescritura del Braille para el cual se encuentra en curso la patente de invención.

Actualmente se desempeña como Docente de planta en la Universidad Distrital en el área de la electrónica digital y el procesamiento digital de señales. lctsubasa@gmail.com