DOI:
https://doi.org/10.14483/23464712.5023Published:
2013-01-01Significados de “matematização” de professores e estudantes de um curso de licenciatura em fisica: um estudo de caso
Meanings of "Mathematization" of teachers and students in a program to educate physics teachers: a case study
Keywords:
Physics teaching, Mathematization, Relation between Maths and Physics teaching, Education for physics teachers. (en).Keywords:
Ensino de Física, Matematização, Relação matemática e ensino da física, Licenciatura em Física (es).Downloads
References
BARDIN, L. Análise de Conteúdo. Edições 70. Lisboa, 2002.
CANTOR, G. N. Berkeley, reid, and the mathematization of mid-eighteenth-century optics. Journal of the History of Ideas, Pennsylvania, v.38, n.3, pp. 429-448, 1977.
ESTRELA, A. Teoria e Prática de Observação de Classes. Editora Porto. Portugal. 4 ed. 1994.
GINGRAS. Y. What did mathematics do to physics? hist. sci., xxxix, 2001.
MARTINS, G. Estudo de Caso, Uma estratégia de Pesquisa. Editora Atlas. São Paulo. 2008.
PATY. M. The idea of quantity at the origin of the legitimacy of mathematization in physics. Constructivism and practice: towards a social and historical epistemology, Rowman & littlefield, Lanham (md.,USA), p. 109-135, 2003.
PIETROCOLA, M. A Matemática como estruturante do conhecimento Físico. Cad.Cat.Ens.Fís. v.19, n.1: p. 88-108, ago. 2002.
UHDEN, O; KARAM, R; PIETROCOLA, M; POSPIECH, G. Modelling Mathematical Reasoning in Physics Education. Science & Education. Volume 21, Number 4. 2012.
How to Cite
APA
ACM
ACS
ABNT
Chicago
Harvard
IEEE
MLA
Turabian
Vancouver
Download Citation
GÓNDOLA
ISSN 2145-4981
Vol 8 No 1 Enero-Julio de 2013.
SIGNIFICADOS DE “MATEMATIZAÇÃO” DE PROFESSORES E ESTUDANTES DE UM CURSO DE LICENCIATURA EM FISICA: UM ESTUDO DE CASO
Meanings of "mathematization" from teachers and students in a program of education physics teachers: A CASE STUDY
Diego Vizcaino1
Eduardo Terrazzan2
1Contato: d_vizcaino@yahoo.com
1Contato: eduterra@pq.cnpq.br
Resumen
Apresenta-se um estudo sobre a forma como é entendida e trabalhada a Matemática no âmbito do Ensino e a Aprendizagem da Física, no curso de Licenciatura em Física de uma Universidade pública do interior de São Paulo, Brasil. Para tal, fizemos um levantamento sobre as propostas de pesquisadores nesta linha, que mostrou-nos como vêm-se inserindo neste campo o termo de Matematização” para representar processos por meio dos quais o aprendizado da Física ganha significação, ao considerar a formação de habilidades, tais como; observação, descrição, idealização, analise lógico local, axiomatização e aplicação. Acompanhamos durante um ano, diversas disciplinas de Física de diferentes semestres buscando que fossem do começo, metade e final do curso. Utilizamos o diário de campo como técnica de registro da informação, coletando; dados básicos, conteúdos, e desenvolvimento da aula. Com base na análise do diário de campo foi elaborado um roteiro de observação contendo indicadores que permitissem detectar a presença e a forma como se desenvolvem processos de Matematização, servindo-nos deste roteiro, observamos durante um semestre um outro grupo de disciplinas de Física, fazendo uma analise de conteúdo sobre o material produzido. Constatamos que o fato de observar disciplinas de diferentes níveis do curso, não ofereceu diferenças de atuação dos professores nem dos estudantes. Com relação à presença de processos de Matematização, não se pode falar que não existam, uma vez que tanto estudantes quanto professores vão em busca da compreensão dos conteúdos da Física. Porem, não se evidencia desenvolvimento profundo das características da Matematização oferecidas pelos pesquisadores neste tópico
Palabras clave:Ensino de Física. Matematização. Relação matemática e ensino da física. Licenciatura em Física.
Abstract
We present a study about how the Mathematics is understood and worked on a teaching and learning medium, in a course of education for physics teachers, from a public University in Sao Paulo, Brazil. To this objective, we studied different proposals in this research field. We found that the term Mathematization has been introduced in order to represent processes by which learning of physics gain significance when considering formation of skills, such as: observation, description, idealization, local logical analysis, axiomatization and, application. We followed for a year, different subjects of physics in several semesters by filling a daybook. There we registered basic information, contents and development of the classes. Based on the daybook’ analyses, we elaborated an observation guideline with indicators to detect the presence and the way that teachers and students developed processes of Mathematization. With the final guideline, we observed during a semester, a group of several other disciplines. We did a content analysis on the material produced. We note that the fact of observing subjects from different levels of course, didn’t present differences in the performance of teachers neither students. Looking for the presence of Mathematization processes, we cannot talk that doesn’t exist, since both students and teachers go in search of comprehension of physics contents. However, there is no evidence of deep development of Mathematization features offered by the researchers in this topic.
Keywords:Physics teaching. Mathematization. Relation between Maths and Physics teaching. Education for physics teachers.
Introducción
Em nossa busca de resultados de pesquisa sobre o uso da Matemática no Ensino de Física, encontramos que, vem-se introduzindo na literatura o termo de “Matematização”, ao se referir à relação entre a Matemática e o Ensino de Física. Encontramos ainda que existem diversas formas de caracterizar tal Matematização. Por exemplo, segundo Uhden (2012), esta serve como ferramenta (perspectiva pragmática), atua como linguagem (função comunicativa), e prove uma via de razoamento lógico dedutivo (função estrutural). Já segundo Pietrocola (2002) a importância da Matematização está no papel estruturante que ela pode desempenhar no desenvolvimento de processos para a interpretação do mundo físico. Assim, as definições de Matematização contradizem o imaginário que existe entre professores e estudantes de física, no qual para ter sucesso no aprendizado da física é necessário ter um bom domínio da Matemática envolvida, como foi apresentado por (Hudson and McIntire 1977 aput Uhden 2012).
Este estudo objetiva identificar os usos da Matemática nas praticas educativas de Ensino de Física em um grupo de disciplinas do curso de Licenciatura em Física, a fim de analisar as possibilidades de desenvolver processos de Matematização que levem a potencializar a formação de futuros professores de Física, ao formar eles para ir alem da visão pragmática de Matemática como um mero conjunto de algoritmos.
Aportes teórico-conceituais
O objetivo deste capítulo é introduzir uma fundamentação teórica que nos permita entender os significados da “Matematização” da Física ao longo da história. Para tanto, apresentamos algumas evidências de que ao longo da história da Física surgiram diversas formas de entender a relação entre Física e Matemática, em virtude das necessidades e possibilidades predominantes em diferentes épocas e contextos.
Historiadores e filósofos da ciência como Paty (2003), Gingras (2001) e Cantor (1977) desenvolveram estudos sobre o processo de “Matematização” da física, comparando três grandes épocas ao longo de sua história: a primeira trata da filosofia natural desenvolvida na Grécia Antiga; a segunda dá-se na “revolução científica” a partir do século XV e; a terceira, no começo do século XX, com o surgimento da Física Moderna e seus rápidos desenvolvimentos nestes últimos cem anos. Segundo Gingras (2001), o termo “Matematização” aparece com maior frequência nas comparações entre as metodologias e princípios que orientam ou definem o trabalho desenvolvido pelos físicos, principalmente a partir do surgimento da mecânica clássica com os trabalhos de Galileu e Newton.
Tendo ciência de que a evolução da Física não se dá de forma discreta nem linear, mas a partir de continuas tensões, controvérsias, avanços e retrocessos, concebemos esses três periodos como representativos de diferentes perspectivas da relação entre Matemática e Física no desenvolvimento da Física.
Na concepções sobre a “Matematização”, aparecem três aspectos inter-relacionados nos estudos sobre a evolução da Física; o primeiro se refere às considerações sobre o que é “Explicar” um fenômeno físico, que por sua vez depende da “Linguagem” apropriada para apresentar tais explicações e que finalmente se relaciona com o que se considera “Matematizar” um fenômeno físico. Em termos gerais, a “Matematização da Física” é definida como o processo mediante o qual, as metodologias de trabalho dos físicos foram se inter-relacionando cada vez mais com os símbolos, conceitos e metodologias de trabalho da Matemática, para constituir explicações mais completas a cada vez.
Surge em nós, a questão sobre as implicações da compreensão ao pensarmos o Ensino da Física. Partimos do pressuposto de que posicionar-se como professor de Física implica de uma parte compreender o modo como as relações entre Física e Matemática têm sido desenvolvidas na construção do conhecimento científico; e de outra parte, compreender os processos de ensino e aprendizagem em sala de aula. A ligação entre estes dois aspectos, constitui-se em objeto de pesquisa, uma vez que, embora a Física e o Ensino da Física compartilhem o mesmo saber disciplinar sobre o estudo da natureza, são campos diferentes em sua epistemologia, fins, formas de evolução e suportes teóricos.
Assim, entendemos que compreender a forma como a linguagem da Física foi se matematizando durante sua evolução, permite-nos aprofundar no conhecimento de seus conteúdos e, consequentemente, pode garantir um maior preparo do professor. Contudo, ao levar este conhecimento para sala de aula, o professor deve tomar certas decisões para orientar o aprendizado por meio dos processos de Matematização.
Portanto podemos dizer que a pesquisa em Física propõe-se a explicar a natureza, embasando suas explicações na formulação de leis que dêem conta do comportamento dos fenômenos físicos, para os quais têm se utilizado linguagens (formas de descrever e comunicar) apropriadas em diferentes épocas, de acordo com as necessidades de explicação e os conhecimentos prévios sobre um determinado problema. Já no contexto do Ensino de Física, consideramos que os sentidos de termos como “explicar”, “linguagem” e “matematização” apresentam algumas diferenças, uma vez que o profissional deste campo, que é o professor, não se dedica a buscar novas formas de explicar a natureza, mas a explicar para outras pessoas como se explica a natureza. Portanto, a linguagem, entendida no sentido de descrever e comunicar, deve transitar entre as linguagens da Física (para explicar determinados fenômenos) e as linguagens dos alunos (que precisam compreender aspectos da natureza), processo este que não se limita a apresentação da “Matematização” da Física ao longo da história, mas que objetiva orientar os alunos a desenvolverem suas próprias Matematizações.
Metodologia de pesquisa
Nosso campo de observação foi um curso de Licenciatura em Física de uma universidade pública do interior de São Paulo, Brasil. Dentro dele foram escolhidas disciplinas que correspondem a semestres iniciais, intermédios e finais do curso, com o objetivo de obter informações de estudantes “novos” num curso de física, que de alguma maneira não tem sido influenciados pelas dinâmicas de trabalho universitário, estudantes do nível médio dentro do curso, que já tiveram contato com as formas de trabalhar os usos da Matemática para o Ensino de Física na universidade, e estudantes do final de curso que se tem formado para o ensino.
As disciplinas observadas foram; Física II (35 alunos), Física Matemática I (12 alunos), Física Moderna I (24 alunos), sendo elas do segundo, quinto, e sexto semestre respectivamente. Fizemos uma observação não participante durante um ano, na perspectiva de Martins (2008) quando diz que “o observador poderá, ou não, ser um participante da estrutura social que investiga”. Assim, preenchemos um diário de campo registrando aspectos como; dados básicos da disciplina, conteúdos trabalhados, desenvolvimento da aula, e observações gerais. Embasamo-nos na proposta de Estrela (1994) acerca dos aspectos a serem observados em sala de aula, de forma direta e distanciada, considerando todos os elementos constitutivos da aula (professor, alunos, materiais), com o único fim de determinar os “observáveis” a sistematizar na relação Matemática e Ensino de Física.
Como resultado da análise deste diário de campo elaboramos um roteiro de observação que desse conta das características dos processos da Matematização. O roteiro foi constituído com indicadores de existência, uma coluna para marcar com “x” a presença dele, e, uma outra coluna na qual foi registrada a descrição do modo como foi evidenciada a presença do indicador. Foram propostos 16 indicadores para analisar os estudantes, buscando responder perguntas de pesquisa como: 1. Quais significados de Matematização costumam estar presentes na atuação de alunos em sala de aula, em disciplinas de Física do Curso de Licenciatura em Física?; 2. Quais significados de Matematização costumam estar presentes nas explicações sobre assuntos de física, dos alunos do Curso de Licenciatura em Física?.
Também, o roteiro tem 22 indicadores para analisar os professores, buscando responder perguntas como: 3. Como a Matematização costuma estar presente na organização das atividades didáticas de professores do Curso de Licenciatura em Física?; 4. Quais aspectos caracterizam a presença da Matematização nas explicações sobre assuntos de física, em discursos de professores de um curso de Licenciatura em Física?. A coluna numero três, na qual foram registradas as informações do modo como foram evidenciados os indicadores não foi apresentada neste artigo por questões de extensão do documento. Com este roteiro observamos durante um semestre as disciplinas: Física I (45 alunos); Física III (28 alunos), e Laboratório de Física Moderna (Grupo 1, 12 alunos), disciplinas de primeiro, terceiro e sétimo semestre respectivamente.
Acrescentamos que não foi possível fazer a observação nas mesmas disciplinas do ano anterior, por causa do rodízio de disciplinas que se da cada ano neste curso de Licenciatura em Física, mas em geral se mantiveram os mesmos estudantes.
Os roteiros de observação constituíram o texto que foi analisado de forma sistemática para obter inferências sobre o comportamento dos indicadores. Nesta metodologia de análise embasamo-nos nos aportes teóricos e técnicas de Analise de Conteúdo propostos por Bardin, L. Especialmente na análise sistemática da informação a fim de inferir conhecimentos, uma vez que segundo a autora a análise de conteúdo é “um conjunto de técnicas de análise das comunicações visando obter por procedimentos, sistemáticos e objetivos de descrição do conteúdo das mensagens, indicadores (quantitativos ou não) que permitam a inferência de conhecimento relativos as condições de produção”. (BARDIN, 2002)
Resultados
- Consideramos importante salientar que este estudo não objetiva julgar se os professores observados atuaram do jeito “certo” ou não, mas sim analisar a forma como aparecem os indicadores que caracterizam a presença de processos de Matematização. A seguir apresentamos então, os resultados que permitiram-nos constituir respostas para nossas perguntas de pesquisa:
Questão 1: Quais significados de Matematização costumam estar presentes na atuação de alunos em sala de aula, em disciplinas de Física do Curso de Licenciatura em Física?
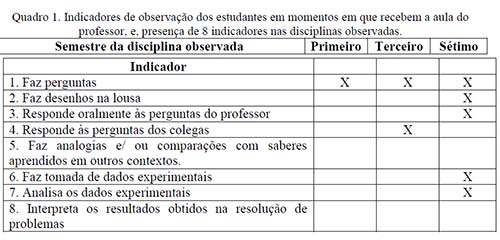
O primeiro indicador ofereceu maior frequência, se apresentando nas aulas observadas do primeiro, terceiro e sétimo semestre. Nessas aulas ao menos um estudante fez perguntas ao professor. Ao analisar o tipo de perguntas, encontramos que a maioria delas pretendia esclarecer o procedimento pelo qual foi resolvido um exercício, a dedução de uma equação, as unidades utilizadas, e em alguns casos solicitando o esclarecimento de termos científicos. O indicador 4 tem presença numa disciplina, também visando esclarecer procedimentos utilizados na resolução de problemas. Pela natureza da disciplina de sétimo semestre ao se tratar de práticas de laboratório, as perguntas foram principalmente sobre o funcionamento dos equipamentos para obter os resultados de forma adequada, e pela mesma razão aparecem os indicadores 2,3,6 e 7, ao ter que apresentar para o professor os resultados obtidos na prática.
Observamos que para os estudantes é suficiente com obter respostas pontuais, sem gerar outros tipos de interação ou complemento nem para as perguntas, nem para as respostas, como poderiam ser por exemplo, o uso de analogias ou comparações com saberes obtidos em outros contextos. Observamos também que tanto na disciplina de tipo experimental quanto nas Teóricas, as perguntas não se constituem em parte de um processo de compreensão de um fenômeno, mas na solução de dificuldades pontuais para desenvolver as atividades indicadas pelos professores, uma vez que não tem presença os indicadores 5 e 8. Concluímos então, que a ideia de Matematização dos estudantes esta relacionada com o bom domínio dos algoritmos envolvidos na resolução de problemas da física.
Questão 2: Quais significados de Matematização costumam estar presentes nas explicações sobre assuntos de física, dos alunos do Curso de Licenciatura em Física?
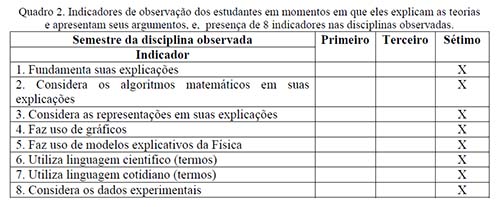
Para evidenciar este grupo de indicadores foi necessário que o estudante falasse em público, razão pela qual não foi possível detectar evidencias nas disciplinas do primeiro e terceiro semestres, uma vez que a metodologia destas disciplinas se desenvolveu principalmente sob a explicação do professor e o trabalho individual e grupal dos estudantes, sem espaço para o aluno apresentar explicações em público. No entanto, a metodologia da disciplina do sétimo termo permitiu-nos observar os estudantes apresentando suas explicações dos resultados obtidos nas práticas de laboratório. Embora todos os indicadores tenham tido presença, a forma como se deu (registrada na coluna do quadro que não esta inserida neste trabalho) permitiu-nos observar algumas particularidades.
Com relação aos indicadores 1 e 2, observamos que as explicações oferecidas pelos estudantes se fundamentam principalmente no uso das equações que descrevem as leis físicas, por exemplo, para explicar a obtenção da velocidade da luz, os alunos descrevem o arranjo experimental com cada uma das partes, falam da tomada do dado sobre a distancia dos espelhos no ponto de interferência das sinais, e logo depois apresentam a equação para inserir os dados e desenvolver o procedimento algorítmico, sem chegar a explicar o principio físico em si mesmo.
No indicadores 3 e 4, observamos o uso de representações como desenhos, fotografias e esquemas de montagens experimentais para fornecer uma determinada visualização do fenômeno a fim de facilitar suas explicações, por exemplo, para explicar a relação inversa entre frequência e comprimento de onda usaram o gráfico de uma onda sinusoidal, também, para explicar o experimento de Millikan usaram um gráfico para apresentar a relação entre energia e carga do elétron. Em geral, estes recursos são utilizados principalmente para dinamizar seu discurso ou para complementar a expressão oral, mas não foram observadas análises o questionamentos sobre os desenhos, fotografias o gráficos utilizados.
Nos indicadores 6 e 7, observamos que usam os termos científicos para garantir exatidão na descrição do fenômeno, e só usam a linguagem cotidiana para fazer comentários adicionais à explicação visando expor os problemas ou acertos que tiveram no desenvolvimento da prática. No indicador 8 observamos que os dados experimentais são usados para compará-los com a teoria, a fim de analisar o grau de exatidão da sua tomada de dados.
Observamos então, que a idéia de Matematização nas explicações dos alunos trata-se de “expor da melhor maneira possível as teorias em estudo”, se fundamentando principalmente na descrição das equações, dos símbolos e representações padrão das teorias, mas sem manifestar dúvidas ou análises, mais alem daquelas relacionadas com a reflexão sobre possíveis causas do erro na tomada de dados experimentais.
Questão 3. Como a Matematização costuma estar presente na organização das atividades didáticas de professores do Curso de Licenciatura em Física?
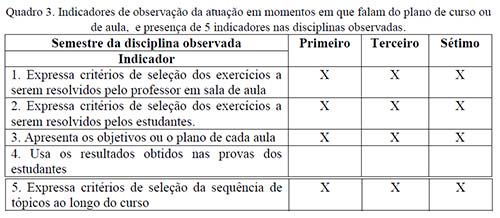
Observa-se que os três primeiros indicadores tem presença em todas as disciplinas. Nos indicadores 1 e 2, os professores manifestam em geral os mesmos critérios de seleção tanto para os exercícios a serem resolvidos por eles em sala de aula, quanto para os exercícios a serem resolvidos pelos estudantes, bem em sala de aula ou como trabalho extraclasse, sendo eles; contribuir na compreensão do tema em estudo, e permitir que os estudantes pratiquem os procedimentos utilizados na solução dos problemas que envolvem os conceitos dos diferentes fenômenos físicos. Para o caso da disciplina de laboratório, a seleção dos experimentos tem a ver com o aprofundamento da temática em estudo e as possibilidades técnicas e logísticas do laboratório.
No indicador 3, os objetivos das diferentes aulas foram apresentados em alguns casos para a aula próxima, em outros casos para um grupo de aulas e em outros casos para o semestre completo como foi o caso da disciplina de laboratório. Nesta disciplina em particular, os estudantes devem preencher um teste no começo de cada aula, a fim de demonstrar seus conhecimentos prévios da prática a ser realizada. A ausência do indicador 4, evidencia que o uso dos resultados das provas aplicadas aos estudantes, sejam escritas ou orais, é para avaliar o conhecimento do estudante até um determinado momento e fornecer as respectivas notas, mas em nenhum dos casos se evidenciou que formasse parte do planejamento das aulas próximas. Com relação ao indicador 5, encontramos que os critérios estão relacionados com condições de pré requisitos para a compreensão de um tema, p. ex, falar de campo elétrico antes de falar de campo eletromagnético. Também encontramos os critérios da contextualização histórica de uma problemática da Física para compreender como ela foi resolvida, ou o seguimento da sequência sobre como foi desenvolvida a física ao longo da historia, na tentativa de ir do simples ao complexo.
Concluímos então, que a idéia de Matematização se relaciona com a compreensão dos fenômenos físicos, no sentido de lhes permitir aos alunos aplicar a teoria na resolução de problemas, compreender as variáveis envolvidas e descrever os fenômenos em estudo. A organização da sequência de atividades, visa principalmente ir gradativamente acrescentando a complexidade dos problemas a serem resolvidos e o aprofundamento das teorias em estudo. Sendo estes processos orientados pelos procedimentos da Física em si mesma.
Questão 4. Quais aspectos caracterizam a presença da Matematização nas explicações sobre assuntos de física, em discursos de professores de um curso de Licenciatura em Física?
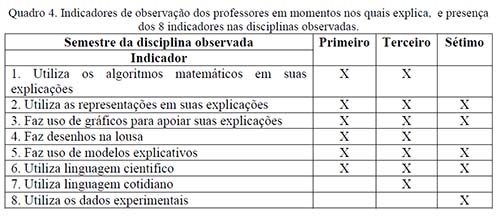
Com relação ao indicador 1 da questão 4, observamos o uso dos algoritmos matemáticos em exercícios de dedução matemática das equações que descrevem as diferentes leis da Física, ou na análise do comportamento das variáveis sob determinadas condições. Nos indicadores 2 e 3 observamos que quando o professor encara a necessidade de representar o fenômeno físico usa representações e gráficos como complemento a sua exposição oral, especialmente para ilustrar as equações ou os resultados de dados experimentais. O indicador 4 deixa ver que o professor usa desenhos para esclarecer idéias que possam aparecer confusas, por exemplo, o desenho de um anel para falar da sua carga e seu potencial elétrico. No indicador 5 encontramos o uso de modelos explicativos das teorias cientificas, por exemplo, a descrição do modelo de campo elétrico explicando a direção da Força em relação às direções do campo e da corrente elétrica, se apoiando na representação do campo com setas e no gráfico de curvas equipotenciais.
No indicador 6 observamos que a maior parte do tempo os professores utilizam linguagem cientifica, quer dizer, uso de termos cujas definições são exatas, em procura de maior clareza e exatidão na descrição dos fenômenos físicos. Já a linguagem do cotidiano aparece nas explicações de fatos do dia a dia, por exemplo, falar de “baterias” de carro, para comparar com capacitores no tema de eletricidade, evidenciando o indicador 7. O indicador 8 não aparece nas disciplinas teóricas, uma vez que a prática experimental não faz parte das atividades de ensino.
Conclusões
Em primeiro lugar constatamos que o fato de observar disciplinas de diferentes níveis no curso, não ofereceu diferenças de atuação dos professores nem dos estudantes.
Com relação à presença de processos de Matematização, não se pode falar que não existam, uma vez que tanto estudantes quanto professores vão em busca da compreensão dos conteúdos da Física. Porem, não se evidencia desenvolvimento profundo das características da Matematização oferecidas pelos pesquisadores neste tópico, em aspectos como:
- O estudo dos fenômenos se desenvolve principalmente por meio do uso de problemas, formulações, símbolos e axiomas, a partir de um modelo explicativo definido, fato que poderia ser enriquecido ao orientar o estudante para a observação e busca das características essenciais em cada um desses aspectos.
- A principal via de aplicação dos conteúdos estudados é a partir do uso dos algoritmos, fato que pode ser potencializado ao trabalhar em processos de formação de habilidades para esquematizar, algoritmizar, simbolizar e formalizar a descrição dos fenômenos físicos, se servindo de recursos de análise, como por exemplo, as analogias.
- O uso da Historia da Física é principalmente para colocar problemas cruciais no desenvolvimento das teorias, abordagem que pode ser ampliada ao envolver os estudantes em situações paradigmáticas.
- Os professores procuram a maior exatidão possível nas explicações por meio do uso dos termos científicos, e os estudantes assumem que explicar é usar corretamente os termos científicos utilizados pelo professor. Embora esta situação contribua para o aprendizado, poderia ser enriquecida ao procurar cada vez uma compreensão mais aprofundada dos termos científicos utilizados, por meio de processos de produção de esquemas, e estratégias de organização da informação, ou de situações problema que levem ao estudante a construir argumentos permitindo-lhes tomar posição critica perante a linguagem utilizada.
Insistimos em que nosso interesse não é julgar o agir dos professores, mas determinar o estado de seus pressupostos com relação a “Matematização” no ensino de Física. Vemos como ainda com as particularidades que necessariamente tem cada professor em função de suas personalidades, de seus conhecimentos, da disciplina que ministra, entre outros aspectos, é possível detectar algumas tendências que ao ser analisadas, oferecem um panorama a partir do qual podem ser organizadas discussões acadêmicas respeito das formas de ligar a teoria produzida pela pesquisa em ensino de Física com a prática do ensino de Física na formação inicial de professores.
Referências
BARDIN, L. Análise de Conteúdo. Edições 70. Lisboa, 2002.
CANTOR, G. N. Berkeley, reid, and the mathematization of mid-eighteenth-century optics. Journal of the History of Ideas, Pennsylvania, v.38, n.3, pp. 429-448, 1977.
ESTRELA, A. Teoria e Prática de Observação de Classes. Editora Porto. Portugal. 4 ed. 1994.
GINGRAS. Y. What did mathematics do to physics? hist. sci., xxxix, 2001.
MARTINS, G. Estudo de Caso, Uma estratégia de Pesquisa. Editora Atlas. São Paulo. 2008.
PATY. M. The idea of quantity at the origin of the legitimacy of mathematization in physics. Constructivism and practice: towards a social and historical epistemology, Rowman & littlefield, Lanham (md.,USA), p. 109-135, 2003.
PIETROCOLA, M. A Matemática como estruturante do conhecimento Físico. Cad.Cat.Ens.Fís. v.19, n.1: p. 88-108, ago. 2002.
UHDEN, O; KARAM, R; PIETROCOLA, M; POSPIECH, G. Modelling Mathematical Reasoning in Physics Education. Science & Education. Volume 21, Number 4. 2012.
License
Gondola, Ens Aprend Cienc. is an open-access publication, free of charge for authors and readers. The publication, consultation or download of the contents of the magazine does not generate any cost for the authors or the readers, since the Francisco José de Caldas District University assumes the expenses related to edition, management and publication. The peer evaluators do not receive any economic retribution for their valuable contribution. The work of all the actors mentioned above is understood as a contribution to the strengthening and growth of the research community in the field of Science Education.
As of December 1, 2018 the contents of the journal are published under the terms of the Creative Commons License Attribution-Noncommercial- ShareAlike 4.0 International (CC-BY-NC-SA 4.0), under which others may distribute, remix, retouch, and create from the work in a non-commercial way, give credit and license their new creations under the same conditions.
The copyright holders are the authors and the journal Gondola, Ens Aprend Cienc. The holders retain all rights without restrictions, respecting the terms of the license in terms of consultation, downloading and distribution of the material.
When the work or any of its elements is in the public domain according to the applicable law in force, this situation will not be affected by the license.
Likewise, we encourage authors to deposit their contributions in other institutional and thematic repositories, with the certainty that culture and knowledge is a good of all and for all.









.jpg)




















