DOI:
https://doi.org/10.14483/23464712.14350Published:
2020-05-01Un panorama de la modelación matemática en los encuentros colombianos de matemática educativa entre 2012-2015
An overview of mathematical modeling in the Colombian educational mathematics meetings between 2012-2015
Um panorama da modelagem matemática em encontros colombianos de matemática educativa entre 2012-2015
Keywords:
documentary review, mathematical modeling;, Colombian Meeting of Mathematics Education (en).Keywords:
revisión documental, modelación matemática, Encuentro Colombiano de Matemática Educativa (es).Keywords:
revisão documental, modelagem matemática, Encontro Colombiano de Educação Matemática (pt).Downloads
References
ÁLVAREZ, D.; COLORADO, H.; OSPINA, P. Una propuesta didáctica para la enseñanza del concepto de derivada. Revista Científica, Bogotá, v. 1, n. esp., pp. 95-101. 2013. https://doi.org/10.14483/23448350.5961
APONTE, H.; FERNÁNDEZ, J.; VEGA, M. (2015). Modelación matemática a través de fenómenos físicos. La proporcionalidad directa y el principio de Bernoulli. RECME, Bogotá, v. 1, n. 1, pp. 348-352. 2015.
APONTE, P.; ALMÉCIGA, H.; TORRES, D. Apuntes para la enseñanza de objetos matemáticos inmersos en el álgebra escolar. Un paso por diversas investigaciones. Revista Científica, Bogotá, v. 1, n. esp., pp. 345-350. 2013. https://doi.org/10.14483/23448350.7071
ARAÚJO, J. Uma Abordagem Sócio-Crítica da Modelagem Matemática: a perspectiva da educação matemática crítica. ALEXANDRIA Revista de Educação em Ciência e Tecnologia, Florianópolis, Brasil, v. 2, n. 2, pp. 55-68, 2009.
ARENDT, H. La condición humana. 1993. Disponible en: http://www.perio.unlp.edu.ar/catedras/sites/default/files/arendt_h_-_la_condicion_humana_prologo_byn.pdf.
BARBOSA, J. Mathematical modelling in classroom: A socio-critical and discursive perspective. ZDM, Alemania, v. 38, n. 3, pp. 293-301, 2006. https://doi.org/10.1007/BF02652812
BOLAÑOS, J; ARBOLEDA, C.; MOTATO, J. (2016). Sistematización de una experiencia para la enseñanza del movimiento parabólico y su relación con el modelo termodinámico: una vía para fortalecer el pensamiento científico en los estudiantes de Licenciatura en matemáticas y física de Universidad del Valle. Revista Colombiana de Matemática Educativa, Bogotá, v. 1, n. 1b, p. 150. 2016.
BOSSIO, J.; LONDOÑO, S.; JARAMILLO, C. Modelación matemática en el aula clase: una producción de modelos lineales desde el contexto del cultivo de plátano. Revista Científica, Bogotá, v. 1, n. esp., pp. 409-412. 2013. https://doi.org/10.14483/23448350.6507
BOTELLO, I.; PARADA, S. La evaluación del Pensamiento Variacional de los estudiantes de recién ingreso a la Universidad. Revista Colombiana de Matemática Educativa, Bogotá, v. 1, n. 1b, p. 146. 2016.
BUSTOS, A.; BUSTOS, G.; NOVOA, Y. Propuesta de ambientes de aprendizaje para la promoción de la modelación matemática desde la perspectiva crítica. Revista Científica, Bogotá, v. 1, n. esp., pp. 95-101. 2013.
CETINA, M.; CABAÑAS, G.; VILLA, J. Situaciones realistas y la matematización de la función cuadrática. Revista Colombiana de Matemática Educativa, Bogotá, v. 1, n. 1b, pp. 151-152. 2016.
CHÁVEZ, A.; SAMBONI, T. No le des la espalda a tu espalda. Cuidado del cuerpo y matemáticas. RECME, Bogotá, v. 1, n. 1, pp. 369-374. 2015.
COLOMBIA. Ministerio de Educación Nacional. Lineamientos curriculares. Área Matemáticas. Cooperativa Editorial del Magisterio, Bogotá: Colombia. 1998.
CUMBAL, L. La modelación matemática como proceso de estudio en el álgebra escolar. En: 13 ENCUENTRO COLOMBIANO DE MATEMÁTICA EDUCATIVA. Medellín: Colombia. 2012.
DUARTE, P.; RENDÓN, P.; VILLA, J. La modelación matemática: una experiencia de formación en ingeniería. RECME, v. 1, n. 1, pp. 440-445. 2015.
ECHEVERRY, F.; AUDOR, Y. La matemática en los malabares. Revista Científica, Bogotá, v. 1, n. esp., pp. 303-307. 2013. https://doi.org/10.14483/23448350.7059
ESPINOSA, J. Solución de modelos matemáticos, utilizando el software Derive 6.1 en aplicaciones de ecuaciones diferenciales de primer orden. En: 13 ENCUENTRO COLOMBIANO DE MATEMÁTICA EDUCATIVA. Medellín: Colombia. 2012
ESPINOSA, J.; HERNÁNDEZ, H.; YÁÑEZ, L. Descripción de la producción de etanol a partir de desechos orgánicos domésticos y hojarasca, utilizando modelos matemáticos aplicados en el software Derive 6.1 y la hoja de cálculo Excel. Revista Científica, Bogotá, v. 1, n. esp., pp. 700-704. 2013. https://doi.org/10.14483/23448350.7755
GALÁN, G.; RODRÍGUEZ, Y. Dibujando la realidad usando las Isometrías en el plano bidimensional. Revista Científica, Bogotá, v. 1, n. esp., pp. 709-711. 2013. https://doi.org/10.14483/23448350.7757
GALLEGO, L.; ALDANA, E. Análisis de la concepción de la actividad de optimizar, desde una ingeniería didáctica. Revista Científica, Bogotá, v. 1, n. esp., pp. 216-219. 2013. https://doi.org/10.14483/23448350.6486
GÓMEZ, O. Desarrollo del pensamiento variacional en estudiantes de grado noveno. Revista Científica, Bogotá, v. 1, n. esp., pp. 115-120. 2013. https://doi.org/10.14483/23448350.5966
GÓMEZ, P. et al. Aspectos sociocríticos en la modelación matemática: una revisión documental. RECME, Bogotá, v. 1, n. 1, pp. 353-358. 2015.
GONZÁLEZ, S.; MUÑOZ, L.; LÓPEZ, C. Reflexiones docentes a partir de actividades de modelación matemática. RECME, Bogotá, v. 1, n. 1, pp. 399-403. 2015.
GUERRERO, F.; SALAS, J. Narrativas de los derechos humanos en educación matemática: el caso de los estudiantes de grado sexto. RECME, Bogotá, v. 1, n. 1, pp. 451-455. 2015.
HENAO; VANEGAS. La modelación matemática en la educación matemática realista: un ejemplo a través de la producción y uso de modelos cuadráticos. En: 13 ENCUENTRO COLOMBIANO DE MATEMÁTICA EDUCATIVA. Medellín: Colombia. 2012.
HERNÁNDEZ, E.; CUEVAS, J. Razonamiento estadístico en estudiantes de quinto de primaria a partir de predicciones en torno a la idea de resistencia física. Revista Científica, Bogotá, v. 1, n. esp., pp. 551-554. 2013. https://doi.org/10.14483/23448350.7723
KAISER, G.; SRIRAMAN, B. A global survey of international perspectives on modelling in mathematics education. ZDM, v. 38, n. 3, pp. 302-310. 2006. https://doi.org/10.1007/BF02652813
MARCILLO, A.; ROJAS, C.; VILLA, J. Procesos de comunicación en la modelación matemática escolar. RECME, Bogotá, v. 1, n. 1, pp. 392-398. 2015.
MARTÍNEZ, D., PÁEZ, O.; GARCÍA, G. Modelación desde la perspectiva de la educación matemática crítica. Cuestiones relacionadas con la obsolescencia. Revista Científica, Bogotá, v. 1, n. esp., pp. 288-292. 2013. https://doi.org/10.14483/23448350.7054
MOLINA, J.; VILLA, J. La modelación en la producción de conocimiento matemático: el caso de la función seno. Revista Científica, Bogotá, v. 1, n. esp., pp. 80-84, 2013. https://doi.org/10.14483/23448350.5496
MOLLOGÓN, J. Un problema de alturas en el Guaviare. Revista Científica, Bogotá, v. 1, n. esp., pp. 523-527. 2013.
MORENO, J. La modelación matemática en el contexto de la robótica: una actividad didáctica realizada por aprendizaje de proyectos para el concepto de proporción. En: 13 ENCUENTRO COLOMBIANO DE MATEMÁTICA EDUCATIVA. Medellín: Colombia. 2012.
OBANDO, J.; SÁNCHEZ, J.; MUÑOZ, L.; VILLA, J. El reconocimiento de variables en el contexto cafetero y su constitución como modelos matemáticos. En: 13 ENCUENTRO COLOMBIANO DE MATEMÁTICA EDUCATIVA. Medellín: Colombia. 2012.
OLMOS, C.; SARMIENTO, D.; MONTEALEGRE E. Competencia matemática modelizar: un estudio exploratorio desde la función cuadrática. En: 13 ENCUENTRO COLOMBIANO DE MATEMÁTICA EDUCATIVA. Medellín: Colombia. 2012.
PARRA, M.M.; VILLA, J. Tendencias en investigación en modelación matemática en educación primaria. RECME, Bogotá, v. 1, n. 1, pp. 235-240. 2015.
PEDREROS, M.; MEJÍA, M. Relaciones e integraciones de la Teoría Antropológica de lo Didáctico y la Génesis Instrumental. Revista Científica, Bogotá, v. 1, n. esp., pp. 397-401. 2013.
PERDOMO, E.; TAFUR, Y.; MARTÍNEZ, J. La conversión entre los registros de representación de la función lineal y criterios de congruencia entre algunas de sus representaciones. RECME, Bogotá, v. 1, n. 1, pp. 72-77. 2015.
PERILA, W.; MANCERA, G.; CAMELO, F. La telefonía móvil en Colombia: un ambiente de modelación matemática desde una perspectiva crítica. RECME, Bogotá, v. 1, n. 1b, pp. 100-101. 2016.
PLANAS, N.; VALERO, V. Tracing the socio-cultural-political axis in understanding mathematics education. En BOERO, P.; LEDER, G. (eds.). The Second Handbook of the Psychology of Mathematics Education. The journey continues. Sense Publishers. Róterdam: Países Bajos. 2016. pp. 447-449. https://doi.org/10.1007/978-94-6300-561-6_13
PUERTO J. El uso de los fractales para potenciar el desarrollo del pensamiento algebraico-variacional a través del software Cabrí "Del pensamiento numérico al pensamiento Algebraico-Variacional". Revista Científica, Bogotá, v. 1, n. esp., pp. 665-669. 2013. https://doi.org/10.14483/23448350.7747
RENDÓN, P.; ESTEBAN, P; VILLA. J. La modelación matemática en la ingeniería de diseño. Revista Científica, Bogotá, v. 1, n. esp., pp. 102-106. 2013. https://doi.org/10.14483/23448350.5962
RIVERA, S.; LONDOÑO, S.; JARAMILLO, O. Medida de área y el volumen en contextos auténticos: una alternativa de aprendizaje a través de la modelación matemática. En: 13 ENCUENTRO COLOMBIANO DE MATEMÁTICA EDUCATIVA. Medellín: Colombia. 2012
ROMERO, J.; BARRIOS, O.; GALVIS, T. Emergencia de discusiones en un proceso de modelación matemática desde la perspectiva socio-crítica. Revista Colombiana de Matemática Educativa, Bogotá, v. 1, n. 1b, p. 156. 2016.
SÁNCHEZ, J. et al. Posibilidades y limitaciones de la Modelación Matemática a través de proyectos. Una experiencia en formación inicial de profesores. RECME, Bogotá, v. 1, n. 1b, pp. 130-131. 2016.
SÁNCHEZ, J.; OBANDO, J.; MUÑOZ, L.; VILLA, J. La modelación matemática: Un ejemplo en el contexto cafetero. Revista Científica, Bogotá, v. 1, n. esp., pp. 474-478. 2013. https://doi.org/10.14483/23448350.6570
SIERRA, L.; MONRROY, N. Análisis de la metástasis en el sistema linfático, con grafos y cadenas de Markov. Revista Colombiana de Matemática Educativa, Bogotá, v. 1, n. 1b, p. 86. 2016.
TAVERA, F.; VILLA, J. El pensamiento variacional en el estudio de las relaciones trigonométricas: una mirada desde los libros de texto. Revista Científica, Bogotá, v. 1, n. esp., pp. 298-302. 2013. https://doi.org/10.14483/23448350.7058
VALERO, P. Consideraciones sobre el contexto y la educación matemática para la democracia. Quadrante, Portugal, v. 11, n. 1, p. 33-40, 2002.
How to Cite
APA
ACM
ACS
ABNT
Chicago
Harvard
IEEE
MLA
Turabian
Vancouver
Download Citation
UN PANORAMA DE LA MODELACIÓN MATEMÁTICA EN LOS ENCUENTROS COLOMBIANOS DE MATEMÁTICA EDUCATIVA ENTRE 2012 Y 2015
AN OVERVIEW OF MATHEMATICAL MODELING IN THE COLOMBIAN EDUCATIONAL MATHEMATICS MEETINGS BETWEEN 2012-2015
UM PANORAMA DA MODELAGEM MATEMÁTICA EM ENCONTROS COLOMBIANOS DE MATEMÁTICA EDUCATIVA ENTRE 2012-2015
Gabriel Mancera Ortiz* y Francisco Javier Camelo Bustos**
En la medida en que realmente pueda llegarse a “superar” el pasado, esa superación consistiría en narrar lo que sucedió.
Hannah Arendt
Cómo citar este artículo: Mancera Ortiz, G. y Camelo Bustos, F. J. (2020). Un panorama de la modelación matemática en los encuentros colombianos de matemática educativa entre 2012 y 2015. Gdola, ensenza y aprendizaje de las ciencias, 15(2), 251-267. DOI: http://doi.org/10.14483/23464712.14350
Recibido: 21 de enero de 2019; aprobado: 02 de junio de 2019
* Doctor en Educación. Profesor de la Universidad Distrital Francisco José de Caldas, Bogotá (Colombia). Correo electrónico: gmancerao@ udistrital.edu.co –
** Doctor en Educación. Profesor de la Universidad Distrital Francisco José de Caldas, Bogotá (Colombia). Correo electrónico: fjcamelob@ udistrital.edu.co
Resumen
Presentamos el análisis, los resultados y el método de una revisión de tipo documental que da cuenta de aspectos, que consideramos importantes, sobre el reconocimiento que diversos trabajos han venido haciendo sobre la modelación matemática en Encuentros Colombianos de Matemática Educativa (ECME) celebrados entre 2012 y 2015. Para ello, hemos adaptado las tres etapas propuestas por Planas, Valero (2016) para el análisis de estados del arte: selección (de literatura), estructuración (búsqueda de perspectivas, líneas y conexiones) y análisis (novedades), con la intención de identificar posibles perspectivas, líneas de preocupación, conexiones (o desconexiones) entre esas líneas, representantes y regiones de donde proceden los trabajos. Encontramos que los trabajos se clasifican en ocho perspectivas, evidenciando mayor producción en la perspectiva educacional, sociocrítica y realista. En cuanto a las líneas de preocupación señalamos la existencia de un énfasis en el desarrollo de trabajos que plantean a la modelación como medio para la enseñanza o aprendizaje de contenidos; seguido de una preocupación por utilizarla para el desarrollo de algún tipo de pensamiento crítico. De igual manera, se evidenció un mayor interés de producción y difusión en los trabajos que proceden de las ciudades de Bogotá, Medellín y Cali.
Palabras clave: revisión documental; modelación matemática; Encuentro Colombiano de Matemática Educativa.
Abstract
This paper presents the analysis, results, and the method used by a documentary or bibliographic review to give an account of aspects that we consider important in the recognition of the work that has been carried out on mathematical modeling in Colombian Meetings of Educational Mathematics (ECME) held between 2012 and 2015. It has adopted the three stages proposed by Planas and Valero (2016)—selection (of literature); structuring (search for perspectives, lines, and connections); and analysis (novelties)—for the analysis of the state of the art, with the intention of identifying possible perspectives, lines of concern, connections (or disconnections) between those lines, representatives, and regions where the works come from. The findings of this study reveal that the works are classified in eight perspectives, with greater production being evidenced in the educational, socio-critical, and perspectives. As for the lines of concern, the results point to the existence of an emphasis on the development of works that portray modeling as a means of teaching or learning content, followed by a concern to use it for the development of some kind of critical thinking. Similarly, within what is evidenced, the results indicate that there is significant interest in the production and dissemination of the works that come from the cities of Bogota, Medellin, and Cali.
Keywords: documentary review; mathematical modeling; Colombian Meeting of Mathematics Education.
Resumo
Apresentamos a analise, os resultados e o método de uma revisão de tipo documental que da conta de aspectos, que consideramos importantes, referente ao reconhecimento que muitos trabalhos tem feito sobre a modelagem matemática nos Encontros Colombianos de Matemática Educativa (ECME) realizados entre 2012 e 2015. Para isso, adaptamos as três etapas propostas por Planas e Valero (2016) para a análise de estados de arte: Seleção (da literatura), estruturação (busca de perspectivas, linhas e conexões) e análise (novidades), com a intenção de identificar possíveis perspectivas, linhas de preocupação, conexões (ou desconexões) entre essas linhas, representantes e regiões onde são produzidas as pesquisas. Verificamos que os trabalhos são classificados em oito perspectivas, evidenciando maior produção na perspectiva educacional, sócio crítica e realística. Em relação às linhas de preocupação, ressaltamos a existência de uma ênfase no desenvolvimento de trabalhos que propõem a modelagem como meio de ensino ou aprendizagem de conteúdos; seguido de uma preocupação em usá-la para o desenvolvimento de algum tipo de pensamento crítico. Da mesma forma, dentro do que se pode evidenciar, vemos que há um interesse maior na produção e divulgação nos trabalhos que vêm das cidades de Bogotá, Medellín e Cali.
Palavras-chave: revisão documental; modelagem matemática; Encontro Colombiano de Educação Matemática.
1. Abriendo puertas
El introducirnos en la modelación matemática (MM) en la educación matemática, en Colombia, nos permitió reconocer la importancia que tiene este proceso en el desarrollo del pensamiento matemático. En Colombia, el Ministerio de Educación Nacional (MEN) publicó unos lineamientos curriculares, y específicamente en el área de matemáticas se considera a la MM como uno de los cinco procesos generales de la actividad matemática (Colombia, 1998). Sin embargo, dicho reconocimiento, por parte de nosotros, no siempre ha sido así, pues, si bien observábamos (y advertimos) la potencia de la MM en el contexto escolar, éramos (y somos) conscientes de que, a pesar de llevar un lapso de tiempo considerable, planteado como una orientación para el diseño y trabajo en el currículo colombiano1, no se accedía fácilmente a mayores evidencias sobre su desarrollo tanto teórico como práctico en nuestro contexto nacional.
De hecho, para nosotros mismos en un principio, la MM no fue considerada una actividad matemática que vislumbraba una potencia importante en la escuela, pues la percibíamos de difícil realización en el aula de clase si se tiene en cuenta la crono-génesis a la que el currículo colombiano era (y es) fiel, por el carácter hegemónico de las prácticas tradicionales de enseñanza. Era, en su momento, una utopía o una fantasía, por decirlo de otra manera, hecho que se reforzaba si reconocemos que, en un sector de los profesores e investigadores en el país, tenía –y aún tiene– la percepción que, en cuanto a la MM, estamos a la zaga de los avances internacionales en este aspecto.
Lo anterior nos hace recordar el epígrafe de este documento. Tomándolo como excusa, creemos coherente y obligatorio ser conscientes de la evolución de este proceso general de la actividad matemática en Colombia, para no seguir perpetuando el olvido –y su desconocimiento– en el que ha caído. Dicho de otra forma, queremos analizar qué pasó en relación con la MM en la educación matemática en Colombia, para narrarlo y comprender su presente.
Para dar cuenta de lo anterior, presentamos en este documento un estudio preliminar, de carácter bibliométrico, con el ánimo de abrir una ventana que permita empezar a narrar lo que sucedi. Para ello, hemos tomado las memorias de los últimos cuatro Encuentros Colombianos de Matemática Educativa (ECME), por cuanto consideramos es el evento que agrupa, en el ámbito nacional, un gran número de investigadores y profesores en educación matemática. Esperamos que se constituya tan solo en un punto de partida, el cual posibilite abrir espacios para el desarrollo de trabajos de mayor aliento y envergadura.
2. Revisando la literatura: ¿Qué y cómo lo hicimos?
En lo que se refiere a la MM en el contexto colombiano, fuimos convenciéndonos de que era –y es– necesario empezar a revisar su pasado para entender su presente, lo que nos llevó a enfrentarnos a preguntas como: ¿Cómo proceder en esa revisión de la literatura?, ¿qué lógica seguir y adoptar en nuestro empeño?, ¿qué preguntas orientadoras plantearnos?, ¿dónde buscar la información requerida? Una primera aproximación a la reflexión de estas cuestiones nos condujo a aceptar que la tarea debía ser realizada en diferentes etapas y acotando los lugares y tiempos en que debíamos buscar los documentos a analizar. Por lo que surgió un sinnúmero de fuentes y momentos en los cuales desarrollar la búsqueda de los documentos a analizar –algunos con mayor o menor complejidad–, pues podríamos encontrar evidencias en: revistas especializadas, trabajos para optar por el título de pregrado, tesis de maestría y doctorado, memorias de eventos especializados –a regionales, nacionales e internacionales–, etc.
Dado que este trabajo se refiere a un estado del arte (preliminar) de la MM en Colombia, la pregunta a responder era: ¿Cuál de las anteriores fuentes es la más adecuada para realizar un estudio inicial y modesto en torno a la revisión de la literatura en nuestro campo?
Basados en nuestra experiencia y conocimiento de la comunidad académica en la educación matemática colombiana, era posible establecer que las bases de datos para ubicar los trabajos de grado, tesis de maestría y doctorado no serían de fácil acceso, pues en muchas universidades apenas se está instaurando la exigencia de poseer tales bases de datos o repositorios y, en otras, ellas son inexistentes, por lo que no era una opción viable a nuestros ojos iniciar por este camino.
En cuanto a las revistas especializadas existe un sinnúmero de posibilidades en donde los investigadores del campo pueden realizar sus publicaciones. Sin embargo, debemos reconocer que solo existen dos revistas especializadas y reconocidas por la comunidad académica nacional que se concentran en la educación matemática en Colombia. Una de ellas enfocada en estudios de corte sociocultural y etnomatemático, y la otra, apenas cuenta con dos volúmenes y tres números lanzados a la comunidad, por lo que no se constituyen, desde nuestras perspectivas, en una rica fuente para el análisis de corte documental sobre la MM.
Por su parte, las memorias en eventos especializados son, en su mayoría, de corte regional, aspecto que, creemos, limita de alguna manera nuestro empeño de cubrir todo el territorio nacional. Afortunadamente, contamos con un evento en educación matemática que por más de tres lustros ha intentado abarcar trabajos en todo el país. Dicho evento, denominado Encuentro Colombiano de Matemática Educativa (ECME), se ha desarrollado anualmente, tomando su sede en diferentes ciudades a lo largo y ancho del territorio nacional, con el objeto de llegar a la mayor cantidad de profesionales e investigadores. Por lo que decidimos realizar nuestra exploración en sus memorias.
La pregunta que abordamos a continuación fue la de cómo limitar en el tiempo el estudio a realizar, pues el ECME ha desarrollado 16 encuentros desde 1999. Decidimos tomar como punto de partida los últimos cuatro, pues consideramos que, al ser un estudio preliminar, un lapso mayor desbordaría nuestras posibilidades en el volumen de la información.
Nuestro siguiente paso se constituyó en enfrentarnos a la tarea de identificar preguntas orientadoras que nos permitieran localizar, al menos, las siguientes cuestiones: ¿Qué perspectivas son expresadas en los trabajos que localizaremos?, ¿qué líneas de preocupación puede evidenciarse?, ¿existen conexiones –o desconexiones– entre esas líneas?, ¿quienes las representan?, y ¿de qué regiones proceden sus trabajos?
Con el propósito de dar respuesta a estas preguntas, adaptamos las etapas propuestas por Planas, Valero (2016) para la elaboración de estados de arte: selección –de literatura–, estructuración –búsqueda de perspectivas, líneas y conexiones– y análisis –novedades–. Siendo las etapas de carácter inductivo, pues no establecemos de antemano categorías conceptuales a identificar. A continuación, pasaremos a desarrollar tales etapas.
a. Etapa de selección
Consistió en elegir el conjunto de documentos a estudiar. Aquí identificamos, en las memorias de los ECME desarrollados en los años 2012, 2013, 2014 y 2015, los documentos que en cualquier apartado mencionaran las palabras: modelaci, modelaje o modelo. De este ejercicio, se obtuvieron 73 documentos (7 en 2012, 43 en 2013, 10 en 2014 y 13 en 2015). Luego, descartamos aquellos en donde el uso de las palabras anteriores no condujera a una explicitación de la MM –por ejemplo: modelo de Van Hiele–, de lo cual se obtuvieron 41 –7 en 2012, 18 en 2013, 9 en 2014 y 7 en 2015–2.
b. Etapa de estructuración
Aquí identificamos si los documentos son resultado de una investigación, de un proceso de formación o de la reflexión de un colectivo de trabajo; además de qué tipo de población se impacta y si son trabajos teóricos o prácticos. Lo anterior nos condujo a establecer que el tratamiento que el (los) autore(s) da(n) a la MM en ocasiones no se explicita ni se profundiza. Generalmente tal sentido plantea que es un proceso para llegar a una representación que involucra conceptos matemáticos de una situación no matemática tomada de la realidad. Tal intención se presenta a continuación, discriminada evento por evento.
ECME 13 (2012)
En la versión número 13 del ECME identificamos siete documentos: Henao, Vanegas (2012) [13-1]3; Obando, Sánchez, Muñoz, Villa (2012) [13-2]; Olmos, Sarmiento, Montealegre (2012) [13-3]; Moreno (2012) [13-4]; Espinosa (2012) [13-5]; Cumbal (2012) [13-6]; Rivera, Londoño, Jaramillo (2012) [13-7]. En todos ellos se hace explícita una intención de plantear actividades para ser desarrolladas en el aula, por lo que los catalogamos como de corte práctico. No obstante, en uno de ellos se presenta una reflexión teórica de revisión documental, previa a la organización del diseño que los autores desean plantear, por lo que podría considerarse a su vez de corte teórico ([13-1]). Cinco de tales trabajos están dirigidos a desarrollar actividades con estudiantes de secundaria ([13-2], [13-3], [13-4], [13-6] y [13-7]) y dos con estudiantes universitarios ([13-1] y [13-4]), siendo las temáticas trabajadas muy diversas, pues van desde un tratamiento de la función cuadrática, pasando por conceptos de volumen y área, hasta las ecuaciones diferenciales; incluso, uno de los trabajos se centra más en aplicaciones hacia la robótica.
Todos los documentos dan cuenta de procesos investigativos; dos de ellos desarrollados por profesores universitarios ([13-1] y [13-5]), cuatro por estudiantes de maestría ([13-3], [13-4], 13-6] y [137]) y uno por un grupo de profesores e investigadores ([13-2]), siendo las ciudades donde se desarrollan Cali –tres ([13-1], [13-4] y [13-6])–, Medellín –dos ([13-2] y [13-7])–, Florencia –uno ([13-3])– y Bucaramanga –uno ([13-5])–.
ECME 14 (2013)
Durante la versión 14 del ECME observamos que dieciocho documentos hacen algún tipo de alusión a la modelación: Molina, Villa (2013) [14-1]; Álvarez, Colorado, Ospina (2013) [14-2]; Rendón, Esteban, Villa (2013) [14-3]; Gómez (2013) [14-4]; Gallego, Aldana (2013) [14-5]; Bustos, Bustos, Novoa (2013) [14-6]; Martínez, Páez, García (2013) [14-7]; Tavera, Villa (2013) [14-8]; Echeverry, Audor (2013) [14-9]; Aponte, Alméciga, Torres (2013) [14-10]; Pedreros, Mejía (2013) [14-11]; Bossio, Londoño, Jaramillo (2013) [14-12]; Mogollón (2013) [14-13]; Sánchez, Obando, Muñoz, Villa (2013) [14-14]; Hernández, Cuevas (2013) [14-15]; Puerto (2013) [14-16]; Espinosa, Hernández, Yáñez (2013) [14-17], y Galán, Rodríguez (2013) [14-18]. Dos tuvieron un corte de carácter teórico ([14-3] y [14-7]) y diecisiete prácticos ([14-1], [14-2], [14-4], [14-5], [14-6], [147], [14-8], 14-9], [14-10], [14-11], [14-12], [1413], [14-14], [14-15], [14-16], [14-17] y [14-18]). En cuanto a los segundos, puede decirse que dan cuenta de propuestas de enseñanza o aprendizaje (algunos de ellos usando tecnología) ([14-1], [14-2], [14-4], [14-6], [14-10], [14-13], [14-16] y [14-18]) análisis en el proceso de MM realizados por los estudiantes ([14-7], [14-12] y [14-14]), exhibición de las relaciones existentes entre la matemática y otro tipo de actividades de carácter cultural (los malabares ([14-9]), el uso de la modelación como herramienta de formación para ingenieros y trabajos cuyo objetivo no está centrado en la MM, pero la menciona para alcanzar sus objetivos ([14-8], [14-5], [14-8], [14-15] y [14-17]). En cuanto a los documentos de carácter teórico, uno ([14-3]) plantea una discusión acerca de cómo la MM puede convertirse en una herramienta de formación para los ingenieros (propiamente en Ingeniería de Diseño) y el otro ([14-7]) exhibe aspectos relacionados con las dificultades que presenta la modelación, desde la perspectiva sociocrítica, en el sentido de Barbosa (2006) y Araújo (2009), para integrarse al currículo de matemáticas (del grado octavo) y como parte de las prácticas en la clase.
Once documentos plantearon actividades para ser desarrolladas en el aula con estudiantes de básica y media ([14-1], [14-4], [14-6], [14-7], [1410], [14-12], [14-13], [14-14], [14-15], [14-16], [14-18]), tres con estudiantes de pregrado ([14-2], [14-3] y [14-5]), uno a malabaristas profesionales de la ciudad de Cali ([14-9]) y tan solo en tres casos no fue posible reconocer la población a la que fue dirigido ([14-8], ([14-11] y ([14-17]). En nueve casos no fue posible identificar en qué marco fue desarrollada la experiencia ([14-2], [14-6], [14-8], [14-9], [14-11], [14-13], [14-16], [14-17] y [14-18]), mientras que dos fueron elaborados en el ámbito de una investigación ([14-5] y [14-12]), una corresponde a la investigación desarrollada alrededor de un proyecto doctoral ([14-3]), cuatro como trabajo de maestría ([14-1], [14-4], [14-7] y [14-14]), una en un espacio de formación de pregrado ([14-10]) y una en el marco de una práctica docente ([14-15]).
En relación con los proponentes, tres de ellos fueron realizados conjuntamente por profesores y estudiantes de posgrado ([14-1], [14-7] y [1414]), uno por profesores del sistema educativo e integrantes de un grupo de investigación ([14-8]), uno por integrantes de un grupo de investigación ([14-2]), cinco por estudiantes –uno de posgrado ([14-4]), tres de pregrado ([14-10], [14-15] y [1418] y uno con estudiantes de pregrado y posgrado [14-6])– y en ocho casos no fue posible establecer quién los propone ([14-3], [14-5], [14-9], [14-11], [14-12], [14-13], [14-16] y [14-17]). Con respecto a las ciudades donde fueron realizados estos trabajos encontramos: seis en Bogotá ([14-4], [14-6], [14-7], [14-10], [14-15] y [14-18]), tres en Medellín ([14-1], [14-3] y [14-14]), dos en Armenia ([14-2] y [14-5]), uno en Bucaramanga ([14-8]), dos en Cali ([14-9] y [14-11]), uno en Cúcuta y Táchira ([14-17]), uno en San José del Guaviare ([14-13]) y uno en Sincelejo ([14-16]). Además, se reporta uno desarrollado en el municipio de Turbo ([14-12]).
ECME 15 (2014)
En las memorias de este encuentro, identificamos nueve documentos: Parra, Villa (2015) [15-1]; Aponte, Fernández, Vega (2015) [15-2]; Gómez et al. (2015) [15-3]; Duarte, Rendón, Villa (2015) [15-4]; Perdomo, Tafur, Martínez (2015) [15-5]; Chávez, Samboni (2015) [15-6]; Marcillo, Rojas, Villa (2015) [15-7]; González, Muñoz, López (2015) [15-8], y Guerrero, Salas (2015) [15-9]. Seis de ellos con la intención de plantear actividades para ser desarrolladas en el aula con estudiantes de básica y media, por lo que se catalogan de corte práctico [15-2], [15-5], [15-6], [15-7], [15-8] y [15-9]) y dos relacionados con revisiones documentales ([15-1]y [15-3]) y uno con el uso de la MM como herramienta de formación para los ingenieros ([15-4]), por lo que entran en la categoría de teóricos. En cuanto a los trabajos de corte práctico, podemos señalar que se centran en contenidos como la proporcionalidad directa y la función lineal ([15-2] y [15-3]), aspectos sociales que se pueden desarrollar en los estudiantes con el enfoque sociocrítico de la MM ([15-6]), reflexiones de profesores de primaria gracias a la incorporación de la modelación y comunicología ([15-7]). En cuanto a las revisiones documentales, puede observarse que una trata sobre las tendencias de la MM en educación primaria ([15-1]), trabajos desarrollados en el enfoque sociocrítico ([15-3]) y la MM como herramienta de formación para los ingenieros ([15-4]).
De los seis documentos que reportan actividades para ser desarrolladas con estudiantes, cuatro están dirigidos a estudiantes de secundaria ([15-2], [15-5], [15-7] y [15-9], uno a estudiantes de primaria ([156]) y uno a profesores de primaria ([15-8]). Siendo las ciudades donde se desarrollaron estos trabajos: Medellín –cinco– ([15-1], [15-3], [15-4], [15-7] y [15-8]), Bogotá –dos ([15-6], [15-9])–, Cali –uno ([15-1])– y Florencia –uno ([15-5])–. Siete están formulados por estudiantes –de maestría o doctorado ([15-1], [15-2], [15-3], [15-4], [15-7], [15-8] y [15-9])– y sus asesores de tesis y dos solamente por los estudiantes que las desarrollan ([15-5] y [15-6]).
ECME 16 (2015)
Durante la versión 16 del ECME observamos siete documentos: Sierra, Monroy (2016) [16-1]; Sánchez et al. (2016) [16-2]; Botello, Parada (2016) [16-3]; Bolaños, Arboleda, Motato (2016) [16-4]; Cetina, Cabañas, Villa (2016) [16-5]; Romero, Barrios, Gal-vis (2016) [16-6], y Perilla, Mancera, Camelo (2016) [16-7], de los cuales seis tuvieron un corte de carácter práctico ([16-1], [16-3], [16-4], [16-5], [16-6] y [16-7]) y dos que pueden catalogarse como teóricos ([16-2] y [16-6]). En cuanto a los primeros, puede decirse que dan cuenta, por ejemplo, de: la creación y análisis de un ambiente de MM ([166]), propuestas didácticas que buscan fortalecer el pensamiento científico con relación al contenido matemático ([16-4]) y el proceso que los estudiantes desarrollan al modelar algunas situaciones ([16-5]). Mientras que en los documentos de carácter teórico se presentan, por un lado, planteamientos acerca de los alcances y limitaciones que tiene la MM cuando se implementa a través de proyectos ([16-2]), y por otro, se reflexiona sobre aspectos relacionados con la emergencia de discursos desarrollados por los estudiantes cuando se involucran en actividades de MM ([16-6]).
De los siete documentos, tres plantearon actividades para ser desarrolladas en el aula con estudiantes de básica y media ([16-5], [16-6] y [16-7]), tres con estudiantes de pregrado ([16-1], [16-2] y [16-3]) y tan solo en un caso no fue posible identificar la población a la que fue dirigido [16-1]. En cuatro casos no fue posible identificar en qué marco fue desarrollada la experiencia ([16-1], [16-2], [164] y [16-5]), los restantes tres fueron desarrollados en el ámbito de una investigación ([16-3]), de un trabajo de maestría ([16-6]) y de una experiencia de aula ([16-7]). En relación con los proponentes, cuatro de ellos fueron realizados conjuntamente por profesores y estudiantes ([16-1], [16-4], [16-5] y [16-6]) (en tres de ellos no fue posible identificar si los estudiantes eran de pregrado o posgrado), uno por profesores universitarios ([16-2]), uno por profesores universitarios y de colegio ([16-7]), y otro por estudiantes de pregrado y egresados ([16-3]). Las ciudades donde se realizaron estas propuestas son: Bogotá –dos ([16-6] y [16-7])–, Bucaramanga –una ([16-3])–, Cali –una ([16-4])–, Chilpancingo (México) –una ([16-5])– y Medellín –una ([16-2])–. Además, se reporta un trabajo desarrollado en el municipio de Fusagasugá ([16-1]).
c. Etapa de análisis
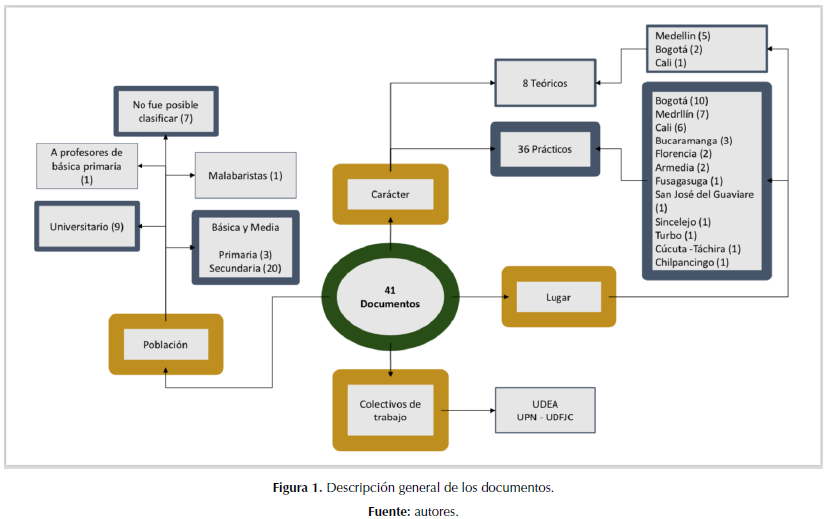
Un primer aspecto que queremos resaltar es que de los 41 documentos analizados, 36 son de carácter práctico y 8 de orden teórico, por lo que podemos señalar que los que hacen algún tipo de alusión a la MM en los últimos cinco años en los ECME, tienen una clara tendencia a cuestiones prácticas –aproximadamente el 88 %–. Circunstancia que deja entrever que la MM en el campo de la educación matemática en Colombia hasta ahora está iniciando un desarrollo teórico propio. Si bien es usual que dichas propuestas de corte práctico retomen un insumo teórico en las experiencias internacionales para ponerlo en práctica en nuestro contexto, es pertinente observar que con el transcurrir de los años la comunidad empieza a mostrar interés en los aspectos teóricos en esta actividad.
En este último sentido, establecimos que los trabajos teóricos son desarrollados en Medellín –cinco–, Bogotá –dos– y Cali –uno–. Se encontraron dos colectivos de trabajo: uno en la Universidad de Antioquia –Medellín– y otro interinstitucional en las universidades Pedagógica Nacional y Distrital Francisco José de Caldas –Bogotá–.
Por su parte, los trabajos prácticos fueron desarrollados en Bogotá (diez), Medellín –siete–, Cali –seis–, Bucaramanga –tres–, Florencia –dos–, Armenia –dos–, Fusagasugá –uno–, San José del Guaviare –uno–, Sincelejo –uno–, Turbo –uno– y dos trabajos con carácter internacional, uno desarrollado en la frontera colombo-venezolana Cúcuta-Táchira, y otro en Chilpancingo (México). Identificamos, además, que el profesor Jhony Villa lidera la mayor cantidad de iniciativas que se presentan en los ECME en torno de la MM.
En cuanto a la población sobre la que se desarrolló el trabajo, la mayoría de documentos estuvieron dirigidos a estudiantes de básica y media, de los cuales tres fueron en primaria y veinte en secundaria; seguidos por nueve universitarios y uno que se desarrolló con malabaristas profesionales, uno dirigido a profesores de básica primaria y en siete documentos no fue posible establecer la población.
En la figura 1, y a manera de resumen, condensamos los anteriores aspectos con el ánimo favorecer un mayor entendimiento.
Conscientes de que nuestro propósito es iniciar y aportar a la comunidad académica una revisión de la literatura sobre el estado de la MM colombiana en los últimos ECME, nos propusimos retomar cada uno de los 41 documentos con el ánimo de identificar aquellos que presentaran explícitamente una definición sobre la MM, así como el desarrollo de esta, pues consideramos interesante ahondar sobre las ideas que en los encuentros rondan sobre esta actividad matemática en cada uno de los ECME.
ECME 13
Para esta versión del ECME pudimos establecer que un documento [13-5] no hace mención a una definición explícita de la MM, ya que tan solo plantea que “se utilizan modelos matemáticos representados por ecuaciones diferenciales de primer orden que describen el fenómeno”, pero no desarrolla más profundamente la idea, dedicando el texto a explicar cómo encontrar soluciones con un software. Los demás documentos sí proporcionan sendas definiciones sobre la MM.
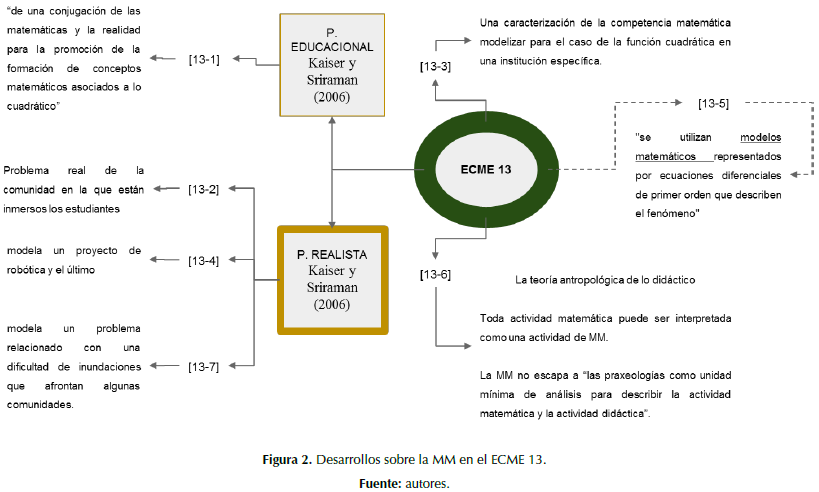
El trabajo [13-1] puede inscribirse dentro de lo que Kaiser, Sriraman (2006) han denominado la perspectiva educacional, pues pretende dar cuenta “de una conjugación de las matemáticas y la realidad para la promoción de la formación de conceptos matemáticos asociados a lo cuadrático” [13-1, p. 265].
En cuanto a los documentos [13-2], [13-4] y [13-7] los caracterizamos como lo que Kaiser, Sriraman (2006) califican como perspectiva realista, pues el primero modela un problema de la vida real de la comunidad en que están inmersos los estudiantes; el segundo modela un proyecto de robótica, y el último, un problema de inundaciones que afrontan algunas comunidades.
En [13-3] se encuentra un desarrollo más cercano a lo que puede entenderse por modelizar que a la propia MM, pues este trabajo pretende establecer cuál caracterización de la competencia matemática modelizar para el caso de la función cuadrática en una institución específica.
Por su parte [13-6] se basa en la teoría antropológica de lo didáctico, aceptando que toda actividad matemática puede ser interpretada como una actividad de MM, por lo que esta última no escapa a “las praxeologías como unidad mínima de análisis para describir la actividad matemática y la actividad didáctica”.
En la figura 2, representamos los desarrollos vislumbrados sobre la MM en el ECME 13.
ECME 14
En esta versión del ECME consideramos que los documentos [14-8] y [14-11] merecen una mención aparte. El primero se centra en un análisis de contenido de libros de texto –de grado décimo– y en las actividades propuestas para el estudio de las relaciones trigonométricas. El segundo se enfoca en presentar reflexiones “frente al papel que desempeña la integración de la Teoría Antropológica de lo Didáctico (TAD) y la Génesis Instrumental en dos experiencias investigativas con el uso de las calculadoras graficadoras algebraicas, CBR (Calculator Based Ranger) y/o Lápiz/Papel (L/P)". Ninguno aborda, decisivamente, la idea de MM, circunstancia que nos llevó a no considerarlos en esta fase del análisis.
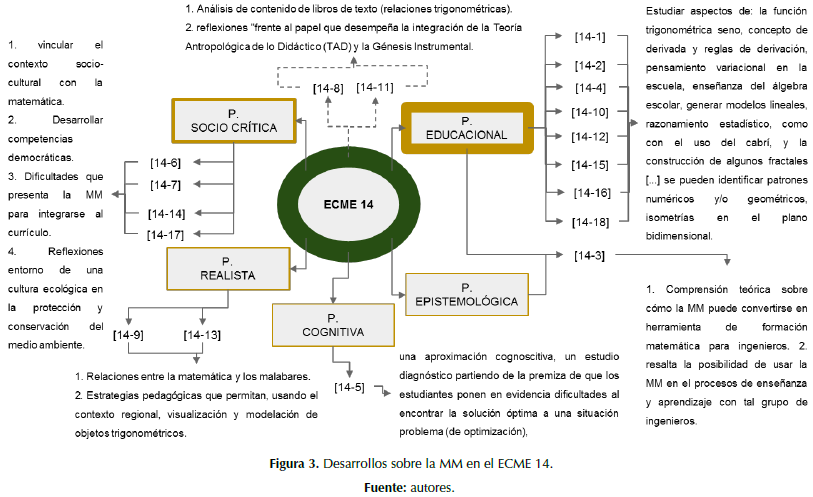
En relación con los documentos [14-1], [14-2], [14-4], [14-10], [14-12], [14-15] [14-16] y [14-18], los clasificamos en la perspectiva educacional. Pues en [14-1] se presentan resultados parciales de una investigación en la que se sugirió un proceso de MM para estudiar algunos aspectos de la función trigonométrica seno; mientras que en [14-2], los autores buscan determinar la diferencia en el aprendizaje significativo del concepto de derivada y reglas de derivación, en dos grupos de cálculo diferencial con estudiantes universitarios. En [14-4], el autor concluye, en relación con el estudio del pensamiento variacional en la escuela, que este debe surgir de tareas sobre las nociones de cambio, variaci y procesos de MM, en busca de desarrollos por comprensión y no como un estudio formal de conceptos. Por su parte, en [14-10] se esboza una propuesta para la enseñanza del álgebra escolar, para ello, sugieren que el docente inicie dicha enseñanza con un lenguaje retórico, seguido del sincopado y del simbólico; considerando como un hecho importante que el docente plantee situaciones donde el estudiante modele problemas algebraicos en un lenguaje que esté en concordancia con el momento en que se encuentre. En [14-12] se presentan resultados de una investigación desarrollada en una institución rural de la región de Urabá, con el propósito de analizar un proceso de MM que les permitiera a los estudiantes generar modelos lineales desde un análisis del cultivo del plátano. En [14-15], “se reportan los resultados de una secuencia de actividades que tiene por finalidad potenciar el desarrollo de razonamiento estadístico en estudiantes de quinto de primaria como medio para la construcción de predicciones respecto a la resistencia física”. En [14-16] se presenta un taller cuyo propósito fue “mostrar cómo con el uso del Cabrí, y la construcción de algunos fractales [...] se pueden identificar patrones numéricos y/o geométricos” en el proceso de transición de la aritmética al álgebra. Por último, en [14-18] los autores presentan un proyecto de innovación pedagógica que se centra en la enseñanza/aprendizaje de las isometrías en el plano bidimensional, y reflexionan sobre el desarrollo de una experiencia en los grados sexto y séptimo, donde el arte gráfico posibilita modelar usando las teselaciones.
Al documento [14-3] lo hemos clasificado, por una parte, en la perspectiva epistemológica, por cuanto sus autores buscan informar algunos aspectos que se vienen adelantando en una investigación correspondiente a la formación doctoral, en la que discuten una comprensión teórica sobre cómo la MM puede convertirse en una herramienta de formación matemática para los ingenieros –particularmente de ingeniería de diseño–; y por otra, puede ubicarse en la perspectiva educacional pues pretende resaltar la posibilidad de usar la MM para dar cuenta de los procesos de enseñanza y aprendizaje con tal grupo de ingenieros.
De otro lado, [14-5] se clasifica en la perspectiva cognitiva, pues presenta, desde lo que los mismos autores denominan, una aproximación cognoscitiva, un estudio diagnóstico partiendo de la premisa de que los estudiantes ponen en evidencia dificultades para encontrar la solución optima a una situación problema –de optimización–, las cuales radican en la formulación del modelo matemático y los conocimientos previos propios del calculo.
Los documentos que asumen a la MM desde una perspectiva sociocrítica son: [14-6], [14-7], [14-14] y [14-17]. En el primero, las autoras, al considerar una propuesta para visualizar procesos de MM usados por estudiantes de noveno grado de un colegio público de Bogotá, se enmarcan en esta perspectiva considerando que permite, por una parte, “vincular el contexto sociocultural en el cual están inmersos los estudiantes con la matemática”, y por otra, “como lo menciona Valero (2002) el desarrollo de competencias democráticas necesarias para ser actores responsables en su sociedad”. Por su parte [14-7], al describir los procedimientos realizados en el montaje de un escenario de MM, evidencian dificultades que presenta la MM para integrarse al currículo de matemáticas del grado octavo y formar parte de las prácticas en la clase de matemáticas. En [14-14], los autores analizan la experiencia de modelación del cultivo del café, en cinco estudiantes de grado décimo de una institución educativa ubicada en un municipio reconocido por su producción cafetera. En [14-17] se describe “la producción de etanol a partir de desechos orgánicos domésticos y hojarasca, utilizando modelos matemáticos aplicados en los programas Derive 6.1 y Excel”, a través de la que se reflexiona sobre una cultura ecológica en la protección y conservación del medio ambiente.
En relación con la perspectiva realista, encontramos los documentos [14-9] y [14-13]. En el primero se exhiben, concretamente, las relaciones entre la matemática y los malabares; y menciona que la manera de modelizar matemáticamente los lanzamientos, por ejemplo, recibe el nombre de transposicionales, en las cuales el tiempo entre los lanzamientos es constante, lo cual da lugar a calcular el número de lanzamientos posibles desde que se proyecta la bola hasta que regresa. Entre tanto, el segundo expone y reflexiona acerca de una estrategia pedagógica para proveer herramientas a los estudiantes de decimo grado que les permitan, usando el contexto regional, la visualización y modelación de objetos trigonométricos.
En la figura 3, de forma sintética, presentamos los desarrollos encontrados sobre la MM en el ECME 14.
ECME 15
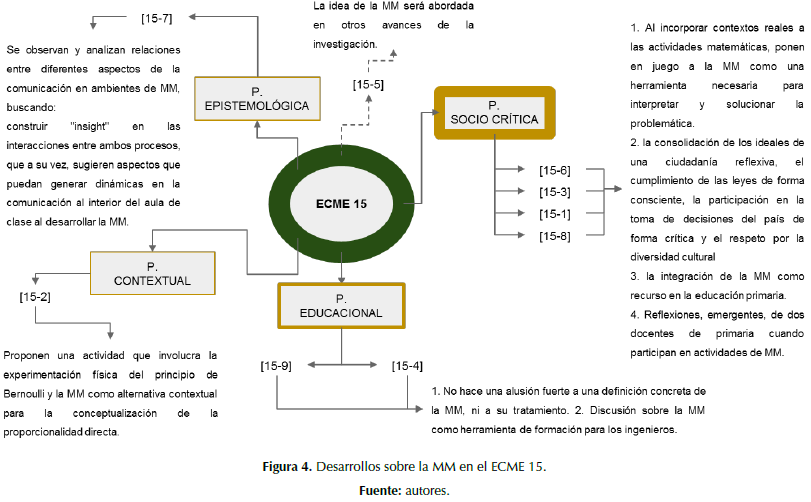
En esta versión del ECME excluimos el documento [15-5] dado que los propios autores señalan que la idea de la MM será abordada en otros avances de la investigación. De los ocho documentos restantes, cuatro de ellos –[15-6], [15-3], [15-1] y [15-8]– hacen alusión a lo que podemos denominar MM desde una perspectiva sociocrítica. En el primero de ellos, al incorporar contextos reales a las actividades matemáticas, las autoras ponen en juego a la modelación como una herramienta necesaria tanto para interpretar como para solucionar la problemática que le da vida a la actividad. En el segundo, los autores consideran que la MM puede ayudar a la finalidad de “la consolidación de los ideales de una ciudadanía reflexiva, el cumplimiento de las leyes de forma consciente, la participación en la toma de decisiones del país de una forma crítica y el respeto por la diversidad cultural”. Cabe señalar que a diferencia del anterior, presenta en su desarrollo una relación clara con esta perspectiva, pero no explicita una definición concreta de lo que significa para ellos la MM desde dicha perspectiva. En el tercer documento, los autores indagan por la integración de la MM como un recurso en la educación primaria, mientras que en el cuarto centran su atención en las reflexiones, emergentes, de dos docentes de primaria cuando participan en actividades de MM.
De los documentos clasificados en la perspectiva educacional, [15-9] y [15-4], el primero no hace una alusión fuerte a una definición concreta de la MM, ni al tratamiento de la modelación a lo largo del documento. Esta situación es opuesta a la del segundo documento, en el que se presenta una discusión sobre la MM como herramienta de formación para los ingenieros.
En relación con el documento [15-7], se observan y analizan relaciones entre diferentes aspectos involucrados de la comunicación en ambientes de MM; con lo que se busca construir insight en las interacciones entre ambos procesos, que a su vez, sugieren aspectos que puedan generar dinámicas en la comunicación en el interior del aula de clase al desarrollar la MM. Esta circunstancia, a nuestro modo de ver, enfatiza en el desarrollo de la teoría interna de la modelación, por lo que la clasificamos en la perspectiva epistemológica en un sentido más amplio del propuesto por Kaiser, Sriraman (2006), pues su tratamiento no es sobre conceptos y propiedades matemáticas.
Finalmente, en el documento [15-2], inscrito en la perspectiva contextual, se propone una actividad que involucra la experimentación física del principio de Bernoulli y la MM como alternativa contextual para la conceptualización de la proporcionalidad directa.
En la figura 4, presentamos los desarrollos observados sobre la MM en el ECME 15.
ECME 16
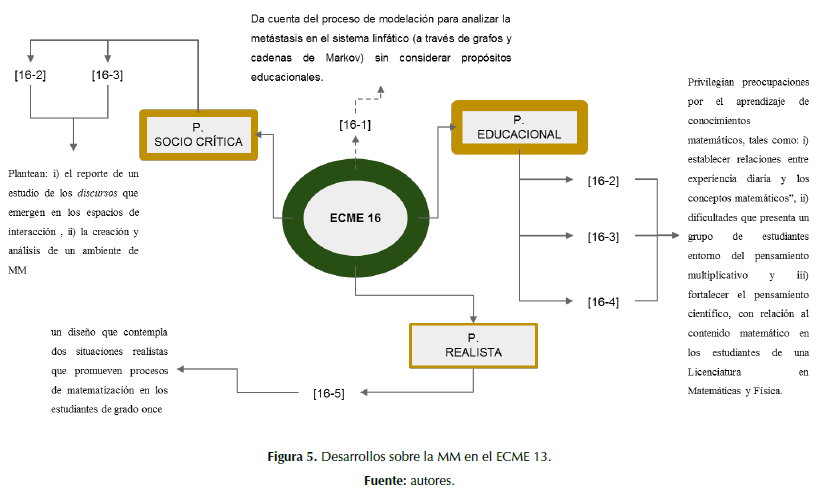
En este encuentro hemos establecido que, de los siete documentos analizados, uno ([16-1]) no se inscribe en la educación matemática, ya que da cuenta del proceso de modelación desarrollado para analizar la metástasis en el sistema linfático, a través de grafos y cadenas de Markov, sin tomar en consideración propósitos educacionales en la construcción del modelo. Los restantes seis sí son de interés para el campo de la educación matemática.
Así, [16-2], [16-3] y [16-4] son documentos que se pueden catalogar en la perspectiva educacional, por cuanto sus objetivos privilegian preocupaciones por el aprendizaje de conocimientos matemáticos, pues [16-2] parte por reconocer a “la modelación matemática como un recurso que permite establecer relaciones entre experiencia diaria y los conceptos matemáticos”; [16-3] sugiere identificar, a través de una prueba diagnóstico, cuáles son las dificultades de un grupo de estudiantes en torno del pensamiento multiplicativo; mientras que [16-4] esboza una herramienta didáctica que pretende fortalecer el pensamiento científico, con relación al contenido matemático en los estudiantes de una licenciatura en Matemáticas y Física.
En la perspectiva teórica de la educación matemática realista pudimos identificar a [16-5], pues reportó la exploración de “un diseño que contempla dos situaciones realistas que promueven procesos de matematización en los estudiantes de grado once”.
Por su parte, [16-6] y [16-7] explicitan una perspectiva sociocrítica de la MM: el primero muestra el reporte de un estudio de los discursos que emergen en los espacios de interacción constituidos durante un proceso de MM; mientras que el segundo se propone reportar la creación y análisis de un ambiente de MM desde la perspectiva mencionada.
En la figura 5, presentamos los desarrollos percibidos sobre la MM en el ECME 16.
3. A manera de conclusión
Partimos por reconocer la importancia que fue adquiriendo la MM en nuestras prácticas pedagógicas e investigativas en educación matemática, por lo que identificamos una ausencia en la organización de los trabajos desarrollados en Colombia en torno a dicha idea. Nos propusimos, entonces, de manera general, desarrollar un estudio que nos ayudará a plantear un panorama de lo que hasta hoy se ha realizado en la MM en el país, inspirados en el epígrafe de este documento. Observamos, además, que un trabajo en esa dirección significa un esfuerzo de largo aliento, por lo que decidimos realizar una revisión de los trabajos que se desarrollaron en los últimos cuatro Encuentros Colombianos de Matemática Educativa. Para ello seleccionamos, estructuramos y analizamos los documentos que hacen referencia a la MM en los últimos cuatro encuentros desarrollados.
Identificamos que los trabajos se encapsulan en ocho perspectivas: educacional –34,1 %–, socio-crítica –24,4 %–, realista –14,6 %–, epistemológica –4,9 %–, cognitiva –2,4 %–, contextual –2,4 %–, teoría antropológica de lo didáctico –2,4 %– y modelizar –2,4 %–. Es importante resaltar que cinco trabajos –12,1 %– no se analizaron porque consideramos que no se enmarcan en la educación matemática. Como puede apreciarse, se evidencia una pluralidad en las perspectivas educacional, sociocrítica y relista, lo que contrasta con las restantes, pues son reducidas y esporádicas. Esta situación permite señalar que la MM, en los eventos analizados, tiene un desarrollo eminentemente didáctico, práctico y que su avance teórico es circunstancial. Lo anterior se reafirma al observar que, de los documentos analizados, 31 son de corte práctico, mientras tan solo 8 son de carácter teórico.
En cuanto a las líneas de preocupación podemos identificar que existe un énfasis en el desarrollo de trabajos que plantean a la MM como medio para la enseñanza o aprendizaje de contenidos específicos; seguido de una preocupación por utilizarla para el fomento de algún tipo de pensamiento crítico, siendo las actividades o problemas planteados desde contextos realistas. Tan solo un documento –de un avance doctoral–permite una conexión entre dos de estas perspectivas –epistemológica y educacional–.
Los trabajos en general proceden de las ciudades de Bogotá –doce–, Medellín –doce– y Cali –siete–, lo que permite identificar que esta actividad se concentra en las principales ciudades capitales del país; y son dirigidos en su mayoría a estudiantes de básica y media, seguidos por trabajos cuyo interés está a nivel universitario.
A la luz de lo anterior, esta revisión nos permite preguntarnos sobre la producción académica que pudiera estar aconteciendo en los municipios apartados de las capitales, pues –al menos en estos eventos– no se observan tales iniciativas. Este hecho nos motiva a hacer un llamado a la comunidad de educadores matemáticos para generar canales que nos permitan conocer, de primera mano, los desarrollos que allí se estén consolidando y desde tal reconocimiento avanzar en la construcción de colectivos de trabajo alrededor de la MM. Así mismo, y dada la escasa producción reportada, cabe cuestionarse si lo que se divulga en los eventos sobre lo que acontece en ciudades como Bogotá, Medellín y Cali es representativo de lo que allí se desarrolla en la MM.
En relación con las conexiones entre los trabajos reportados, es necesario resaltar que se evidencia poco reconocimiento entre los investigadores nacionales, pues no se recogen suficientemente los desarrollos que se van decantando. Sin embargo, en al menos dos colectivos de trabajo se adoptan marcos teóricos comunes que provienen de investigadores reconocidos a nivel internacional. Lo anterior puede darse porque parte de la producción se centra en la elaboración de trabajos de posgrado a los que no se les da mayor continuidad una vez que los estudiantes se gradúan. No obstante, es importante reconocer, en tales colectivos, el surgimiento de producción académica propia.
Por último, somos conscientes de que esta exploración resulta ser una pequeña muestra en nuestro intento de narrar lo que sucedi para, a partir de allí, atrevernos a proyectar el trabajo que debemos desarrollar. En ese sentido, una de las preocupaciones que queremos resaltar, derivada de este estudio inicial, tiene que ver con la interpretación que, tal vez, se le esté dando en las aulas colombianas a las prácticas de MM, por lo que invitamos a la comunidad académica a aunar esfuerzos con tal propósito.
4. Agradecimientos
Queremos agradecer especialmente a las profesoras Claudia Salazar y Diana Acevedo, por sus profundas lecturas y aportes en la construcción de este documento. Así mismo, a los egresados tanto del grupo de investigación EdUtopía como del colectivo de Edumays, por sus valiosas consideraciones. No obstante, las afirmaciones e ideas desarrolladas en este texto son enteramente de nuestra responsabilidad.
Notas al pie de página
1 . Si partimos de su incorporación en el currículo colombiano a través del documento de los Lineamientos, este proceso lleva alrededor de dos décadas de desarrollo.
2 . Las memorias de los eventos están disponibles en la página web http://asocolme.org/publicaciones-asocolme/memorias-ecme.
3 . Para comodidad al referenciar los documentos que analizamos, los codificamos de acuerdo con el Encuentro en que fue presentado y a su aparición en la publicación de las memorias. Así, por ejemplo, Henao, Vanegas (2012) se corresponde con el código [13-1], pues fue presentado en el 13 Encuentro Colombiano de Matemática Educativa y es el primer documento de ese encuentro que hace referencia a la MM.
Referencias bibliográficas
ÁLVAREZ, D.; COLORADO, H.; OSPINA, P. Una propuesta didáctica para la enseñanza del concepto de derivada. Revista Científica, Bogotá, v. 1, n. esp., pp. 95-101. 2013. https://doi.org/10.14483/23448350.5961
APONTE, H.; FERNÁNDEZ, J.; VEGA, M. (2015). Modelación matemática a través de fenómenos físicos. La proporcionalidad directa y el principio de Bernoulli. RECME, Bogotá, v. 1, n. 1, pp. 348-352. 2015.
APONTE, P.; ALMÉCIGA, H.; TORRES, D. Apuntes para la enseñanza de objetos matemáticos inmersos en el álgebra escolar. Un paso por diversas investigaciones. Revista Científica, Bogotá, v. 1, n. esp., pp. 345-350. 2013. https:// doi.org/10.14483/23448350.7071
ARAÚJO, J. Uma Abordagem Sócio-Crítica da Modelagem Matemática: a perspectiva da educação matemática crítica. ALEXANDRIA Revista de Educação em Ciência e Tecnologia, Florianópolis, Brasil, v. 2, n. 2, pp. 55-68, 2009.
ARENDT, H. La condici humana. 1993. Disponible en: http://www.perio.unlp.edu.ar/catedras/sites/default/files/arendt_h_-_la_condicion_humana_prologo_byn.pdf.
BARBOSA, J. Mathematical modelling in classroom: A socio-critical and discursive perspective. ZDM, Alemania, v. 38, n. 3, pp. 293-301, 2006. https://doi.org/10.1007/BF02652812
BOLAÑOS, J; ARBOLEDA, C.; MOTATO, J. (2016). Sistematización de una experiencia para la enseñanza del movimiento parabólico y su relación con el modelo termodinámico: una vía para fortalecer el pensamiento científico en los estudiantes de Licenciatura en matemáticas y física de Universidad del Valle. Revista Colombiana de Matemática Educativa, Bogotá, v. 1, n. 1b, p. 150. 2016.
BOSSIO, J.; LONDOÑO, S.; JARAMILLO, C. Modelación matemática en el aula clase: una producción de modelos lineales desde el contexto del cultivo de plátano. Revista Científica, Bogotá, v. 1, n. esp., pp. 409-412. 2013. https://doi.org/10.14483/23448350.6507
BOTELLO, I.; PARADA, S. La evaluación del Pensamiento Variacional de los estudiantes de recién ingreso a la Universidad. Revista Colombiana de Matemática Educativa, Bogotá, v. 1, n. 1b, p. 146. 2016.
BUSTOS, A.; BUSTOS, G.; NOVOA, Y. Propuesta de ambientes de aprendizaje para la promoción de la modelación matemática desde la perspectiva crítica. Revista Científica, Bogotá, v. 1, n. esp., pp. 95-101. 2013.
CETINA, M.; CABAÑAS, G.; VILLA, J. Situaciones realistas y la matematización de la función cuadrática. Revista Colombiana de Matemática Educativa, Bogotá, v. 1, n. 1b, pp. 151-152. 2016.
CHÁVEZ, A.; SAMBONI, T. No le des la espalda a tu espalda. Cuidado del cuerpo y matemáticas. RECME, Bogotá, v. 1, n. 1, pp. 369-374. 2015.
COLOMBIA. Ministerio de Educación Nacional. Lineamientos curriculares. Área Matemáticas. Cooperativa Editorial del Magisterio, Bogotá: Colombia. 1998.
CUMBAL, L. La modelación matemática como proceso de estudio en el álgebra escolar. En: 13 ENCUENTRO COLOMBIANO DE MATEMÁTICA EDUCATIVA. Medellín: Colombia. 2012.
DUARTE, P.; RENDÓN, P.; VILLA, J. La modelación matemática: una experiencia de formación en ingeniería. RECME, v. 1, n. 1, pp. 440-445. 2015.
ECHEVERRY, F.; AUDOR, Y. La matemática en los malabares. Revista Científica, Bogotá,
v. 1, n. esp., pp. 303-307. 2013. https://doi.org/10.14483/23448350.7059
ESPINOSA, J. Solución de modelos matemáticos, utilizando el software Derive 6.1 en aplicaciones de ecuaciones diferenciales de primer orden. En: 13 ENCUENTRO COLOMBIANO DE MATEMÁTICA EDUCATIVA. Medellín: Colombia. 2012
ESPINOSA, J.; HERNÁNDEZ, H.; YÁÑEZ, L. Descripción de la producción de etanol a partir de desechos orgánicos domésticos y hojarasca, utilizando modelos matemáticos aplicados en el software Derive 6.1 y la hoja de cálculo Excel. Revista Científica, Bogotá,
v. 1, n. esp., pp. 700-704. 2013. https://doi.org/10.14483/23448350.7755
GALÁN, G.; RODRÍGUEZ, Y. Dibujando la realidad usando las Isometrías en el plano bidimensional. Revista Científica, Bogotá, v. 1, n. esp., pp. 709-711. 2013. https://doi.org/10.14483/23448350.7757
GALLEGO, L.; ALDANA, E. Análisis de la concepción de la actividad de optimizar, desde una ingeniería didáctica. Revista Científica, Bogotá, v. 1, n. esp., pp. 216-219. 2013. https://doi.org/10.14483/23448350.6486
GÓMEZ, O. Desarrollo del pensamiento variacional en estudiantes de grado noveno. Revista Científica, Bogotá, v. 1, n. esp., pp. 115-120. 2013. https://doi.org/10.14483/23448350.5966
GÓMEZ, P. et al. Aspectos sociocríticos en la modelación matemática: una revisión documental. RECME, Bogotá, v. 1, n. 1, pp. 353-358. 2015.
GONZÁLEZ, S.; MUÑOZ, L.; LÓPEZ, C. Reflexiones docentes a partir de actividades de modelación matemática. RECME, Bogotá, v. 1, n. 1, pp. 399-403. 2015.
GUERRERO, F.; SALAS, J. Narrativas de los derechos humanos en educación matemática: el caso de los estudiantes de grado sexto. RECME, Bogotá, v. 1, n. 1, pp. 451-455. 2015.
HENAO, S. M.; VANEGAS, J. A. La modelación matemática en la educación matemática realista: un ejemplo a través de la producción y uso de modelos cuadráticos. En: 13 ENCUENTRO COLOMBIANO DE MATEMÁTICA EDUCATIVA. Medellín: Colombia. 2012.
HERNÁNDEZ, E.; CUEVAS, J. Razonamiento estadístico en estudiantes de quinto de primaria a partir de predicciones en torno a la idea de resistencia física. Revista Científica, Bogotá,
v. 1, n. esp., pp. 551-554. 2013. https://doi.org/10.14483/23448350.7723
KAISER, G.; SRIRAMAN, B. A global survey of international perspectives on modelling in mathematics education. ZDM, v. 38, n. 3, pp. 302-310. 2006. https://doi.org/10.1007/BF02652813
MARCILLO, A.; ROJAS, C.; VILLA, J. Procesos de comunicación en la modelación matemática escolar. RECME, Bogotá, v. 1, n. 1, pp. 392398. 2015.
MARTÍNEZ, D., PÁEZ, O.; GARCÍA, G. Modelación desde la perspectiva de la educación matemática crítica. Cuestiones relacionadas con la obsolescencia. Revista Científica, Bogotá, v. 1, n. esp., pp. 288-292. 2013. https://doi.org/10.14483/23448350.7054
MOLINA, J.; VILLA, J. La modelación en la producción de conocimiento matemático: el caso de la función seno. Revista Científica, Bogotá, v. 1, n. esp., pp. 80-84, 2013. https://doi.org/10.14483/23448350.5496
MOLLOGÓN, J. Un problema de alturas en el Guaviare. Revista Científica, Bogotá, v. 1, n. esp., pp. 523-527. 2013.
MORENO, J. La modelación matemática en el contexto de la robótica: una actividad didáctica realizada por aprendizaje de proyectos para el concepto de proporción. En: 13 ENCUENTRO COLOMBIANO DE MATEMÁTICA EDUCATIVA. Medellín: Colombia. 2012.
OBANDO, J.; SÁNCHEZ, J.; MUÑOZ, L.; VILLA, J. El reconocimiento de variables en el contexto cafetero y su constitución como modelos matemáticos. En: 13 ENCUENTRO COLOMBIANO DE MATEMÁTICA EDUCATIVA. Medellín: Colombia. 2012.
OLMOS, C.; SARMIENTO, D.; MONTEALEGRE E. Competencia matemática modelizar: un estudio exploratorio desde la función cuadrática. En: 13 ENCUENTRO COLOMBIANO DE MATEMÁTICA EDUCATIVA. Medellín: Colombia. 2012.
PARRA, M.M.; VILLA, J. Tendencias en investigación en modelación matemática en educación primaria. RECME, Bogotá, v. 1, n. 1, pp. 235240. 2015.
PEDREROS, M.; MEJÍA, M. Relaciones e integraciones de la Teoría Antropológica de lo Didáctico y la Génesis Instrumental. Revista Científica, Bogotá, v. 1, n. esp., pp. 397-401. 2013.
PERDOMO, E.; TAFUR, Y.; MARTÍNEZ, J. La conversión entre los registros de representación de la función lineal y criterios de congruencia entre algunas de sus representaciones. RECME, Bogotá, v. 1, n. 1, pp. 72-77. 2015.
PERILA, W.; MANCERA, G.; CAMELO, F. La telefonía móvil en Colombia: un ambiente de modelación matemática desde una perspectiva crítica. RECME, Bogotá, v. 1, n. 1b, pp. 100-101. 2016.
PLANAS, N.; VALERO, V. Tracing the socio-cultural-political axis in understanding mathematics education. En BOERO, P.; LEDER, G. (eds.). The Second Handbook of the Psychology of Mathematics Education. The journey continues. Sense Publishers. Róterdam: Países Bajos. 2016. pp. 447-449. https://doi.org/10.1007/978-94-6300-561-6_13
PUERTO J. El uso de los fractales para potenciar el desarrollo del pensamiento algebraico-variacional a través del software Cabrí “Del pensamiento numérico al pensamiento Algebraico-Variacional”. Revista Científica, Bogotá, v. 1, n. esp., pp. 665-669. 2013. https:// doi.org/10.14483/23448350.7747
RENDÓN, P.; ESTEBAN, P; VILLA. J. La modelación matemática en la ingeniería de diseño. Revista Científica, Bogotá, v. 1, n. esp., pp. 102-106. 2013. https://doi.org/10.14483/23448350.5962
RIVERA, S.; LONDOÑO, S.; JARAMILLO, O. Medida de área y el volumen en contextos auténticos: una alternativa de aprendizaje a través de la modelación matemática. En: 13 ENCUENTRO COLOMBIANO DE MATEMÁTICA EDUCATIVA. Medellín: Colombia. 2012
ROMERO, J.; BARRIOS, O.; GALVIS, T. Emergencia de discusiones en un proceso de modelación matemática desde la perspectiva sociocrítica. Revista Colombiana de Matemática Educativa, Bogotá, v. 1, n. 1b, p. 156. 2016.
SÁNCHEZ, J. et al. Posibilidades y limitaciones de la Modelación Matemática a través de proyectos. Una experiencia en formación inicial de profesores. RECME, Bogotá, v. 1, n. 1b, pp. 130131. 2016.
SÁNCHEZ, J.; OBANDO, J.; MUÑOZ, L.; VILLA, J. La modelación matemática: Un ejemplo en el contexto cafetero. Revista Científica, Bogotá, v. 1, n. esp., pp. 474-478. 2013. https://doi.org/10.14483/23448350.6570
SIERRA, L.; MONRROY, N. Análisis de la metástasis en el sistema linfático, con grafos y cadenas de Markov. Revista Colombiana de Matemática Educativa, Bogotá, v. 1, n. 1b, p. 86. 2016.
TAVERA, F.; VILLA, J. El pensamiento variacional en el estudio de las relaciones trigonométricas: una mirada desde los libros de texto. Revista Científica, Bogotá, v. 1, n. esp., pp. 298-302. 2013. https://doi.org/10.14483/23448350.7058
VALERO, P. Consideraciones sobre el contexto y la educación matemática para la democracia. Quadrante, Portugal, v. 11, n. 1, p. 33–40, 2002.
License
Gondola, Ens Aprend Cienc. is an open-access publication, free of charge for authors and readers. The publication, consultation or download of the contents of the magazine does not generate any cost for the authors or the readers, since the Francisco José de Caldas District University assumes the expenses related to edition, management and publication. The peer evaluators do not receive any economic retribution for their valuable contribution. The work of all the actors mentioned above is understood as a contribution to the strengthening and growth of the research community in the field of Science Education.
As of December 1, 2018 the contents of the journal are published under the terms of the Creative Commons License Attribution-Noncommercial- ShareAlike 4.0 International (CC-BY-NC-SA 4.0), under which others may distribute, remix, retouch, and create from the work in a non-commercial way, give credit and license their new creations under the same conditions.
The copyright holders are the authors and the journal Gondola, Ens Aprend Cienc. The holders retain all rights without restrictions, respecting the terms of the license in terms of consultation, downloading and distribution of the material.
When the work or any of its elements is in the public domain according to the applicable law in force, this situation will not be affected by the license.
Likewise, we encourage authors to deposit their contributions in other institutional and thematic repositories, with the certainty that culture and knowledge is a good of all and for all.




















