PROCESOS APLICADOS POR LOS ESTUDIANTES EN LA RESOLUCIÓN DE PROBLEMAS MATEMÁTICOS: ESTUDIO DE CASO SOBRE LA FUNCIÓN CUADRÁTICA

PROCESSES APPLIED BY STUDENTS TO SOLVE MATHEMATICAL PROBLEMS: CASE STUDY ABOUT QUADRATIC FUNCTION 

PROCESSOS APLICADOS PELOS ALUNOSNARESOLUÇÃO DE PROBLEMAS MATEMÁTICOS: ESTUDO DE CASO COM A FUNÇÃOQUADRATICA

Jhon Herminson Arias-Rueda*, César Augusto Arias-Rueda** y Carlos Arturo Burgos Hernández***

Cómo citar este artículo: Arias-Rueda, J. H., Arias-Rueda, C. A. y Burgos Hernández, C. A. (2020). Procesos aplicados por los estudiantes en la resolución de problemas matemáticos: caso de estudio sobre la función cuadrática. Gdola, ensenza y aprendizaje de las ciencias, 15(2), 284-302. DOI: http://doi.org/10.14483/23464712.14614

Recibido: 11 de marzo de 2019; aprobado: 28 de junio de 2019 

* Magister Scientiarum en Matemática mención Docencia, Universidad del Zulia (Venezuela). Licenciado en Educación mención Matemática y Física. Docente de la Universidad Politécnica Salesiana del Ecuador. Correo electrónico: jariasr@ups.edu.ec

** Doctor en ciencias de la educación, Universidad Rafael Urdaneta (Venezuela). MagisterScientiarum en informática educativa. Licenciado en Educación mención Matemática y Física. Docente de la Unidad Educativa Jean-JacquesRousseau del Ecuador. Correo electrónico: cesaraugustoariasr@gmail.com

*** Magister Scientiarum en matemática mención docencia, Universidad del Zulia (Venezuela). Licenciado en educación mención matemática y física. Docente del Colegio de La Salle Bogotá. Correo electrónico: cburgos85@hotmail.com 

Resumen 

Se presenta una investigación en donde se analizan los procesos que aplica un grupo de estudiantes de Bachillerato durante la resolución de problemas matemáticos, en torno al estudio de las funciones cuadráticas. La teoría que sustentó el trabajo fue el aprendizaje significativo desde la perspectiva ausubeliana. La metodología de esta investigación fue de tipo descriptivo-cuantitativo, enmarcada dentro de un diseño no experimental de tipo transeccional descriptivo. Los datos se recabaron de una muestra de 38 estudiantes que fue tomada mediante una técnica de muestreo no probabilístico, y a la cual se le aplicaron dos instrumentos: un cuestionario y una entrevista semiestructurada. El cuestionario constó de cuatro situaciones problema cuyas soluciones podían encontrarse haciendo uso de las funciones cuadráticas, mientras la entrevista estuvo conformada por trece preguntas semiestructuradas que permitieron complementar la información recabada en el cuestionario. Los resultados evidenciaron que los estudiantes tienden a adquirir un proceso de aprendizaje mecánico y memorístico, dejando a un lado el proceso de reflexión que les permita diseñar una estrategia adecuada para resolver un problema relacionado con las funciones. En conclusión, consideramos que es necesario que los docentes apliquen estrategias de enseñanza/aprendizaje que estimulen la recurrencia a los conocimientos previos del estudiante con el fin de obtener un aprendizaje significativo.

Palabras clave: proceso de aprendizaje; estrategia de aprendizaje; memorización; matemática; función. 

Abstract 

This is an investigation where the processes applied by a group of high school students during the resolution of mathematical problems are analyzed, around the study of quadratic functions.  The theory that supported the work was significant learning from the Ausubelian perspective. We work based on descriptive-quantitative methodology, framed within a non-experimental design of descriptive transectional type. Data was collected with 38 students using a non-probabilistic sampling technique, and applying two instruments: a questionnaire and a semi-structured interview. The questionnaire had four problem situations whose solutions could be found using quadratic functions, while the interview was made up of thirteen semi-structured questions that allowed complementing the information gathered. Results show us that students tend to acquire a process of mechanical and memorial learning, leaving aside the reflection process that allows them to design an appropriate strategy to solve a problem related to functions. In conclusion, teachers must apply teaching-learning strategies that stimulate the recurrence of the student's prior knowledge to obtain meaningful learning.

Keywords: learning process; learning strategy; memorization; mathematics; function. 

Resumo 

Apresnetamos resultados de uma pesquisa na qual analizamos os procesos que desenvolve uma turma de alunos de ensino meio, enquanto resolvem problemas matemáticos, especificamente com funções quadráticas. A teoria que fundamentou nosso trabalho é a aprendizagem significativa desde a perspectiva Ausubeliana. A metodologia de pesquisa foi de tipo descritiva-quantitativa, dentre de um planejamento não experimental de tipo transeccional descritivo. Os dados foram coletados com uma amostra de 38 alunos mediante a técnica de amostra no-probabilistica, para o qual se aplicaram dois instrumenteos: um questionário e uma entrevista semi-estruturada. O questionário teve quatro situações problema cujas soluções podiam ser encontradas fazendo uso das funções quadráticas, enquanto a entrevista foi conformada com treze perguntas semiestruturadas que permitiram complementar a informação. Os resultados evidenciam que os alunos tendem a memorizar um processo mecânico para sua aprendizagem na solução de problemas, deixando de refletir para ganhar verdadeira compreensão do que significa resolver um problema baseado na função quadrática. Em conclusão, consideramos que é necessário que os professores apliquem estratégias de ensino e de aprendizagem que estimule a aprendizagem significativa e que considere os conhecimentos prévios dos estudantes.

Palavras-chave: processo de aprendizagem; estratégia de aprendizagem; memorização; matemática; função. 

Introducción

Este artículo tiene como objetivo divulgar una investigación que pretende reconocer los procesos que aplican los estudiantes de bachillerato, durante la resolución de problemas matemáticos, tomando como objeto matemático de estudio las funciones cuadráticas. Para esto, se hace un análisis de las características del aprendizaje que adquieren los alumnos durante el desarrollo de las clases, fundamentado en la teoría de aprendizaje significativo de Ausubel, y a partir de ello, se recomiendan algunas acciones estratégicas que faciliten a los estudiantes una interpretación correcta de las funciones cuadráticas.

Con la intención de conocer los procesos que aplican los estudiantes al momento de resolver un problema, se ha realizado este estudio de tipo descriptivo que puede servir de fundamento para diseñar estrategias didácticas facilitadoras en el proceso de enseñanza/ aprendizaje, considerando dificultades presentes en el sistema educativo como métodos inapropiados de enseñanza, o bien, problemas relacionados con el desarrollo cognitivo del alumno (Díaz et al., 2014) que en muchos casos puede ser debido a la falta de estrategias de enseñanza que se enfoquen en los procesos de aprendizaje. En concordancia con esto, es importante recalcar que muchos investigadores han obtenido excelentes resultados de aprendizaje significativo haciendo énfasis en los procesos en lugar de los contenidos, los cuales se han vuelto el centro del aprendizaje tradicional (Beltrán, 2010).

Así pues, existen aún aspectos importantes por cambiar, entre ellos: la práctica mecánica como método único y exclusivo de enseñanza y aprendizaje, ya que pese a los tantos escritos referidos al aprendizaje significativo, nuestros estudiantes continúan adquiriendo aprendizajes poco significativos. Esta es una razón que nos lleva a insistir en la comprensión y explicación de teorías de aprendizaje significativo (Rodríguez, 2011) que permitan desarrollar estrategias didácticas e innovadoras para que los alumnos aprehendan el verdadero significado de los conceptos que están estudiando. En esto radica la importancia de esta investigación, la cual nos facilitará el reconocimiento de los procesos que aplican los estudiantes sobre el concepto de funci para poder usar estas ideas como base en el diseño de estrategias de aprendizaje, dando continuidad al trabajo de otros investigadores como Janakievska, Stojanovska, Bogatinoska (2012); Aranzazu (2013); Espinoza (2017); Sychocki da Silva, Dos Reis Pinto (2018), cuyos estudios hicieron aportes para el desarrollo de estrategias didácticas con el uso de recursos que promueven un aprendizaje verdaderamente significativo de las funciones cuadráticas.

Al momento de enseñar matemáticas se deben considerar algunas variables que intervienen en todo proceso de aprendizaje, como el aspecto social, cognitivo y emocional (Gómez; Oviedo; Martínez, 2011), los cuales pueden influir directamente en el aprendizaje del estudiante. Sin embargo, una clase de matemática debe ser estructurada y guiada por el docente para que el alumno sea capaz de asimilarla de manera fluida y logre un aprendizaje significativo; para ello, es importante considerar la clase de matemática como un ambiente particular del estudiante, donde él mismo, con la ayuda y guía del profesor, está construyendo su conocimiento regido por ciertas directrices sociales e institucionales (Larios; Arellano; González, 2018), lo cual permite una fluidez natural en el aprendizaje.

En este artículo se analiza el proceso de aprendizaje aplicado por estudiantes para resolver problemas de matemáticas, específicamente el propuesto por Ausubel (1983) quien lo clasificó en dos tipos: aprendizaje mecánico y aprendizaje significativo, y en base a esta teoría desarrollar este trabajo. Para ello, se consideran las estrategias y técnicas que aplican los estudiantes cuando resuelven determinados problemas, así como el modo en que las emplean. 

1. Referentes teóricos

De acuerdo con España (2014), un proceso se define como una serie sistemática de fases que permiten el desarrollo de un fenómeno natural o de una operación artificial, entendiendo estas como etapas que un individuo realiza para organizar su conocimiento respecto a un tema particular, lo que involucra un proceso mental. Martínez (1992) define a este último como “procesos cognoscitivos, definidos a grandes rasgos como receptores y manipuladores de información” (p. 145), es decir, el sujeto recibe información sobre determinado tema, produciendo en él una serie de actividades mentales que le permiten adecuar esta información según su estructura cognitiva para obtener un resultado, entendiendo por estructura cognitiva el conjunto de ideas que una persona posee sobre un tema en particular y la forma como lo relaciona con otros conceptos (Ausubel, 1983). Esto se refiere a los conocimientos previos del individuo, definidos por Rayas (2004) como “aquellas concepciones que los estudiantes han adquirido sobre diferentes conocimientos, tanto los construidos a partir de experiencias externas a la enseñanza sistemática como los creados en los procesos educativos”.

a. El proceso mental en el aprendizaje

El aprendizaje de un individuo se basa en sus conocimientos previos, siendo estos el motor que permite impulsar los nuevos conceptos que está por aprender. Resumido por Ausubel (1983), “el factor más importante que influye en el aprendizaje es lo que el alumno ya sabe. Averígüese esto y enséñese consecuentemente” (p. 2). En este sentido, es importante diferenciar entre dos tipos de aprendizaje: mecánico y significativo, los cuales fueron presentados por primera vez hace varias décadas por Ausubel (1983), pero que siguen vigentes en nuestros sistemas educativos. Desde esta perspectiva, el aprendizaje significativo es un referente necesario para el diseño de los planes de estudio en un ambiente donde predomina la enseñanza para estimular un aprendizaje mecánico (Moreira, 2017).  

b. Aprendizaje significativo vs. aprendizaje mecánico

Trabajos recientes (Cuevas et al., 2015; Espinoza, 2017; Perdomo, 2016) muestran que desde hace algunos años se ha destacado la importancia que tiene que los estudiantes sean formados a partir de una metodología que permita en ellos un aprendizaje significativo, lo cual ha llevado a numerosas propuestas de estrategias de enseñanzas que involucran la innovación educativa a partir del uso de tecnologías, actividades lúdicas, contextualización de conceptos en la realidad, entre otros. Sin embargo, pese a todos estos esfuerzos por mejorar la educación, aún es común encontrar docentes que continúan aplicando métodos de enseñanza que incentivan el aprendizaje mecánico de los estudiantes (Castellanos, 2017), problema presente en todos los niveles de educación. A continuación, se exponen breves comentarios para aclarar la diferencia entre los dos tipos de aprendizaje.

Un aprendizaje significativo se logra cuando el individuo es capaz de relacionar de manera crítica y reflexiva el concepto que está por aprender con su conocimiento previo (Castellano et al., 2018). Por ello, los docentes deben enfocarse en los conocimientos previos que ya tienen los estudiantes, pues aquellos son la base que permite adquirir los nuevos conocimientos (Acosta, Andrade, 2013). Ausubel (1983) habla de una relación sustancial y no arbitraria, entendiendo por ello que las ideas se conectan entre sí con aspectos específicos y relevantes de la estructura cognoscitiva del estudiante, como imágenes, símbolos, conceptos o proposiciones. De esta manera, el aprendizaje significativo puede entenderse como la retención de nuevos conocimientos con significado que le permiten al alumno la posibilidad de aplicarlos en distintos contextos para buscar la solución de algún problema (Moreira, 2017). De acuerdo con esta teoría, para lograr que el estudiante adquiera un aprendizaje significativo de un tema en particular, debe considerarse con mayor importancia lo que ya sabe en lugar de lo que va a aprender, de manera que, para poder presentarse este tipo de aprendizaje, es indispensable que exista la disponibilidad de conocimientos previos en el estudiante (Masó, 2016).

El aprendizaje mecánico, por el contrario, se refiere a un aprendizaje memorístico, sin significado para el estudiante, basado meramente en grabar en la memoria imágenes o símbolos con el objetivo de responder a algún problema, sin comprender el sentido de este y las consecuencias intrínsecas de su solución (Moreira, 2017). En el aprendizaje mecánico no existe en el estudiante una actitud significativa de aprender (Rodríguez, 2011), es decir, el estudiante no muestra un interés en conocer de fondo los conceptos que va a aprender, solo se limita a memorizar respuestas correctas sin captar sus significados (Moreira, 2017), trayendo como consecuencia que una vez adquirido este aprendizaje tendrá dificultad para utilizarlo fuera del contexto en el que lo memorizó, porque solo se reproduce de la misma manera que fue aprendido (Díaz, 2002)

Asimismo, el aprendizaje mecánico, más allá de no ser significativo para el estudiante, puede tener consecuencias peores, generando una reacción negativa hacia la materia de enseñanza, especialmente en matemáticas (Moreira, 2017), lo cual puede ser una de las causas del bajo rendimiento académico en esta asignatura. A pesar de esto, nos encontramos en el aula algunos docentes que en sus clases se restringen a hacer de sus estudiantes simples memorizadores de conceptos, fórmulas, tablas, etc., incentivando un aprendizaje mecánico y memorístico que el alumno no podrá utilizar efectivamente en sus estudios posteriores (Beltrán, 2002).

A partir de lo anterior, es importante hacer dos aclaraciones: en primer lugar, debemos entender que en el aula el aprendizaje siempre debe traer como consecuencia un cambio significativo en el constructo mental del estudiante, permitiéndole una comprensión amplia para diferentes contextos. Esto significa que cuando un aprendizaje es mecánico, de fondo no ha sido un aprendizaje (Beltrán, 2002), ya que el hecho de memorizar o repetir alguna información solo para responder un test no implica que se haya logrado un aprendizaje significativo que permita aplicar los conceptos adquiridos fuera del contexto donde se adquirieron, es decir, no aprendió.

En segundo lugar, es importante dejar claro que no se pretende hacer pensar al lector que el aprendizaje mecánico es una forma errada de aprender y que no deba ser utilizado, puesto que, de hecho, en los primeros años de vida todos aprendemos de esta manera o bien cuando iniciamos una fase de un nuevo conjunto de conocimientos que no requiere de ideas previas relevantes (Ausubel, 1983). Sin embargo, lo que no se puede permitir es que durante los años de escolaridad los docentes continúen estimulando este único tipo de aprendizaje, pues a estos niveles los estudiantes ya están en la capacidad de desarrollar un pensamiento crítico, como para enseñarles a aprender, entendiendo que esto significa aprender a pensar (Beltrán, 2002), y para esto el docente debe desarrollar estrategias metodológicas apoyadas en actividades que estimulen un pensamiento crítico y analítico. 

c. Proceso de aprendizaje en matemáticas

Una de las causas del fracaso escolar puede ser las dificultades de aprendizaje en matemáticas (Fernández, 2013), ya que interrumpen de manera dramática su formación profesional, siendo la matemática una base para los procesos superiores de pensamiento (síntesis, análisis, evaluación, abstracción de conceptos complejos, etc.) (Ramírez, 2009). Pueden ser muchas las causas que produzcan la dificultad en esta área; por ejemplo, los estudiantes no parecen tener ningún interés en aprender (Skovsmose, 2018), ya que tienen otras prioridades y su nivel de madurez no les permite centrarse en su formación cognitiva. Además, el grado de dificultad propio de la matemática ha parecido ser una de las principales razones para su rechazo, aunque, Fernández-Gago, Carrillo, Conde (2018) asocian la idea de dificultad a la falta de conciencia que tienen los estudiantes respecto a las destrezas que necesitan para poder resolver los problemas que se les plantea, lo cual se relaciona directamente con falta de interés.

Finalmente, existe un problema intrínseco de la matemática que surge de los fundamentos que el estudiante debe afianzar a medida que avanza en sus estudios, ya que no los ubica en su memoria a largo plazo y por tanto no pueden utilizarlos para los siguientes niveles (Mota, Valles, 2015). Esto se relaciona directamente con el aprendizaje significativo de Ausubel (1983) que hace referencia a los conocimientos previos, solo que en matemáticas pareciera ser más notoria esta situación, considerando que para resolver un problema en esta área generalmente son necesarios los conocimientos previos que se relacionan con el problema para poder organizar los datos y dar una solución adecuada (Larios, Arellano, González, 2018).

Actualmente, pareciera que enseñar al estudiante los pasos y procedimientos que le permiten encontrar un resultado bastaría para enseñar matemática, o en un mejor contexto limitarse a enseñar los conceptos matemáticos para que de una manera ya predeterminada (mecánica) logren responder a determinado problema, pero hay que recordar que además de los conceptos, los problemas, algoritmos, notaciones, etc., también constituyen el conocimiento matemático (Vicenc, Godino, D’Amore, 2007). De esta manera, es importante considerar que debe existir una armonía entre los que señalan las directrices curriculares en cuanto a contenido y la construcción del conocimiento, minimizando la memorización de reglas y fórmulas (Sychocki da Silva, Dos Reis Pinto, 2018) e incentivando el aprendizaje a partir de la reflexión y el razonamiento.

A partir de lo anterior, se ha desarrollado esta investigación centrada en los procesos que aplican los estudiantes de bachillerato en la resolución de problemas matemáticos considerando que son tan importantes los procedimientos y métodos empleados como el resultado final (Larios, Arellano, González, 2018). Si bien es relevante que la respuesta del estudiante sea correcta, debe importar tanto o más los procesos cognitivos que relacionan la comprensión y el significado de los conceptos involucrados en el problema. Vicenc, Godino, D’Amore (2007) aseguran que hablar de significado y comprensión implica hablar de conocimiento matemático, considerando las producciones cognitivas y sus relaciones con el entorno. Por ello, la importancia de enseñar a los estudiantes a realizar conjeturas, explorar y argumentar, desarrollando conocimiento mediante un proceso significativo mediante el énfasis en la comprensión del proceso y del resultado (Larios, Arellano, González, 2018). 

d. Estrategias y técnicas de aprendizaje en matemática

Si un estudiante adquiere un aprendizaje significativo, indica que durante el proceso ha reflexionado sobre los pasos que sigue para poder dar respuesta a su problema (Mota, Valles, 2015), es decir, ha generado una estrategia de resolución del problema y en función de ella podrá elegir la técnica que más se adecúe al proceso. Para esta investigación, es importante entender la diferencia entre estrategia y técnica.

La enciclopedia de la Real Academia Española (España, 2014) define la estrategia como una actividad regulable que conlleva una serie de pautas que permite tomar decisiones acertadas en determinados momentos. En otras palabras, implica un proceso sistemático y planificado en función de un objetivo particular que lleva a un fin particular. Específicamente, en el proceso de aprendizaje hablamos de estrategias de aprendizaje como una serie de actividades que se planifican de acuerdo con las necesidades del alumno (Molina, Lovera, 2008). Para Camarero, Martín del Buey, Herrero (2000), las estrategias de aprendizaje pueden mostrar sus actividades en cuatro fases: en principio, adquisición, codificación y recuperación de la información, y finalmente apoyo a su procesamiento fundamentado en la autodeterminación del individuo.

De acuerdo con esto, se puede apreciar que una estrategia, desde la perspectiva del estudiante, implica un proceso reflexivo de la información recibida que le permite organizarla y juzgar, según su criterio, el mejor camino a seguir para lograr su objetivo; las estrategias de aprendizaje implican la toma de decisiones, por lo que siempre es una reflexión consciente e intencional donde se pretende que el alumno realice los ajustes para el logro del objetivo 
o dirigirlos a la obtención de metas de aprendizaje (Herrera, 2009). Así pues, las estrategias de aprendizaje son, en conjunto con los contenidos, objetivos y la evaluación, componentes fundamentales del proceso de aprendizaje (Molina, Lovera, 2008), de allí la importancia de ayudar a los estudiantes a desarrollar habilidades que les permitan aplicar estrategias durante la resolución de un problema matemático.

Por otro lado, cuando hablamos de técnicas nos referimos a un conjunto organizado de pasos, que fueron previamente diseñados para conseguir algún propósito. Salazar (2004) las define como acciones propias o muy particulares que desarrollan los estudiantes cuando aprenden: repetición mediante la lectura, subrayar palabras o ideas, jerarquizar conceptos, hacer preguntas, deducir, inducir, inferir, copiar, entre otras, que pueden ser manejadas de forma mecánica. En matemática y física una técnica puede limitarse a aplicación de meras fórmulas o elaboración de gráficos de manera mecánica. 

En ese sentido, podemos notar que una estrategia lleva consecuentemente a una técnica; es decir, al momento de diseñar una estrategia se desarrollan acciones a seguir conscientes e intencionales (Salazar, 2004), reflexionamos sobre ellas y luego decidimos qué técnica es más conveniente aplicar a determinada situación. Nótese que, igualmente, es posible resolver un problema simplemente aplicando una técnica adecuada, sin necesidad de reflexionar sobre este; sin embargo, esto sería evidencia de un aprendizaje mecánico, donde el estudiante no necesariamente tiene un entendimiento claro de los conceptos involucrados en el desarrollo de su trabajo, lo que significa que no hay un aprendizaje significativo.

Esta investigación, trata específicamente las funciones cuadráticas, como eje para diversos temas en matemáticas; para esto se ha seleccionado un instrumento que se fundamenta en problemas de contexto cuyas soluciones pueden conseguirse haciendo un análisis funcional, específicamente con una función cuadrática. Pino-Fan, Parra-Urrea, Castro-Gordillo (2019) aseguran que algunos estudios sobre propuestas para la enseñanza de la función establecen la necesidad de analizarla a partir de situaciones contextualizadas, motivo por el cual hemos elegido abordar esta investigación a partir de este tipo de situaciones.

Para estudiar los procesos que desarrollan los estudiantes cuando se encuentran con un problema de matemáticas relacionado con las funciones cuadráticas, hemos utilizado como fundamento teórico el tipo de aprendizaje que atienden los estudiantes cuando están en clases de matemática, tomando como dimensiones de la variable de investigación el aprendizaje significativo y aprendizaje mecánico.

La figura 1 ilustra un resumen de la secuencia que puede seguir el proceso de aprendizaje de acuerdo con lo descrito anteriormente.

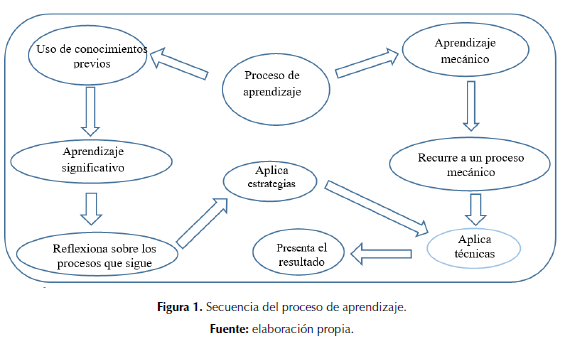
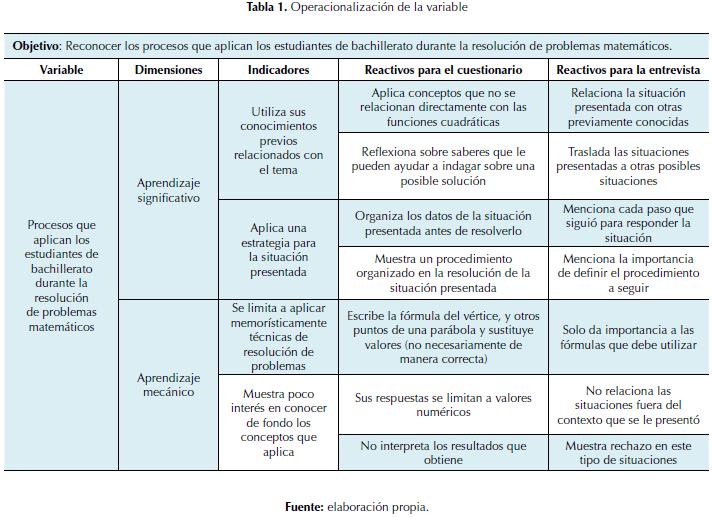
La tabla 1 detalla la operacionalización de la variable en función de las dos dimisiones consideradas con sus respectivos indicadores y reactivos. 

2. Metodología de investigación

La metodología de esta investigación es de tipo descriptivo-cuantitativo. A continuación, se describe con el fin de analizar los datos que se recogieron y que estos a su vez permitan responder nuestra pregunta de investigación: ¿Cuáles son los procesos que aplican los estudiantes de bachillerato durante la resolución de problemas matemáticos?, usando como caso de estudio la función cuadrática. 

a. Diseño y tipo de investigación

El diseño de una investigación se refiere al plan o estrategia que se adopta para obtener la información deseada (Hernández, Fernández, Baptista, 2010). Esta investigación estuvo enmarcada en el diseño cuantitativo no experimental, ya que el estudio se realizó sobre un grupo de estudiantes de primero de bachillerato que recibieron las clases regulares de funciones correspondientes a su curso y en las que no se intervino, para evitar modificar los procesos que aplicaban durante la resolución de problemas relacionados con las funciones cuadráticas. Para Hernández, Fernández, Baptista (2010), la investigación no experimental se refiere a realizar observaciones de fenómenos tal cual como ocurre en su contexto de origen para ser analizados. De igual manera, dentro del diseño no experimental, la investigación se enmarcó en el tipo transeccional descriptivo, con el propósito de indagar la incidencia de los procesos mentales que siguen los estudiantes de primero de bachillerato en el tema en cuestión, en un tiempo único (Hernández, Fernández, Baptista, 2010), por lo que los investigadores se limitaron a registrar los datos inéditos producidos por los estudiantes en un momento específico. 

b. Población y muestra

En este estudio se consideró una población conformada por dos cursos del primer año de bachillerato de estudiantes con edades comprendidas entre 15 y 17 años, de una unidad educativa privada, ubicada al norte de Quito (Ecuador). Para seleccionar la muestra se aplicó una técnica de muestreo no probabilística, ya que la finalidad no fue generalizar en términos de probabilidad sino responder a nuestra pregunta de investigación sobre un grupo específico de estudiantes, y se consideró la riqueza, profundidad y calidad de la información obtenida, más que la cantidad o estandarización de los resultados (Hernández, Fernández, Baptista, 2014). Los autores señalan que este tipo de muestra es un subgrupo de la población en la que la elección de los elementos no depende de la probabilidad o fórmulas, sino de las características de la investigación o de quien la hace. En este caso, la selección fue de 38 estudiantes de manera intencionada, y se tuvieron en cuenta factores como disposición para colaborar en la investigación, constancia en las clases y actitud de trabajo; esto con el propósito de evadir resultados que pudieran ser producto motivaciones 
o intereses propios del estudiante. 

c. Técnicas e instrumentos de recolección de información

Este estudio recurrió, para la obtención de la información, a la implementación de un cuestionario seguido de una entrevista semiestructurada. De manera que se utilizaron dos instrumentos para recabar la información: i) el cuestionario, donde se presentaron cuatro situaciones que involucraban funciones cuadráticas, y el cual se aplicó durante un tiempo de 90 minutos, tiempo suficiente para que el estudiante pudiera escribir con calma cualquier método que se le ocurriera de manera detallada; y ii) la entrevista semiestructurada, cuyo fin fue obtener la mayor cantidad de información sobre todos los procesos empleados por los estudiantes a la hora de resolver los problemas. Este se aplicó una vez que los cuestionarios fueron revisados por los investigadores, lo que facilitó a los estudiantes expresar verbalmente las estrategias o técnicas de resolución de problemas que emplearon durante el desarrollo de las preguntas propuestas.

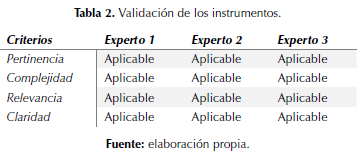
Dichos instrumentos fueron sometidos a la revisión de tres expertos en enseñanza de la matemática, quienes validaron la pertinencia, complejidad, relevancia y claridad del instrumento coincidiendo en que aquellos eran aplicables para el estudio (tabla 2). 

Primer instrumento: el cuestionario

Este instrumento constó de cuatro situaciones problemas relacionadas todas con el concepto de funciones cuadráticas. Cada una pretendió medir el proceso que siguió el estudiante para dar su respuesta al problema. Este cuestionario fue seleccionado por los investigadores, ya que permitió colocar en situación a los estudiantes; así ellos estaban habilitados para recurrir a sus conocimientos previos, evidenciar la manera de raciocinio y poner de manifiesto los procesos mentales que este tipo de situaciones contextualizadas generan en ellos. Esto fue coherente con los postulados de Pino-Fan, Parra-Urrea, Castro-Gordillo (2019).

Primera situación (Huircan, Carmona, 2013 p. 39):

1) Se lanza una bola verticalmente, alcanzando una altura en cada instante t la cual está dada por la funci: h (t) = -4t2 + 68t + 160, donde h ( t ) se mide en cm y el tiempo t en segundos.

a)Escriba los valores h(t) para cada valor del tiempo. 

b) Grafique la función h(t ). 

c)¿Cuánto tiempo tarda la bola en alcanzar su altura máxima? 

d) ¿Cuál es la altura cuando la velocidad final es nula? 

e) ¿Cuál es el tiempo de vuelo de la bola?

Segunda situación (Huircan, Carmona, 2013 p. 41)

Se debe construir un corral rectangular utilizando como uno de sus muros una roca para economizar malla de cerco. Determine las dimensiones del área máxima del corral si se dispone de 18 metros de malla para cercar.

Tercera situación (Huircan, Carmona, 2013 p. 40)

El tiempo (en minutos) de reacción, f(x), de una plaga de insectos al contacto con un plaguicida está descrita por la función: f ( x ) = x ( 9 - x ), donde x es la cantidad de insecticida en mg/l (0<x<9, se debe usar menos de 9 mg/l de insecticida debido a los costos)

a) ¿Con cuánta cantidad de plaguicida se obtiene el tiempo óptimo para la reacción?

b) ¿Cuál es el tiempo óptimo para la reacción?

Cuarta situación (Huircan, Carmona, 2013 p. 41)

En momentos de crisis econónica, una compañía no desea tener pérdidas, si x son las unidades de productos vendidos, la utilidad que se obtiene está dada por la función: U(x)= -x2+ 120x + 1.300. Determinar para qué valores de x, no hay pérdidas ni utilidades.

Con este instrumento se pretendió medir en los estudiantes si al momento de enfrentarse con un problema de aplicación de las funciones cuadráticas estos eran capaces de reflexionar sobre los procedimientos que seguían para diseñar una estrategia adecuada y dar respuesta al problema, o simplemente se limitaban a aplicar procesos mecánicos por medio de una técnica específica durante la resolución.

Segundo instrumento: la entrevista

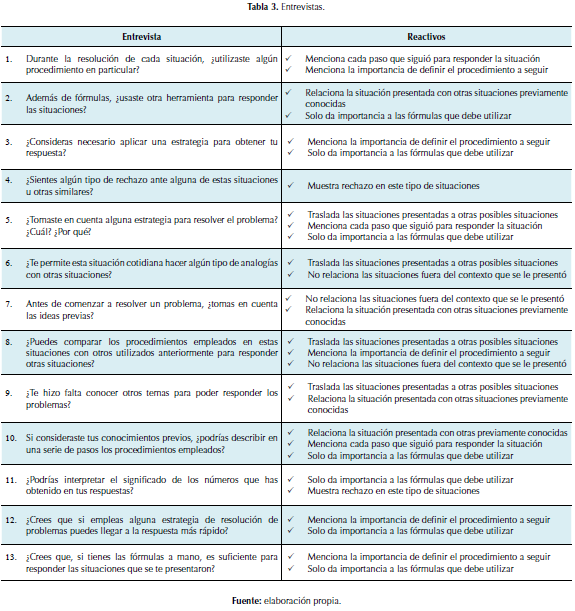
El segundo instrumento aplicado a cada estudiante de la muestra fue una entrevista semiestructurada, preguntas donde el entrevistador tiene la posibilidad de generar nuevas interrogantes que le ayuden a precisar conceptos u obtener mayor información (Hernández, Fernández, Baptista, 2014), la misma fue elaborada a partir de trece preguntas, que se fundamentaban básicamente en extraer información adicional a la que se reflejó por escrito en el cuestionario. Es decir, se buscó directamente del estudiante cualquier otra información que no hubiera suministrado en el cuestionario por causas como: tiempo, nervios, falta de claridad en el momento, falta de conocimiento para escribir su respuesta o cualquier otra. Por otra parte, los reactivos de la entrevista fueron elaborados a partir de los elementos teóricos expuestos anteriormente; con lo que se pretendió recabar información pertinente para la investigación. En la tabla 3 pueden apreciarse las preguntas realizadas en la entrevista junto al reactivo que se consideró para cada una de ellas. 

d. Fases de la investigación

La investigación se llevó a cabo en dos fases: selección y recolección de información:

Selección: estuvo comprendida entre los primeros cuatro meses del año escolar, durante el cual se seleccionó a un grupo de estudiantes del primer año de bachillerato quienes estaban estudiando el tema de las funciones, durante esta etapa de la investigación el docente se limitó a impartir sus clases utilizando sus métodos tradicionales de enseñanza y siguiendo la secuencia regular de la unidad que se corresponde al tema en cuestión.

Recolección de información: consistió en la recolección de información a través de los instrumentos elaborados. Culminada la fase de selección se aplicó el cuestionario a la muestra tomada, para ello se les pidió a los estudiantes que se sintieran en libertad de responder con cualquier método que consideraran pertinente y que, en la medida de lo posible, escribieran todo lo que hacían. Una vez que el cuestionario fue revisado por los investigadores, se les entrevistó uno por uno con ayuda del instrumento 2, para que pudieran explicar con sus propias palabras lo que en el cuestionario no reflejaron.

e. Recolección de información

Aquí se consideraron dos dimensiones: aprendizaje significativo y aprendizaje mecánico. Para ello, se utilizaron tablas de frecuencias que permitieron organizar la información contrastando las situaciones presentadas en el cuestionario con los indicadores mencionados en la tabla 1 de acuerdo con sus respectivos reactivos. Para rellenar las tablas se revisaron cada uno de los 38 cuestionarios, situación por situación, para poder contabilizar la concurrencia de cada reactivo. Luego, para complementar los datos recogidos hasta el momento, se escucharon las entrevistas de cada estudiante en atención a los reactivos correspondientes. Las tablas 4, 5, 6 y 7 que se presentan en el análisis de los resultados muestran la frecuencia absoluta y porcentual de los reactivos que se corresponden con cada indicador de cada dimensión. 

3. Análisis de los resultados

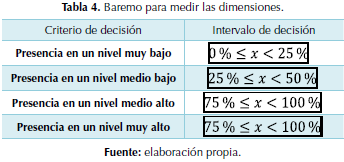
El análisis se realizó mediante la estadística descriptiva, y para categorizar los resultados se definió un baremo. Los intervalos de decisión se consideraron según la puntuación obtenida de uno (1) a cuatro (4)puntos en cada reactivo del cuestionario; donde cada punto representa un intervalo como puede apreciarse en la tabla 4. Mediante la conformación de las tablas de frecuencias se cuantificaron las respuestas a los reactivos y los porcentajes relacionados con estas, para posteriormente comparar los datos con el baremo presentado en dicha tabla, cuyo fin es categorizar la información recabada.

a. Uso de los conocimientos previos

La tabla 5 muestra un resumen de los datos recabados para el primer indicador de la dimensión 
aprendizaje significativo.

En la tabla 5 podemos observar los resultados que se obtuvieron de la dimensión aprendizaje significativo con respecto al indicador “utiliza sus conocimientos previos relacionados con el tema”. Este fue medido a través de la cuantificación de cuatro reactivos que pueden detallarse en la tabla 5. Se observa que el reactivo “aplica conceptos que no se relacionan directamente con las funciones cuadráticas” está presente en un 32 % de las personas encuestadas, lo que se puede valorar con una presencia en un nivel medio bajo según el baremo. En referencia al reactivo “reflexiona sobre saberes que le pueden ayudar indagar sobre una posible solución”; presenta un porcentaje del 50% que es cuantificado con una presencia en un nivel medio alto entre los estudiantes objeto de estudio. En relación con el reactivo “relaciona la situación presentada con otras situaciones previamente conocidas”, está valorado con una presencia muy baja apenas alcanzando un porcentaje del 13 %. Ya para finalizar el conjunto de reactivos de este indicador, tenemos que el reactivo “traslada las situaciones presentadas a otras posibles situaciones” está cuantificado con un 26% que se valora según el baremo con una presencia entre los encuestados como medio bajo. 

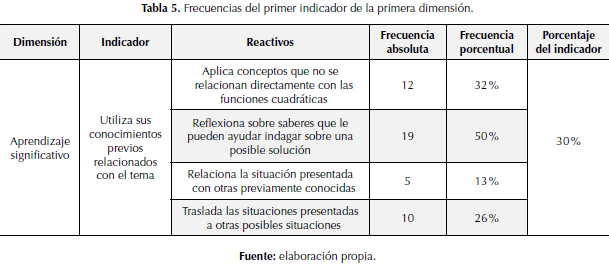
Luego de cuantificar y valorar los reactivos correspondientes a este indicador se pudo obtener una media porcentual entre los reactivos que representaron el indicador, el cual, de acuerdo con el baremo, está valorado en la categoría de presencia media baja en los estudiantes, y alcanzó un porcentaje del 30% de la muestra. De acuerdo con estos resultados, es posible afirmar que el indicador “utiliza sus conocimientos previos relacionados con el tema” es una carencia que presentan los estudiantes de bachillerato.

En concordancia con esta idea, podemos mencionar la respuesta a la pregunta “Antes de comenzar a resolver un problema, ¿tomas en cuenta las ideas previas?”, que se le realizó durante la encuesta a uno de los estudiantes y cuya respuesta fue: “¡No! No, no, solo comencé leyendo y aplicando las fórmulas”. Esta fue muy común en los estudiantes mientras eran entrevistados, lo cual evidencia que, según ellos, no es necesario recurrir a sus conocimientos previos para dar respuesta a una situación, en contraposición a lo que señalan Acosta, Andrade (2013), quienes afirman que las ideas previas son la base para promover el conocimiento. 

b. Aplicación de estrategias

En la tabla 6 se muestra el resumen de los datos recabados para el segundo indicador de la dimensión aprendizaje significativo.

El segundo indicador considerado para la primera dimensión aprendizaje significativo fue “aplicación de estrategias para resolver la situación presentada”. Este fue analizado por medio de cuatro reactivos: “organiza los datos de la situación presentada antes de resolverlo”, categorizado con una frecuencia porcentual de 79%, valorado como una presencia entre la población muy alta según el baremo. Como segundo reactivo de este indicador está “muestra un procedimiento organizado en la resolución de la situación presentada”, estimado con una frecuencia de 42%, es decir, este reactivo está presente entre los estudiantes en el intervalo medio bajo. Seguidamente, se tiene el reactivo “menciona cada paso que siguió para responder la situación”; alcanzó un de 16% de frecuencia entre la población objeto de estudio, valorado como una presencia muy baja. Por último, está el reactivo “menciona la importancia de definir el procedimiento a seguir”, el cual ha sido cuantificado con 21 %, categorizado como una presencia muy baja. 

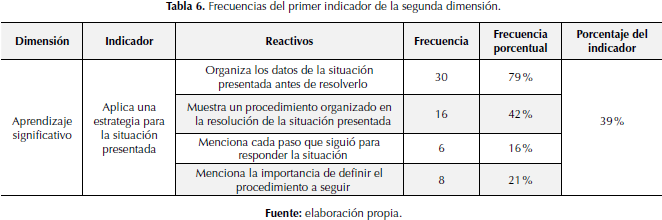
En consecuencia, en la tabla 5 se evidencia que la media porcentual de este indicador está valorada con una frecuencia porcentual de 39% que según el baremo está en la categoría de presencia media baja. Finalmente, observando los dos indicadores que permiten medir la dimensión aprendizaje significativo, según los resultados mostrados en las tablas 4 y 5, podemos ver que, en ambos hay presencia en un nivel medio bajo. 

Estos resultados son contrarios a las ideas manifestadas por Molina, Lovera (2008); Camarero, Martín del Buey, Herrero (2000), quienes afirman que las estrategias de aprendizaje cuando son asimiladas por los estudiantes y hay un evidente dominio, permiten que el estudiante desarrolle sus saberes y a su vez pueda realizar nuevos ajustes que permiten la adaptación a otros contextos, lo que conlleva de manera intrínseca a desarrollar procesos metacognitivos de regulación de cómo se aprende. Sin embargo, en este estudio se evidencia que los jóvenes que respondieron ante las situaciones propuestas para recabar información, no se han apropiado de estrategias y técnicas que permitan desarrollar soluciones a las situaciones propuestas en esta investigación. A pesar de que en un porcentaje alto (79%) son capaces de organizar los datos de la situación antes de resolverlo, el resto de los indicadores nos muestran que el estudiante no termina de establecer una estrategia bien definida para su propósito, y aun cuando logra encontrar la respuesta no es capaz de darle un significado a esta. 

c. Aplicación memorística de técnicas de resolución de problemas

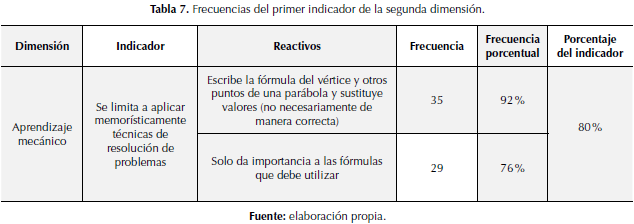
La tabla 7 muestra un resumen de los datos recabados para el primer indicador de la dimensión aprendizaje mecánico.

Para analizar el aprendizaje mecánico se utilizaron dos indicadores, en la tabla 6 se muestra el primero de ellos: se limita a aplicar memorísticamente técnicas de resolución de problemas; que ha sido cuantificado a través de dos reactivos; por un lado, “escribe la fórmula del vértice y otros puntos de una parábola y sustituye valores”, que presenta una frecuencia del 92%, lo que se puede traducir que tiene una presencia muy alta entre las personas encuestadas. Por otra parte, el siguiente reactivo de este indicador: “Solo da importancia a las fórmulas que debe utilizar”, está cuantificado con la frecuencia del 76%, es decir que está presente en la categoría de muy alto.

Según los resultados obtenidos con los reactivos, se puede observar que la media porcentual del indicador de la tabla 6, alcanza un porcentaje del 80%, lo que es valorado con una presencia muy alta. Podemos reforzar estas ideas con resultados de la entrevista hecha a un estudiante, quien al preguntarle en referencia a la primera situación: “Durante la resolución de cada situación, ¿utilizaste algún procedimiento en particular? Explica”, este respondió: “¡No! Solo utilicé la fórmula para calcular los segundos de la pelota”. Este tipo de respuesta fue muy común en las entrevistas, lo cual nos muestra que el estudiante no ha reflexionado sobre los conceptos que pudiera utilizar y solo se está basando en aplicar fórmulas sin sentido para resolver el problema, consecuencia evidente de un aprendizaje mecánico. 

d. Interés de conocer de fondo los conceptos que aplica

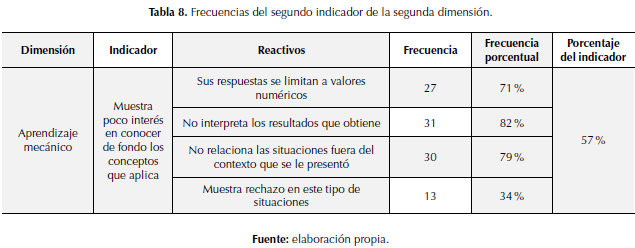
Finalmente, se muestra un resumen de los datos recabados para el segundo indicador de la dimensión aprendizaje mecánico.

El indicador fue analizado por medio de cuatro reactivos: “sus respuestas se limitan a valores numéricos”, presentando una frecuencia del 71%, categorizado con una presencia media alta según el baremo. Por otra parte, el siguiente reactivo de este indicador: “No interpreta los resultados que obtiene”, está cuantificado con la frecuencia más alta de este estudio con un 82%, es decir que está presente en la categoría de muy alto. También podemos observar el reactivo “no relaciona las situaciones fuera del contexto que se le presentó” que se encuentra valorado por la población estudiada con un 79% de presencia muy alta. Finalmente, para el estudio y análisis del indicador en la tabla 7 está el reactivo “muestra rechazo en este tipo de situaciones”; con frecuencia del 34%, categorizada con una presencia media baja.

En este sentido, en este segundo indicador: “muestra poco interés en conocer de fondo los conceptos que aplica”, los cuatro reactivos que lo cuantificaron permiten valorar la media porcentual, categorizado con el 57 % de presencia, lo que lo ubica con una presencia media alta de acuerdo con al baremo que estamos utilizando.

En consecuencia, estos respectivos análisis evidencian que el aprendizaje mecánico está presente en un alto porcentaje, siento esto coherente con las ideas y planteamientos de Rodríguez (2011), Moreira (2017), Díaz (2002), con respecto al aprendizaje mecánico, pues se refiere a un aprendizaje memorístico, carente significado para el estudiante, basado meramente en grabar en la memoria imágenes, pasos o símbolos con el objetivo de responder a algún problema, sin comprender su sentido y las consecuencias intrínsecas de su solución. Es decir, el estudiante no muestra un interés en conocer de fondo los saberes que va a aprender y mucho menos como asociarlos para dar respuesta a situaciones de otros contextos; sin embargo, sí hace que el alumno desarrolle pasos memorizados que pueden dar respuestas medianamente correctas.

En coherencia con estas ideas, dentro de las evidencias logradas a través del trabajo de los jóvenes, podemos observar la figura 2, la cual muestra el desarrollo que realiza un estudiante cuando trata de resolver la cuarta situación. 

En la figura 2 se observa que el estudiante aplicó algunos algoritmos, que le permitieron obtener una respuesta, es decir, el desarrollo de la situación, encontrando los ceros de la función mediante una técnica de factoreo, y así consiguió dos números (uno positivo y otro negativo); optó por el positivo, y escribió su respuesta en función de eso, pero sin significado alguno. Cuando se entrevistó al estudiante y se le hizo la pregunta: “¿Te hizo falta conocer otros temas para poder responder los problemas?”, este respondió: “¡Ver qué tipo de ecuación tengo, el resultado fue un trinomio cuadrado perfecto, se hace el ejercicio de trinomio cuadrado perfecto y se llega a la solución de x que es 130!”.

Esta situación es recurrente, la muestra de respuestas a través de un número, que muchas veces carece de significado pues la mayoría de los estudiantes no realizan ni reflexionan sobre la estrategia que los lleven a emitir una respuesta que dé un mayor valor al número conseguido.

Finalmente, los indicadores de la dimensión aprendizaje mecánico muestran una presencia bastante alta de un aprendizaje mecánico en los estudiantes seleccionados como muestra de estudio. 

4. Consideraciones y recomendaciones finales

Como resultado de esta investigación, se pueden mencionar algunos aspectos importantes que pueden responder nuestra pregunta de investigación: ¿Cuáles son los procesos que aplican los estudiantes de bachillerato durante la resolución de problemas matemáticos?

Los conocimientos previos fueron estrechamente utilizados por los estudiantes de la muestra, al responder las situaciones que se presentaron, aunque fueron concepciones que debieron adquirir a partir de otras experiencias académicas o no, y que, de acuerdo con la teoría estudiada, aquellos podrían haberles ayudado a ser más efectivos al momento de responder cada pregunta. Basados en esta observación, merece la pena notar la importancia que tiene para el desarrollo cognitivo del estudiante que el docente incentive sus ideas previas a través de estrategias de enseñanza/aprendizaje en el aula de clases.

Pocos estudiantes lograron adquirir un aprendizaje significativo en el estudio de las funciones cuadráticas, en su mayoría no fueron capaces de establecer una estrategia adecuada y efectiva para responder las situaciones presentadas, aunque un alto porcentaje de ellos logró organizar los datos presentes en las situaciones, pero pocos llegaron a ejecutar con efectividad el proceso a seguir para resolver los problemas.

El aprendizaje mecánico ha sido el proceso mayoritariamente presente en la muestra de estudio, lo que indica que los estudiantes prefieren en su mayoría limitarse a realizar cuentas sustituyendo valores numéricos en fórmulas y cuyos resultados no presentan significado alguno para ellos, lo cual afirma la postura de Moreira (2017) cuando asegura que en nuestros sistemas educativos predomina el aprendizaje mecánico y no el significativo.

En conclusión, los estudiantes siguen un proceso mecánico y memorístico para responder problemas de matemáticas, limitándose a aplicar técnicas basadas en su mayoría en fórmulas que no tienen sentido alguno más allá de lo numérico. Sin embargo, es importante mencionar que, en muchos casos, son capaces de organizar los datos de una situación determinada, pero no terminan de realizar un procedimiento adecuado que les permita obtener una respuesta correcta.

Para concluir, se espera que esta investigación sirva como fundamento teórico para diseñar experiencias académicas que estimulen un aprendizaje significativo, considerando lo difícil que puede ser diseñarlas si no se parte de los intereses y necesidades de los estudiantes (Arias-Rueda, Castro, Vega, 2017). 

Referencias bibliográficas

ACOSTA, S.; ANDRADE, A. Estrategias de enseñanza para promover el aprendizaje significativo de la biología en la Escuela de Educación, Universidad del Zulia. Revista Multiciencias, Punto Fijo, Venezuela, v. 14, n. 1, pp. 67–73. 2013. Disponible en: http://www.redalyc.org/pdf/904/90430816010.pdf

ARANZAZU, C. M. Secuencia didáctica para la enseñanza de la función cuadrática. Universidad Nacional de Colombia Sede Medellín. Medellín. 2013. Disponible en: <http://www.bdigital.unal.edu.co/11788/1/71644693.2013.pdf>. Visitado el 25 de febrero de 2019.

ARIAS, F. El proyecto de investigación. Introducción a la metodología científica. 6a. ed. Editorial Episteme. Caracas-Venezuela. 2012.

ARIAS-RUEDA, M. J., CASTRO, M.; VEGA, Y. Necesidades de aprendizaje en la formación de ingenieros. Un aporte a las experiencias integradoras entre Física e Inglés. Omnia, Maracaibo, Venezuela, n. 1, pp. 117–134. 2017.

AUSUBEL, D. Teoría del aprendizaje significativo. 1983. Disponible en <https://www.academia.edu/10435788/TEORÍA_TEORIA_DEL_APRENDIZAJE_SIGNIFICATIVO>. Visitado el 23 de enero de 2019.

BELTRÁN, J. (ed.). Procesos, estrategias y técnicas de aprendizaje. Síntesis. Madrid: España. 2002. pp. 1–38.

CAMARERO, F.; MARTÍN DEL BUEY, F.; HERRERO, J. Estilos y estrategias de aprendizaje en estudiantes universitarios. Psicothema, Asturias, v. 12, n. 4, pp. 615–622. 2000.

CASTELLANO G., J. M. et al. Un caso de estudio sobre conocimiento previo en tres universidades ecuatorianas: UC , UDA y UNAE. Estudios Pedagicos, Valdivia, Chile, v. 44, n. 1, pp. 377–402. 2018. https://doi.org/10.4067/S0718-07052018000100377

CASTELLANOS, A. J. Prácticas de laboratorio para promover el aprendizaje significativo del material y seguridad en el laboratorio, características de metales y no metales y formación de compuestos inorgánicos. Revista Criterios, Nariño, Colombia, v. 24, n. 1, pp. 235–262. 2017.

CUEVAS, R. E. et al. Corrientes teóricas sobre aprendizaje combinado en la educación. Revista Iberoamericana de Ciencias, Texas, Estados Unidos de América. 2015. Disponible en: <http://reibci.org/publicados/2015/enero/0800101.pdf>. Visitado el 25 de febrero de 2019.

DÍAZ A., F. Didáctica y currículo: Un enfoque constructivista. 1a. ed. Ediciones de la Universidad de Castilla-La Mancha. Cuenca. 2002. 

DÍAZ, C. et al. Dificultades de aprendizaje en las matemáticas, prevención y actuación. In GARCÍA, J. N. (coord.). Prevención en dificultades del desarrollo y del aprendizaje. Pirámide. Madrid: España. pp. 235–250. Disponible en <https:// www.researchgate.net/publication/261703968_Dificultades_de_aprendizaje_en_las_matematicas_prevencion_y_actuacion>. Visitado el 20 de febrero de 2019.

ESPAÑA. Real Academia Española. Diccionario de la lengua española. 23a. ed. Madrid. 2014. Disponible en <http://www.rae.es/diccionario-de-la-lengua-espanola/la-23a-edicion-2014>. Visitado el 20 de febrero de 2019.

ESPINOZA, J. Los recursos didácticos y el aprendizaje significativo. Espirales. Revista Multidisciplinaria de Investigación científica, Ecuador, v. 1, n. 2, pp. 33–38. 2017. Disponible en <http://www.revistaespirales.com/index.php/es/article/ view/4/3>. Visitado el 20 de febrero de 2019.

FERNÁNDEZ, C. Principales dificultades en el aprendizaje de las Matemáticas. Pautas para maestros de Educaci Primaria. Universidad Internacional de La Rioja. 2013. Disponible en: <https://reunir.unir.net/bitstream/hand-le/123456789/1588/2013_02_04_TFM_ESTUDIO_DEL_TRABAJO.pdf?sequence=1>. Visitado el 20 de enero de 2019

FERNÁNDEZ-GAGO, J.; CARRILLO, J.; CONDE, S.M. Un estudio de caso para analizar cómo ayudan los profesores en resolución de problemas matemáticos. Educación Matemática, México, v. 30, n. 3, pp. 247–276. 2018. https:// doi.org/10.24844/EM3003.10.

GOMÉZ, D.; OVIEDO, R.; MARTÍNEZ, E. Factores que influyen en el rendimiento académico del estudiante universitario. Tecnociencia Chihuahua, Chihuahua-México, v. 5, n. 2, pp. 90–97. 2011.

HERNÁNDEZ, R.; FERNÁNDEZ, C.; BAPTISTA, M.P. Metodología de la investigación. 5a. ed. McGraw-Hill Educación. México. 2010. <https://www.esup.edu.pe/descargas/dep_investigacion/Metodologia%20de%20la%20investigaci%C3%B3n%205ta%20Edici%C3%B3n.pdf> Visitado el 20 de febrero de 2019.

HERNÁNDEZ, R., FERNÁNDEZ, C.; BAPTISTA, M.P. Metodología de la investigaci. 6a. ed. Mc-Graw-Hill Educación. México. 2014.

HERRERA, A. Las estrategias de aprendizaje. Innovaci y Experiencias Educativas, Granada-España, n. 16, pp. 1–14. 2009. Disponible en: <http://prepajocotepec.sems.udg.mx/sites/default/files/estrategias_herrera_capita_0.pdf>. Visitado el 20 de febrero de 2019.

HUIRCAN, M.; CARMONA, K. Guía de Aprendizaje No 2. Las funciones cuadráticas: una herramienta de modelación. 1a. ed. Ministerio de Educación de Chile, RR Donnelley. Santiago de Chile. 2013.

JANAKIEVSKA, B.; STOJANOVSKA, L.; BOGATINOSKA, D. Enhanced study of quadratic functions with geogebra and preparation for calculus. In 8TH INTERNATIONAL SYMPOSIUM ON GEOMETRIC FUNCTION THEORY AND APPLICATIONS. Ohrid: Macedonia. 2012.

LARIOS, V.; ARELLANO, C.; GONZÁLEZ, N. Analysis of High School Students’ Arguments when Solving Geometry Problems. REDIMAT, Journal of Research in Mathematics Education, Bar-celona-España, v. 7, n. 3, pp. 280–310. 2018. https://doi.org/10.4471/redimat.2018.2343

MARTÍNEZ, P. Procesos mentales y cognitivismo. Revista de Filosofía, v. 5, n. 7, pp. 143–159. 1992. Disponible en <https://revistas.ucm.es/index.php/RESF/article/viewFile/RESF9292120143A/11832>. Visitado el 20 de diciembre de 2018.

MASÓ, Y. (2016). Estrategias de enseñanza de la propiedad intelectual en la enseñanza superior. KOINONIA. Revista Arbitrada Interdisciplinaria de Ciencias de la Educación, Turismo, Ciencias Sociales y Económica, Ciencias del Agro y Mar y Ciencias Exactas y Aplicadas, Santa Ana de Coro, Venezuela, v. 1, n. 2, pp. 74–102. Disponible en: <https://www.researchgate.net/publication/327755988_ESTRATEGIAS_DE_ENSENANZA_DE_LA_PROPIEDAD_INTELECTUAL_EN_LA_ENSENANZA_SUPERIOR>. Visitado el 20 de enero de 2019.

MOLINA, D.; LOVERA, Z. Significado que le otorgan los docentes a las estrategias de evaluación de los aprendizajes. Ciências & Cognição, Río de Janeiro, Brasil, v. 13, pp. 82–93. 2008. Disponible en: <http://www.cienciasecognicao.org/pdf/v13/m318207.pdf>. Visitado el 20 de diciembre de 2018.

MOREIRA, M. A. Aprendizaje significativo como un referente para la organización de la enseñanza. Archivos de Ciencias de la Educación, Buenos Aires-Argentina, v. 11, n. 12, pp. 0–16. 2017. https://doi.org/10.24215/23468866e029

MOTA, D.; VALLES, R. . Papel de los conocimientos previos en el aprendizaje de la matemática universitaria. Acta Scientiarum Education, Maringá-Brasil, v. 37, n. 1, pp. 85. 2015. https://doi.org/10.4025/actascieduc.v37i1.21040.

PERDOMO, W. Estudio de evidencias de aprendizaje significativo en un aula bajo el modelo flipped classroom. Edutec. Revista Electrica de Tecnología Educativa, Palma-España, n. 55, pp. 1–17. 2016. DOI: https://doi.org/1135-9250.

PINO-FAN, L.; PARRA-URREA, Y.; CASTRO-GORDILLO, W. Significados de la función pretendidos por el currículo de. Magis, Revista Internacional de Investigación En Educación, Bogotá-Colombia, v. 11, n. 23, pp. 201–220. 2019. https://doi.org/10.11144/Javeriana.m11-23.sfpc

RAMÍREZ, L. Reflexiones sobre la deserción y la mortalidad estudiantil en las universidades colombiana: Un debate necesario. Educaci y Educadores, Bogotá-Colombia, v.5, pp. 21–38. 2009. Disponible en: <http://educacionyeducadores.unisabana.edu.co/index.php/eye/article/view/509/1596>. Visitado el 20 de febrero de 2019.

RAYAS, J. El reconocimiento de las ideas previas como condición necesaria para mejorar las posibilidades de los alumnos en los procesos educativos en ciencias naturales. Revista Xictli de la Unidad UPD, n. 94. 2004. Disponible en <http://189.208.102.74/u094/revista/54/02.html>. Visitado el 20 de febrero de 2019.

RODRÍGUEZ, L. La teoría del aprendizaje significativo: una revisión aplicable a la escuela actual. Revista Electròica d’Investigació i Innovación Educativa i Socioeducativa, v. 3, n. 1, pp. 29–50. 2011. Disponible en <http://www.in.uib.cat/pags/volumenes/vol3_num1/rodriguez/index. html>. Visitado el 23 de enero de 2019.

SALAZAR, A. Capítulo I: Estrategias de aprendizaje 1. Definición de estrategia de aprendizaje. 1.1. Técnicas y estrategias. Arequipa: Perú. 2004. <http://files.estrategias2010.webnode.es/200000057-48c3e49bde/Microsoft%20 Word%20-%20estrategias-aprendizaje.pdf>. Visitado el 23 de enero de 2019.

SKOVSMOSE, O. Interpretações de Significado em Educação Matemática Interpretations of Meaning in Mathematical Education. Bolema: Boletim de Educação Matemática, São Paulo - Brasil, v. 32, n. 62, pp. 764–780. 2018. https://doi.org/http://dx.doi.org/10.1590/1980-4415v32n62a01

SYCHOCKI DA SILVA, R.; DOS REIS PINTO, S. Funções quadráticas e tecnologías móveis: ações cooperativas em um experimento no ensino médio. Gdola, Ensenza y Aprendizaje de las Ciencias, Bogotá, v. 14, n. 1, pp. 108-125. 2018. https://doi.org/10.14483/23464712.13317

VICENC, F.; GODINO, J. D.; D’AMORE, B. Enfoque ontosemiótico de las representaciones en educación matemática. For the Learning of Mathematics, New Westminster, Canadá, v. 27, n. 2, pp. 2–7. 2