DOI: http://doi.org/10.14483/23464712.12466

LA CONCEPTUALIZACIÓN DE LA EXPERIENCIA DE LA DOBLE RENDIJA A PARTIR DEL ENFOQUE DE CAMINOS MÚLTIPLES DE FEYNMAN

DOUBLE SLIT EXPERIENCE CONCEPTUALIZATION FROM THE VIEWPOINT OF THE FEYNMAN´ MULTIPLE PATHS

A CONCEPTUALIZAÇÃO DA EXPERIÊNCIA DA DUPLA FENDA A PARTIR DO ENFOQUE DE MÚLTIPLES CAMINHOS DE FEYNMAN

María de los Ángeles Fanaro*, Mariana Elgue**

Cómo citar este artículo: Fanaro, M. A y Elgue, M. (2018). La conceptualización de la experiencia de la doble rendija a partir del enfoque de caminos múltiples Feyman. Góndola, Enseñanza y Aprendizaje de las Ciencias, 13(2), 272-290. DOI: http://doi.org/10.14483/23464712.12466

Recibido: 08 de septiembre de 2017 /Aprobado: 01 de febrero de 2018

* Doctora en Enseñanza de las Ciencias por la Universidad de Burgos, España. Trabaja en el proyecto de Investigación en Educación en Ciencias y Tecnología de la Universidad Nacional del Centro de la Provincia de Buenos Aires, Argentina (UNCPBA). Es miembro del Consejo Nacional de Investigaciones Científicas y Técnicas de Argentina (CONICET). Correo electrónico: mariangelesfanaro@gmail.com.

** Doctora en enseñanza de las ciencias (mención física) de la Universidad Nacional del Centro de la Provincia de Buenos Aires, Argentina (UNCPBA). Trabaja en el proyecto de Investigación en Educación en Ciencias y Tecnología de la misma universidad. Correo electrónico: nanaelgue@gmail.com.

Resumen

En este trabajo se presenta un análisis de la conceptualización de un grupo de estudiantes con relación a la reformulación cuántica de la experiencia de la doble rendija. Se realizó una categorización inductiva de las resoluciones de N=83 estudiantes de dos escuelas secundarias en las que se implementó una secuencia didáctica dedicada a enseñar aspectos fundamentales de mecánica cuántica. Utilizando la teoría de los campos conceptuales de Vergnaud se identificaron posibles teoremas en acto que obstaculizaron o facilitaron la conceptualización, en las situaciones que requerían la técnica de considerar caminos alternativos de Feynman e interpretar sus resultados desde este marco cuántico. Del análisis presentado se concluye que las situaciones resultan accesibles a los estudiantes del penúltimo año de la escuela secundaria, ya que más de la mitad de ellos logró reformular cuánticamente la experiencia de la doble rendija. Los obstáculos detectados en los estudiantes indican que algunas situaciones podrían modificarse para evitarlos, y así favorecer la conceptualización. También se plantea la posibilidad de ampliar la secuencia para cubrir otros conceptos como difracción y principio de incerteza, bajo el mismo enfoque.

Palabras clave: conceptualización, física, enseñanza, secundaria; cuántica.

Abstract

In this work, we analyze the conceptualization of a student’s group about the quantum reformulation of the double slit experiment. In an inductively way we categorized the resolutions of 83 students from two secondary schools after implementing a complete sequence to teach basic quantum mechanics. By the Vergnaud´s conceptual fields theory, a set of possible theorems in act were identified in those situations which required to apply the multiple paths technique and to interpret the results from this quantum frame. These theorems in act were categorized as obstacles or enablers to the students´ conceptualization. From the analysis done, it is concluded that the situations seem to be accessible to these high school students since more than half made the quantum reformulation of the double slit experiment as it was expected. Regarding the obstacles detected, they indicate that some situations could be modified to be avoided, and thus to favor the conceptualization. It also raises the possibility of extending the sequence to cover other concepts such as diffraction and uncertainty principle, under the same approach.

Keywords: conceptualization, physics, teaching, secondary, quantum.

Resumo

Neste trabalho apresentamos uma analise da conceptualização de uma turma de estudantes respeito da reformulação quântica do experimento da dupla fenda. Fizemos uma categorização indutiva dos depoimentos de 83 estudantes de duas escolas de secundaria nas quais implementamos uma sequencia didática visando ensinar aspetos fundamentais de Mecânica quântica. Por meio da teoria dos campos conceituais de Vergnaud identificamos possíveis teoremas em ato que impediram ou facilitaram a conceptualização, nas situações que precisavam de aplicar a técnica de considerar caminhos alternativos de Feynman e ainda interpretar seus resultados desde este marco quântico. Concluímos que as situações são accessíveis aos estudantes do penúltimo ano de escola secundaria, par quanto mais da metade dos estudantes conseguiu reformular quanticamente o experimento da dupla fenda. Os obstáculos detectados nos estudantes indicam que algumas situações poderiam modificar-se para os evitar e assim favorecer a conceptualização. Também, vimos a possibilidade de ampliar a sequencia para tratar outros conceitos como difração e principio de incerteza, com o mesmo enfoque.

Palavras chaves: conceptualização, física, ensino, secundaria, quântica.

Introducción

Este trabajo forma parte de una investigación más amplia en la que proponemos el estudio de ideas básicas del campo conceptual de la física cuántica (no relativista) en la escuela secundaria. Desde el campo de la investigación en la enseñanza de las ciencias, la preocupación por el problema de la enseñanza de la física cuántica ha estado presente en la agenda de los investigadores, pero siempre desde un enfoque canónico (BUNGUM, et al. 2015; CABRAL DE PAULO, MOREIRA, 2005; CUPPARI et al. 1997; FISCHLER, LICHTFELDT, 1992; GONZÁLEZ, FERNÁNDEZ, SOLBES, 2000; LOBATO, GRECA, 2005; GRECA, MOREIRA, HERSCOVITZ, 2001; HADZIDAKI, 2008; HENRIKSEN et al., 2014, 2015; MONTENEGRO, PESSOA, 2002; IRESON, 2000; MÜLLER, WIESNER, 2002; MANNILA, KOPONEN, NISKANEN, 2002; NIEDDERER, 1996; OLSEN, 2002; OSTERMAN, MOREIRA, 2000; OSTERMANN, RICCI, 2004; PESSOA, 1997; PINTO, ZANETIC, 1999; ZOLLMAN, 1999). Otras investigaciones, en cambio, han adoptado el enfoque de caminos múltiples de Feynman (FEYNMAN, 1985) para abordar la enseñanza de la mecánica cuántica, utilizando herramientas computacionales (TAYLOR et al. 1998; OGBORN, HANC, TAYLOR, 2006; DOWRICK, 1997; HANC, TULEJA, 2005; MALGIERI, ONORATO, DE AMBROSIS, 2015; KRIJTENBURG-LEWERISSA, BRINKMAN, JOOLINGEN, 2017). En general, estas propuestas han sido formuladas para el nivel universitario, se centran en el comportamiento dual de la luz y utilizan el concepto de fotón.

Ante el problema de enseñar conceptos básicos de mecánica cuántica con sentido y sin paradojas para los estudiantes de la escuela secundaria (HOBSON, 2007), proponemos utilizar el enfoque de caminos múltiples de Feynman para el estudio del comportamiento de los electrones y de la radiación electromagnética. Su potencial didáctico ya ha sido analizado en nuestros trabajos previos en los cuales propusimos dos secuencias didácticas utilizando este enfoque, las que fueron implementadas en varios cursos de la escuela secundaria (FANARO, OTERO, ARLEGO, 2007; FANARO, OTERO, 2008; FANARO, ARLEGO, OTERO, 2012a; 2014; FANARO, ELGUE, ARLEGO, 2016; FANARO, ELGUE, OTERO, 2016; 2016c; FANARO et al. 2017).

Desde el enfoque de caminos múltiples de Feynman diseñamos e implementamos una secuencia de situaciones con estudiantes de dos escuelas secundarias de la ciudad de Tandil (Buenos Aires, Argentina), destinada al estudio de la radiación electromagnética, en particular de la luz, desde un marco cuántico. Además del nivel educativo de los estudiantes, esta secuencia supone una diferencia respecto de las propuestas mencionadas antes, ya que aquí se busca enfatizar el concepto clave de probabilidad y superposición, por lo cual no se considera necesario referirse al fotón. Por otro lado, no se plantean cuestiones ontológicas acerca de la luz, sino que se busca describir, explicar y predecir el comportamiento de la luz en situaciones tanto cotidianas como experimentales específicas. Esta secuencia posiblemente produzca cambios en el concepto de luz que tienen los estudiantes, pero este aspecto queda fuera de los objetivos de este trabajo.

Para conocer la viabilidad de esta secuencia analizamos las dificultades y facilidades para la conceptualización que emergen cuando los estudiantes afrontan las situaciones propuestas. En este trabajo en particular buscamos responder: ¿Cómo describir el proceso de la conceptualización de los estudiantes con relación a la reformulación cuántica de la experiencia de la doble rendija (EDR)? Realizamos este análisis en forma global, para el grupo de estudiantes en su totalidad, dado el volumen de datos (N=83 estudiantes).

1. Marco teórico

Realizamos este análisis a partir de la teoría de los campos conceptuales de Vergnaud (VERGNAUD, 1990, 1994, 2013), dado que esta teoría ofrece elementos que permiten analizar el dominio de los conceptos relativos al comportamiento cuántico por parte de los estudiantes al resolver las situaciones presentadas en la secuencia propuesta.

Desde la teoría de los campos conceptuales, la actividad de los estudiantes cuando se enfrentan a una situación está estrechamente relacionada con sus esquemas y con el uso de los invariantes operatorios –conceptos en acto y teoremas en acto– que organizan la actividad en esa situación. Un concepto en acto es definido por Vergnaud como una categoría que se considera relevante para la situación que se está afrontando y un teorema en acto es entendido como una proposición que se tiene como verdadera respecto a esa situación. Estos teoremas en acto y conceptos en acto, denominados invariantes operatorios, a diferencia de los conceptos y teoremas científicos, que son siempre explícitos y se puede analizar su pertinencia y su validez, se mantienen generalmente implícitos en la acción y son funcionales (útiles) a la resolución de cada situación, en cada estudiante. El análisis de la acción no se focaliza en el análisis de la conducta, sino que es necesario considerar la actividad del sujeto en situación (VERGNAUD, 1990), puesto que los estudiantes se basan en su conocimiento implícito para reconstruir el conocimiento científico explícito, siendo este un proceso progresivo y de largo plazo (OTERO, 2014).

Los invariantes operatorios son parte del triplete que forman los conceptos, junto con las situaciones y las representaciones simbólicas propias del concepto. Por tanto, su uso cumple un papel esencial en la conceptualización, entendida como el proceso mediante el cual se reconocen e identifican los objetos con sus relaciones, propiedades y transformaciones.

Metodológicamente haremos uso de la idea de Vergnaud, cuando destaca que en las disciplinas científicas y tecnológicas es más útil identificar qué teoremas en acto pone en juego un estudiante para afrontar una situación, más que afirmar que un estudiante comprendió un concepto.

2. Metodología

2.1 Contexto y características del grupo de clases

Se implementó una secuencia de situaciones en cuatro cursos públicos de gestión privada del penúltimo año de la escuela secundaria (16-17 años). El plan de estudios de los cursos establece dos encuentros semanales, uno de una hora y el otro de dos horas para la asignatura física. Se trata de una muestra intencional, puesto que la selección de los cursos se realizó con el criterio de que el investigador fuese el profesor, para que puedan controlarse las variables: tiempo, conocimiento de los estudiantes, articulación con otros contenidos, familiaridad con las condiciones institucionales, y posibilidad de replicar en los cuatro cursos la misma secuencia de situaciones. Las cuatro implementaciones que se realizaron se consideran representativas pues reúnen las características de clases habituales de física de la escuela secundaria argentina. Los estudiantes de las cuatro implementaciones se consideran un solo grupo, puesto que tienen características socioculturales similares, y ninguno había estudiado hasta el momento física cuántica ni el comportamiento de la luz en distintas situaciones, razón por la cual se decidió asumir como conocimientos previos aquellos relacionados con el reconocimiento y la descripción de las experiencias cotidianas de la reflexión especular de la luz, o la refracción de la luz. El propósito de la secuencia implementada fue reformular una descripción de los fenómenos relativos a la luz desde el modelo más ampliamente aceptado por la comunidad de los físicos actuales: la teoría cuántica. La EDR tiene aquí un rol predominante, y en lugar de utilizarse como comúnmente se lo hace –para comprobar el carácter ondulatorio de la luz en términos de interferencia y difracción– se la propuso para formular una explicación de la experiencia realizada en la clase con los estudiantes, utilizando los conceptos y principios de la mecánica cuántica. La secuencia completa y su análisis didáctico previo pueden consultarse en FANARO, ELGUE, ARLEGO (2016) y FANARO ELGUE, OTERO (2016).

La parte de la secuencia analizada para los objetivos de este trabajo, se enfoca en aquellas situaciones donde se requería aplicar la técnica de Feynman (llamada con los estudiantes considerar los caminos alternativos, abreviada como CCA) en la EDR, su interpretación y su contrastación con los resultados experimentales que los estudiantes obtienen al realizar la experiencia. La EDR se realizó en clase con luz láser, y también se presentó a los estudiantes un conjunto de imágenes de la experiencia donde se puede apreciar que la luz llega a la pantalla en forma discreta y finalmente se distribuye formando un patrón claramente reconocible de zonas de máximas y mínimas concentraciones. Se presenta como modelo que explica ambas situaciones con luz, el modelo de CCA, que es una adaptación del modelo original path integrals de Feynman (FEYNMAN, HIBBS, 1965).

El trabajo de transformación del saber desde el saber sabio al saber enseñado reconocido como la transposición didáctica (CHEVALLARD, 1985) se hace presente cuando se formulan las situaciones para que los estudiantes puedan otorgarles sentido a los conceptos cuánticos. También interviene en la elección de las experiencias para realizar o analizar en clase, como en la presentación del modelo de Feynman, reemplazando las integrales por sumas de vectores, como en las preguntas para los estudiantes. Así, la secuencia completa propone realizar en aula experiencias sencillas de reflexión, refracción de la luz, utilizando una fuente de luz láser. También se propone analizar los resultados de la EDR si esta se realizara bajo condiciones experimentales tales que se noten detecciones individuales que con el tiempo forman el mismo patrón de franjas. Luego, como marco explicativo de todas las experiencias se propone el de CCA, comenzando con la descripción de la emisión y detección de la luz como el caso más sencillo. Esto permite abordar la idea de la superposición, característica inherentemente cuántica, que en este caso se trata de considerar los caminos alrededor del camino clásico para el cálculo de la probabilidad. Luego, la secuencia propone reformular las mismas experiencias desde este modelo.

La secuencia requería que los estudiantes trabajaran en forma grupal, conversando sobre cada problema e intentando consensuar luego una respuesta escrita. Por su parte, el papel del profesor fue presentar las situaciones, proponer las preguntas y coordinar las acciones del grupo de clase: gestionar el tiempo didáctico permitiendo el trabajo autónomo de los grupos, dirigir la puesta en común de cada grupo, señalar los consensos y los desacuerdos, y de ser necesario, introducir el conocimiento que podría hacer falta, aparte del que conlleva la situación. Al finalizar la implementación (aproximadamente 20 horas de clase para desarrollar las 13 situaciones) se propuso una última situación (S14), en la que se pedía la elaboración de una síntesis personal. Esta instancia tiene especial relevancia para el análisis que realizamos aquí, ya que consideramos que allí expresaron lo que a juicio de cada estudiante fue más importante de las clases. Se analizaron las situaciones S11 a S14 como se expone a continuación.

2.2 Las situaciones analizadas

Previo a las situaciones que se analizan en este trabajo, se plantearon las experiencias de reflexión, refracción y experiencia de la doble rendija con luz. En todos los casos, se comenzó por situaciones de predicción de resultados por parte de los estudiantes, y luego se propuso la realización experimental en aula. Se presentó la técnica CCA a los estudiantes, dentro del modelo de la mecánica cuántica como marco para todas las experiencias presentadas, producto del análisis de una adecuada transposición didáctica.

Situación 11: la técnica CCA aplicada a la EDR (tal como se presentó a los estudiantes)

Analicemos la experiencia de la doble rendija, considerando las detecciones individuales de la luz. Recordemos que, al principio, las detecciones de la luz parecían ser aleatorias, es decir no se notaba en la pantalla ninguna formación en particular, pero al pasar el tiempo, se comenzaba a notar una distribución, donde había lugares con gran cantidad de detecciones, y lugares donde no había, o había muy pocas, detecciones de luz. Nos preguntamos ahora: ¿Cómo calcular la probabilidad de detectar la luz para cada lugar de la pantalla? La teoría indica que debemos utilizar para ello la técnica de considerar los caminos alternativos de la mecánica cuántica. En la figura siguiente se presenta un esquema de la experiencia, para poder analizar la cuestión de cómo determinar la probabilidad de detectar luz en determinado lugar de la pantalla, a cierta distancia, digamos x, del centro de la pantalla.

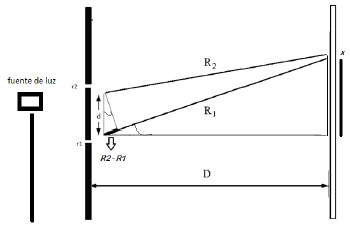
Sabemos, de la primera vez que calculamos la técnica para el caso más simple (luz que va de un punto inicial dado a otro punto final dado) que los vectores que entran en la consideración de la probabilidad, son los vectores identificados con el camino directo (que es el más corto) y un conjunto finito de vectores asociados a los caminos cercanos, digamos “N”. Es decir, en el cálculo de la probabilidad habrá que considerar N veces el vector cuyo ángulo es proporcional al tiempo mínimo, al cuadrado:

Recordemos que k es una constante de proporcionalidad que depende del color de la luz y del medio en el que la luz se propaga. Como en este caso se trata de aire, la constante solo depende del color de la luz.

También es posible anotar este vector utilizando la notación de coordenadas:

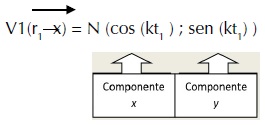
Para la otra rendija, en forma análoga tenemos que

Ahora, debemos hacer la suma de los dos vectores (1) y (2),

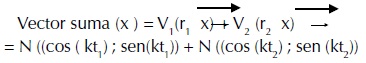
Realizando en forma analítica la suma de los vectores, y luego elevando el resultado al cuadrado, se obtiene la siguiente expresión para la detección de la probabilidad en determinado lugar x del centro de la pantalla:

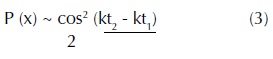
Para expresar la probabilidad en función de la geometría de la situación, reemplacemos en (3) el tiempo por la distancia sobre la velocidad (en este caso es c la velocidad de la luz) para cada caso: t2=R2 /c y t1=R1 /c. Por tanto, kt2 - kt1 = R2 /c - R1 /c = (R2- R1)/c (ver esquema de la experiencia en la fig. I).

Entonces, la expresión final queda:

Podemos realizar aún más consideraciones geométricas para expresar la diferencia de caminos R2 - R1 de (4) en términos de la distancia entre las rendijas (d) o la distancia a la pantalla de detección D, y suponemos que D>>d:

Reemplazando esto en la ecuación de P(x) llegamos a la expresión:

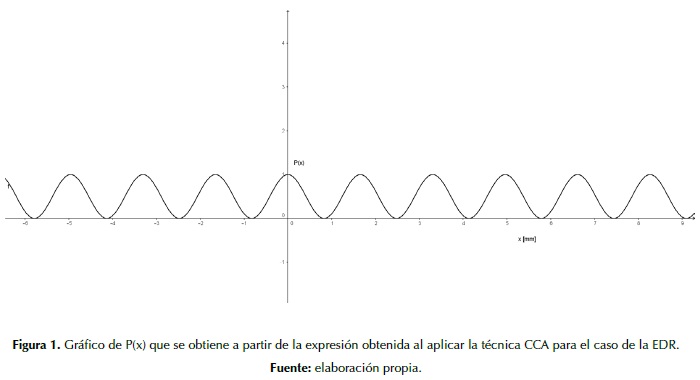
La expresión matemática (5) representa la probabilidad de detectar luz a una distancia x del centro de la pantalla, que predice la técnica de considerar caminos alternativos. Debemos analizar si esta predicción es acorde a lo que obtuvimos al realizar la experiencia en clase.

Grafica la función P(x) de la expresión (5), y describe cómo varía la probabilidad según la distancia al centro de la pantalla, x. Aproxima los valores experimentales para D (distancia desde las rendijas hasta la pared) y d (distancia entre rendijas) y el valor de la constante de proporcionalidad k, que corresponde al color del láser rojo es k= 430.1012(s^-1).

Se planteó esta situación para que los estudiantes analizaran las características de la función de probabilidad, para luego establecer relaciones con los resultados experimentales. Esta situación requería que los estudiantes conocieran y aplicaran nociones sobre las funciones trigonométricas previas, así como forma de una función armónica, ceros, máximos y mínimos. Como parte de la transposición didáctica se decidió trabajar con la expresión (5) que, si bien es aproximada, permite que los estudiantes den sentido a las características de la función P(x).

Por ejemplo, si se establecen los valores D=3000 mm, d=3 mm, y se considera c=3,1011 m/s, y k= 430,1012s-1, se obtiene un gráfico para P(x) como se muestra en la figura 1, en donde los valores máximos y mínimos coinciden aproximadamente con los resultados obtenidos en la experiencia en el aula, donde la separación entre máximos y mínimos es del orden del milímetro.

A partir del reconocimiento de las características de esta función, se esperaba que los estudiantes interpretaran que, por un lado, como la función solo toma valores positivos, esto es acorde con cada valor que puede tomar la probabilidad, y por otro, que la función toma valores máximos y mínimos en forma periódica. Asimismo, se esperaba que ellos notaran que un máximo en la función se corresponde con la probabilidad máxima de detección, mientras que un mínimo en la función se corresponde con la probabilidad de detección nula.

Para que los estudiantes establecieran la correspondencia entre los máximos y mínimos de probabilidad graficada en la situación 11, con los resultados de la EDR que muestra las detecciones individuales, se solicitó lo siguiente:

Situación 12: interpretación de los resultados de la EDR en pantalla desde la teoría cuántica (tal como fue presentada a los estudiantes)

Relaciona los valores máximos y mínimos de la función P(x) que dibujaste recién, con las detecciones que se observan experimentalmente al realizar la experiencia de la doble rendija.

Aquí se esperaba que los estudiantes construyeran la idea que un máximo en la función de probabilidad indica una probabilidad máxima de detección de luz en ese lugar de la pantalla. Por el contrario, un mínimo en la función de probabilidad indica que en ese lugar la probabilidad de obtener detecciones de luz es mínima, es decir, se trata de una franja de oscuridad.

Situación 13. Interpretación de los resultados de la EDR aplicando la técnica CCA (tal como fue presentada a los estudiantes)

Para analizar gráficamente la suma de los vectores asociados a cada rendija y obtener la probabilidad en cada punto de la pantalla, ejecuta la simulación “EDR”.

a) Describe aquí algunas de las imágenes obtenidas al correr la simulación.

b) Analiza lo que va ocurriendo con los vectores asociados a cada camino, con la suma y con la formación de la función de P(x) que se muestra a la derecha.

Aquí se esperaba que los estudiantes identificaran que, en cada lugar de la pantalla de detección de la EDR, la probabilidad se calcula con el aporte de dos vectores: los asociados a los dos caminos principales para la luz (que unen cada rendija con el punto de detección x), ya que el resto de los caminos, alejados de ellos, no contribuyen a la suma (por tener ángulos muy diferentes).

Para esta situación construimos una simulación con Modellus™, en la cual se va mostrando la construcción del gráfico de la función P(x) para cada valor de x, y simultáneamente se van dibujando los dos vectores principales que aportan al cálculo de probabilidad. En la figura 2, se presentan algunas de las pantallas que brinda la simulación.

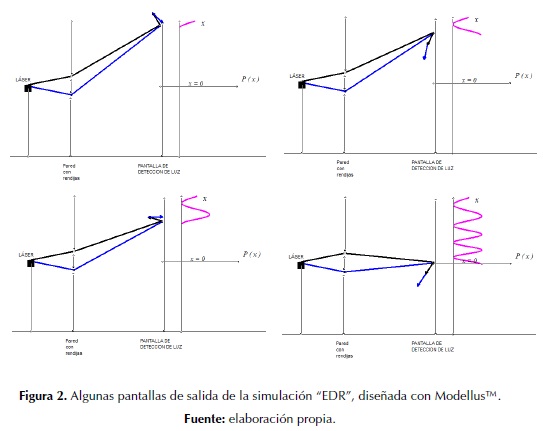
Se esperaba que los estudiantes noten que en aquellos lugares donde la suma de los dos vectores se anula, al tener ambos la misma dirección y sentido opuesto, la función P(x) tiene un mínimo y, por el contrario, la suma resulta máxima cuando los vectores se encuentran colineales, y entonces la función tiene un máximo.

Situación 14: elaboración de una síntesis personal

Realiza una síntesis personal de los conceptos e ideas estudiados en estas clases de física dedicadas al estudio de la luz. Coloca aquellos conceptos, ideas, experiencias y explicaciones que consideres más importantes desde tu punto de vista. Puedes incluir gráficos, esquemas, fórmulas, etc. Extensión máxima: una hoja.

2.3 Construcción de las categorías y subcategorías

Según los objetivos de la secuencia propuesta y la pregunta formulada en este trabajo, se construyeron dos categorías de análisis y tres subcategorías para cada una. En la primera categoría se analizaron situaciones propias de la secuencia (S11 y S13) y en la segunda, situaciones de la secuencia y de la síntesis (S12, S13 y S14). Incluimos el análisis de la síntesis en esta categoría porque consideramos que si, además de reformular cuánticamente la EDR en las primeras situaciones, lo hicieron también en la síntesis personal, esto constituye un indicador de una conceptualización acorde a lo esperado. El criterio de construcción de ambas categorías se corresponde con la estructura de la secuencia didáctica propuesta, y en este caso surgió de la necesidad de comprender cómo los estudiantes conceptualizaron, por un lado, la técnica del cálculo de probabilidades aplicada a la EDR (categoría T) que requería relacionar la expresión matemática obtenida con la técnica, con una curva de probabilidad. Por su parte, se buscaba conocer de qué forma los estudiantes reformularon cuánticamente la experiencia, es decir si lograron vincular el modelo matemático con los resultados experimentales conocidos (categoría R). Dada la distinta complejidad de la conceptualización requerida en ambos casos, se formularon las siguientes categorías y subcategorías.

a. Técnica CCA en relación a la curva de probabilidad para la EDR (T)

En las situaciones analizadas, los estudiantes debían graficar la función P(x) obtenida algebraicamente y a partir de ella, vincular los caminos posibles, sus vectores asociados, la contribución de los dos vectores asociados a los caminos de tiempo mínimo y su suma, con las características del gráfico de P(x) construido. Es decir, la complejidad de esta situación radica en que requiere que los estudiantes vinculen la representación algebraica y funcional de la probabilidad con la representación geométrico-vectorial.

En la subcategoría T₁, se agrupan las resoluciones en las cuales las producciones son escasas y no se utiliza la suma de la técnica CCA para explicar las características del gráfico P(x).

La subcategoría T₂ agrupa las resoluciones en las cuales los estudiantes interpretan los máximos de la curva como la máxima probabilidad de detección, pero no lo justifican desde la suma de los vectores. Es decir, son resoluciones donde se describe la curva P(x) con máximos y mínimos, justificándolos de manera incompleta o en desacuerdo con lo que se buscaba que los estudiantes conceptualizaran.

La subcategoría T₃ agrupa las resoluciones en las cuales, desde sistemas de representación verbal y gráfico complejos, los estudiantes establecen las relaciones adecuadas entre vectores, caminos, sumas, máximos y mínimos de P(x), conceptualizando así que cuando la suma de los dos vectores asociados a los dos caminos principales es la mayor posible, representa un máximo en la curva.

b. Reformulación cuántica EDR (R)

Esta categoría se construyó a partir del análisis de las resoluciones donde los estudiantes debían reformular cuánticamente los resultados de la EDR, es decir interpretar los resultados en términos de probabilidades de detección, vinculando el gráfico de P(x) con los resultados experimentales de la EDR.

La subcategoría R₁ incluye aquellas resoluciones donde las representaciones verbales y pictóricas son escasas y no permiten realizar una inferencia acerca de la conceptualización. También agrupa aquellas resoluciones donde los estudiantes reformulan la ECR, relacionando los valores máximos y mínimos de P(x) pero solamente con las zonas de claros y oscuros en el resultado de la EDR y no en términos de probabilidad, como se esperaba.

La subcategoría R₂ agrupa las resoluciones en donde explica la presencia de franjas de máximos y mínimos de intensidad de luz a partir de la función de P(x). Utilizando representaciones verbales y gráficas adecuadas, establecen en las situaciones de la secuencia, que los máximos de la función P(x) se corresponden con una probabilidad de detección máxima, señalando así las zonas de luz en los resultados de la EDR. Por su parte también hacen corresponder los mínimos de la curva de P(x) con la menor detección de probabilidad, señalados como los lugares de oscuridad en los resultados para la EDR obtenidos. Sin embargo, en la instancia de síntesis estos mismos estudiantes solo mencionan la EDR sin realizar una reformulación cuántica de los resultados, como se esperaba.

Finalmente, R₃ incluye las resoluciones que reformulan cuánticamente la EDR, es decir, interpretan los lugares de luz y oscuridad de la pantalla, en términos de probabilidades de detección, y también lo destacan en la elaboración de síntesis personal.

3. Presentación de resultados y discusión

Los resultados obtenidos mediante la categorización inductiva, se presentan en la tabla 1. Se encontró un agrupamiento que permite explicar distintos niveles o grupos de conceptualización, y conjuntamente con la categorización de las respuestas de los estudiantes, se identifican algunos teoremas en acto que los estudiantes podrían estar utilizando al resolver las tareas, que se consideran como representativos de cada grupo. La categorización realizada y los teoremas en acto suponen un gradiente en la conceptualización, para permitir identificar los obstáculos y las facilidades para el proceso de conceptualización.

Un conjunto de n₁=12 resoluciones presenta representaciones verbales muy breves, en ocasiones incoherentes con lo solicitado en la actividad, y en el caso de realizar las gráficas estas resultaron ser muy incipientes, por tanto, es difícil identificar la presencia de teoremas en acto, lo que estaría indicando una conceptualización pobre. Al no aplicar la técnica CCA a la EDR y no establecer la relación correcta entre los vectores principales, la suma y la probabilidad de detección, los estudiantes no pueden reformular la EDR en términos cuánticos. Esto permite reafirmar la importancia de la técnica para la conceptualización, como se sostiene desde la perspectiva abordada en este trabajo, ya que el uso de la técnica CCA constituye el punto clave para que el estudiante comprenda que, del conjunto infinito de caminos posibles, solo son dos los que deben considerar en la suma, y que depende del resultado de la suma de ellos, la probabilidad de detección de luz en la pantalla.

A diferencia del primer grupo, en n₂=21 resoluciones se utiliza la técnica de manera incompleta (T₂) dado que los estudiantes se refieren a la probabilidad de los caminos, en lugar de referirse a la probabilidad de detección de luz para cada lugar de la pantalla donde se detecta la luz. Esto representa una mejora en la conceptualización respecto al grupo 1 porque los estudiantes hacen referencia a la probabilidad, es decir las resoluciones presentan una reformulación de la EDR (R₂) en términos de probabilidad de detecciones en la pantalla, lo cual es muy positivo para la conceptualización buscada. Los teoremas en acto utilizados en estas resoluciones resultaron ser incompletos, y hasta en algunas ocasiones incorrectos, en cuyo caso resultaría un obstáculo, aunque en ambos casos salvables en términos de conceptualización. Por ejemplo, un teorema en acto que fue identificado y que resulta un obstáculo para la conceptualización de la reformulación cuántica es el siguiente:

TeA Camino-probabilidad: En la curva de P(x) los valores más bajos de P representan los caminos menos probables para que llegue la luz, y los valores más altos de P representan los caminos más probables para que llegue la luz.

La figura 3 presenta una resolución típica de este grupo de conceptualización, donde se puede identificar el uso de este teorema en acto, como resolución a la consigna de relacionar los valores máximos y mínimos de la función P(x) de la función graficada (obtenida mediante la aplicación de la CCA), con las detecciones que se observan experimentalmente al llevar a cabo la experiencia de la doble rendija.

Consideramos que el uso de este teorema en acto estaría obstaculizando la conceptualización, ya que el estudiante confunde la probabilidad de detección de luz, con la probabilidad de los caminos.

También identificamos en este grupo de conceptualización el siguiente teorema en acto, que, si bien no es incorrecto, no está completo:

TeA Detección-probabilidad: Un máximo en la función P(x) corresponde con probabilidad de detección máxima, lo que significa una concentración máxima de detecciones, y un mínimo en la función corresponde con probabilidad cero, lo que significa que no hay detecciones.

Un protocolo representativo del uso de este teorema en acto se presenta en la figura 4. Se trata de la respuesta del estudiante A5 ante el problema de analizar lo que va ocurriendo con los vectores asociados a cada camino, con la suma y con la formación de la función de P(x) a partir de una simulación realizada con Modellus™. En la simulación se va construyendo el gráfico de la función P(x) para cada valor de x, y simultáneamente se dibujan los dos vectores principales que aportan al cálculo de probabilidad, en forma dinámica, cubriendo todas las posiciones de la pantalla.

Como se observa, este teorema en acto no es incorrecto en el sentido que no obstaculiza la conceptualización, aunque es incompleto, porque indica que los estudiantes están muy cerca de establecer la relación adecuada entre la probabilidad de detección con los valores máximos y mínimos de la curva P(x) obtenida al aplicar la técnica CCA a la experiencia de la doble rendija.

Un grupo de n₃= 17 resoluciones a diferencia del grupo anterior, indica una mejor conceptualización de la técnica y de su relación con la curva de probabilidad (T₃), aunque la reformulación cuántica de la EDR no se llega a hacer explícita en la síntesis personal (R₂). Identificamos como teorema en acto representante de este grupo de conceptualización:

TeA Vector-probabilidad: En el gráfico de la función P(x) obtenido al reemplazar los distintos valores, cuanto más pequeña es la suma de vectores la función P(x) tendrá un mínimo, y cuanto más grande la suma, la función P(x) tendrá un máximo

En el protocolo de la figura 5 se presenta una resolución donde es posible identificar el uso de este teorema en acto, como resolución de la situación que utilizaba el Modellus, comentada antes.

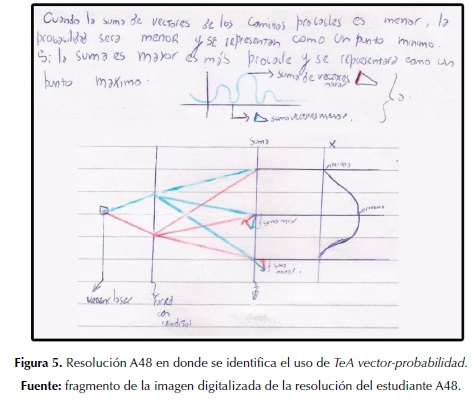
Usando este teorema en acto los estudiantes explicaron el gráfico en términos de los vectores asociados a los caminos principales. Es notorio en esta resolución el énfasis colocado en la correspondencia gráfica del vector resultante con los lugares de la curva y los máximos y mínimos de la función de probabilidad. Esto constituye un resultado alentador respecto al uso de la técnica, y su relación con el gráfico de P(x).

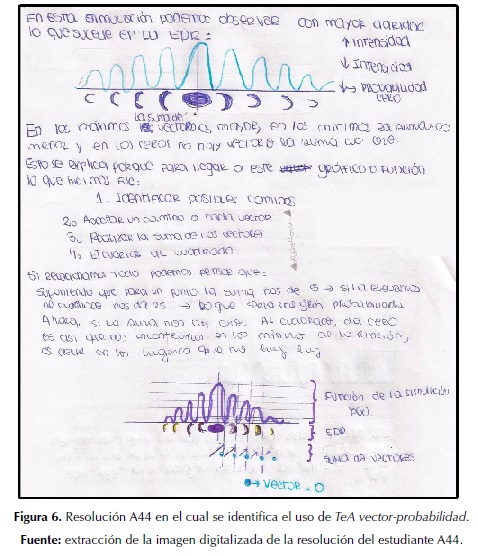
Un último conjunto de resoluciones, n₄=33 agrupa las resoluciones de los estudiantes que, utilizando teoremas en acto apropiados para la conceptualización, muy cercanos a los científicos (TeA vector-probabilidad) reformularon cuánticamente la EDR (T₃) enfatizándolo además en la síntesis personal (R₃). Es necesario resaltar el uso espontáneo de más de un sistema de representación de algunos estudiantes de este grupo de respuestas (representaciones gráficas de las experiencias) para complementar, detallar y mejorar las explicaciones cuánticas formuladas, como un buen indicador de la conceptualización alcanzada, puesto que esto requiere una alta abstracción y manejo de representaciones externas por parte de los estudiantes. Un ejemplo típico de este grupo de conceptualización se presenta en las figuras 6 a 8.

La figura 6 presenta la resolución de A44 en la situación de reformular cuánticamente la EDR con ayuda de la simulación con Modellus. En este caso, el estudiante reconstruyó el gráfico de salida de la simulación, superponiendo los resultados experimentales obtenidos al realizar la experiencia en clase (el círculo central representando el máximo central y las líneas laterales a los máximos secundarios). También reforzó la representación superponiendo (parte inferior del dibujo) un vector resultante, que toma diferentes longitudes en correspondencia con los distintos lugares de la distribución de probabilidad y de zonas de máximos y mínimos. Destacamos que esta representación nunca fue presentada en la situación, sino que es una espontánea.

La figura 7 ilustra el fragmento de la síntesis personal elaborada por el mismo estudiante, A44, en el cual resalta la reformulación cuántica, de forma espontánea y con detalle.

La figura 8 presenta la resolución de A26 en la instancia de síntesis. En este caso, de forma narrativa y sin realizar ninguna representación gráfica, el estudiante reformuló cuánticamente la EDR relacionando la resultante de los vectores asociados a los caminos principales, con los máximos y mínimos de la función de probabilidad y los resultados experimentales. Esta resolución de elaboración personal tan rica y compleja por parte del estudiante estaría indicando la conceptualización buscada con la secuencia.

En la figura 9 se presenta la distribución de frecuencias de los estudiantes por grupos de conceptualización. Estos cuatro grupos no se refieren a los cuatro cursos donde se implementó la secuencia, sino que son grupos de resoluciones, que fueron formulados a partir de los resultados obtenidos con la categorización inductiva realizada en este trabajo.

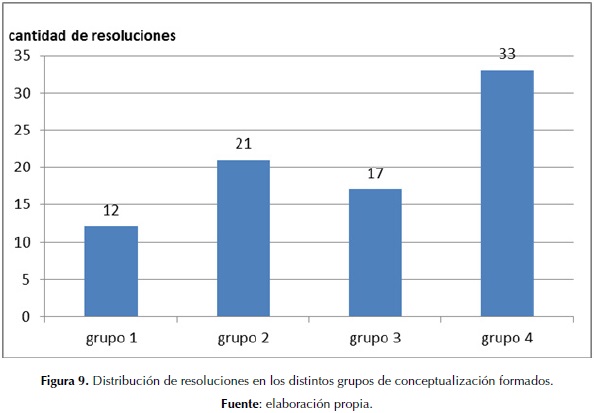
A partir del análisis realizado y el gráfico obtenido, es posible apreciar un gradiente de conceptualización en las resoluciones, donde en un extremo se ubican las (n₁=12) resoluciones que indicarían la presencia de dificultades para la conceptualización, dados los obstáculos identificados con los teoremas en acto (obstaculizadores), y en otro extremo, un grupo de resoluciones que indicaría qué conceptualización fue acorde con las expectativas y los objetivos de la secuencia. Los grupos del medio representan un indicador de los distintos obstáculos que los estudiantes encontraron para usar la técnica y reformular cuánticamente la EDR, que señalan la necesidad de reformular algunas situaciones, e incluir otras que ayuden a superar estos obstáculos. Desde el análisis de la viabilidad de la secuencia es alentador que entre los dos últimos grupos (más de la mitad del total de los estudiantes) lograron explicar cuánticamente los resultados de la EDR. En este sentido, es posible afirmar que la secuencia resultó viable.

4. Conclusiones y perspectivas

Ante la necesidad de que los estudiantes de la escuela secundaria aprendan nociones básicas de mecánica cuántica con sentido, que más adelante podrá ser retomado y profundizado, el trabajo de transposición didáctica, realizado y plasmado en la secuencia de situaciones, es esencial. La decisión de adoptar el método de Feynman de Caminos Múltiples se basa en sus ventajas potenciales que solo pueden ser evaluadas mediante su implementación efectiva. En este caso, se trató de que los estudiantes conocieran los fundamentos de mecánica cuántica, relativos a la probabilidad y a la superposición, para el caso de una experiencia crucial como la experiencia de la doble rendija.

Los resultados de esta investigación nos permiten concluir que la técnica de CCA, basada en el enfoque de Feynman, como la secuencia lo propone, resulta accesible a los estudiantes del anteúltimo año de la escuela secundaria, aunque los obstáculos detectados indican que la secuencia debe reformularse. Por ejemplo, se pueden incluir simulaciones donde los estudiantes puedan seleccionar distintos caminos, y además de visualizar cada vector asociado, se vaya dibujando la suma, y simultáneamente se muestre el valor de la probabilidad relativa. En este sentido, se están diseñando estas simulaciones con planillas de cálculo con la ventaja de no necesitar software específico. Suponemos que la secuencia propondrá más facilitadores para la conceptualización, evitando así los obstáculos, si se complementa el trabajo algebraico con una exploración vectorial mayor que la que se propone en la secuencia actual.

Conocer los obstáculos y ayudas a la conceptualización que se producen en los estudiantes cuando enfrentan las situaciones, es clave para conocer el funcionamiento de la secuencia didáctica propuesta. Los resultados expuestos aquí fueron obtenidos cualitativamente mediante la categorización inductiva, pero consideramos que un análisis de los datos discursivos textuales (por ejemplo, realizado con un análisis factorial de correspondencias simples) complementaría este análisis y generaría mayor conocimiento acerca de las representaciones verbales que utilizan los estudiantes. Aunque desde nuestro marco teórico asumimos que el concepto no es solamente la significación de las palabras, la enunciación o puesta en palabras o en símbolos gráficos cumple un rol importante, incluso decisivo en los procesos de conceptualización (MOREIRA, 2007). Este análisis constituirá un complemento al estudio para describir la evolución de las representaciones (junto con las situaciones y los invariantes operatorios que forman parte de los conceptos) que será próximamente realizado.

Otras líneas de acción que resultan de este trabajo consisten, por un lado, en la necesidad de estudiar qué modificaciones de las situaciones deberían realizarse con el fin de evitar los obstáculos detectados aquí, y realizar nuevas implementaciones para analizar cómo esto impacta en la conceptualización. Por otro lado, se propone ampliar la secuencia de situaciones para que los estudiantes puedan estudiar otros conceptos físicos, susceptibles de ser reformulados cuánticamente, como lo son la difracción y el principio de incerteza. En esa dirección se está orientando nuestra investigación actual.

Referencias bibliográficas

BUNGUM, B. et al. ReleQuant – Improving teaching and learning in quantum physics through educational design research. Nordic Studies in Science Education. Oslo, v. 11, n. 2, pp. 153- 168. 2015.

CABRAL DE PAULO, I.; MOREIRA, M.A. Um estudo sobre a captação do significado do conceito de dualidade onda-partícula por alunos do ensino médio. Enseñanza de las Ciencias. Barcelona, n. extra, pp. 1-5. 2005.

CHEVALLARD, Y. La transposition didactique. Du savoir savant au savoir enseigne. La Pense´e Sauvage Edition. Grenoble: Francia. 1985.

CUPPARI, A. et al. Gradual introduction of some aspects of quantum mechanics in a high school curriculum. Physics Education. Londres, n. 32, pp. 302-308. 1997.

DOWRICK, N.J. Feynman’s sum-over-histories in elementary quantum mechanics. European Journal of Physics. Londres. n. 18, pp. 75-78. 1997.

FANARO, M.; OTERO, M.R. Basics Quantum Mechanics teaching in Secondary School: One Conceptual Structure based on Paths Integrals. Latin-American Journal of Physics Education, México, v. 2, n. 2, pp. 103-112. 2008.

FANARO, M.; OTERO, M.; ARLEGO, M. El método de caminos múltiples de Feynman para enseñar los conceptos fundamentales de la Mecánica Quántica en la escuela secundaria Caderno Brasileiro De Ensino De Física, Santa Catarina, v. 24, n. 2. pp. 233-260. 2007.

FANARO, M.; ARLEGO, M.; OTERO, M.R. Didactic Proposed for Teaching the Concepts of Electrons and Light in Secondary School Using Feynman ´s Path Sum Method. European Journal of Physics Education, Kayseri, v. 3. n. 2, pp. 1-11. 2012a.

FANARO, M.; ARLEGO, M.; OTERO, M.R. Teaching Basic Quantum Mechanics in Secondary School Using Concepts of Feynman’s Path Integrals Method. The Physics Teacher, College Park, v. 50, n. 3, pp. 156-158. 2012b.

FANARO, M.; ARLEGO, M.; OTERO, M.R. The double slit experience with light from Feynman´s Sum of Multiple Paths viewpoint Revista Brasileira De Ensino De Física, San Pablo, v. 36, n. 2, pp. 2308-1 a 2308-7. 2014.

FANARO, M.; ELGUE, M.; ARLEGO, M. Enseñanza por investigación en física en la escuela secundaria: aspectos básicos de mecánica cuántica en la ES. Edit. Universidad Nacional del Centro de la Provincia de Buenos Aires. Buenos Aires: Argentina. 2016.

FANARO, M.; ELGUE, M.; OTERO, M. Secuencia para enseñar conceptos acerca de la luz desde el enfoque de Feynman para la mecánica cuántica en la escuela secundaria: un análisis basado en la teoría de los campos conceptuales. Caderno Brasileiro de Ensino de Física, Santa Catarina, v. 33, n. 2, pp. 477-506. 2016.

FANARO, M. et al. Students' interpretation of quantum mechanics concepts from feynman´s sum of all paths applied to light. International Journal of Physics and Chemistry Education. Bremen. En prensa. 2017.

FANARO, M. et al.The problems secondary school students have being faced with the Feynman’s Sum of all Paths. In 2nd.WORLD CONFERENCE PHYSICS EDUCATION, San Pablo. pp.83-89. 2016c. Disponible en <http://www. livrosabertos.sibi.usp.br/portaldelivrosUSP/ catalog/view/177/162/771-1>. Visitado en: febrero 2018.

FEYNMAN, R. QED The strange theory of light and matter. Penguin Books. Princeton University Press. Princeton, Nueva Jersey: EE.UU. 1985.

FEYNMAN, R.; HIBBS A.R. Quantum Mechanics and Path Integrals Mc Graw Hills. New York: EEUU. 1965.

FISCHLER; H.; LICHTFELDT, M. Modern Phisycs and students’ conceptions. International Journal of Science Education. Londres v. 14, n. 2, pp. 181-190. 1992.

GONZÁLEZ, E.; FERNÁNDEZ, P.; SOLBES, J. Dificultades de docentes de ciencia en la conceptualización de temas de física actual. In: V SIMPOSIO DE INVESTIGACIÓN EN EDUCACIÓN EN FÍSICA. Memorias del V Simposio de Investigación en Educación en Física Tomo 1.138-147. Santa Fe. APFA.CD. 2000.

GRECA, I.; MOREIRA, M.A.; HERSCOVITZ, V. Uma Proposta para o Ensino de Mecânica Quântica. Revista Brasileira de Ensino de Física, San Pablo, v. 23, n. 4, pp. 444-457. 2001.

HADZIDAKI, P. Quantum Mechanics’ and ‘Scientific Explanation’ An Explanatory Strategy Aiming at providing ‘Understanding. Science & Education, v. 17, n. 1, pp. 49–73. 2008.

HANC, J.; TULEJA, S. The Feynman quantum mechanics with the help of Java applets and physlets in Slovakia. In 10TH WORKSHOP ON MULTIMEDIA IN PHYSICS TEACHING AND LEARNING. Berlin. Proccedings of 10TH WORKSHOP ON MULTIMEDIA IN PHYSICS TEACHING AND LEARNING. CD. 2005.

HENRIKSEN, E.K. et al. Relativity, quantum physics and philosophy in the upper secondary curriculum: challenges, opportunities and proposed approaches. Physics Education, Londres, v. 49, n. 6, pp. 678-684. 2014.

HENRIKSEN, E.K. et al. Improving teaching and learning in quantum physics through educational design research, Nordic Studies in Science Education. Oslo. v. 11, n. 2, pp. 153- 168. 2015.

HOBSON, A. Teaching Quantum Physics without paradoxes. The Physics Teacher, College Park, v. 45, pp. 96-99. 2007.

IRESON, G. The quantum understanding of pre-university physics students. Physics Education, Londres, v. 35, n. 1, pp. 15–21. 2000.

KRIJTENBURG-LEWERISSA, Pl, H.; BRINKMAN, A.; JOOLINGEN, V. Insights into teaching quantum mechanics in secondary and lower undergraduate education Physical review physics education research, Washington, v. 13, n. 1, pp. 010109-1 a 010109-21. 2017.

LOBATO, T.; GRECA, I. Analise da inserção de conteúdos de teoria quântica nos currículos de física do ensino médio. Ciência & Educação, Bauru, v. 11, n. 1, pp. 119-132. 2005.

MALGIERI, M.; ONORATO, P.; DE AMBROSIS, A. Teaching quantum physics by the sum over paths approach and GeoGebra simulations. European Journal of Physics, Londres, v. 35, n. 5. 2014.

MALGIERI, M.; ONORATO, P.; DE AMBROSIS, A. What is Light? From Optics to Quantum Physics Through the Sum over Paths Approach In TEACHING/ LEARNING PHYSICS INTEGRATING RESEARCH INTO PRACTICE GIREP-MPTL. Palermo. PROCEEDINGS OF THE GIREP MPTL CONFERENCE 2014, pp.639-646. 2015. Disponible en http://www1.unipa.it/girep2014/item6. html. Visitado en: agosto de 2017.

MANNILA, K.; KOPONEN, I.T.; NISKANEN, J.A. Building a picture of students’ conceptions of wave-and particle-like properties of quantum entities. European Journal of Physics, Londres, v. 23, n. 1, pp. 45–53. 2002.

MONTENEGRO, R.L.; PESSOA Jr., O. Interpretações da teoria quântica e as concepções dos alunos do curso de física. Investigações em Ensino de Ciências, Puerto Alegre, v. 7, n. 2, pp.107-122. 2002.

MOREIRA, M.A. ¿En qué sentido la teoría de los campos conceptuales puede ayudarnos para facilitar aprendizaje significativo? Investigações em Ensino de Ciências. Puerto Alegre. v. 12, n. 2, pp. 285-302. 2007.

MÜLLER, R.; WIESNER, H. Teaching quantum mechanics on an introductory level. American Journal of Physics, College Park, v. 70, n. 3, pp. 200-209. 2002.

NIEDDERER, H. Teaching quantum atomic physics in college and research results about a learning pathway. In INTERNATIONAL CONFERENCE ON UNDERGRADUATE PHYSICS EDUCATION (ICUPE) Proceedings of the International Conference on Undergraduate Physics Education. University of Maryland, College Park, EE.UU. 1996. Disponible en: <http://www.idn.uni-bremen.de/pubs/Niedderer/1996-ICUPE-HNTB.pdf>. Visitado en: agosto de 2017.

OGBORN, J.; HANC, J.; TAYLOR, E. Action on Stage: Historical Introduction. In The Girep Conference 2006: Modelling in Physics and Physics Education. Amsterdam. Proceedings GIREP Conference. pp. 213-219. 2006. Disponible en <https://www.iederkindeentalent.nl/wp-content/ uploads/2012/06/Girep-Proceedings-CD.pdf> Visitado en: agosto, 2017.

OLSEN, R.V. Introducing quantum mechanics in the upper secondary school: a study in Norway. International Journal of Science Education, Londres, v. 24, n. 6, pp. 565–574. 2002.

OSTERMAN, F.; MOREIRA, M. Uma revisão bibliográfica sobre a área de pesquisa Física moderna e contemporânea no ensino médio. Investigações em Ensino de Ciências. Puerto Alegre. v. 5, n. 1. 2000.

OSTERMAN, F.; RICCI, T. Construindo uma unidade didactica conceitual sobre mecanica cuantica: um estudo na formaçao de profesores de fisica. Ciencia & Educaçao, Bauru, v. 10, n. 2, pp. 235-257. 2004.

OTERO, M.R. Capítulo 1: La teoría de los Campos Conceptuales de Gerard Vergnaud. In: OTERO, M.R. et al. La teoría de los campos conceptuales y la conceptualización en el aula de matemática y física. Editorial Dunken. Buenos Aires, Argentina, pp. 15-32. 2014

PESSOA Jr., O. Interferometria, interpretação e intuição: uma introdução conceitual à Física Quântica. Revista Brasileira de Ensino de Física, San Pablo, v. 19, n. 1, pp. 27-47. 1997.

PINTO, A.C.; ZANETIC, J. É possível levar a Física Quântica para o Ensino Médio? Caderno Catarinense de Ensino de Física, Santa Catarina, v. 16, n. 1, pp. 7-34. 1999.

TAYLOR, F. et al. Teaching Feynman’s sum-over-paths quantum theory. Computers in Physics, Melville, v. 12, n. 2, pp. 190-199. 1998.

VERGNAUD, G. La teoría de los campos conceptuales. Recherches en Didáctique des Mathematiques, Grenoble, v. 10, n. 23, pp. 133-170. 1990.

VERGNAUD, G. (coord.). Aprendizajes y didácticas: ¿Qué hay de nuevo? Edicial. Buenos Aires: Argentina. 1994.

VERGNAUD, G. Pourquoi la théorie des champs conceptuels? Infancia y Aprendizaje, Somerville, v. 36, n. 2, pp. 131-161. 2013.

ZOLLMAN, D. Research on teaching and learning quantum mechanics. In ANNUAL MEETING NATIONAL ASSOCIATION FOR RESEARCH IN SCIENCE TEACHING (NARST). Reston. Papers presented at the annual meeting National Association for Research in Science Teaching National Science Foundation. 1999. Disponible en: <http://web.phys.ksu.edu/papers/narst/ QM_papers.pdf> Visitado en: agosto de 2017.