DOI:
https://doi.org/10.14483/udistrital.jour.gdla.2017.v12n1.a4Publicado:
2017-01-01A geometria nas aritméticas editadas para as escolas paroquiais luteranas do século xx no rio grande do sul, brasil
THE GEOMETRY ON ARITHMETICS EDITED FOR LUTHERAN PAROCHIAL SCHOOLS OF 20th CENTURY IN RIO GRANDE DO SUL, BRAZIL
Palabras clave:
History of Education, Mathematics, Geometry, Book (en).Palabras clave:
História da Educação, Matemática, Geometria, Livro (pt).Referencias
ARENDT, I. C. Educação, religião e identidade étnica: o Allgemeine Lehrerzeitung e a escola evangélica alemã no Rio Grande do Sul. São Leopoldo: Brasil, 2008.
ARENDT, I. C. Representações de Germanidade, Escola e Professor no Allgemeine Lehrerzeitung für Rio Grande do Sul [Jornal Geral para o Professor no Rio Grande do Sul]. 292 pp. Tese de Doutorado em História, Universidade do Vale do Rio dos Sinos, São Leopoldo: Brasil, 2005.
CHARTIER, R. A História Cultural: entre práticas e representações. Lisboa: Portugal, 1990.
CHERVEL, A. História das disciplinas escolares – reflexões sobre um campo de pesquisa. Teoria & Educação, Porto Alegre, n. 2, p. 177-229, 1990.
GOERL, O. A. Série Concórdia: Primeira Aritmética. Porto Alegre: Brasil, [194-a].
GOERL, O. A. Série Concórdia: Segunda Aritmética. Porto Alegre: Brasil, [194-b].
JULIA, D. A cultura escolar como objeto histórico. Revista Brasileira de História da Educação, Campinas, n. 1, p. 9-43, jan./jun. 2001.
KNIJNIK, G. Exclusão e resistência: educação matemática e legitimidade cultural. Porto Alegre: Brasil, 1996.
KREUTZ, L. Livros escolares e imprensa educacional periódica dos imigrantes alemães no Rio Grande do Sul, Brasil 1870-1939. Revista Educação em Questão, Natal, v. 31, n. 17, p. 24-52, jan./abr. 2008.
KREUTZ, L. Material didático e currículo na escola teuto-brasileira. São Leopoldo: Brasil, 1994.
KREUTZ, L. O professor paroquial: magistério e imigração alemã. Porto Alegre: Brasil, 1991.
KREUTZ, L.; ARENDT, I. C. (Org.). Livros escolares das escolas de imigração alemã no Brasil (1832-1940). Acervo documental e de pesquisa. São Leopoldo: Brasil, 2007. 3 CD-ROM.
KUHN, M. C.O ensino da Matemática nas escolas evangélicas luteranas do Rio Grande do Sul durante a primeira metade do século XX. 466 pp. Tese de Doutorado em Ensino de Ciências e Matemática – Universidade Luterana do Brasil, Canoas, 2015.
LEMKE, M. D. Os princípios da educação cristã luterana e a gestão de escolas confessionárias no contexto das ideias pedagógicas no sul do Brasil (1824 – 1997). Canoas: Brasil, 2001.
MAURO, S. Uma história da matemática escolar desenvolvida por comunidades de origem alemã no Rio Grande do Sul no final do século XIX e início do século XX. 257 pp. Tese de Doutorado em Educação Matemática – Universidade Estadual Paulista, Rio Claro, 2005.
PROST, A. Doze lições sobre a História. Belo Horizonte, Autêntica, 2008.
RAMBO, A. B. A escola comunitária teuto-brasileira católica. São Leopoldo: Brasil, 1994.
RAMBO, A. B.A escola comunitária teuto-brasileira católica: a associação de professores e a escola normal. São Leopoldo: Brasil, 1996.
ROCHE, J. A Colonização Alemã e o Rio Grande do Sul. Porto Alegre: Brasil, 1969. v. 1 e v. 2.
SÉRIE Concórdia: Segunda Aritmética. Porto Alegre: Brasil, 1948.
SÉRIE Concórdia: Terceira Aritmética. Porto Alegre: Brasil, 1949.
SÉRIE Ordem e Progresso: Terceira Arithmetica. Porto Alegre: Brasil, [193-].
STRELOW, F. Série Ordem e Progresso: Primeira Aritmética. Porto Alegre: Brasil, [193-].
UNSERE SCHULE. Porto Alegre: Brasil, 1933-1935.
VALENTE, W. R. História da Educação Matemática: interrogações metodológicas. REVEMAT – Revista Eletrônica de Educação Matemática, UFSC, v. 2.2, p. 28-49, 2007.
VALENTE, W. R.; PINHEIRO, N. V. L. Chega de decorar a tabuada! – As cartas de Parker e a árvore do cálculo na ruptura de uma tradição. Educação Matemática em Revista - RS, Canoas, v. 1, n. 16, p. 22-37, 2015.
WANDERER, F. Escola e Matemática Escolar: mecanismos de regulação sobre sujeitos escolares de uma localidade rural de colonização alemã no Rio Grande do Sul. 228 pp. Tese de Doutorado em Educação – Universidade do Vale do Rio dos Sinos, São Leopoldo, 2007.
WARTH, C. H. Crônicas da Igreja: Fatos Históricos da Igreja Evangélica Luterana do Brasil (1900 a 1974). Porto Alegre: Brasil, 1979.
Cómo citar
APA
ACM
ACS
ABNT
Chicago
Harvard
IEEE
MLA
Turabian
Vancouver
Descargar cita
DOI: 10.14483/udistrital.jour.gdla.2017.v12n1.a4
A GEOMETRIA NAS ARITMÉTICAS EDITADAS PARA AS ESCOLAS PAROQUIAIS LUTERANAS DO SÉCULO XX NO RIO GRANDE DO SUL, BRASIL
The geometry in the arithmetic edited for the lutheran parochial schools of the 20th century in Rio Grande do Sul, Brazil
Malcus Cassiano Kuhn1
Arno Bayer2
Para citar como este artículo: Kuhn, M.C., Bayer, A. (2017). A geometria nas aritméticas editadas para as escolas paroquiais luteranas do século XX no Rio Grande do Sul, Brasil. Góndola, Enseñ Aprend Cienc, 12(1), 57-72. doi: 10.14483/udistrital.jour.gdla.2017.v12n1.a4.
Recibido: 17 de junio 2016 / Aceptado: 21 de noviembre de 2016
1 Pós-doutorando do Programa de Pós-graduação em Ensino de Ciências e Matemática da Universidade Luterana do Brasil – ULBRA/Canoas/ RS/Brasil. Professor do Instituto Federal de Educação, Ciência e Tecnologia Sul-rio-grandense – IFSul Câmpus Lajeado/RS/Brasil. Correio eletrônico: malcuskuhn@ifsul.edu.br
2 Doutor em Ciências da Educação pela Universidade de Salamanca - Espanha. Professor e pesquisador do Programa de Pós-graduação em Ensino de Ciências e Matemática da Universidade Luterana do Brasil – ULBRA/Canoas/RS/Brasil. Correio eletrônico bayer@ulbra.br
Resumo
O artigo discute a geometria nas aritméticas da série Ordem e Progresso e da série Concórdia, editadas pela Igreja Evangélica Luterana do Brasil para suas escolas paroquiais do século XX, no Rio Grande do Sul. O Sínodo de Missouri, hoje Igreja Evangélica Luterana do Brasil, iniciou missão nas colônias alemãs gaúchas em 1900, fundando congregações religiosas e escolas paroquiais. Estas escolas estavam inseridas num projeto missionário e comunitário que buscava ensinar a língua materna, matemática, valores culturais, sociais e, principalmente, religiosos. Fundamentando-se na história cultural, verificou-se que os conhecimentos geométricos foram relacionados com formas geométricas, desenhos em escala, medidas de comprimento, medidas de superfície, medidas de volume e com as antigas medidas brasileiras. Os autores das aritméticas usaram a estratégia de apresentar propostas de ensino da geometria de forma prática e associada com situações reais para que os alunos das escolas paroquiais luteranas gaúchas se apropriassem desses conhecimentos matemáticos, e no futuro, realizassem a administração correta do seu orçamento familiar e o gerenciamento da sua propriedade rural.
Palavras chaves:: história da educação, matemática, geometria, livro.
Abstract
We discuss the geometry on arithmetic into the series “Order and Progress” and “Concordia”, edited by Evangelical Lutheran Church of Brazil to their parochial schools of the 20th century, in Rio Grande do Sul. The Missouri Synod, currently Evangelical Lutheran Church of Brazil, began mission in gaucho-german colonies in 1900, founding religious congregations and parochial schools. These schools were inserted in a missionary and community project that sought to teach the mother tongue, mathematics, cultural, social, and mainly, religious values. It has been found that geometric knowledge were related to geometric shapes, scale drawings, length measures, surface measures, volume measures and the old Brazilian measures. Authors of arithmetic had as strategy presenting teaching proposals of the geometry in a practical way and associated with real situations, so that students of gaucho-lutheran parochial schools appropriating these mathematical knowledge, and in the future, they could make correct administration of their family budget and could manage their rural property.
Keywords: history of Education, mathematics, geometry, book.
Introdução
Este artigo tem por objetivo discutir a geometria nas aritméticas da série Ordem e Progresso e da série Concórdia, editadas pela Igreja Evangélica Luterana do Brasil (IELB) para suas escolas paroquiais do século XX, no Rio Grande do Sul-RS, Brasil. Trata-se de um estudo iniciado durante a elaboração da tese sobre “o ensino da Matemática nas Escolas Evangélicas Luteranas do Rio Grande do Sul durante a primeira metade do século XX” e aprofundado durante o estágio Pós-doutoral, junto ao Programa de Pós-Graduação em Ensino de Ciências e Matemática (PPGECIM) da Universidade Luterana do Brasil (ULBRA), do município de Canoas, RS, Brasil.
O movimento migratório no RS tem sido objeto de muitas investigações. No âmbito da História da Educação no RS, os trabalhos de KREUTZ (1991, 1994, 2008), RAMBO (1994, 1996), LEMKE (2001), ARENDT (2005, 2008) e WEIDUSCHADT (2007, 2012) são destaques. Na História da Educação Matemática no RS, destacam-se as pesquisas de MAURO (2005), KREUTZ e ARENDT (2007), WANDERER (2007) e KUHN (2015).
De acordo com PROST (2008), os fatos históricos são constituídos a partir de traços deixados no presente pelo passado. Assim, a tarefa do historiador consiste em efetuar um trabalho sobre esses traços para construir os fatos. Como a temática investigada se insere na História da Educação Matemática no RS, busca-se na história cultural (Kulturgeschichte) o suporte para discussão. A história cultural estuda os elementos das relações familiares, tradições, costumes, representações, práticas, ideias, língua, religião, etc. “Tem por principal objeto, identificar o modo como em diferentes lugares e momentos uma determinada realidade social é construída, pensada, dada a ler” (CHARTIER, 1990, pp. 16).
Acrescenta que uma questão desafiadora para a história cultural é o uso que as pessoas fazem dos objetos que lhes são distribuídos ou dos modelos que lhes são impostos, uma vez que há sempre uma prática diferenciada na apropriação dos objetos colocados em circulação. Na perspectiva de CHARTIER (1990), pode-se dizer que a imprensa pedagógica, aqui representada pelas aritméticas da série Ordem e Progresso e da série Concórdia, foi um veículo para circulação de ideias que traduzem valores e comportamentos que se deseja ensinar – a doutrina luterana, sendo postas em convergência com outras estratégias políticas e culturais no estado gaúcho.
CHERVEL (1990) considera importante o estudo histórico da cultura escolar para a compreensão dos elementos que participam da produção/elaboração/ constituição dos saberes escolares e, em particular, da matemática escolar e sua história. JULIA (2001) define a cultura escolar como um conjunto de normas que estabelecem conhecimentos a ensinar e condutas a inspirar, e um conjunto de práticas que permitem a transmissão desses conhecimentos e a incorporação desses comportamentos. De acordo com VALENTE (2007), pensar os saberes escolares como elementos da cultura escolar, realizar o estudo histórico da matemática escolar, exige que se devam considerar os produtos dessa cultura do ensino de matemática, que deixaram traços que permitem o seu estudo, como as aritméticas da série Ordem e Progresso e da série Concórdia, principais fontes documentais desta investigação.
Precedendo a discussão da geometria nas aritméticas da série Ordem e Progresso e da série Concórdia, apresenta-se uma breve caracterização das escolas paroquiais luteranas gaúchas do século passado.
As escolas paroquiais luteranas gaúchas do século XX
Conforme estudos realizados por KUHN (2015), a imigração alemã para o RS, a partir de 1824, contribuiu significativamente para o desenvolvimento do estado através da colonização de regiões cobertas por florestas e ainda não exploradas. Os primeiros anos dessa colonização foram marcados pela luta por sobrevivência em meio ao desbravamento das matas, enfrentando-se as mais diversas adversidades. Aos poucos, a estrutura da picada, linha ou comunidade foi se constituindo com as casas e as benfeitorias dos colonos, a igreja (católica/evangélica), a escola, a casa do professor/ padre/pastor, o cemitério, o salão de festas e a casa comercial. Assim, os principais eixos institucionais da picada estavam constituídos: religião, escola, agricultura, arte e diversões.
Através dos primeiros imigrantes alemães, os princípios cristãos de Lutero também começaram a se fazer presentes no Brasil. Lutero traçou princípios gerais sobre a educação, os quais se fundamentaram na Bíblia. “A premissa fundamental é de que a Bíblia ensina que Deus criou o universo e mantém, governa e sustenta toda a criação, sendo o homem a obra máxima da criação” (LEMKE, 2001, pp. 34).
Nesta perspectiva luterana, o Sínodo Evangélico Luterano Alemão de Missouri3, hoje IELB, começou sua missão nas colônias alemãs do RS, em 1900, fundando congregações religiosas e escolas paroquiais. Para o Sínodo de Missouri era necessário consolidar um campo religioso e fortalecê-lo investindo na escola, influenciando o campo familiar dos seus possíveis fiéis. “A escola paroquial se revelou como uma grande benção para o bem e o desenvolvimento da Igreja Luterana. As congregações que mantinham escolas paroquiais, geralmente eram as melhores congregações” (WARTH, 1979, pp. 195). Por isso, os missourianos não somente cuidaram da formação de pastores como também de professores que atuassem de acordo com a filosofia educacional missouriana, para que as escolas paroquiais atingissem seus objetivos como agência missionária e de educação geral.
3 Em 1847, um grupo de imigrantes luteranos alemães da Saxônia fundou no estado de Missouri (EUA), o Sínodo Evangélico Luterano Alemão de Missouri, Ohio e Outros Estados, atualmente Igreja Luterana - Sínodo de Missouri (WARTH, 1979)
Os egressos das escolas paroquiais luteranas gaúchas tinham amplo conhecimento da Bíblia e uma formação consistente de crenças e valores cristãos tradicionais que enfatizavam a importância do relacionamento com Deus e com outras pessoas. Tinha-se a preocupação pedagógica para que a espiritualidade fosse vivida no dia a dia e não se reduzisse a ritos religiosos. Os pais buscavam uma escola paroquial, pois tinham pouco tempo e capacidade para eles mesmos proporcionarem a seus filhos os devidos ensinamentos.
Numa escola paroquial, o professor, além das matérias seculares, exigidas pelas leis do Estado, antes de tudo, ensinava a religião. O ensino diário de todas as matérias e de toda a educação deveria estar sob a influência da Palavra de Deus. Numa escola cristã reinava um espírito cristão, e os alunos não estavam em perigo de aprender coisas que não condiziam com a Palavra de Deus e a disciplina cristã. (WARTH, 1979, pp. 195
De acordo com KUHN (2015), as escolas paroquiais luteranas estavam inseridas num projeto missionário e comunitário que buscava ensinar a língua materna, a matemática, valores culturais, sociais e, principalmente, religiosos. Tinham uma responsabilidade para com a comunidade no sentido de junto e com ela, promover o crescimento e o desenvolvimento pessoal de todos que a compõe, focando a cidadania. Se a escola formasse o ser humano com postura ética e moral exemplar, este poderia promover transformações sólidas em seu contexto social e seria um verdadeiro colaborador na seara de Deus e para o governo do mundo. As escolas paroquiais luteranas gaúchas foram assim caracterizadas por WEIDUSCHADT (2007):
As escolas eram organizadas de forma multisseriada. As turmas eram compostas de 20 a 40 alunos. Na maioria das vezes, o pastor da comunidade era, ao mesmo tempo, professor. A comunidade sustentava a estrutura física e mantinham o professor da escola. O prédio era muitas vezes o mesmo local do templo. A ligação entre a escola e a igreja era importante, porque logo no início da formação das comunidades o ensino doutrinário e pedagógico era ressaltado e sua suplementação implicava questões econômicas e culturais para a implementação. O projeto escolar dentro da comunidade religiosa era marcante, a orientação e a obrigação de os pais enviarem os filhos à escola eram quase obrigatórias, com sanções econômicas e morais, caso não concordassem. (WEIDUSCHADT, 2007, pp. 166-168)
O ensino da matemática nas escolas paroquiais luteranas gaúchas do século XX
De acordo com KUHN (2015), o ensino da matemática, nos primeiros anos de escolarização nas escolas paroquiais luteranas gaúchas do século passado, priorizava os números naturais, os sistemas de medidas, as frações ordinárias e decimais, complementando-se com a matemática comercial e financeira e a geometria. O ensino da matemática deveria acontecer de forma prática e articulada com as necessidades dos futuros agricultores, observando-se a doutrina luterana.
Conforme KREUTZ (1994), o currículo das escolas estava organizado de forma que as crianças aprendessem o essencial para o bom entrosamento na vida das comunidades rurais, tanto sob o aspecto religioso e social quanto do trabalho. Havia preocupação em se construir o conhecimento vinculado à realidade do aluno. O autor complementa que a prioridade eram as operações básicas que pudessem ser feitas mentalmente, nas circunstâncias concretas da vida agrária, seja na forma, como no conteúdo. Por isso, dava-se ênfase aos Kopfrechnungen (cálculos feitos mentalmente), já que na vida agrícola a pessoa teria que calcular, com frequência, sem ter o papel e lápis à mão. O próprio título de um dos manuais usados nesta disciplina, o Praktische Rechenschule (o ensino prático da matemática), de Otto Büchler , reflete este entendimento. Ressalta-se que até mais ou menos 1932, predominava o ensino tradicional no Brasil. De 1932 até 1960, os alunos sofreram as influências do evolucionismo e do pragmatismo, período denominado de Escola Nova.
O ensino da matemática nas escolas paroquiais luteranas gaúchas do século XX
De acordo com KUHN (2015), o ensino da matemática, nos primeiros anos de escolarização nas escolas paroquiais luteranas gaúchas do século passado, priorizava os números naturais, os sistemas de medidas, as frações ordinárias e decimais, complementando-se com a matemática comercial e financeira e a geometria. O ensino da matemática deveria acontecer de forma prática e articulada com as necessidades dos futuros agricultores, observando-se a doutrina luterana.
Conforme KREUTZ (1994), o currículo das escolas estava organizado de forma que as crianças aprendessem o essencial para o bom entrosamento na vida das comunidades rurais, tanto sob o aspecto religioso e social quanto do trabalho. Havia preocupação em se construir o conhecimento vinculado à realidade do aluno. O autor complementa que a prioridade eram as operações básicas que pudessem ser feitas mentalmente, nas circunstâncias concretas da vida agrária, seja na forma, como no conteúdo. Por isso, dava-se ênfase aos Kopfrechnungen (cálculos feitos mentalmente), já que na vida agrícola a pessoa teria que calcular, com frequência, sem ter o papel e lápis à mão. O próprio título de um dos manuais usados nesta disciplina, o Praktische Rechenschule (o ensino prático da matemática), de Otto Büchler4, reflete este entendimento. Ressalta-se que até mais ou menos 1932, predominava o ensino tradicional no Brasil. De 1932 até 1960, os alunos sofreram as influências do evolucionismo e do pragmatismo, período denominado de Escola Nova.
Com relação ao ensino da geometria nas escolas paroquiais, RAMBO (1994) escreve que:
O colono tinha que saber fazer previsões confiáveis para correta administração do orçamento familiar e o gerenciamento da produção da sua propriedade rural. Lidando com a terra, era obrigado a fazer cálculos aproximados de superfície. Esse fato obrigava a assimilar noções básicas de geometria, além de conhecimentos corretos do sistema métrico. [...] O trabalho com madeira, com grãos, com banha só podia ser confiável com o domínio dos rudimentos do cálculo volumétrico nas suas mais diversas formas. (RAMBO, 1994, pp. 154-155)
Os primeiros trinta anos de existência das escolas paroquiais luteranas gaúchas foram marcados pela carência de materiais didáticos e pela progressiva adoção dos quatro manuais de Büchler, tanto em alemão, quanto em português, para as aulas de matemática. No periódico Unsere Schule5 (AGO, 1933, pp. 6, tradução nossa), afirma-se que “os livros de aritmética de Büchler (editora Rotermund)6 são usados na maioria das escolas paroquiais luteranas e que a mesma editora lançou recentemente um novo manual: meu livro de contas, por W. Nast e L. Tochtrop”. Porém, na mesma edição, este manual é analisado criticamente, apontando-se a necessidade de uma edição com princípios morais e educacionais luteranos, com uso de princípios pedagógicos modernos e adaptada às condições nacionais, pois o processo de nacionalização do ensino7 estava em curso.
Por isso, o Sínodo de Missouri começou a produzir seus próprios livros de aritmética na década de 1930. A Casa Publicadora Concórdia8 , de Porto Alegre, editou e publicou o material didático específico para as escolas paroquiais luteranas. Para as aulas de matemática, foram publicadas duas séries: a série Ordem e Progresso, lançada na década de 1930, pela divulgação feita no periódico Unsere Schule, e a série Concórdia, lançada na década de 1940. De acordo com LEMKE (2001, pp. 79), “a série Ordem e Progresso é uma coleção constituída por livros de leitura, história bíblica e matemática em que os próprios textos de alfabetização e cálculotrazem ensinamentos bíblicos e contém temas decunho moral e cristão”.
4 Otto Büchler foi autor de livros de aritmética utilizados nas escolas teuto-brasileiras do século XX.
5 Na década de 1930, a IELB começou a publicar um periódico pedagógico dirigido às escolas paroquiais luteranas, chamado Unsere Schule (Nossa Escola), predominando informações e artigos pedagógicos escritos em alemão.
6 A editora Rotermund, de São Leopoldo, editava e publicava o material didático relacionado ao Sínodo Rio-Grandense (Igreja Evangélica de Confissão Luterana no Brasil – IECLB).
7 Uma série de decretos dos governos estadual e federal, emitidos principalmente no final da década de 1930, disciplinaram a licença de professores e o material didático a ser usado nas escolas, tornaram o idioma nacional obrigatório (português) para a instrução e prescreveram a intensificação da formação cívica brasileira.
8 Fundada em 1923, fazia a edição de livros e de periódicos relacionados à literatura religiosa e escolar da IELB. Foi a primeira e a única redatora da IELB, existente até os dias atuais. Antes de sua fundação, os livros e os periódicos eram impressos pela Concordia Publishing House, nos Estados Unidos, e enviados ao Brasil.
A série Ordem e Progresso e a série Concórdia contém três aritméticas voltadas para o ensino da matemática nos primeiros anos de escolarização. No Instituto Histórico da IELB, em Porto Alegre, localizaram-se a Primeira e a Terceira Arithmetica da série Ordem e Progresso, além de uma edição da Primeira Aritmética, duas edições da Segunda Aritmética e uma edição da Terceira Aritmética da série Concórdia. Ainda não foi localizada a Segunda Aritmética da série Ordem e Progresso.
A investigação da geometria nas aritméticas da série Ordem e Progresso e da série Concórdia, brevemente apresentadas no Quadro 1, fundamenta-se no referencial teórico-metodológico da história cultural.
A partir do Quadro 1 se verifica que somente três aritméticas possuem autoria declarada, porém, acredita-se que os autores das demais obras também tenham sido professores das escolas paroquiais luteranas, pois o periódico Unsere Schule se refere à edição de livros de aritmética da seguinte maneira: “o Sínodo decidiu que será editado um trabalho completo de aritmética. Os professores Frederico Strelow, Albert Brückmann e Max Öhlwein foram contratados para realizar o trabalho” (UNSERE SCHULE, mar./abr. 1934, p. 14, tradução nossa). Observa-se ainda que o número de páginas de cada livro aumenta conforme o nível de escolarização primária e que as duas edições da Terceira Aritmética têm o mesmo número de páginas (143), abordam as mesmas unidades de estudo e exercícios, com a mesma distribuição de páginas para cada conteúdo no livro, havendo apenas variações na ortografia de palavras e na representação de unidades de medida e do sistema monetário. Não se pode informar a quantidade de exemplares publicados de cada edição, pois esta informação não foi encontrada. Ressalta-se que as aritméticas da série Ordem e Progresso e da série Concórdia foram editadas com base em princípios morais e educacionais idealizados pela IELB.
A geometria nas aritméticas da série Ordem e Progresso e da série Concórdia
Na análise das duas aritméticas da série Ordem e Progresso e das quatro aritméticas da série Concórdia, a partir do referencial teórico-metodológico desta investigação, constatou-se que essas obras enfatizam conhecimentos matemáticos relacionados com a aritmética, identificando-se algumas propostas de estudo, envolvendo a geometria, somente nas edições da Segunda e Terceira Aritmética.
Quadro 1. Aritméticas analisadas.
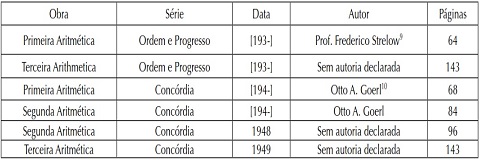
Fonte.Série Ordem e Progresso e série Concórdia.
9 Frederico Strelow (1888-1946) se formou na primeira turma de professores no Seminário Concórdia - Instituto pedagógico-teológico que atuou na formação de pastores e de professores paroquiais para IELB -, em abril de 1912. Foi professor paroquial, redator do periódico pedagógico Unsere Schule e autor da Primeira Aritmética da série Ordem e Progresso.
10 O gaúcho Otto Adolpho Goerl (1905-1998) também se formou no Seminário Concórdia, em 1925, e foi ordenado pastor em 1926. Além de pastor, foi professor paroquial e, posteriormente, professor e diretor do Seminário Concórdia. Autor de livros para o ensino da aritmética e leitura nas escolas paroquiais luteranas.
A edição da Primeira Aritmética da série Ordem e Progresso enfatiza o estudo da numeração até 100. O estudo dos números de 0 a 100 inicia com a numeração de 0 a 10, explorando o significado de quantidades até 10 e as operações de adição e subtração. Depois, amplia-se o estudo com os números até 100, envolvendo a escrita em ordem crescente e decrescente dos números e as operações de adição, subtração, multiplicação e divisão. Destaca-se a existência de inúmeras propostas de cálculos orais e cálculos por escrito com o algoritmo na horizontal, envolvendo as quatro operações com números naturais até 100. Na introdução dos números até 10 se observa que o autor emprega o método de ensino intuitivo, mas no restante da obra predominam propostas de ensino marcadas pela retórica e memorização.
A Primeira Aritmética da série Concórdia está dividida em quatro secções: I – Números de 1 a 5, com foco em contar e desenhar, escrever os números, somar e diminuir; II – Números de 1 a 10, com atenção para o significado dos números até 10 e as operações de adição e subtração; III – Números de 1 a 20, ênfase nas operações de adição e subtração; IV – Números de 1 a 100, explorando as dezenas, dezenas e unidades, as operações de adição, subtração, multiplicação e divisão, e a pequena tabuada. O autor desta aritmética dá maior ênfase para o método intuitivo em suas propostas de ensino, mas também traz atividades que enfatizam a tradição pedagógica da memorização (VALENTE, PINHEIRO, 2015).
A Segunda Aritmética da série Concórdia, de Goerl, O. [194-b], está dividida em três secções: I – Números de 1 a 100 (recapitulação), com as operações de adição, subtração, multiplicação e divisão; II – Números de 1 a 1000, relacionando unidades, dezenas e centenas, bem como as operações de adição, subtração, multiplicação e divisão; III – Números até 10000, explorando as classes de milhares, centenas, dezenas e unidades, números pares e ímpares, operações de adição, subtração, multiplicação e divisão. Mesmo que o autor desta aritmética proponha a resolução de problemas contextualizados com a realidade dos alunos das escolas paroquiais luteranas gaúchas, observaram-se várias propostas de ensino para o desenvolvimento de habilidades para o cálculo mental e escrito. Nesta aritmética se encontrou uma proposta de ensino relacionada com a geometria, na qual se propõe fazer medidas usando uma régua, conforme descrito no Quadro 2:
Quadro 2. Vamos medir!

Fonte. Goerl, O. [194-b], p. 34.
As atividades desta Segunda Aritmética, descritas no Quadro 2, têm o propósito de trabalhar com medidas de comprimento de forma concreta, ao proporem a medição de dimensões de objetos, da escola e do pátio. Verifica-se que são exploradas as três dimensões: comprimento, largura e altura. Nestas atividades fica subentendida a transformação de centímetros para metros, especialmente nos exercícios 3 e 4, para melhor representar as dimensões medidas.
Na página seguinte da mesma aritmética, são propostas outras atividades envolvendo medidas de forma concreta, conforme apresentado no Quadro 3:
Quadro 3. Problemas sobre medidas.

Fonte. Goerl, O. [194-b], p. 35.
Nas atividades descritas no Quadro 3, o autor também propõe a realização de medidas de objetos da sala de aula e de dimensões da escola, associadas a situações que exigem a realização de cálculos de adição ou subtração, envolvendo unidades de medida de comprimento. Observa-se que o exercício 4 sugere a representação geométrica para resolução.
Constatou-se que a edição da Segunda Aritmética de Goerl, O. [194-b] traz apenas os conhecimentos geométricos relacionados nos quadros 2 e 3, numa proposta de estudo que instrumentaliza os alunos para realização de medidas de comprimento de forma prática e contextualizada, evidenciando-se o emprego do método de ensino intuitivo.
A edição da Segunda Aritmética, editada em 1948, traz como principais unidades de estudo: numeração 1 - 1000; os números até 10000; números além de 10000. Para o estudo dos números até 1000, propõem-se três seções: I – contar, escrever e ler os números: centenas; centenas e dezenas; centenas, dezenas, unidades; II – somar e diminuir: somar e diminuir as unidades; somar e diminuir números de dois algarismos; somar e diminuir números de três algarismos; III – multiplicar e dividir. No estudo dos números até 10000, o livro propõe um roteiro semelhante ao anterior: I – contar, escrever e ler os números; II – somar e diminuir; III – multiplicar e dividir. Para o estudo dos números além de 10000, a proposta da obra começa com a leitura e escrita de números, seguida das operações de multiplicação e divisão. Nesta aritmética predominam propostas de ensino para o desenvolvimento de habilidades para o cálculo mental e escrito. Verificou-se que, nesta edição, o ensino da geometria é explorado através de atividades com desenhos em escala, estudo do metro quadrado e de unidades de medida de superfícies. Na Figura 1 se apresentam exercícios com desenhos em escala:
Figura 1. Desenhando em escala.
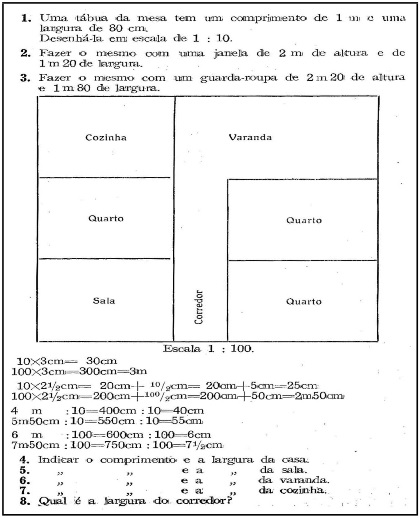
Fonte. Série Concórdia, 1948, p. 80.
O excerto, apresentado na Figura 1, explora os desenhos em escala, articulando a geometria com a proporção. Partindo de medidas reais de uma tábua, uma janela e um armário propõe-se o desenho numa escala de 1:10. Observa-se o desenho dos cômodos de uma casa numa escala de 1:100, uma sistematização com medidas lineares envolvendo multiplicações e divisões por 10 e 100 e cinco exercícios relacionados ao desenho em escala para determinação das dimensões reais da casa e seus cômodos. Observa-se que falta clareza na exposição das medidas de cada peça da casa, podendo comprometer a resolução dos exercícios propostos. Esta aritmética ainda propõe dois exercícios práticos envolvendo desenhos em escala: “9) Tomar medida da nossa aula e desenhá-la em escala de 1:10 no quadro negro. Em escala de 1:100 no caderno. 10) Tomar medida do pátio e desenhá-lo em escala de 1:100 no quadro preto” (SÉRIE CONCÓRDIA, 1948, pp. 81). Embora a proposta de estudo faça uso da representação de proporção (escala de a:b), parece que a intenção é aplicar a operação de divisão por 10 e 100 na representação geométrica de objetos reais (redução) e a operação de multiplicação por 10 e 100 na determinação de medidas reais de objetos desenhados em escala (ampliação), ficando subentendida a relação da geometria com a proporção nesta proposta de ensino.
Na Figura 2 se apresenta a proposta de estudo para o metro quadrado, encontrada nesta edição da Segunda Aritmética:
Figura 2. O metro quadrado
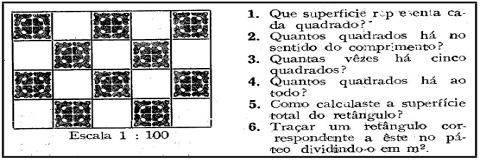
Fonte. Série Concórdia, 1948, p. 87.
Para que o aluno possa responder que superfície representa cada quadrado do exercício 1, mostrado na Figura 2, precisa utilizar os conhecimentos desenvolvidos sobre escalas de medidas, pois o desenho está representado na escala 1:100. Observa-se que os exercícios 2, 3, 4 e 5 estão propostos para a determinação da superfície do retângulo de forma intuitiva. O exercício 6 propõe a construção de um retângulo no pátio da escola, explorando a ideia de metro quadrado de forma prática. Esta construção dos conhecimentos geométricos era importante, pois os futuros colonos tinham que assimilar noções básicas de geometria na escola, além de conhecimentos do sistema métrico, para gerenciar corretamente sua propriedade rural (KUHN, 2015).
No Quadro 4 se apresentam problemas propostos na Segunda de Aritmética de 1948 e relacionados com conhecimentos geométricos:
Quadro 4. Problemas sobre geometria.

Fonte. Série Concórdia, 1948, p. 87.
Os problemas, descritos no Quadro 4, exploram áreas de superfícies retangulares de forma contextualizada e articulada com operações comerciais. Ressalta-se que o artesanato rural, surgido nas regiões de colonização alemã do RS, dividiu-se em dois ramos: “o fornecimento de artigos e serviços necessários à vida local e a transformação dos produtos agrícolas para torná-los exportáveis. Destacaram-se ferreiros, serralheiros, funileiros, pedreiros, marceneiros, alfaiates, sapateiros, curtumes, moinhos de farinha, alambiques” (ROCHE, 1969, pp. 482). Esta proposta de estudo evidencia a preocupação dos editores em empregar situações reais para que os alunos se apropriassem dos conhecimentos matemáticos (CHARTIER, 1990).
A mesma aritmética, ainda, explora unidades de medida de superfícies, conforme observado no Quadro 5:
Quadro 5. Unidades de medida de superfícies.

Fonte. Série Concórdia, 1948, p. 87.
As unidades de medida de superfície: are, hectare (ha), braça quadrada e quadra quadrada, apresentadas no Quadro 5, estão relacionadas com o metro quadrado (m²):
1 are = 100 m².
1 ha = 10000 m² = 100 ares.
1 braça quadrada = 2 m 20 x 2 m 20 = 4,84 m².
1 quadra quadrada = 132 m x 132 m = 17424 m².
A unidade palmo quadrado está relacionada com centímetros quadrados (cm²), ou seja, 1 palmo quadrado = 22 cm x 22 cm = 484 cm² = 0,0484 m². Estas unidades de medida de superfície são antigas medidas de superfície brasileiras, utilizadas pelos colonos em regiões agrícolas, principalmente para medidas de área de terras. Acrescenta-se que a unidade de medida hectare (ha) ainda é utilizada com frequência na referência a superfícies de terras cultiváveis. Ressalta-se que as atividades apresentadas no final do Quadro 5 exploram a representação concreta das unidades de superfície: metro quadrado, braça quadrada e are, no pátio da escola, empregando-se o método de ensino intuitivo e favorecendo a compreensão dessas medidas de superfície.
As principais unidades de estudo das edições da Terceira Aritmética são: frações decimais e sistema métrico; frações ordinárias; regra de três; porcentagem; porcentagem comercial; juros; razão e proporção; geometria prática. Estas aritméticas são caracterizadas por apresentarem propostas de estudo mais sistematizadas dos conhecimentos matemáticos.
Os primeiros registros de conhecimentos geométricos encontrados nas edições da Terceira Aritmética estão relacionados com as unidades de medida de comprimento, superfície, volume e com as antigas medidas brasileiras. De acordo com a Terceira Arithmetica da série Ordem e Progresso ([193-], pp. 16), “a unidade principal das medidas de superfície é o metro quadrado (m²). O metro quadrado é um quadrado que tem 1 m de cada lado”. Com relação às medidas de volume, na Terceira Aritmética da série Concórdia (1949, pp. 22), encontra-se que “a unidade principal é o metro cúbico (m³). O metro cúbico é um cubo cujas faces são metros quadrados, ou um cubo que tem um metro de aresta”. A partir destas definições e das relações entre as unidades de medida de comprimento, superfície e volume, propõe-se a resolução de problemas envolvendo formas geométricas, conforme descrito no Quadro 6:
Quadro 6. Problemas sobre perímetro e volume

Fonte. Série Concórdia, 1949.
Os dois primeiros problemas, apresentados no Quadro 6, estão relacionados com a forma geométrica retangular, em contextos semelhantes, e exploram relações entre as unidades de medida de comprimento. No primeiro problema, dadas as dimensões de um potreiro retangular e a quantidade de moirões existentes em seu perímetro, é preciso determinar a distância entre os moirões. No segundo problema, apresentam-se as dimensões de uma chácara retangular e a distância entre os moirões colocados em seu perímetro, sendo necessário determinar a quantidade total de moirões existentes. Os outros três problemas estão relacionados com o cálculo do volume de um paralelepípedo. A partir das medidas de comprimento, largura e altura (espessura ou profundidade) de objetos ou de outros elementos em situações contextualizadas, propõe-se o cálculo de volume e se explora a transformação de unidades de medida de comprimento. A importância do domínio do cálculo volumétrico era apontada por RAMBO (1994).
No Quadro 7, apresentam-se algumas relações entre as antigas medidas brasileiras e as medidas do sistema métrico, observadas nas edições da Terceira Aritmética:
Quadro 7. Relação entre as antigas medidas brasileiras e o sistema métrico.

Fonte.Série Concórdia, 1949, pp. 28-29.
Observam-se no Quadro 7, as antigas medidas brasileiras de comprimento, superfície e volume. As medidas de comprimento observadas são: a légua, a quadra, a braça, a vara, o palmo, a polegada, a jarda e o pé, e estão relacionadas com a principal unidade de medida de comprimento, o metro (m). As antigas medidas de superfície estão relacionadas como metro quadrado (m²), sendo elas: a braça quadrada (bra²), a quadra quadrada e a quarta de terra de milho. Estas unidades de medida de superfície eram usadas com frequência na representação de áreas de terras nas regiões coloniais. Aponta-se que o texto desta aritmética sobre as medidas de superfície é redundante ao considerar que as medidas de superfície são quadrados cujos lados têm igual comprimento seja qual for a medida linear. As antigas medidas de superfície apresentadas são: a braça cúbica, a vara cúbica e o pé cúbico, ambas estão relacionadas com o metro cúbico (m³), principal unidade de medida de volume. Com a gradativa adoção das medidas do sistema métrico, as antigas medidas brasileiras passaram a ser menos utilizadas, observando-se o seu uso em situações muito específicas, como por exemplo, aparelhos de televisão e monitores de computador costumam ser vendidos com medidas da diagonal em polegadas.
A última unidade de estudo das duas edições da Terceira Aritmética, denomina-se geometria prática, com ênfase nas medidas de superfície – explorando-se a superfície do quadrado, retângulo, trapézio, triângulo e círculo – e nas medidas dos corpos – explorando-se o volume do cubo, prisma etronco de cone. A Figura 3 ilustra a introdução ao estudo das medidas de superfície e o da superfície do quadrado com um exemplo e exercícios que sugerem a construção da figura para determinação da superfície de cada quadrado:
Figura 3 Medidas de superfície e o quadrado.
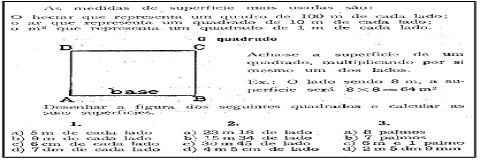
Fonte.Série Ordem e Progresso, [193-], p. 135.
A Figura 3 apresenta as medidas de superfície mais usadas: o hectare (ha), o are (ar) e o metro quadrado (m²) e sua relação com o metro quadrado, ou seja, 1 ha = 10000 m² e 1 ar = 100 m². Observa-se a representação geométrica de um quadrado, a descrição do procedimento para determinação da superfície de um quadrado e um exemplo. Em seguida, propõe-se desenhar quadrados com diferentes medidas do sistema métrico e com antigas medidas brasileiras e calcular suas superfícies. Embora não esteja escrito, o desenho dos quadrados pode ser apenas uma representação ou um desenho em escala, devido às dimensões indicadas. Esta proposta de estudo é semelhante, nas terceiras aritméticas, para as superfícies do retângulo, trapézio, retângulo e círculo, e para o estudo do volume de corpos: cubo, prisma e tronco de cone.
Na Figura 4 se apresenta uma proposta de estudo para a circunferência e o círculo:
Figura 4 A circunferência e o círculo.

Fonte.Série Ordem e Progresso, [193-], p. 138.
A Figura 4 ilustra a representação de uma circunferência e os seus elementos, diâmetro e raio, sem apresentar a relação entre ambos. Descreve como encontrar a circunferência de um círculo e traz um exemplo. Observa-se que o número 3,1416..., chamado de Pi, não é representado pela letra grega π e também não se faz referência à origem do mesmo no excerto. Apresenta-se a regra para determinação da área de um círculo e um exemplo. Neste exemplo, fica subentendido que a medida do diâmetro é o dobro da medida do raio, ou que a medida do raio é a metade da medida do diâmetro, pois é citado que o diâmetro sendo 80 cm, o raio será 40 cm.
O Quadro 8 apresenta o estudo do volume de um tronco de cone, observado nas duas edições da Terceira Aritmética:
Quadro 8. Volume de um tronco de cone.

Fonte.Série Ordem e Progresso, [193-], p. 140.
O exemplo, descrito no Quadro, 8 traz um procedimento de cálculo para o volume de um tronco de cone que resulta num valor aproximado do volume real do tronco com as dimensões citadas. Enquanto que o livro apresenta como resposta o valor aproximado de 1,539384 m³, o valor mais exato seria 1,549852 m³. Observa-se que a proposta do livro é determinar o volume do tronco de cone de uma forma mais prática, sem uso de relações algébricas, possibilitando que o aluno aplique este conhecimento em situações concretas na colônia, especialmente no cálculo de volume de madeira. De acordo com RAMBO (1994), o trabalho com madeira nas colônias só podia ser confiável com o domínio dos rudimentos do cálculo volumétrico nas suas mais diversas formas. Acrescenta-se que:
A cubagem da madeira é uma prática presente na vida das/os trabalhadoras/es rurais, consistindo no cálculo de quantos cúbicos tem numa árvore, num mato ou numa carga de caminhão. É utilizada para avaliar a quantia necessária de árvores que devem ser abatidas para serem transformadas em lenha, em tábuas para a construção de casas ou abrigos de animais, nos projetos de reflorestamento, na compra e venda de áreas arborizadas e nas negociações que a gente faz com os homens das serrarias. (KNIJNIK, 1996, pp. 52)
No Quadro 9 se apresentam problemas sobre geometria prática, encontrados nas duas edições da Terceira Aritmética:
Quadro 9.Problemas sobre geometria prática.

Fonte. Série Concórdia, 1949, pp. 142-143.
No Quadro 9 são apresentados problemas em diferentes contextos reais, envolvendo conhecimentos de geometria com ênfase no cálculo de área e de volume, além de envolver a transformação de unidades de medida e operações comerciais. Estes cinco problemas são parte da aplicação dos conteúdos de geometria prática desenvolvidos nas edições da Terceira Aritmética e mostram como os autores se preocupavam em propor atividades que contribuíssem para apropriação dos conhecimentos matemáticos pelos alunos (CHARTIER, 1990). O Quadro 10 relaciona a determinação da raiz quadrada com a geometria:
Quadro 10.Problemas sobre geometria prática.

Fonte. Série Ordem e Progresso, [193-], p. 140.
No Quadro 10, apresenta-se uma relação entre número quadrado e raiz quadrada, associando-se esta ideia com a representação geométrica de um quadrado. O estudo é ilustrado com um exemplo para determinação da raiz quadrada de 169. A proposta é representar geometricamente o quadrado do número 13, fazendo a sua decomposição em dezena e unidades (a = 10 e b = 3) e sua representação com um quadrado maior (a²), dois retângulos (2ab) e um quadrado menor (b²). Observa-se o quadrado da dezena (a² = 10² = 10 x 10 = 100), o dobro da dezena pelas unidades (2ab = 2 x 10 x 3 = 60) e o quadrado das unidades (b² = 3² = 3 x 3 = 9). Logo, 13 é a raiz quadrada do número quadrado 169. De acordo com o excerto, essas relações são válidas para o quadrado de números compostos de dezenas e unidades. Tomando-se como exemplo o quadrado de 28, tem-se:
28 = 20 + 8, ou seja, a = 20 e b = 8.
- o quadrado das dezenas: a² = 20² = 20 x 20 = 400;
- o dobro das dezenas pelas unidades: 2ab = 2 x 20 x 8 = 320;
- o quadrado das unidades: b² = 8² = 8 x 8 = 64. Portanto, 28² = (20 + 8)² = 20² + 2 x 20 x 8 + 8² = 400 + 320 + 64 = 784, ou seja, 28 é a raiz quadrada do número quadrado 784.
A representação geométrica de um número quadrado traz implicitamente a ideia de um produto notável, (a + b)² = a² + 2ab + b², relacionando conhecimentos de aritmética, geometria e álgebra.
A representação geométrica de um número quadrado traz implicitamente a ideia de um produto notável, (a + b)² = a² + 2ab + b², relacionando conhecimentos de aritmética, geometria e álgebra.
Considerações finais
Partindo do referencial teórico-metodológico da história cultural se investigou a geometria nas aritméticas da série Ordem e Progresso e da série Concórdia, editadas pela IELB, através da Casa Publicadora Concórdia, na primeira metade do século XX, para suas escolas paroquiais no RS. Neste contexto missionário e de formação geral, a Igreja Luterana editou livros didáticos de acordo com seus princípios morais e educacionais, adaptando-se ao processo de nacionalização do ensino.
Na investigação realizada se constatou que as edições da Primeira Aritmética da série Ordem e Progresso e da série Concórdia não fazem referência ao estudo da geometria, pois as propostas de ensino dos autores estavam voltadas para as quatro operações elementares com os números naturais até 100. Nas edições da Segunda Aritmética se verificou que os conhecimentos geométricos foram desenvolvidos de forma prática e contextualizada e estavam relacionados com medidas de comprimento, desenhos em escala, medidas de superfície e formas geométricas planas.
Nas edições da Terceira Aritmética se observou que os conhecimentos geométricos estavam relacionados com medidas de comprimento, medidas de superfície, medidas de volume e com as antigas medidas brasileiras. Estes conhecimentos também foram desenvolvidos de forma prática e contextualizados com a realidade dos alunos, além de se observarem relações com outros conhecimentos matemáticos, como a determinação da raiz quadrada.
Considerando-se o referencial da história cultural, destaca-se que os autores das aritméticas da série Ordem e Progresso e da série Concórdia se valeram da estratégia de apresentar propostas de ensino da geometria de forma prática e associada com situações reais para que os alunos das escolas paroquiais luteranas gaúchas se apropriassem desses conhecimentos matemáticos, e no futuro, realizassem a administração correta do seu orçamento familiar e o gerenciamento da sua propriedade rural. Este estudo histórico sobre a geometria nas aritméticas editadas para as escolas paroquiais luteranas gaúchas, do século XX, possibilitou um adentramento na cultura escolar, num lugar e num tempo determinados, contribuindo para a História da Educação Matemática.
Referências
ARENDT, I. C. Educação, religião e identidade étnica: o Allgemeine Lehrerzeitung e a escola evangélica alemã no Rio Grande do Sul. São Leopoldo: Brasil, 2008
ARENDT, I. C. Representações de Germanidade, Escola e Professor no Allgemeine Lehrerzeitung für Rio Grande do Sul [Jornal Geral para o Professor no Rio Grande do Sul]. 292 pp. Tese de Doutorado em História, Universidade do Vale do Rio dos Sinos, São Leopoldo: Brasil, 2005
CHARTIER, R. A História Cultural: entre práticas e representações. Lisboa: Portugal, 1990.
CHERVEL, A. História das disciplinas escolares – reflexões sobre um campo de pesquisa. Teoria & Educação, Porto Alegre, n. 2, p. 177-229, 1990.
GOERL, O. A. Série Concórdia: Primeira Aritmética. Porto Alegre: Brasil, [194-a].
GOERL, O. A. Série Concórdia: Segunda Aritmética. Porto Alegre: Brasil, [194-b].
JULIA, D. A cultura escolar como objeto histórico. Revista Brasileira de História da Educação, Campinas, n. 1, p. 9-43, jan./jun. 2001.
KNIJNIK, G. Exclusão e resistência: educação matemática e legitimidade cultural. Porto Alegre: Brasil, 1996.
KREUTZ, L. Livros escolares e imprensa educacional periódica dos imigrantes alemães no Rio Grande do Sul, Brasil 1870-1939. Revista Educação em Questão, Natal, v. 31, n. 17, p. 24-52, jan./ abr. 2008.
KREUTZ, L. Material didático e currículo na escola teuto-brasileira. São Leopoldo: Brasil, 1994
KREUTZ, L. O professor paroquial: magistério e imigração alemã. Porto Alegre: Brasil, 1991.
KREUTZ, L.; ARENDT, I. C. (Org.). Livros escolares das escolas de imigração alemã no Brasil (18321940). Acervo documental e de pesquisa. São Leopoldo: Brasil, 2007. 3 CD-ROM.
KUHN, M. C.O ensino da Matemática nas escolas evangélicas luteranas do Rio Grande do Sul durante a primeira metade do século XX. 466 pp. Tese de Doutorado em Ensino de Ciências e Matemática – Universidade Luterana do Brasil, Canoas, 2015.
LEMKE, M. D. Os princípios da educação cristã luterana e a gestão de escolas confessionárias no contexto das ideias pedagógicas no sul do Brasil (1824 – 1997). Canoas: Brasil, 2001.
MAURO, S. Uma história da matemática escolar desenvolvida por comunidades de origem alemã no Rio Grande do Sul no final do século XIX e início do século XX. 257 pp. Tese de Doutorado em Educação Matemática – Universidade Estadual Paulista, Rio Claro, 2005.
PROST, A. Doze lições sobre a História. Belo Horizonte, Autêntica, 2008.
RAMBO, A. B. A escola comunitária teuto-brasileira católica. São Leopoldo: Brasil, 1994.
RAMBO, A. B.A escola comunitária teuto-brasileira católica: a associação de professores e a escola normal. São Leopoldo: Brasil, 1996.
ROCHE, J. A Colonização Alemã e o Rio Grande do Sul. Porto Alegre: Brasil, 1969. v. 1 e v. 2.
SÉRIE Concórdia: Segunda Aritmética. Porto Alegre: Brasil, 1948.
SÉRIE Concórdia: Terceira Aritmética. Porto Alegre: Brasil, 1949.
SÉRIE Ordem e Progresso: Terceira Arithmetica. Porto Alegre: Brasil, [193-].
STRELOW, F. Série Ordem e Progresso: Primeira Aritmética. Porto Alegre: Brasil, [193-].
UNSERE SCHULE. Porto Alegre: Brasil, 1933-1935.
VALENTE, W. R. História da Educação Matemática: interrogações metodológicas. REVEMAT – Revista Eletrônica de Educação Matemática, UFSC, v. 2.2, p. 28-49, 2007.
VALENTE, W. R.; PINHEIRO, N. V. L. Chega de decorar a tabuada! – As cartas de Parker e a árvore do cálculo na ruptura de uma tradição. Educação Matemática em Revista - RS, Canoas, v. 1, n. 16, p. 22-37, 2015.
WANDERER, F. Escola e Matemática Escolar: mecanismos de regulação sobre sujeitos escolares de uma localidade rural de colonização alemã no Rio Grande do Sul. 228 pp. Tese de Doutorado em Educação – Universidade do Vale do Rio dos Sinos, São Leopoldo, 2007.
WARTH, C. H. Crônicas da Igreja: Fatos Históricos da Igreja Evangélica Luterana do Brasil (1900 a 1974). Porto Alegre: Brasil, 1979.
WEIDUSCHADT, P. A revista “O Pequeno Luterano” e a formação educativa religiosa luterana no contexto pomerano em Pelotas – RS (19311966). 273 pp. Tese de Doutorado em Educação – Universidade do Vale do Rio dos Sinos, São Leopoldo, 2012.
WEIDUSCHADT, P.O Sínodo de Missouri e a educação pomerana em Pelotas e São Lourenço do Sul nas primeiras décadas do século XX: identidade e cultura escolar. 255 pp. Dissertação de Mestrado em Educação – Universidade Federal de Pelotas, Pelotas, 2007.
Licencia
Góndola, Ens Aprend Cienc. es una publicación de acceso abierto, sin cargos económicos para autores ni lectores. La publicación, consulta o descarga de los contenidos de la revista no genera costo alguno para los autores ni los lectores, toda vez que la Universidad Distrital Francisco José de Caldas asume los gastos relacionados con edición, gestión y publicación. Los pares evaluadores no reciben retribución económica alguna por su valiosa contribución. Se entiende el trabajo de todos los actores mencionados anteriormente como un aporte al fortalecimiento y crecimiento de la comunidad investigadora en el campo de la Enseñanza de las Ciencias.
A partir del 01 de diciembre de 2018 los contenidos de la revista se publican bajo los términos de la Licencia Creative Commons Atribución–No comercial–Compartir igual 4.0 Internacional (CC-BY-NC-SA 4.0), bajo la cual otros podrán distribuir, remezclar, retocar, y crear a partir de la obra de modo no comercial, siempre y cuando den crédito y licencien sus nuevas creaciones bajo las mismas condiciones.
Los titulares de los derechos de autor son los autores y la revista Góndola, Ens Aprend Cienc. Los titulares conservan todos los derechos sin restricciones, respetando los términos de la licencia en cuanto a la consulta, descarga y distribución del material.
Cuando la obra o alguno de sus elementos se halle en el dominio público según la ley vigente aplicable, esta situación no quedará afectada por la licencia.
Asimismo, incentivamos a los autores a depositar sus contribuciones en otros repositorios institucionales y temáticos, con la certeza de que la cultura y el conocimiento es un bien de todos y para todos.




















