DOI:
https://doi.org/10.14483/23464712.12500Publicado:
2018-05-03O ensino dos números racionais por meio de atividades de pesquisa e investigação: buscando desenvolver o pensar
Teaching of Rational Numbers Through Inquiry and Research Activities: Looking for Thinking Development
La enseñanza de los números racionales por medio de actividades de indagación e investigación: buscando desarrollar el pensamiento
Palabras clave:
Rational numbers, teaching, research, investigation. (en).Palabras clave:
Números racionales, enseñanza, indagación, investigación. (es).Palabras clave:
Números racionais, ensino, pesquisa, investigação. (pt).Referencias
Alarcão, I. Professores reflexivos em uma escola reflexiva. Cortez, São Paulo, Brasil. 2011.
Brasil. Parâmetros Curriculares da Matemática: Matemática. MEC, Brasília, Brasil. 1998.
Brasil. Lei de Diretrizes e Bases da educação Nacional. LDB 9394/96. Disponível em: http://www.planalto.gov.br/ccivil_03/Leis/L9394.htm. Acesso em: 02 set. 2015.
Borba, M. C.; Silva, R.S. R.; Gadanidis, G. Fases das tecnologias digitais em Educação Matemática. Autêntica, Belo Horizonte, Brasil. 2015.
Costa, M. V. (org). A escola tem futuro? DP&A, Rio de Janeiro, Brasil. 2003.
D'Ambrósio. U. Educação Matemática: da Teoria à prática. 19 ed. Papirus, Campinas, SP, Brasil. 2010.
Demo, P. Metodologia da Investigação em Educação. Ibpex, Curitiba, Brasil. 2005.
Demo, P. Educar pela pesquisa. Editora Autores Associados, Campinas, Brasil. 2015.
Felcher, C. D. O; Pinto, A. C.; Ferreira, A. L. A. O uso do Facebook como Ambiente Virtual de Aprendizagem para o ensino dos números racionais. Revista Paranaense de Educação Matemática, v. 6, n. 10, pp. 246-271. 2017.
Gil, A. C. Métodos e Técnicas de Pesquisa Social. 6 ed. Atlas, São Paulo, Brasil. 2012.
Gonzáles, J, Arrieche, M. Significados Institucionales y Personales de lãs Fracciones em Educación Básica. In: Acta Latino Americana de Matemática Educativa. v. 18. México. 2005.
Gomes, M. L. M. História do ensino da Matemática: uma introdução. CEAD-UFMG, Belo Horizonte, Brasil. 2012.
Haydt, R. C. C. Avaliação do processo ensino-aprendizagem. Ática, São Paulo, Brasil. 1998.
Irwin, C. K. Using Everyday Knowledge of Decimals to Enhance Understanding. Journal for Research in Mathematics Education. Auckland, v. 32, n. 4, pp. 399-420. 2001.
Lopes, A. J. O que os Nossos Alunos Podem Estar Deixando de Aprender sobre Frações, quando Tentamos Ensinar Frações. Revista Bolema, Rio Claro, SP, n. 31, pp. 1-22. 2008.
Maranhão, M. C; Igliori, S. B. C. Registros de representação e números racionais. In: MACHADO, S. D. A. Aprendizagem em matemática - registros de representação semiótica. Papirus, São Paulo, Brasil. 2003, pp. 57-70.
Meneguetti, R. C. G; Nunes, A. C. A. Aplicação de uma proposta pedagógica no ensino dos números racionais. Educação Matemática em Revista, n. 20-21, pp. 77- 86, 2006.
Primo, A. Interação mediada por computador. Sulina, Porto Alegre, Brasil. 2011.
Ponte, J. P.; Brocardo, J.; Oliveira, H. Investigações Matemáticas na Sala de Aula. 3 ed. Autêntica, Belo Horizonte, Brasil. 2013.
Rickes, J., Silveira, D. Material concreto manuseável: um motivador para o ensino de frações. In.: FONSECA, M.S. et al. (org). Matemáticas: educação e pesquisa. Ed. Da Universidade Federal de Pelotas, Pelotas, Brasil. 2014. pp. 106-123.
Selbach, S. Matemática e didática. Vozes, Petrópolis, Brasil. 2010.
TRIPP, D. Pesquisa-ação: uma introdução metodológica. Revista Educação e Pesquisa, São Paulo, v. 31, n. 3, pp. 443-466, set./dez. 2005. Disponível em: <http://www.scielo.br/pdf/ep/v31n3/a09v31n3.pdf. Acesso em: 01/12/2014.
Thiollent, M. A metodologia da pesquisa-ação. Cortez, São Paulo, Brasil. 2011.
Toledo, M.; Toledo, M. Teoria e prática de Matemática: como dois e dois. FTD, São Paulo, Brasil. 2009.
Vygotsky, L. A formação social da mente: o desenvolvimento dos processos psicológicos superiores. Martins Fontes, São Paulo, Brasil. 1998.
Cómo citar
APA
ACM
ACS
ABNT
Chicago
Harvard
IEEE
MLA
Turabian
Vancouver
Descargar cita
DOI: http://doi.org/10.14483/23464712.12500
O ENSINO DOS NÚMEROS RACIONAIS POR MEIO DE ATIVIDADES DE PESQUISA E INVESTIGAÇÃO: BUSCANDO DESENVOLVER O PENSAR
TEACHING OF RATIONAL NUMBERS THROUGH INQUIRY AND RESEARCH ACTIVITIES: LOOKING FOR THINKING DEVELOPMENT
LA ENSEÑANZA DE LOS NÚMEROS RACIONALES POR MEDIO DE ACTIVIDADES DE INDAGACIÓN E INVESTIGACIÓN: BUSCANDO DESARROLLAR EL PENSAMIENTO
Carla Denize Ott Felcher*, André Luis Andrejew Ferreira**
Cómo citar este artículo: Ott Felcher, C. D. y Andrejew Ferreira, A. L. (2018). O ensino dos números racionais por meio de atividades de pesquisa e investigação: buscando desenvolver o pensar. Góndola, Enseñanza y Aprendizaje de las Ciencias, 13(2), 236-250. DOI: http://doi.org/10.14483/23464712.12500
Recibido: 12 de septiembre de 2017 / Aprobado: 23 de enero de 2018
* Licenciada em Matemática – UCPel. Mestra em Ensino de Ciências e Matemática - UFPel. Doutoranda em Educação em Ciências – UFRGS. Professora de Matemática da Rede Pública Municipal e também em cursos de Pós-Graduação Especialização na área da Educação. Correio eletrônico: carlafelcher@gmail.com
** Graduado em Matemática Aplicada e Computacional – UFRGS. Mestre em Ciência da Computação – UFRGS. Doutor em Informática na Educação - UFRGS. Professor do Programa de Pós-Graduação em Ensino de Ciências e Matemática (Mestrado Profissional) da Faculdade de Educação/UFPel. Correio eletrônico: andrejew.ferreira@gmail.com
Resumo
Este artigo apresenta os resultados de uma pesquisa de mestrado que estudou o ensino dos números racionais na perspectiva de desenvolvimento do pensar, considerando o conteúdo como componente curricular necessário. Para tal, desenvolveu-se uma pesquisa-ação, em uma escola pública do município de Canguçu, onde foi criado um grupo fechado na rede social Facebook, denominado F@ceMAT, servindo como um Ambiente Virtual de Aprendizagem. Nesse grupo foram postadas imagens, textos, vídeos, jogos didáticos, objetos de aprendizagem, pesquisas, desafios e principalmente situações problema. Por meio dessas, priorizou-se a pesquisa e a investigação, levando o aluno a ler, interpretar, elaborar, calcular, reformular, proporcionando a interação entre os sujeitos de pesquisa e, assim desenvolver o pensar. Percebeu-se a dificuldade dos alunos na compreensão e resolução do proposto, mas também o envolvimento, a participação de cada um e, a importância da interação entre os pares, aluno e aluno, aluno e professor, de modo que aos poucos os alunos foram esclarecendo as dúvidas e conseguindo desenvolve-las. Concluiu-se que as atividades de pesquisa e investigação foram favoráveis ao ensino e aprendizagem dos números racionais, contribuindo para a mudança do paradigma tradicional de ensino ainda tão limitado a resolver listas de exercícios.
Palavras chaves: números racionais, ensino, pesquisa, investigação.
Abstract
This paper presents results of a master research that investigated the rational numbers teaching in the perspective of thinking development, it was considering the content as a necessary curricular component. For this, an action research was developed, in a public school of the Canguçu city. A closed group was created on the social network Facebook, named F@ ceMAT. It was a virtual environment of learning. In this group we posted, images, texts, videos, didactic games, learning objects, research results, challenges and mainly situations problems. Through these diversified activities, it was looked for to prioritize the investigation and research process, stimulate the student to read, to interpret, to elaborate, to calculate, to reformulate, providing interaction between the researcher and students. Thus, looking for thinking development. It was perceived student’s difficulties in understanding and resolve the problems proposed, but also the involvement, the participation of each one and, the importance of interaction between the peers, pupil and pupil, pupil and teacher so that gradually the pupils were clarifying doubts and achieving develop them. We concluded that inquiry and research activities were good to teaching and learning rational numbers, contributing to changing traditional teaching paradigm, which still so limited to solving exercise lists.
Keywords: rational numbers, teaching, research, investigation.
Resumen
Este artículo presenta resultados de una investigación de maestría que estudió la enseñanza de los números racionales en la perspectiva de desarrollo del pensamiento, considerando el contenido como componente curricular necesario. Para ello, desarrollamos una investigación- acción en una escuela pública del municipio de Canguçu, para lo cual creamos un grupo cerrado en la red social Facebook, denominado F@ceMAT, lo que nos permitió crear un ambiente virtual de aprendizaje. En este grupo dispusimos imágenes, textos, videos, juegos didácticos, objeto de aprendizaje, investigaciones, desafíos y principalmente situaciones problema. Por medio de ello, priorizamos la búsqueda y la indagación llevando al estudiante a leer, interpretar, elaborar, calcular y reformular, lo que propició la interacción entre los sujetos de investigación para desarrollar su pensamiento. Percibimos la dificultad de los alumnos en la comprensión y solución de los ejercicios propuestos, así como su compromiso y el reconocimiento de la importancia de la interacción entre pares, alumno/alumno, docente/alumno, de tal forma que los estudiantes pudieron aclarar dudas y desarrollar ideas. Concluimos que las actividades de búsqueda e indagación contribuyeron a la enseñanza y el aprendizaje de los números racionales, posibilitando el cambio de paradigma tradicional de enseñanza, el cual aún se limita a resolver listas de ejercicios.
Palabras clave: números racionales, enseñanza, indagación, investigación.
Introdução
As discussões a respeito do currículo escolar são pertinentes e necessárias e, quando o alvo é a disciplina de Matemática, no sentido restrito de grade curricular, as discussões são ainda mais intensas assinalando os conteúdos como engessados, o que para alguns professores não permite um trabalho diferenciado, cabendo a esses vencê- los, apenas. Sendo assim, Moreira, em entrevista a COSTA (2003), diz que embora haja um currículo e, conforme a Lei de Diretrizes e Bases Educação Nacional (LDBEN) 9394/96, com uma base nacional comum, “escolhas não são totalmente determinadas previamente, algum grau de liberdade se tem” (COSTA, 2003 p. 56).
Registra-se que atualmente não há uma Base Nacional Comum consolidada e em prática, sendo assim, os Parâmetros Curriculares Nacionais (BRASIL, 1998) servem como diretrizes curriculares e trazem a Matemática organizada em quatro blocos, os quais se constituem de Números e operações, Espaço e forma, Grandezas e Medidas, e Tratamento da Informação.
Moreira em entrevista a COSTA (2003) ressalta que o professor tem certo grau de liberdade para desenvolver o seu trabalho, assim pode priorizar determinados conceitos em detrimento de outros, caso essa organização seja justificável. Para D’AMBRÓSIO (2010), o professor precisa elaborar uma justificativa para cada um dos tópicos do programa e esta não pode se resumir ao argumento de que servirá de requisito para o próximo conteúdo a ser estudado.
A respeito dos conteúdos curriculares, SELBACH (2010) argumenta que não é possível conceber o pensamento retrógrado de que há um currículo a ser cumprido e, se o aluno não o aprende, a culpa é sua. Os conteúdos são o meio por onde os alunos aprendem e manifestam as diferentes inteligências. Sendo assim: “Uma escola ou um professor sem conteúdo é escola sem propósito e objetivo, é professor sem missão, aula sem foco. “Conteúdo” não é coisa que se acumula, mas ferramenta com a qual se aprende a aprender e, por saber a aprender, conseguir transformar” (SELBACH, 2010 p. 49-50).
Avaliando a importância dos conteúdos curriculares, SELBACH (2010) ressalta que é preciso definir de qual matemática se está falando, identificando aquela que vai ser útil ao aluno em diferentes níveis da educação, já que a matemática como área do conhecimento, possui indiscutível valor formativo, sem falar que é uma ferramenta essencial em qualquer profissão.
A partir dessas considerações sobre conteúdos curriculares e do entendimento de que números racionais são de relevância na formação do educando, embora haja aqueles que saem dos bancos escolares sem o devido entendimento do conceito, o presente artigo tem por objetivo investigar o ensino dos números racionais numa perspectiva que considera este conteúdo curricular como aporte para desenvolver o pensar.
1. Os números racionais como conteúdo curricular
Cabe questionar, nesse contexto, qual espaço dentro dessa grade curricular que os números racionais na forma fracionária ocupam. Os números racionais são importantes para a formação acadêmica do aluno? Eles sempre foram ensinados? Como é a relação dos alunos com esse conteúdo matemático?
Para abordar os questionamentos acima, apresenta- se uma retrospectiva histórica dos números racionais, GOMES (2012), baseada em livros didáticos analisados por ela mesma, traz que muitas alterações aconteceram em relação à abordagem dos números, em especial, dos números racionais. Assim, segundo a mesma autora, primeiramente a conceituação de número coloca ênfase no aspecto do número racional como expressão da medição de uma grandeza. Essa expressão é um número inteiro ou fracionário chamado de número comensurável.
Em um segundo momento, os livros destacam com menor ênfase o número como resultado da medição de uma grandeza. Dessa maneira, a ligação entre a noção de fração e a medição de comprimentos torna-se mais fraca. A denominação números comensuráveis não é mais empregada, e, sim, fração, sendo que, para “a fração é, sobretudo, uma ou mais das partes iguais em que se divide a unidade, unidade esta que não é mais sempre representada por um segmento de reta” (GOMES, 2012 p. 48).
No terceiro momento, não se encontra mais nos livros a noção de grandeza. Logo, “O número (natural) é apresentado como uma propriedade comum a dois conjuntos entre os quais se pode estabelecer uma correspondência biunívoca” (GOMES, 2012 p. 12). A ideia da fração como uma ou mais partes iguais em que se divide a unidade perde espaço em favor da fração na forma a/b, considerando a e b um par ordenado de inteiros com b diferente de zero.
Desse modo, a evidência está para uma abordagem formal, completamente diferente daquela realizada no primeiro momento, adota-se um enfoque formal: “ou o racional é apresentado como o número definido pela classe de equivalência de uma fração, ou é definido como qualquer número que possa ser colocado na forma p/q, sendo p e q inteiros quaisquer e q não nulo” (GOMES, 2012 p. 47).
A definição acima parece reduzir os números racionais em algo simples, porém a realidade demonstra que o trabalho com esse conjunto numérico envolve diversas dificuldades no que tange à aprendizagem do aluno, principalmente no entendimento do que são os números racionais, assim, é possível encontrar alunos que no Ensino Médio e até no Superior surpreendem-se ao saber que a fração um meio e o número decimal cinco décimos são localizados exatamente no mesmo ponto da reta numérica. Portanto, os dois números racionais embora representados de forma diferente tem o mesmo valor.
Reforçando e complementando, os PCNs (1998) relatam que embora números racionais sejam conteúdo do Ensino Fundamental, o que se observa é que essa dificuldade persiste até mesmo no Ensino Superior, em que os alunos chegam sem entender o significado desses conceitos e com dificuldades nos cálculos, principalmente em relação à representação decimal. Assim, torna-se evidente que essas dificuldades podem acarretar prejuízos à progressão nos estudos, justificando questionar o porquê de tamanha dificuldade no ensino desse conteúdo curricular.
Buscando compreender a justificativa para a dificuldade de compreensão do que são os números racionais, HILTON (apud LOPES, 2008), relata uma conferência proferida por esse, em 1980 nos Estados Unidos, é bastante enfático ao dizer que as frações deveriam ser ensinadas como parte do currículo elementar e, não somente em momentos estanques, configurando capítulo de livro ou um tema o currículo elementar da Matemática. Assim, o exposto por HILTON (apud LOPES, 2008) afirma que nunca deveríamos ter ensinado as frações da forma como foram e, ainda, são ensinadas, referindo-se aqui ao que os livros didáticos trazem como aplicações das frações enganosas. Um exemplo apresentado pode ser observado a seguir - “João comeu 3/17 avos de um bolo, seu irmão comeu 5/9 do que restou... Quanto sobrou para sua irmã?” (p. 23).
Em relação às dificuldades que envolvem a aprendizagem dos racionais, percebe-se que no Ensino Fundamental, mais especificamente nos anos iniciais, quando começam os números racionais, há uma ruptura com os números naturais. De acordo com os PCN (BRASIL, 1998), o aluno que raciocina sobre os números racionais como se fossem naturais enfrenta vários obstáculos, a começar pela representação que pode ser feita por infinitas escritas fracionárias; a comparação entre racionais não é mais tão clara e simples quanto nos naturais; o “tamanho” da escrita numérica também começa a deixar dúvidas, sem falar que as operações apresentam outras regras, e antecessor e sucessor (número que vem antes e o que vem depois) praticamente não se fala mais.
Para LOPES (2008), além do estatuto epistemológico das frações, a própria representação também é um obstáculo, afinal, associar dois números inteiros separados com um traço não é tão trivial assim. Então, quando associados dois inteiros e entre eles um traço, os números deixam de ser inteiros? Este deve ser um frequente questionamento dos alunos. Gonzáles e Arrieche citam um trabalho que investigou a introdução do conceito de frações na escola:
[...] um trabalho de investigação sobre a introdução da noção de frações a partir de problemas de divisão para crianças de primeira e segunda série do ensino primário, também inclina-se a determinação de obstáculos. Entre suas conclusões expõe que uma das limitações identificadas é a prematura inclusão do nível simbólico nestas primeiras séries da educação. (GONZÁLES, ARRIECHE, 2005 p. 359)
Já os PCNs (BRASIL (1998)) enfatizam a necessidade de iniciar o trabalho com frações entre o 4º e o 7º ano, de modo que os alunos percebam que os números naturais são insuficientes para a resolução de certas situações. Esse documento sugere que essa percepção aconteça a partir de situações-problemas apresentadas pelo professor, em que os números naturais sejam incapazes de exprimir o resultado. Assim, os alunos são apresentados aos números na forma racional.
O que se percebe é que, no contexto da vida diária, a utilização de frações está mais relacionada à vida adulta, resumindo-se em grande medida às frações do tipo um meio, um terço, um quarto. No entanto, na escola empregam-se frações bem distintas destas, como por exemplo, 15/19. Curiosamente, um estudo realizado por IRWIN (2001) traz como resultado que crianças com menos idade trabalharam mais facilmente com os decimais, em relação às crianças mais velhas, que já tinham estudado os decimais como conteúdo da escola.
Entre os principais resultados destas entrevistas foi que as crianças de 8 anos indicaram um conhecimento amplo do uso diário dos decimais: falaram sobre vê-los em estatísticas dos esportes, sobre gráficos hospitalares, nas lojas, cheques nos bancos (incluindo conversão de moeda), em calculadoras, em livros, como uma posição em uma corrida (1.4 km), e em um frasco de 1,5 litros de bebida. Entretanto crianças com 10 anos ou mais velhas, que tinham tido contato com decimais na Escola, tinham uma visão bem mais limitada dos contextos diários para os decimais apresentando exemplos com dinheiro e do contexto Escolar. Estas crianças mais velhas poderiam escrever e ler um número que incluísse uma fração decimal desde que a tivessem visto na Escola. (IRWIN, 2001 p. 3)
O estudo de Irwin é claro no que se refere à participação da escola na aprendizagem dos números racionais. Para o autor, as crianças que não haviam aprendido o conteúdo na escola, fizeram diversas associações entre os decimais e situações da vida cotidiana.
Talvez aqui seja possível identificar um elemento facilitador para a aprendizagem, que seriam as situações cotidianas, assim como, usar tais situações para relacionar com as frações explicando que são formas de representações diferentes para uma mesma quantia, levando em consideração que para), “um aluno pode saber, por exemplo, que deve dividir 1 por 4 para obter a representação decimal do racional ¼, mas pode ser que não reconheça 0,25 como outro representante do mesmo número racional” (MARANHÃO, IGLORI, 2003 p. 60).
O que se percebe nesse caso é a não construção ou a construção equivocada do conceito de fração, talvez resultado de práticas calcadas em regras, ou ainda, conforme o que já foi exposto em relação à introdução precoce do conceito sem que o aluno tenha maturidade para compreendê-lo. A construção correta do conceito de fração mostra-se de extrema relevância, pois, conforme aponta os PCNs (1998), embora no cotidiano o uso de frações seja menos frequente, o conceito é utilizado em outros conteúdos, tais como: proporções, equações, sistemas, entre outros. Ainda, quando nos deparamos com uma dízima periódica, a representação na forma fracionária favorece um resultado mais preciso.
Além disso, LOPES (2008) acrescenta que o ensino de frações em apenas algumas séries específicas do fundamental, como acontece é um erro, pois desconsidera que o desenvolvimento da pessoa se estende dos 7 a 8 anos até os 14 e 15 anos. Assim, a sugestão do autor é que, na forma de um espiral, os currículos deveriam contemplar experiências com frações ao longo dos níveis fundamental e médio (Educação Básica).
2. Sobre o ensino dos números racionais
Visando a construção do conceito de número racional é importante que a criança possa manipular diferentes objetos, rompendo com a prática de colorir figuras, tão em voga ainda hoje. Desse modo, o aluno poderá realizar práticas tais como:
Repartir quantidades (discretas ou contínuas) em porções iguais, buscando seus próprios caminhos; Verificar se as porções obtidas são realmente iguais, por meio de comparação das quantidades, no caso de grandezas de natureza discreta, ou superposição das partes, no caso de grandezas de natureza continua; Conferir se a partição está completa, recompondo a coleção ou figura inicial. (TOLEDO, TOLEDO, 2009 p. 164)
A respeito da manipulação do material concreto, “a partir de nossa intervenção, percebemos que os conteúdos trabalhados com materiais de fácil manipulação ou visualização foram mais bem compreendidos pelos alunos do que os demais” (MENEGHETTI, NUNES, 2006 p. 83).
Ainda sobre como ensinar frações, LOPES (2008) propõe um conjunto de atividades cujo objetivo, entre outros, é o desenvolvimento do sentido numérico em grau crescente de complexidade, a ser explorado em todo o ensino fundamental, entre eles destacam-se apresentar aos alunos situações que possibilitem a problematização e exploração da noção de metade em contextos de comparação; explorar a metade da metade e, a metade da metade da metade; investigar o sentido das palavras que tenham a ideia de parte e explorar atividades de resolução de problemas focados na visualização.
A partir da leitura de LOPES (2008) percebe- -se a relevância de utilizar atividades de pesquisa e investigação para ensinar números racionais. E, neste sentido, os autores Demo e Ponte, Brocardo e Oliveira são fundamentais. Demo com a importância de uma prática pedagógica apoiada na pesquisa e, os demais, enfatizando as investigações em sala de aula.
Segundo DEMO (2015), a base da educação escolar deve ser a pesquisa e não a aula. Pesquisa que não pode ser confundida com práticas pontuais, tarefas com data marcada, costumeiramente em datas comemorativas. Nesse sentido, o autor alerta para a necessidade em distinguir pesquisa como atitude cotidiana e como resultado específico, pois, segundo ele:
Como atitude cotidiana, está na vida e constitui forma de passar por ela criticamente, tanto no sentido de cultivar a consciência crítica, quanto no de saber intervir na realidade de modo alternativo com base questionadora. [...] Como resultado específico, significa um produto concreto e localizado, como a feitura de um projeto pedagógico, ou de material didático próprio, ou de um texto com marcas científicas. (DEMO, 2015 p.15)
Assim, a pesquisa como atitude cotidiana é fundamental em todos os momentos da prática educativa, desmitificando a ideia de algo especial, realizado por pesquisadores em seus espaços reservados e, considerar que professor e aluno podem e devem desenvolver pesquisa.
Já, investigação “é procurar conhecer o que não se sabe”. (PONTE, BROCARDO, OLIVEIRA, 2013 p. 13). Inclusive, de acordo com os autores, trabalhar com investigação não significa necessariamente lidar com problemas muito difíceis, basta formularmos questões do nosso interesse e que não temos resposta e, responde-las de modo fundamentado e rigoroso.
Em se tratando de pesquisa e investigação, o PCN de Matemática, de 5ª a 8ª série, faz menção à importância destas para a aprendizagem matemática, relacionando-as com a Resolução de Problemas. Assim, entre os objetivos indicados para o ensino e aprendizagem dessa área do conhecimento, encontra- se a capacidade de investigação e resolução de problemas (BRASIL, 1998).
Nesta discussão, empregar-se-á os termos pesquisa e investigação, por entender que estas estão relacionadas, complementando-se e, assim em acordo “fala-se em investigação a propósito de atividades que envolvem uma procura de informação, por exemplo, fazer uma investigação ou pesquisa na Internet” (PONTE, BROCARDO, OLIVEIRA, 2013 p. 13).
Nesse contexto que privilegia pesquisa e investigação, a interação é de grande relevância. Segundo PRIMO (2011) interação é o envolvimento de duas ou mais pessoas, bem como a interação sujeito e objeto. Segundo PRIMO (2011), as interações podem ser reativas ou mútuas, sendo que a reativa é um tipo limitado de interação ou fechada, enquanto a mútua é criativa, aberta, de verdadeira troca. As primeiras acontecem pelo estímulo resposta e a segunda se dá através da negociação.
3. A organização do trabalho com números racionais
a. Metodologia e método
A metodologia empregada nessa investigação foi qualitativa através de pesquisa-ação, sendo o professor também o pesquisador, ou seja, ambos os papéis foram desenvolvidos por um único profissional. A pesquisa-ação, segundo DEMO (2005), é um tipo de pesquisa social que vem crescendo consideravelmente em educação, sendo que há envolvimento do pesquisador e pesquisado. Nesse contexto, professor e aluno, ambos buscam solução para os seus problemas.
A pesquisa-ação segundo GIL (2012) é uma proposta alternativa de pesquisa que busca obter resultados socialmente relevantes, no sentido de realmente contribuir com a realidade, transformando-a. Nesse método o pesquisador tem esta possibilidade, o que torna esse tipo de investigação tão interessante e merecedora de estudos e práticas. E, “é uma forma de investigação-ação que utiliza técnicas de pesquisa consagradas para informar à ação que se decide tomar para melhorar a prática” (TRIPP, 2005 p. 443).
Assim, a pesquisa-ação proporciona conhecer a realidade e também fazer intervenções através de ações mais significativas. Para THIOLLENT (2011), a pesquisa-ação permite que pesquisador e os participantes representativos estejam envolvidos de modo colaborativo, contribuindo, assim, com uma estreita associação entre a ação ou a resolução de um problema.
Portanto, esse desenho metodológico possibilita a utilização da pesquisa para aprimorar o ensino e a aprendizagem. O pesquisador, nesse caso, o professor, busca transformar a sua prática, ao passo que investiga, planeja e desenvolve ações, monitorando- as para avaliar os resultados.
b. Contexto e descrição dos sujeitos da pesquisa
Esta investigação foi desenvolvida em uma escola pública de Canguçu/RS, que atende aproximadamente 280 alunos distribuídos nos turnos da manhã e tarde, nas modalidades de Educação Infantil e Ensino Fundamental. A turma foi o sétimo ano “B”, onze alunos, sendo seis meninas e cinco meninos, com faixa etária entre 13 a 17 anos, e estão identificados pelas letras maiúsculas do alfabeto (A, AC, B, C, D, G, J, L, M, T e V), que correspondem às letras iniciais dos seus respectivos nomes.
Os alunos desta turma já vivenciaram a experiência de repetir de ano, pelo menos em um ano letivo e, ainda, quatro destes estão repetindo o sétimo ano pela segunda vez neste ano, portanto, estão na condição de alunos repetentes. Esses apresentam sérias dificuldades, principalmente, em relação à leitura, escrita, raciocínio e interpretação, que comprometem o ensino e a aprendizagem da Matemática e de qualquer outra área do conhecimento. Sem falar que devido a tais dificuldades o desenvolvimento de qualquer conteúdo exige um tempo maior.
Entre as características que descrevem os alunos dessa turma, podemos apontar que alguns apresentam apatia durante as aulas, falta de vontade para estudar e de compromisso com as tarefas escolares, raramente interagem com os pares e ainda pouca assiduidade às aulas. Ainda, quando questionados a respeito dos conceitos trabalhados, se compreenderam ou não, raramente pronunciam-se.
c. O F@ceMAT
A proposta de trabalho consistiu-se da criação do grupo fechado no Facebook, denominado F@ceMAT, a partir de estudos realizados, características dos alunos e das próprias considerações e observações a respeito de projetos que envolvem redes sociais. Inclusive, FELCHER, PINTO, FERREIRA (2017) defendem que um grupo fechado no Facebook, atende as características de um Ambiente Virtual de Aprendizagem (AVA). Assim, o F@ceMAT foi pensado e, portanto, utilizado para: avaliação diagnóstica; portfólio; pesquisa; construção, revisão e fixação de conceitos; repositório de material; atividade extraclasse e agenda.
Com o propósito de atender as necessidades acima mencionadas, foram desenvolvidas aproximadamente trinta (30) atividades, das quais destaca-se, mapas conceituais, vídeos, textos, imagens, desafios, jogos educativos, situações-problema, objetos de aprendizagem, criação de enquetes e eventos, entre outros, com o objetivo de reforçar conceitos trabalhados em aula, bem como suscitar a construção de outros. O conjunto de atividades propostas buscaram romper com um ensino matemático baseado ainda na maioria das vezes, na resolução de listas e listas de exercícios, logo após a explicação do professor. Tais práticas exigem além dos cálculos, a leitura, a interpretação, o raciocínio e a aplicação dos conceitos.
4. Resultados e discussões
Apostar no F@ceMAT, como espaço virtual com o objetivo de trabalhar números racionais através de inúmeras e diversificadas atividades, é evidenciar um rompimento com a prática citada por D’AMBRÓSIO (2010), comum a certas escolas, onde o ensino da Matemática se apresenta sob um viés conteudista e com uma metodologia baseada puramente no decorar e calcular, não atendendo as necessidades socioculturais do país.
Dando início ao trabalho com conteúdo programático, optou-se por começar os números racionais pelas frações, lógica sustentada por TOLEDO, TOLEDO (2009). Desse modo, as atividades no grupo F@ceMAT foram introduzidas a partir de um mapa conceitual elaborado pelos alunos sobre frações, conforme figura 1. O objetivo desse mapa foi realizar uma avaliação diagnóstica, que para HAYDT (1998) é aquela realizada no início de um curso ou período letivo com a intenção de constatar se os alunos apresentam ou não o domínio dos pré-requisitos necessários, isto é, se possuem os conhecimentos e habilidades imprescindíveis para as novas aprendizagens.
Por meio da análise dos mapas conceituais foi possível identificar a dificuldade que os alunos possuem no conceito frações, confirmando o que trazem os PCNs (1998) e também quando citam: “[...] mesmo já tendo estudado os números racionais em sua forma fracionária, ainda encontram dificuldades na resolução de exercícios com esses números” (RICKES, SILVEIRA, 2014 p. 112).
No F@ceMAT, utilizou-se uma sequência didática com o objetivo de trabalhar os números racionais, refletindo sobre cada uma das atividades propostas, seu objetivo, a relação com o que já foi e com o que ainda será trabalhado, buscando assim, ir além do que operar apenas de maneira mecânica. Atividades que priorizam a pesquisa e a investigação, levando o aluno a formular, reformular, elaborar, testar, relacionar, confrontar, comparar, entre outros. Colaborando assim para a formação de alunos pensantes, o que está em conformidade com o proposto por D’AMBRÓSIO (2010) que se refere a um ensino matemático, o qual ajude a pensar melhor e a desenvolver o raciocínio.
A respeito de um bom problema, STEWART (apud PONTE, BORCARDO, OLIVEIRA, 2013) salienta que é aquele que ao invés de conduzir a um beco sem saída, abre horizontes inteiramente novos. O interessante, desse trabalho é que resolvê-lo é apenas parte do processo, as descobertas que podem ser realizadas concomitantes ao processo por vezes são ainda mais significativas, que a própria resolução do proposto.
Duas atividades desta sequência didática serão analisadas a seguir. A primeira, em um formato de desafio, envolve operações com racionais, números opostos e formas geométricas. A segunda, um conhecido problema, Conto dos 35 camelos de Malba Tahan, que exige além de leitura, interpretação, raciocínio, compreensão de parte e todo e operações com racionais.
Assim, em relação à atividade apresentada na figura 2, a mesma deve ser dividida em 7 partes iguais, de mesmo formato, sendo que a soma dos números racionais contido em cada formato, deve ser a mesma dos demais.
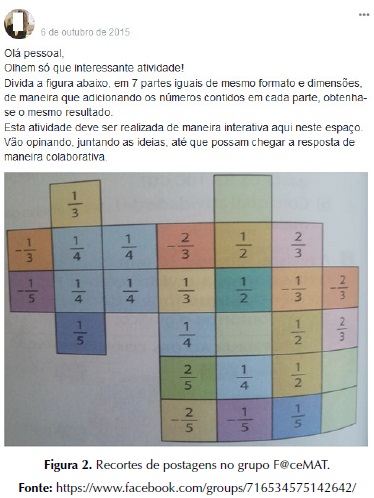
A realização da tarefa necessitou da constante interação por parte do professor. Em um primeiro momento, a aluna “A” citou que considerando 7 figuras, de mesmo formato, então, nesse âmbito cada figura teria 4 números racionais, figura 3.

Com o passar dos dias, não havendo evolução quanto ao proposto, questionados em aula a respeito da tarefa, os alunos pronunciaram-se, afirmando que não estavam conseguindo resolvê-la. No entanto, considerando que a ação educativa do professor não pode reduzi-los a tábula rasa, transformando-os em cabeças vazias, conforme DEMO (2015), retomou-se a atividade em sala de aula, figura 4, esclarecendo alguns pontos, a partir dos questionamentos apresentados por eles próprios.
Para a maioria dos alunos dessa turma, se a figura estivesse virada para cima não teria o mesmo formato da figura virada para baixo. Salientou-se, portanto, que o formato da figura independe da sua posição. Também, sugeriu-se aos alunos que realizassem uma breve pesquisa a respeito de números opostos e frações equivalentes, já que o emprego destes dois conceitos facilitaria a resolução da atividade.
PONTE, BORCARDO, OLIVEIRA (2013) referem que o sucesso de uma investigação depende da forma como ela é proposta pelo professor, do ambiente que se cria para a sua realização. É importante que o aluno sinta-se à vontade e tenha tempo para expor suas ideias, pensar, refletir, tanto com os colegas, quanto com o professor.
Afinal, o conhecimento está disponível nos mais diversos lugares, escolas, computadores, livros, bibliotecas, tornando-se cada vez mais acessível graças ao poder da informatização do conhecimento. Essa realidade vem ao encontro da necessidade de um trabalho diferenciado do professor, um trabalho muito além de repassador de informação. DEMO (2015 p. 33) cita PAPERT e GREENFIELD, ao expor que “o simples repasse não sustentará a profissão, se a ele for reduzida. Todavia, a profissão não se define mais pela transmissão, mas pela reconstrução do conhecimento, onde encontra papel insubstituível”.
Posteriormente as discussões em aula, começaram lentamente a ser postadas resoluções da atividade, como a apresentada na figura 5, que mostra o trabalho desenvolvido pelos alunos “J” e “L”.
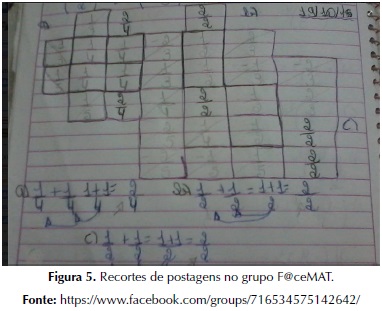
Em relação à resolução apresentada acima, figura 5, a interação acontece no sentido de questionar a respeito do formato das figuras, figura 06, porém, dando a oportunidade dos alunos refletirem e continuarem a realização do trabalho, bem como “investigar, sendo necessário deixá-lo trabalhar de forma totalmente autônoma e, como tal, o professor deve ter somente um papel de regulador da atividade” (PONTE, BROCARDO, OLIVEIRA, 2013 p. 26). Ainda, nesse contexto, DEMO (2015) ressalta a importância de o professor sair do pedestal, para apresentar-se como orientador do coletivo e de cada aluno em especial, continuará como autoridade conquistada pelo exemplo, competência e dedicação.

Na sequência, apareceram então, as primeiras resoluções em conformidade com o solicitado, figura 7. A resolução mostra que as alunas “AC” e “V” cancelaram os números opostos facilitando assim o processo de resolução, conforme indicação da professora, demonstrando saber aplicar o conceito estudado.

Além de serem postadas no F@ceMAT, as resoluções também foram discutidas em aula. Cada grupo expôs sua resolução, no sentido de ressaltar conceitos e socializar os processos empregados. Essa fase, segundo PONTE, BROCARDO, OLIVEIRA (2013) é importante para que os alunos compreendam mais sobre o que é investigar, bem como comunicar-se matematicamente e ainda, refletir sobre seu próprio trabalho e o poder de argumentação.
PONTE, BROCARDO, OLIVEIRA (2013) salientam que em se tratando de investigações matemáticas, não se sabe ao certo como iniciar, nem como concluir. No caso desta investigação, especificamente, embora todos tenham chegado ao mesmo resultado, o que é uma condição ímpar neste caso, os caminhos foram distintos, alguns mais curtos, outros mais longos. A figura 07 acima, por exemplo, traz uma resolução que empregou o conceito de números opostos, enquanto outros não utilizaram este conceito e desenvolveram um número bem maior de cálculos.
A segunda tarefa aqui em discussão é o Conto dos 35 camelos de Malba Tahan, figura 8. Os alunos em grupo tiverem a oportunidade de ler, organizar os dados, discutir, interpretar, exercendo a colaboração e interação através do espaço virtual. Para VYGOTSKY (1998 p. 17), “a colaboração entre os pares ajuda a desenvolver estratégias e habilidades gerais de solução de problemas pelo processo cognitivo implícito na interação e na comunicação”.
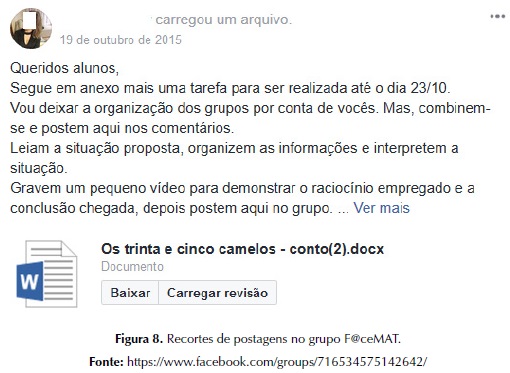
A realização dessa tarefa exigiu mais do que os alunos imaginavam e estavam acostumados a fazer. E a comum pergunta, o que eu tenho que fazer aqui não poderia ser respondida e, eles mesmos, já sabiam que não haveria uma resposta pontual e precisa para tal investigação.
No primeiro momento, como resolução do proposto, os alunos gravaram um vídeo de leitura e interpretação do conto, alunas “V” e “AC” e também “B”, “J” e “L”, quando na verdade, o solicitado era demonstrar o raciocínio empregado para se chegar na devida conclusão. Tal fato apontou para a necessidade de fazer uma retomada, fazendo-os refletirem sobre o que foi desenvolvido e “ajudá-los a fazer uma síntese da atividade, descrevendo os seus avanços e recuos, os objetivos que tinham em mente e as estratégias que seguiram”, conforme figura 9, postada no F@ ceMAT, bem como discussões e esclarecimentos em sala de aula.

Em trabalhos de pesquisa e investigação, não se sabe ao certo os caminhos que serão construídos, portanto o professor, segundo PONTE, BROCARDO, OLIVEIRA (2013) deve trabalhar com a possibilidade de imprevisibilidade, o que exigirá dele flexibilidade na condução do trabalho. Foi exatamente o que aconteceu na realização dessa tarefa, que exigiu retomada em sala de aula, novas orientações, bem como alongar o prazo de conclusão, já que a primeira versão apresentada pelos alunos não estava de acordo com o solicitado.
Ao invés de retomar as orientações da atividade em sala de aula, o professor poderia ter gravado um vídeo e postado no espaço virtual, prática relatada como bastante eficiente por BORBA, SILVA, GADANIDIS (2015). Segundo os autores, diante da dúvida de uma aluna sobre derivada e reta tangente, a doutoranda Cida Chiari gravou um vídeo, postou no YouTube e disponibilizou o link no grupo do Facebook, o que segundo a aluna sanou sua dúvida.
Assim, a realização dessa atividade investigativa considerou quatro momentos principais previstos por PONTE, BROCARDO, OLIVEIRA (2013) que são, primeiramente, o reconhecimento da situação, exploração preliminar e a formulação de questões, o segundo, por sua vez, é o processo de formulação de conjecturas, o terceiro a realização dos testes e a refinamento das conjecturas e por fim, a demonstração e avaliação do trabalho realizado. Considerando que estes momentos surgem muitas vezes simultaneamente.
O envolvimento do aluno com a aprendizagem é de fundamental importância para que os objetivos sejam alcançados, envolvimento que deve ser ainda maior em uma investigação ou pesquisa, independente da área que for. O aluno aprende quando mobiliza os seus recursos afetivos e cognitivos em prol de um objetivo (PONTE, BROCARDO, OLIVEIRA, 2013).
PONTE, BROCARDO, OLIVEIRA (2013) ressaltam a importância de quando os alunos encontram- se num impasse, com dúvidas a respeito da resolução da tarefa, o professor colocar questões abertas, conforme questionamento apresentado na figura 10. Ainda, segundo os mesmos autores, o professor também pode devolver o questionamento feito pelo aluno, para que o mesmo reflita acerca do que está sendo proposto e do que já conseguiu alcançar.
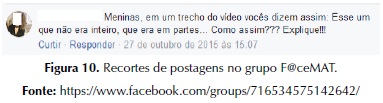
Além do que, em relação ao comentário que aparece acima, quando o professor questiona uma fala dos alunos no vídeo, onde eles dizem, “o inteiro que não era inteiro”, DEMO traz a importância de algumas insistências, entre elas:
Exercitar na formulação própria o bom uso da lógica, da argumentação, da crítica e da autocrítica, dentro da regra segundo a qual só se pode garantir o que de alguma forma tem base; não adianta construir algo que ninguém mais pode decifrar, ou usar linguagem particular inacessível, ou complicar por complicar etc. (2015 p. 40)
Mesmo após as explicações, em sala de aula e no grupo, e as interações ocorridas, o segundo vídeo de alguns grupos não apresentou exatamente o esperado pelo professor. No entanto, “não conseguindo resolver o problema, o trabalho não deixa de valer a pena pelas descobertas imprevistas que o proporciona” (PONTE, BROCARDO, OLIVEIRA, 2013 p. 17).
A partir de então, considerando que o trabalho foi importante para desenvolver o pensar dos alunos, pois, estes trabalharam com a formulação de conjecturas, falhando no momento de refiná-las, optou-se por aceitar a segunda versão dos vídeos e, então, em sala de aula, discutir o raciocínio que fora empregado para resolver o problema dos 35 camelos.
Os alunos “A”, “AC” e “V” conseguiram efetuar corretamente os cálculos, apresentando que a soma das frações 1/2 + 1/3 + 1/9 = 17/18 e que essa fração equivale a 34/36, de acordo com a figura 11. No entanto, muitos não deixaram claro nos seus vídeos que o denominador 36 corresponde aos 35 camelos da herança, mais o camelo que foi adicionado pelo homem que calculava e, que 34 corresponde aos camelos que os três filhos receberam pela herança. Assim 36 – 34 = 2, corresponde aos dois camelos que o homem que calculava recebeu, um que ele mesmo havia colocado na divisão e o outro que resolvido o impasse.
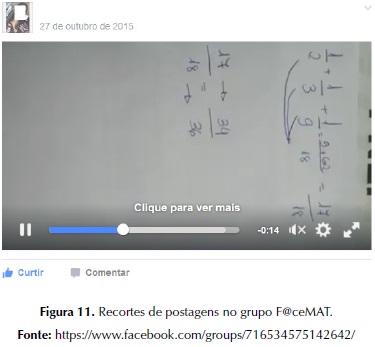
Outro ponto que não ficou claramente expresso nos vídeos se refere ao fato de os irmãos terem recebido mais do que imaginavam e, mesmo assim ter, sobrado um camelo. Em nenhum dos vídeos é mencionado que isso se deve ao fato de que as três frações somadas não correspondem a um inteiro, portanto, 17/18.
A respeito da avaliação de uma investigação, PONTE, BROCARDO, OLIVEIRA (2013) falam da importância das apresentações orais, quando alunos relatam aos professores e demais colegas o que foi produzido no percurso. Nesse caso, esta sugestão foi considerada, porém, em um formato de vídeo e, posteriormente, postagem no grupo.
É evidente que as tecnologias presentes em nosso dia a dia armazenam informações e nos apresentam, muitas vezes, de maneira bastante atrativa e de fácil acesso, o que nos faz refletir sobre aula copiada, fórmulas simplesmente aplicadas sem entendimentos e também listas de exercícios resolvidos, sem compreensão, puro treinamento. Para DEMO (2015) essa prática que certos professores de matemática desenvolvem com seus alunos é uma extensão do que fizeram com eles. Profissionais estes, resultado de um processo de domínio de conteúdos, sem qualquer questionamento reconstrutivo.
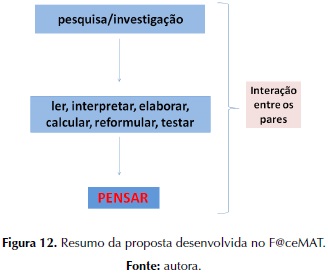
DEMO (2015 p. 20) cita que “a sala de aula clássica precisa ser repensada”. Portanto, sugere-se que a pesquisa e a investigação sejam práticas cotidianas, desenvolvidas através da leitura, interpretação, elaboração, cálculo, reformulação, testes, entre outros, buscando, assim, desenvolver o pensar. Sem esquecer que a interação entre os pares é imprescindível neste processo, conforme aponta figura 12.
A respeito do trabalho que a escola deveria fazer, pontua que: “nela nada se repassa mecanicamente. Antes, tudo precisa virar saber pensar” (DEMO, 2015 p. 30). Para D’AMBRÓSIO (2010), o rápido avanço que se presencia faz com que não se saiba como será o futuro e, portanto, o que será exigido, o que precisará saber. À vista disso, para ele, quem souber pensar, com certeza estará preparado para enfrentar os desafios impostos por um amanhã incerto.
Até então, segundo ALARCÃO (2011), ser aluno é ser aprendente. Aprender ao longo da vida. O que não é contemplado, nem estimulado com práticas que se resumem a decoreba e treinamento. Por isso, ressalta-se e enfatiza-se a pesquisa e a investigação como práticas cotidianas que estimulam o pensar e, portanto, aprender continuamente.
5. Considerações finais
Esta investigação teve por base a preocupação pela escolha do conteúdo curricular números racionais, estudado pelos alunos na escola, porém, sabe-se que muitos saem do ensino formal sem o real entendimento do que é uma fração, dificuldade que muitas vezes se alastra até o Ensino Superior. Em se tratando da perspectiva de ensino desse e de outros conteúdos curriculares, muitos são concebidos como inquestionáveis, verdades absolutas, trabalhados através de metodologias, que se resumem a copiar e resolver listas de exercícios.
Nesse sentido, acredita-se que muitas das dificuldades em relação ao entendimento do conteúdo curricular aqui em discussão são justificados pelas práticas de colorir figuras, operar com frações sem sentido, desvinculadas da realidade, metodologias comuns e ineficientes do ponto de vista da aprendizagem.
A escolha da turma também foi um desafio, pequena, mas repleta de dificuldades e adversidades, visivelmente merecedora de atenção. Portanto, conteúdo que muitos alunos apresentam dificuldade, turma “problema” e uma rede social, considerada por muitos como espaço para diversão e bate-papo com amigos, formaram o tripé para desenvolver o pensar, que foi o que se buscou nesse espaço e com estes alunos, usando como aporte o conteúdo citado.
Em suma, esse espaço virtual oportunizou o ensino e a aprendizagem dos números racionais de maneira diferenciada, utilizando o Facebook para troca, aprofundamento, construções, entre outros, partindo de propostas diversificadas, como foi analisado. Assim, esses alunos, considerados apáticos, pouco questionadores e participativos, demonstram- -se diferentes, a realidade foi modificando-se e aos poucos foram envolvendo-se com as atividades e aumentando a participação, que até então estava relacionada a cobrança do professor.
Ainda, sem deixar de mencionar que, em sala de aula, também a realidade foi se modificando e, expressões como “não sei fazer” foram dando espaço às expressões como “eu vou tentar”, “é assim?”. Enfatiza-se que independente da metodologia adotada pelo professor, a dedicação do aluno, que geralmente está atrelada as propostas que lhe são apresentadas, é de suma importância nos processos de ensino e aprendizagem, sendo condição fundamental para a construção do conhecimento.
Por fim, pontua-se como positiva essa investigação considerando o objetivo que se propôs, pois possibilitou aos alunos aprender mais sobre os números racionais e desenvolver o pensar por meio de atividades de pesquisa e investigação, contribuindo para modificar o paradigma tradicional de ensino da Matemática.
Referências Bibliográficas
ALARCÃO, I. Professores reflexivos em uma escola reflexiva. Cortez, São Paulo, Brasil. 2011.
BRASIL. Parâmetros Curriculares Nacionais: Matemática. MEC, Brasília, Brasil. 1998.
BRASIL. Lei de Diretrizes e Bases da educação Nacional. LDB 9394/96. Disponível em: http:// www.planalto.gov.br/ccivil_03/Leis/L9394.htm. Acesso em: 02 set. 2015.
BORBA, M. C.; SILVA, R.S. R.; GADANIDIS, G. Fases das tecnologias digitais em Educação Matemática. Autêntica, Belo Horizonte, Brasil. 2015.
COSTA, M. V. (org). A escola tem futuro? DP&A, Rio de Janeiro, Brasil. 2003.
D’AMBRÓSIO. U. Educação Matemática: da Teoria à prática. 19 ed. Papirus, Campinas, SP, Brasil. 2010.
DEMO, P. Metodologia da Investigação em Educação. Ibpex, Curitiba, Brasil. 2005.
DEMO, P. Educar pela pesquisa. Editora Autores Associados, Campinas, Brasil. 2015.
FELCHER, C. D. O; PINTO, A. C.; FERREIRA, A. L. A. O uso do Facebook como Ambiente Virtual de Aprendizagem para o ensino dos números racionais. Revista Paranaense de Educação Matemática, v. 6, n. 10, pp. 246-271. 2017.
GIL, A. C. Métodos e Técnicas de Pesquisa Social. 6 ed. Atlas, São Paulo, Brasil. 2012.
GOMES, M. L. M. História do ensino da Matemática: uma introdução. CEAD-UFMG, Belo Horizonte, Brasil. 2012.
GONZÁLES, J, ARRIECHE, M. Significados Institucionales y Personales de lãs Fracciones em Educación Básica. In: Acta Latino Americana de Matemática Educativa. v. 18. México. 2005.
HAYDT, R. C. C. Avaliação do processo ensino- -aprendizagem. Ática, São Paulo, Brasil. 1998.
IRWIN, C. K. Using Everyday Knowledge of Decimals to Enhance Understanding. Journal for Research in Mathematics Education. Auckland, v. 32, n. 4, pp. 399-420. 2001.
LOPES, A. J. O que os Nossos Alunos Podem Estar Deixando de Aprender sobre Frações, quando Tentamos Ensinar Frações. Revista Bolema, Rio Claro, SP, n. 31, pp. 1-22. 2008.
MARANHÃO, M. C; IGLIORI, S. B. C. Registros de representação e números racionais. In: MACHADO, S. D. A. Aprendizagem em matemática - registros de representação semiótica. Papirus, São Paulo, Brasil. 2003, pp. 57-70.
MENEGHETTI, R. C. G; NUNES, A. C. A. Aplicação de uma proposta pedagógica no ensino dos números racionais. Educação Matemática em Revista, n. 20-21, pp. 77- 86, 2006.
PRIMO, A. Interação mediada por computador. Sulina, Porto Alegre, Brasil. 2011.
PONTE, J. P.; BROCARDO, J.; OLIVEIRA, H. Investigações Matemáticas na Sala de Aula. 3 ed. Autêntica, Belo Horizonte, Brasil. 2013.
RICKES, J., SILVEIRA, D. Material concreto manuseável: um motivador para o ensino de frações. In.: FONSECA, M.S. et al. (org). Matemáticas: educação e pesquisa. Ed. Da Universidade Federal de Pelotas, Pelotas, Brasil. 2014. pp. 106-123.
SELBACH, S. Matemática e didática. Vozes, Petrópolis, Brasil. 2010.
THIOLLENT, M. A metodologia da pesquisa-ação. Cortez, São Paulo, Brasil. 2011.
TOLEDO, M.; TOLEDO, M. Teoria e prática de Matemática: como dois e dois. FTD, São Paulo, Brasil. 2009.
TRIPP, D. Pesquisa-ação: uma introdução metodológica. Revista Educação e Pesquisa, São Paulo, v. 31, n. 3, pp. 443-466, set./dez. 2005. Disponível em: <http://www.scielo.br/pdf/ep/v31n3/ a09v31n3.pdf. Acesso em: 01/12/2014.
VYGOTSKY, L. A formação social da mente: o desenvolvimento dos processos psicológicos superiores. Martins Fontes, São Paulo, Brasil. 1998.
Licencia
Góndola, Ens Aprend Cienc. es una publicación de acceso abierto, sin cargos económicos para autores ni lectores. La publicación, consulta o descarga de los contenidos de la revista no genera costo alguno para los autores ni los lectores, toda vez que la Universidad Distrital Francisco José de Caldas asume los gastos relacionados con edición, gestión y publicación. Los pares evaluadores no reciben retribución económica alguna por su valiosa contribución. Se entiende el trabajo de todos los actores mencionados anteriormente como un aporte al fortalecimiento y crecimiento de la comunidad investigadora en el campo de la Enseñanza de las Ciencias.
A partir del 01 de diciembre de 2018 los contenidos de la revista se publican bajo los términos de la Licencia Creative Commons Atribución–No comercial–Compartir igual 4.0 Internacional (CC-BY-NC-SA 4.0), bajo la cual otros podrán distribuir, remezclar, retocar, y crear a partir de la obra de modo no comercial, siempre y cuando den crédito y licencien sus nuevas creaciones bajo las mismas condiciones.
Los titulares de los derechos de autor son los autores y la revista Góndola, Ens Aprend Cienc. Los titulares conservan todos los derechos sin restricciones, respetando los términos de la licencia en cuanto a la consulta, descarga y distribución del material.
Cuando la obra o alguno de sus elementos se halle en el dominio público según la ley vigente aplicable, esta situación no quedará afectada por la licencia.
Asimismo, incentivamos a los autores a depositar sus contribuciones en otros repositorios institucionales y temáticos, con la certeza de que la cultura y el conocimiento es un bien de todos y para todos.





















