DOI:
https://doi.org/10.14483/23464712.10491Published:
2017-07-07Representaciones semióticas alrededor del concepto de función en estudiantes de ingeniería
Semiotic representations around the concept of function in engineering students
Keywords:
articulation of registers, function, algebraic register, graphic record, semiotic representations (en).Keywords:
articulación de registros, función, registro algebraico, registro gráfico, representaciones semióticas (es).Downloads
References
ARTIGUE, M. La enseñanza de los principios del cálculo: problemas epistemológicos, cognitivos y didácticos. In: ARTIGUE, M.; DOUADY, R.; MORENO, L. y GÓMEZ, P. (eds.), Ingeniería didáctica en educación matemática. Grupo Editorial Iberoamericano. Ciudad de México: México, 1995. pp. 97-140.
JAIMES, L. A.; CHAVES, R. F.; HERNÁNDEZ, C. A. Planteamiento de una ecuación diferencial lineal de primer orden que modela un problema de mezclas: Una dificultad en la movilización entre registros de representación, lengua natural y algebraico. Elementos, 5(5), 23-31. 2015.
BORBÓN, A. Concepciones de profesores sobre varios conceptos del cálculo diferencial. Centro de Investigación y de Estudios Avanzados del IPN. Ciudad de México: México, 2003.
GONZÁLEZ-MARTÍN, A. y CAMACHO, M. Legitimization of the Graphic Register in University Teaching. The Case of the Improper Integral. In: HOINES M. J. y FUGLESTAD A. B. (eds.) Proceedings of the 28th International Conference for the Psychology of Mathematics Education, 2 ed., Bergen: Noruega, 2004. pp. 479-486.
D’AMORE, B. Objetos, significados, representaciones semióticas y sentido. Revista latinoamericana de investigación en matemática educativa (RELIME), 9(1), 177-196. 2006.
DUVAL, R. Registres de représentation sémiotique et fonctionnement cognitif de la pensée. Annales de Didactique et de Sciences Cognitives, 5, 37-65. 1993.
DUVAL, R. Registros de representación semiótica y funcionamiento cognitivo del pensamiento. In: HITT, F. (ed.), Investigaciones en Matemática Educativa II. Grupo Editorial Iberoamericano. Ciudad de México: México, 1998. pp. 173-201.
FONT, V.; GODINO, J.; D’AMORE, B. Enfoque ontosemiótico de las representaciones en educación matemática. For the Learning of Mathematics, 27(2), 3-9. 2007.
GARCÍA, L.; VÁSQUEZ, R.; HINOJOSA, M. Dificultades en el concepto de función en estudiantes de ingeniería. Revista Latinoamericana de Investigación en Matemática Educativa, 7(24), 27-34. 2004.
GUTIÉRREZ, S. I. Caracterización de tratamientos y conversiones: el caso de la función afín en el marco de las aplicaciones. Universidad Pedagógica Nacional. Bogotá D.C: Colombia, 2007.
GUZMÁN, I. Registros en juego en el concepto de función, comportamiento de una muestra de estudiantes chilenos. XVII Semana de la Matemática de la Universidad Católica de Valparaíso. Universidad Católica de Valparaíso. Valparaíso. 1990.
GUZMÁN, I. Registros de representación, el aprendizaje de nociones relativas a funciones: voces de estudiantes. Revista latinoamericana de investigación en matemática educativa (RELIME), 1(1), 5-21. 1998.
HITT, F. Funciones en contexto. Proyecto sobre visualización matemática. Departamento de Matemática Educativa Cinvestav. Ciudad de México: México, 2000.
IBARRA, S.; BRAVO, J.; GRIJALVA, A. El papel de los registros de representación semiótica en la enseñanza del cálculo diferencial. XII Semana de Investigación y Docencia en Matemáticas (pp. 107-114). Departamento de Matemáticas. Universidad de Sonora. Hermosillo, México. Recuperado de: http://semana.mat.uson.mx/ MemoriasXVII/XII/IbarraOlmos.pdf. 2002.
NÁPOLES, J.; GONZÁLEZ, T.; GENES, F.; BASABILBASO, F.; BRUNDO, J. El enfoque histórico problémico en la enseñanza de la matemática para ciencias técnicas: el caso de las ecuaciones diferenciales ordinarias. Acta Scientiae, 6, 41-59. 2004.
PLANCHART, O. La visualización y la modelación en la adquisición del concepto de función. Universidad Autónoma del Estado de Morelos. Cuernavaca, México. Recuperado de: http://ponce.inter.edu/cai/tesis/oplanchart/inicio. Pdf. 2002.
RICO, L. Sobre las nociones de representación y comprensión en la investigación en educación matemática. PNA, 4(1), 1-14. 2009.
VÁSQUEZ, S. El concepto de función a través de la historia. Revista Iberoamericana de Educación (Unión), 1(16), 141-155. 2008.
How to Cite
APA
ACM
ACS
ABNT
Chicago
Harvard
IEEE
MLA
Turabian
Vancouver
Download Citation
DOI: 10.14483/udistrital.jour.gdla.2017.v12n2.10491
REPRESENTACIONES SEMIÓTICAS ALREDEDOR DEL CONCEPTO DE FUNCIÓN EN ESTUDIANTES DE INGENIERÍA
Semiotic representations around the concept of function in engineering students
Raúl Prada Núñez1
César Augusto Hernández Suárez2
Luis Alberto Jaimes Contreras3
Cómo citar este artículo: Prada, R., Hernández, C.A., Jaimes L.A. (2017). Representaciones semióticas alrededor del concepto de función en estudiantes de ingeniería. Góndola, Enseñ Aprend Cienc, 12(2), 14-25. doi: 10.14483/udistrital.jour.gdla.2017.v12n2.a1.
Recibido: 30 de mayo 2016 / Aceptado: 9 de diciembre de 2016
1 Magíster en Educación Matemática. Docente Tiempo Completo Universidad Francisco de Paula Santander, Colombia. Correo electrónico: raulprada@ufps.edu.co
2 Director Licenciatura en Matemáticas. Director Grupo de Investigación en Pedagogía y Practicas Pedagógicas - GIPEPP. Docente Departamento de Pedagogía, Andragogía, Comunicación y Multimedios. Universidad Francisco de Paula de Santander. Correo electrónico: cesaraugusto@ufps.edu.co
3 Magíster en Docencia de la Matemática. Docente Escuela Colombiana de Ingeniería Julio Garavito, Colombia. Correo electrónico: luis.jaimes@escuelaing.edu.co
Resumen
Este artículo retoma parte de una investigación cuyo objeto de estudio son las representaciones semióticas en la enseñanza alrededor del concepto de función en el cálculo diferencial. Tiene como objetivo analizar las representaciones semióticas a partir de la preferencia en los tipos de registro que adoptan los estudiantes alrededor del concepto de función en las carreras de ingeniería, específicamente, en la asignatura Cálculo Diferencial. Se toman como marco de referencia los trabajos de DUVAL (1993, 1998) y HITT (2000), los cuales evidencian favorabilidad derivada de la articulación coherente de los diversos registros de representación semiótica en los procesos de enseñanza (registro algebraico, registro gráfico, registro tabular, entre otros). La investigación se enmarca dentro de un diseño cuasi-experimental y nivel explicativo descriptivo. En los resultados encontrados se identificó que los estudiantes ingresan a la educación superior con bajo nivel conceptual de precálculo, lo que dificulta la comprensión de nuevos conceptos. Por otra parte, se evidencia que persiste el modelo de enseñanza tradicional en el cual, como se ha mencionado en diferentes investigaciones, predomina el registro algebraico sobre otros registros de representación, lo que, en el momento de resolver problemas rutinarios y no rutinarios, dificulta al estudiante la búsqueda de soluciones acertadas. Se destaca que la articulación de los diversos registros de representación permite validar la teoría de DUVAL (1998), reafirmando que en la comprensión de los conceptos matemáticos no debe hacerse de manera directa, como en otras áreas, por lo que es necesario emplear distintas formas de representación y establecer una correcta conexión e intervinculación con el fin de garantizar el aprendizaje en los estudiantes.
Palabras clave: articulación de registros, función, registro algebraico, registro gráfico, representaciones semióticas.
Abstract
This paper takes into account part of a research whose object of study is semiotic representations in teaching concept of function. It aims to analyze semiotic representations based on preference in types of record that students adopt around the concept of function in engineering careers, specifically, in the subject Differential Calculus. We take as a frame of reference the proposals by Duval (1993, 1998) and Hitt (2000), which showing favorability derived from coherent articulation between various registers of semiotic representation in teaching (algebraic registration, graphic record, tabulate registration, among others). This research is a quasi-experimental design in a descriptive explanatory level. Results let us to identify that students enter higher education have low pre-calculus conceptual level, making it difficult to acquire new concepts. It is evident that traditional model of education persists; in which, as mentioned in different researches, algebraic registration predominates over other representation registers, whose consequence is that when solving routine and no routine problems, students can not find successful solutions. We emphasize that articulation between different representation registers allow us to validate the theory of Duval (1998), reaffirming that mathematical concepts, unlike the inherent concepts of many disciplines, cannot be addressed directly, so shapes that represent them are required and correct articulation of them allows students to appropriate the concepts.
Keywords: articulation of registers, function, algebraic register, graphic record, semiotic representations.
Desde las prácticas educativas e investigativas en el campo de la educación matemática, se evidencia que un considerable número de estudiantes que inician pregrado en programas de ingeniería no alcanzan los objetivos esperados en cursos iniciales de matemáticas. Este bajo rendimiento académico genera problemas como la repitencia y deserción académica.
Uno de los problemas que deben enfrentar los docentes a diario en su labor de aula es el considerable porcentaje de estudiantes que presentan dificultades en el proceso de comprensión y apropiación de los conceptos matemáticos. Esta situación se refleja en los malos resultados que obtienen los estudiantes en pruebas de carácter interno, regional o nacional, y que al final coinciden con los índices de pérdida, repitencia y deserción académica.
El objeto de estudio es el concepto de función y se espera identificar cómo la articulación coherente de diversos registros de representación facilita el entendimiento de dicho concepto, el cual se considera esencial para la comprensión de conceptos más complejos y es uno de los ejes fundamentales en los cursos de cálculo universitario.
Investigadores han evidenciado que desde la experiencia docente se observa que los estudiantes después de enfrentarse al concepto de función, se limitan al uso de una regla para probar cuándo una relación lo es. Es decir, lo validan de forma algebraica limitando su comprensión, ya que es necesario que el estudiante se apropie del concepto en todas sus formas de representación para que pueda entenderlo plenamente (PLANCHART, 2002; ARTIGUE, 1995).
Algunos estudios que proponen cambios en el modelo de enseñanza tradicional afirman que “Actualmente predomina el enfoque algebraico como reflejo de la primera forma para resolver problemas… y que algunos docentes hoy en día emplean como estrategia didáctica” (JAIMES, CHÁVES y HERNÁNDEZ, 2015 p. 24). En consecuencia, es frecuente encontrar en la enseñanza del cálculo que algunos conceptos sean evadidos y ocultados con fórmulas o algoritmos, lo que impide la comprensión precisa del concepto y puede llevar incluso, tanto a estudiantes como a docentes, a concebir una fórmula como un concepto en sí mismo (NÁPOLES, GONZÁLEZ, GENES, BASABILBASO y BRUNDO, 2004). Las citas anteriores revelan que el proceso pedagógico que se practica en el aula es uno de los factores de mayor incidencia en la comprensión de conceptos matemáticos, pero ¿qué estrategias de enseñanza pueden mejorar la compresión de conceptos matemáticos?
Para dar respuesta a esta pregunta se toma como referencia la teoría de las representaciones semióticas (DUVAL, 1993, 1998). Este enfoque teórico afirma que un concepto se construye mediante tareas que impliquen el uso de diferentes sistemas de representación y promuevan la articulación coherente entre sus representaciones. Otros autores, como HITT (2000), mencionan que el conocimiento de un individuo sobre un concepto es estable si es capaz de articular diferentes representaciones, libres de contradicciones, de este.
Análogamente a lo que ocurre con la enseñanza de otros conceptos y definiciones matemáticas se debe innovar con distintas estrategias didácticas que, al ser empleadas por el docente, permitan realizar distintas representaciones, de manera que el estudiante pueda captar y dominar en toda su dimensión los conceptos expuestos (DUVAL, 1998); GUZMÁN, 1990, 1998; IBARRA, BRAVO y GRIJALVA, 2002). En particular, DUVAL sostiene que:
Las diferentes representaciones semióticas de un objeto matemático son absolutamente necesarias, ya que los objetos matemáticos no son directamente accesibles por la percepción o por una experiencia intuitiva inmediata como lo son los objetos comúnmente llamados físicos. (DUVAL, 1998 p. 182)
En relación con lo anterior, queda clara la existencia de dificultades en el proceso de enseñanza- aprendizaje de los estudiantes de distintos niveles de escolaridad alrededor del concepto de función, esto como consecuencia de la aplicación de un sistema tradicional de enseñanza que ha favorecido la utilización de unos registros más que otros. Se ha evidenciado cómo las representaciones semióticas de este concepto matemático se han presentado a los estudiantes de forma desarticulada, lo cual ha generado dificultades en la comprensión del concepto matemático, ya que posteriormente le es difícil al estudiante unificar sus diferentes representaciones para dar un significado integral. Alrededor de este tema se han desarrollado innumerables investigaciones, por ejemplo, las investigaciones producto de tesis de maestría y doctorado (GUTIÉRREZ, 2007; PLANCHART, 2002; VÁSQUEZ, 2008) o los estudios desarrollados por investigadores reconocidos como ARTIGUE (1995), DUVAL (1998), HITT (2000), D’AMORE (2006) entre otros.
No obstante, el presente estudio busca analizar las representaciones semióticas a partir de la preferencia en los tipos de registro que adoptan los estudiantes alrededor del concepto de función. En este sentido, la presente investigación pretende dar respuesta a las siguientes preguntas: ¿cuál es la preferencia de los docentes a la hora de articular diferentes registros de representación semiótica en el proceso de enseñanza del tema de funciones a estudiantes de ingeniería? y ¿de qué forma utilizan los estudiantes las distintas representaciones semióticas en el aprendizaje del concepto de función?
Método
La investigación se enmarca dentro de un diseño cuasi-experimental, ya que se busca controlar la mayor cantidad de variables influyentes (edad, género, estado civil, conocimientos previos, horarios de clase, salones de trabajo, entre otras) con el fin de aislar la variable “rendimiento académico” y que en mayor medida quede influenciada por la variable “metodología de enseñanza”. Así mismo, el nivel de la investigación es explicativa-descriptiva, pues se busca captar todos los posibles efectos en los estudiantes que se puedan derivar de la implementación de las metodologías.
La muestra del estudio se conformó con los estudiantes de primer semestre de la Facultad de Ingeniería de la Universidad Francisco de Paula Santander (UFPS), en la ciudad de Cúcuta (Colombia), matriculados para el primer semestre de 2015 en la asignatura Cálculo Diferencial en los programas de Ingeniería de Sistemas (grupo A), Ingeniería Electromecánica (grupo B) e Ingeniería Electrónica (grupo C). Se aplicó un proceso de muestreo no probabilístico utilizando la técnica de muestreo por conveniencia, pues la intención era identificar la posible existencia de diferencias académicas entre los estudiantes que ingresan a los diferentes programas curriculares de la Facultad de Ingeniería. Los estudiantes en el curso de Ingeniería de Sistemas fueron 42 y en los cursos de Ingeniería Electromecánica y Electrónica hubo 41 estudiantes. Ambos grupos están integrados por estudiantes de ambos sexos, con predominio del masculino, y edad promedio de 17 años, se destaca que aproximadamente el 95% de ellos se graduaron del colegio (educación media) en el año 2014 y provienen de familias cuyo estrato socioeconómico corresponde a niveles 2 y 3.
En este proceso investigativo se aplicaron dos cuestionarios, uno al comienzo de semestre y antes de iniciar el trabajo con cada grupo con el fin de determinar las características demográficas (edad, género, estado civil, tipo de institución educativa en la que se graduó, año en que se graduó, estrato socio-económico, entre otros aspectos) y académicas (conocimientos básicos en aritmética y en álgebra) de cada grupo. Esta prueba fue denominada pretest (anexo A). Posteriormente, se aplicó una segunda prueba con la intensión de medir el nivel de conceptualización de los estudiantes en cada grupo después del proceso de intervención metodológica, es decir, la prueba postest (anexo B). El énfasis del análisis de los registros semánticos (algebraico y gráfico) se hizo sobre la base de las respuestas de los ítems 5 y 6 de estas pruebas. En el desarrollo de la presente investigación se ejecutaron varias etapas:
Primero, se procedió a determinar de los siete programas que posee la Facultad de Ingenierías de la UFPS aquellos con las tasas más altas de repitencia. Fueron elegidos los programas de Ingeniería de Sistemas, Electromecánica y Electrónica.
Segundo, se tomó la decisión de recolectar los datos con los grupos de la asignatura Cálculo Diferencial de cada uno de los programas elegidos, debido a que en estos grupos solo están matriculados estudiantes que ingresan por primera vez a la educación superior y no hay presencia de repitentes, los cuales podrían poseer algún tipo de sesgo.
Tercero, una vez definidos los programas y el curso a trabajar, se tuvo contacto con los directores de cada programa con el fin de lograr sincronizar horas y días de clase, complementándolo con que las clases fueran en el mismo edificio y mismo piso. Solo de esta forma se podría garantizar que las condiciones ambientales de los tres grupos fueran similares. Esto se hace con el fin de reducir el efecto del mayor número de factores que puedan producir ruido en los resultados.
Cuarto, se realizó una selección de los docentes que trabajarían en el proyecto, los cuales debían cumplir dos características: por un lado, debían ser docentes de este curso con una misma formación profesional (en este caso, licenciados) y, adicionalmente, debían tener experiencia en esta asignatura de mínimo dos años. Una vez seleccionados los docentes, se les informó de los objetivos de la investigación y cada uno eligió una de las estrategias de enseñanza a implementar. Como actividad complementaria, cada docente junto con el investigador, y apoyados en su experiencia docente, textos guía y material de apoyo, procedió a realizar cada una de las actividades a desarrollar en clase.
Quinto, se realizó la asignación de grupos y de estrategias a utilizar. Para ello, y con el fin de garantizar la aleatoriedad, se generaron dos listas (una con los programas académicos y la otra con la metodología a implementar), posteriormente fueron introducidos los elementos de cada lista en bolsas independientes. Se procedió a sacar un papel de cada bolsa y de esa forma se obtuvieron tres parejas con las características de trabajo. Los resultados de este sorteo se muestran en la tabla 1.
Sexto, una vez organizados los grupos, las metodologías y los docentes se procedió a tratar los temas definidos, utilizando en el aula el aprendizaje cooperativo. Actividad que se desarrolló así: al inicio de la clase el docente propone el objetivo de trabajo junto con el tema a tratar, posteriormente, los estudiantes conforman grupos de tres personas y cada grupo comienza a desarrollar la actividad. La intención es que los estudiantes manifiesten sus concepciones dentro de su grupo, las discutan con sus compañeros hasta llegar a un punto en común, si es necesario el docente interviene en el proceso (pero no para resolver el problema, sino para re-orientar la discusión). Pasados aproximadamente noventa minutos se procede a socializar pregunta a pregunta en el tablero con la participación de los todos los grupos. Esta socialización la coordina el docente, apoyado en las herramientas que le ofrece la metodología correspondiente, con la intención de afinar conceptos. El proceso se repite tema tras tema, en los casos en que fue necesario se extendió uno o más minutos la proyección con el fin de garantizar la claridad de conceptos en el grupo.
Resultados
Los resultados de la investigación se mostrarán en función de las pruebas aplicadas en la investigación, iniciando con los resultados del pretest y luego del postest.
De la prueba pretest se desprenden dos tipos de información. En primer lugar, las características sociodemográficas de los grupos: en todos los grupos el porcentaje de mujeres no supera el 10%, se graduaron en el 2014 de colegios públicos con énfasis académico o técnico, sus edades oscilan entre 16 y 19 años, solteros residentes en Cúcuta y su área metropolitana, pertenecientes a los estratos socio-económicos 2 y 3.

Para la evaluación de las representaciones semióticas en esta fase se analizaron los ítems que hacen referencia específica a la articulación algebraico y gráfico y su conjunción alrededor de la representación semiótica del concepto de función. Los resultados se muestran en las figuras 1A y 1B para el pretest. Los análisis graficados en la figura 1A muestran los estudiantes a quienes se les proporcionó una función constante definida en forma algebraica utilizando lenguaje formal matemático y a quienes se hicieron cuestionamientos relacionados con elementos que integran el dominio, el rango y puntos sobre la trayectoria de la gráfica.
En esta imagen se evidencia en todos los grupos un alto porcentaje de desaciertos en las respuestas (entre 30 y 40%), siendo más altos en el grupo C, así como cierta similitud en los porcentajes de acierto (alrededor de 55%). Estos resultados se complementan con los altos porcentajes de estudiantes que no respondieron a las preguntas planteadas (20% en el grupo A), lo cual podría deberse a la rigurosidad del lenguaje matemático en que se realizó el ejercicio, pese a que se trataba de una función sencilla como lo es la función constante.
La figura 1B refleja los resultados del ejercicio en el que se le proporcionó al estudiante una función definida por tramos en el registro gráfico. A partir de ella debía identificar parejas ordenadas que pertenecían a la función. Se puede observar que en los grupos donde se aplicaron las metodologías B y C aproximadamente el 35% de los estudiantes escribieron correctamente las ecuaciones que representan cada segmento de la función, tomando como punto de partida la representación gráfica de la misma. Cabe resaltar que en la metodología B los estudiantes que están en la categoría de incorrecto (menos del 40%) escribieron bien las ecuaciones de los primeros dos segmentos de la función y que en el grupo de la metodología tradicional (grupo C) fue donde se presentó el porcentaje más alto de “no responde”, alcanzando aproximadamente el 20%. Es importante señalar que el nivel de rendimiento de los estudiantes del grupo de la metodología B se debió a que el ejercicio se planteó a partir de la representación gráfica.
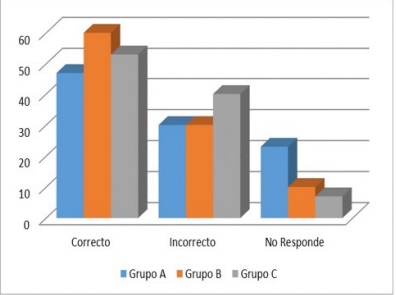
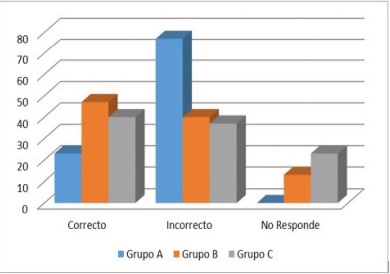
Figura 1. A) Función definida en forma algebraica, B) Función definida en forma gráfica.
Fuente: elaboración propia de los autores.
En resumen, en la fase del pretest se observó en todos los grupos dificultad para identificar las características que poseen los diversos conjuntos numéricos, escaso dominio de las operaciones básicas entre ellos, dificultades para diferenciar y resolver ecuaciones e inecuaciones, y un escaso dominio sobre temas de álgebra tales como productos notables y casos de factorización. Por otra parte, se encontró que los estudiantes no entienden el concepto de par ordenado, lo que dificulta su respectiva ubicación en el plano y, en consecuencia, todos los temas que se deriven de su aplicación. En toda la prueba se evidencia un índice de no respuesta que alcanza en promedio el 50%, aspecto que evidencia las posibles dificultades que pueden tener los estudiantes al inicio de este curso, ya que se supone que los conceptos evaluados son los que deberían dominar en el momento de recibir el título de bachiller, según los estándares curriculares establecidos por el Ministerio de Educación Nacional.
Las respuestas a los ítems que hacen referencia específica a la articulación algebraico y gráfico y su conjunción alrededor de la representación semiótica del concepto de función en la fase de postest se muestran en las tablas 2 y 3. La tabla 2 muestra un resumen de las respuestas de los estudiantes ante una función constante definida en forma algebraica utilizando lenguaje formal matemático. Posteriormente, se les cuestionó respecto a elementos que integran el dominio, el rango y puntos sobre la trayectoria de la gráfica.
En la tabla 3 se ilustra el resumen de las respuestas de los estudiantes ante una función definida por tramos en el registro gráfico. A partir de ella, debían identificar parejas ordenadas que pertenecían a la función.
En general, en la evaluación a través de la prueba del postest, se evidencian mejoras en todos los grupos, se destaca que en el momento de definir función los estudiantes utilizan elementos de lenguaje formal de las matemáticas para proporcionar conceptos más técnicos. También muestran un mayor uso de los diversos registros de representación, aunque es el pasaje del registro gráfico al algebraico el que sigue ofreciendo mayores dificultades con los estudiantes de metodologías tradicionales. Los estudiantes de los grupos B y C mostraron una mejor apropiación de los conceptos trabajados, en consecuencia, hubo una disminución del índice de no respuesta en toda la prueba (menos del 10% de la totalidad de ítems del cuestionario) y, así mismo, se observó en los grupos una mejor actitud al momento de resolver problemas y ejercicios. Por último, se observó un mayor compromiso por parte de los estudiantes en plasmar en la prueba lo que sabían, lo que entendían o recordaban, esto se evidenció en el uso de un mayor número de herramientas de apoyo en el momento de analizar las situaciones propuestas.
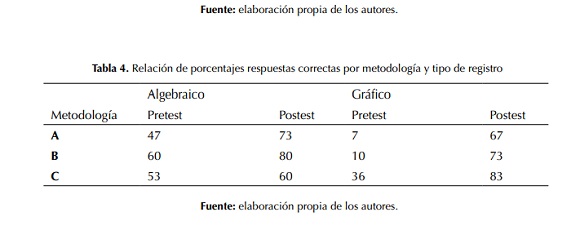
La tabla 4 resume la relación de porcentajes de respuestas correctas por metodología y tipo de registro, una simple inspección, basada en la distribución de las proporciones en cada celda, permite notar diferencias significativas entre las metodologías y los tipos de registro en los distintos momentos de la evaluación, dejando claro, de este modo, la influencia de las metodologías y tipos de registro en la comprensión del concepto por parte de los estudiantes.


Discusión
Los resultados obtenidos permiten evidenciar, en primer lugar, cuál es la preferencia en el momento de articular diferentes registros de representación semiótica en el proceso de aprendizaje del tema de funciones por parte de los estudiantes. Sobre este punto es necesario considerar tres aspectos fundamentales:
A nivel de comprensión conceptual: se comprobó que en el momento de definir funciones y diferenciarlas de las relaciones los estudiantes utilizan términos o elementos del lenguaje matemático tales como relación uno a uno, relación de correspondencia, única imagen, conjuntos de partida y de llegada, y que, de ellos, derivan el dominio y el rango. En el momento de proponer ejemplos de cada una de ellas existe cierta clasificación, es decir, para las relaciones utilizan diagramas de Venn o gráficas en el plano cartesiano y para las funciones utilizan gráficas en el plano cartesiano o expresiones algebraicas; en las gráficas en el plano cartesiano se observa la masiva utilización del criterio de la recta vertical paralela al eje de las ordenadas, pero mediante una apreciación de los puntos de corte como la cantidad de valores de Y que están asociados a un valor de X. Al proporcionarles funciones en diversos registros de representación, se observa buenos resultados para identificar sus características (dominio, rango, intervalos de crecimiento, asíntotas, entre otros), ofreciendo mejores resultados a partir del registro gráfico. Se observó, también, una disminución de los errores cometidos en el primer cuestionario y que se supone fueron aclarados y reforzados en la realización de los talleres alrededor de los conceptos de precálculo (temas de aritmética y algebra).
A nivel de habilidades: se evidenció en los tratamientos B y C que los estudiantes, a través de las diferentes actividades propuestas, incorporaron en el esquema de búsqueda de soluciones la articulación de los diversos registros de representación. Partiendo de la expresión algebraica proponen una tabla de valores y luego los representan en el plano cartesiano. En este punto del proceso, las dificultades se centraron en la manipulación incorrecta de los conjuntos numéricos, así como en la utilización incorrecta de la calculadora. Partiendo del registro gráfico, los estudiantes identifican parejas ordenadas de la misma, así como su dominio y rango. Cabe destacar que clasifican funciones a partir del registro gráfico, pero presentan dificultades en representaciones gráficas de funciones cuyo dominio son los números naturales o en funciones definidas a tramos o por partes, aumentando la dificultad al intentar hallar las expresiones algebraicas asociadas a ellas, tal como lo afirman en su investigación GARCÍA, VÁSQUEZ e HINOJOSA (2004), quienes encontraron que las mayores dificultades de aprendizaje yacen en las tareas de pasaje entre registros semióticos del concepto de función, particularmente en el pasaje del registro gráfico al algebraico.
A nivel de actitudes: a través de los talleres, el post-test y la entrevista, los estudiantes de los diversos grupos se sintieron más motivados en el desarrollo del tema. Argumentan que usualmente las clases de matemáticas son muy rutinarias y que siempre el docente habla o explica el tema y ellos copian e intentan seguirle el ritmo al profesor. En cambio, a través de la investigación, ellos tenían de cierta forma el control sobre su proceso de aprendizaje, ya que tenían el espacio para socializar sus concepciones en pequeños grupos y ya con ellas afinadas expresarse con mayor seguridad en la socialización a nivel grupal. Otro aspecto a destacar es que en la prueba diagnóstica el índice de no respuesta fue alto, pero en la prueba final dicho porcentaje disminuyó sustancialmente, aspecto que muestra en el estudiante mayor compromiso académico y mejores herramientas a la hora de buscar soluciones.
Al comparar los resultados de las dos pruebas aplicadas en esta investigación (pretest y postest), se observó mejoramiento en todos los grupos como posible efecto de las diversas metodologías, resultados avalados por la presencia de diferencias significativas en la distribución de las proporciones de respuestas correctas entre los grupos analizados. A nivel general, los grupos que ofrecieron mejores resultados fueron aquellos que estuvieron sujetos a metodologías diferentes de la tradicional, es decir, que la articulación de los diversos tipos de representación semiótica surge como una alternativa para el mejoramiento del rendimiento académico de los estudiantes.
Por otra parte, a pesar de que existieron mejoras académicas a nivel de los ejercicios, siguen presentándose errores en la búsqueda de las soluciones. Brousseau afirma, sobre la causa de los errores en los estudiantes, que un estudiante no falla por falta de conocimiento, sino al contrario: que los errores se deben a un conocimiento anterior (citado en BORBÓN, 2003). Aspecto que sugiere entrar a revisar las prácticas pedagógicas que utilizan los docentes en la educación básica y media en nuestro sistema educativo, ya que los estudiantes están ingresando al sistema de educación superior con una larga lista de concepciones imprecisas alrededor de los diferentes temas matemáticos.
En lo relativo a la solución de problemas, se evidenció en los estudiantes del grupo C (tratamiento que articulaba los diversos registros de representación) un nivel de desempeño destacado, seguido del rendimiento de los estudiantes del grupo B (favorecimiento del registro gráfico). En ellos se observó una actitud positiva ante situaciones no rutinarias, ya que dentro de las actividades que desarrollaron exhibieron un mejor dominio de conceptos matemáticos, así como una actitud más comprometida en la búsqueda de soluciones, lo que derivó en que los índices de no respuesta fueran bajos y en que los estudiantes proporcionaran justificaciones para cada acción adelantada durante las actividades.
Los resultados obtenidos están en línea con los postulados teóricos de esta investigación, de acuerdo con los cuales la enseñanza de los conceptos matemáticos, a diferencia de los conceptos inherentes de muchas disciplinas, no se pueden abordar directamente, por lo que se requieren formas que los representen. Como indican FONT, GODINO y DE AMORE: “El problema surge cuando nos interesamos por los tipos de objetos que se relacionan, los criterios de correspondencia y la finalidad con la que se establecen las relaciones” (2007 p. 3). En este sentido, DUVAL (1998) afirma que los objetos matemáticos no son directamente accesibles a la percepción humana o a la experiencia intuitiva inmediata. Sosteniendo, por un lado, que la aprehensión de los objetos matemáticos no puede ser otra cosa que aprehensión conceptual y, por otro, que solamente por medio de las representaciones semióticas es posible una actividad sobre los objetos matemáticos. Además, afirma que un concepto se va construyendo mediante tareas que impliquen el uso de diferentes sistemas de representación y promuevan la articulación coherente entre representaciones. HITT (2000) afirma que el conocimiento de un individuo sobre un concepto es estable si es capaz, sin contradicciones, de articular diferentes representaciones de este.
Con base en lo anteriormente expuesto, y apoyado en los resultados obtenidos en la investigación, se puede confrontar la validez de lo afirmado por HITT (2000) y DUVAL (1998) respecto a los beneficios que trae al estudiante en la apropiación de conceptos matemáticos el uso y articulación de las diversas representaciones semióticas.
En referencia a la forma como los estudiantes utilizan las distintas representaciones semióticas, se evidenció, en los tres grupos y tras la aplicación del pretest, que los estudiantes usaban con mayor intensidad el registro de representación algebraico, existiendo cierto abandono o escasa utilización del registro gráfico. Este hallazgo es importante si lo consideramos como una luz en el complejo mundo de la representación de conceptos, tal y como lo advierte RICO (2009). Si se les proporcionaban expresiones algebraicas de funciones, los estudiantes hacían una tabla de valores utilizando siempre valores enteros,posteriormente los ubicaban en el plano cartesiano, luego unían los puntos (proceso mecánico) para, a partir de la gráfica, aplicar diversos procesos de comprobación de las características de la misma, tales como el dominio y el rango, que ya habían determinado de forma algebraica. Adicionalmente, en aquellos ejercicios donde se proporcionó una representación gráfica, se observó que los estudiantes dieron respuestas incorrectas, incoherencias y, en el peor de los casos, no realizaron proceso alguno. Lo anterior pone de manifiesto, por un lado, el poco uso del registro gráfico en la enseñanza y, por otro, la poca legitimidad institucional que se da al trabajo con dicho registro durante la enseñanza (GONZÁ- LEZ-MARTÍN y CAMACHO, 2004).
En el postest se encontró mayor dominio en la articulación de los diversos registros de representación. Aspecto que se manifestó en los resultados de los ítems del 4 al 8 en la prueba (véase anexo A), ya que en ellos se proporcionaron planteamientos en lenguaje formal matemático, registro algebraico, registro gráfico y forma tabular, y los estudiantes debían buscar las respectivas soluciones a las actividades propuestas.
En el numeral 9 del postest (véase anexo B) se evidenció mejoría en el nivel académico de los estudiantes de los grupos B y C, ya que inicialmente debían interpretar una situación en contexto para proponer una representación gráfica que se ajustara a dicho comportamiento con su respectivo argumento. En esta parte de la prueba los estudiantes hicieron razonamientos, argumentaron sus decisiones y propusieron una gráfica que, en la mayoría de los casos, fue correcta (73% de los estudiantes del grupo B y el 83% de los del C resolvieron acertadamente el problema). Al observar las gráficas incorrectas, se evidencia, igualmente, la articulación de los diversos esquemas de representación, ya que los estudiantes identificaron las magnitudes, determinaron su relación y propusieron una gráfica, argumentando que era una función creciente como efecto del vínculo de proporcionalidad directa entre las variables, e incluso algunos llegaron a afirmar que era una función lineal con pendiente positiva.
Conclusiones Los estudiantes que ingresan a primer semestre de universidad llegan con un cúmulo de conceptos matemáticos que, en la mayoría de los casos, son imprecisos y les acarrean dificultades conceptuales en su aprendizaje. Esto puede deberse, en muchas circunstancias, a la aplicación en el aula de una metodología tradicional que privilegia el uso excesivo del registro de representación algebraico, y, en consecuencia, se encamina a utilizar el registro gráfico mediante la representación en el plano cartesiano, pasando por la representación tabular de valores, pero desfavorece el traspaso de entre los diferentes registros de representación semiótica, lo que dificulta la compresión del concepto.
Los docentes de matemáticas debemos propender en el aula no solo por la utilización de diversos registros de representación, sino también por la articulación coherente entre ellos. De esta forma, el estudiante podrá llegar a una mejor construcción y comprensión de los conceptos matemáticos.
En lo que respecta a la articulación de registros, se evidencian dificultades con mayor frecuencia cuando el estudiante realiza un traspaso del registro gráfico al algebraico, mostrando desconocimiento de algunos principios que son de utilidad para este fin como, por ejemplo: los principios de desplazamiento horizontal, desplazamiento vertical y principios de reflexión y simetría.
A nivel general, se evidencia en el grupo de estudiantes que formaron parte de la investigación que sus respuestas suelen estar dadas en el registro en que ha sido propuesto el ejercicio, o se recurre comúnmente al registro algebraico para justificarla, posiblemente debido a que es el registro que más han utilizado en su proceso de formación académica durante su educación básica y media.
Referencias
ARTIGUE, M. La enseñanza de los principios del cálculo: problemas epistemológicos, cognitivos y didácticos. In: ARTIGUE, M.; DOUADY, R.; MORENO, L. y GÓMEZ, P. (eds.), Ingeniería didáctica en educación matemática. Grupo Editorial Iberoamericano. Ciudad de México: México, 1995. pp. 97-140.
JAIMES, L. A.; CHAVES, R. F.; HERNÁNDEZ, C. A. Planteamiento de una ecuación diferencial lineal de primer orden que modela un problema de mezclas: Una dificultad en la movilización entre registros de representación, lengua natural y algebraico. Elementos, 5(5), 23-31. 2015.
BORBÓN, A. Concepciones de profesores sobre varios conceptos del cálculo diferencial. Centro de Investigación y de Estudios Avanzados del IPN. Ciudad de México: México, 2003.
GONZÁLEZ-MARTÍN, A. y CAMACHO, M. Legitimization of the Graphic Register in University Teaching. The Case of the Improper Integral. In: HOINES M. J. y FUGLESTAD A. B. (eds.) Proceedings of the 28th International Conference for the Psychology of Mathematics Education, 2 ed., Bergen: Noruega, 2004. pp. 479-486.
D’AMORE, B. Objetos, significados, representaciones semióticas y sentido. Revista latinoamericana de investigación en matemática educativa (RELIME), 9(1), 177-196. 2006.
DUVAL, R. Registres de représentation sémiotique et fonctionnement cognitif de la pensée. Annales de Didactique et de Sciences Cognitives, 5, 37-65. 1993.
DUVAL, R. Registros de representación semiótica y funcionamiento cognitivo del pensamiento. In: HITT, F. (ed.), Investigaciones en Matemática Educativa II. Grupo Editorial Iberoamericano. Ciudad de México: México, 1998. pp. 173-201.
FONT, V.; GODINO, J.; D’AMORE, B. Enfoque ontosemiótico de las representaciones en educación matemática. For the Learning of Mathematics, 27(2), 3-9. 2007.
GARCÍA, L.; VÁSQUEZ, R.; HINOJOSA, M. Dificultades en el concepto de función en estudiantes de ingeniería. Revista Latinoamericana de Investigación en Matemática Educativa, 7(24), 27-34. 2004.
GUTIÉRREZ, S. I. Caracterización de tratamientos y conversiones: el caso de la función afín en el marco de las aplicaciones. Universidad Pedagógica Nacional. Bogotá D.C: Colombia, 2007.
GUZMÁN, I. Registros en juego en el concepto de función, comportamiento de una muestra de estudiantes chilenos. XVII Semana de la Matemática de la Universidad Católica de Valparaíso. Universidad Católica de Valparaíso. Valparaíso. 1990.
GUZMAN, I. Registros de representación, el aprendizaje de nociones relativas a funciones: voces de estudiantes. Revista latinoamericana de investigación en matemática educativa (RELIME), 1(1), 5-21. 1998.
HITT, F. Funciones en contexto. Proyecto sobre visualización matemática. Departamento de Matemática Educativa Cinvestav. Ciudad de México: México, 2000.
IBARRA, S.; BRAVO, J.; GRIJALVA, A. El papel de los registros de representación semiótica en la enseñanza del cálculo diferencial. XII Semana de Investigación y Docencia en Matemáticas (pp. 107-114). Departamento de Matemáticas. Universidad de Sonora. Hermosillo, México. Recuperado de: http://semana.mat.uson.mx/ MemoriasXVII/XII/IbarraOlmos.pdf. 2002.
NÁPOLES, J.; GONZÁLEZ, T.; GENES, F.; BASABILBASO, F.; BRUNDO, J. El enfoque histórico problémico en la enseñanza de la matemática para ciencias técnicas: el caso de las ecuaciones diferenciales ordinarias. Acta Scientiae, 6, 41-59. 2004.
PLANCHART, O. La visualización y la modelación en la adquisición del concepto de función. Universidad Autónoma del Estado de Morelos. Cuernavaca, México. Recuperado de: http://ponce. inter. edu/cai/tesis/oplanchart/inicio. Pdf. 2002.
RICO, L. Sobre las nociones de representación y comprensión en la investigación en educación matemática. PNA, 4(1), 1-14. 2009.
VÁSQUEZ, S. El concepto de función a través de la historia. Revista Iberoamericana de Educación (Unión), 1(16), 141-155. 2008.
Anexo A. Prueba pretest
Instructivo: esta actividad tiene como fin identificar el nivel de dominio que poseen los estudiantes que inician el curso de Cálculo Diferencial acerca de conceptos básicos y necesarios para el desarrollo del curso. Por tal razón, se recomienda diligenciarlo con la mayor sinceridad posible.
INFORMACIÓN GENERAL

Municipio donde estudió su bachillerato: ________________________________
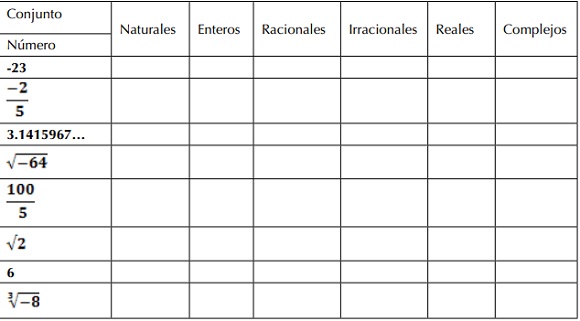
1. Marcar con una X al conjunto numérico al a que pertenece cada número proporcionado en la siguiente tabla.
Si ubicas los siguientes pares coordenados en el plano cartesiano, ¿en qué cuadrante se encuentran?
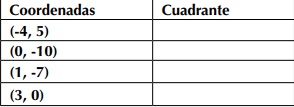
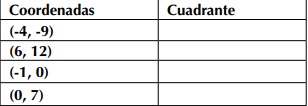
2. En matemáticas comúnmente se utilizan los términos ecuación e inecuación. Da un ejemplo de cada una de ellas y establecer sus diferencias.
3. Una función f de un conjunto X a un conjunto Y es una regla que asocia a cada elemento x de X un único elemento y de Y. El elemento y se llama la imagen de x bajo f y se denota por f(x). El conjunto X se llama dominio de la función. El rango de la función consta de todas las imágenes de los elementos de X.
La anterior definición es: Verdadera Falsa
Justificación
4. En la siguiente gráfica identifique el dominio y el rango de la función. ¿El #3 pertenece Y al rango?
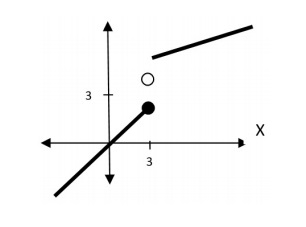
¿Existe una función en la que le corresponda 1 a cada número positivo; -1 a cada número negativo y 0 al 0?
Explique:
5. Evalúe la función f(x) = ax, cuando a = 2 y -1 ≤ x ≤ 4.
Dibuje la gráfica de la siguiente función ![]() . ¿Qué sucede en x = 4?
. ¿Qué sucede en x = 4?
Anexo B. Prueba postest
1. ¿Cuál es la definición de función?
2. ¿Qué diferencia hay entre una relación y una función? Dé dos ejemplos de cada una.
Ejemplos:
3. ¿Existe una función en la que le corresponda a cada número diferente de 0 su cuadrado y al 0 el -1? Explica tu respuesta.
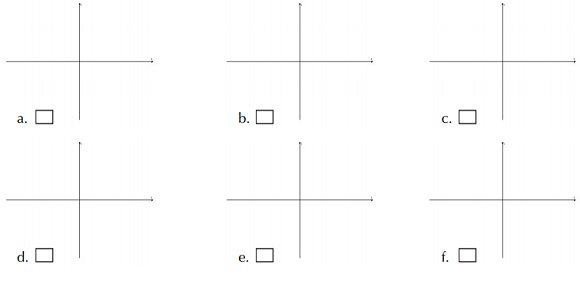
4. Indicar la gráfica que representa una función cuyo dominio es {x | 2 ≤ x ≤ 6}y cuyo rango es {y | -1 ≤ y ≤ 4}
5. Dada la función f, definida f: {números reales} → {números reales}, donde f(x)=4.
a. ¿Cuáles de los números ![]() , pertenecen al dominio de f(x)?
, pertenecen al dominio de f(x)?
b. Explica. ¿Cuáles de los números![]() pertenecen al conjunto imagen de f(x)?
pertenecen al conjunto imagen de f(x)?
Explica.
c. ¿Cuáles de los siguientes pares ordenados ![]() ( son elementos de la gráfica de f(x)?
( son elementos de la gráfica de f(x)?
6. Sea la gráfica de la función:
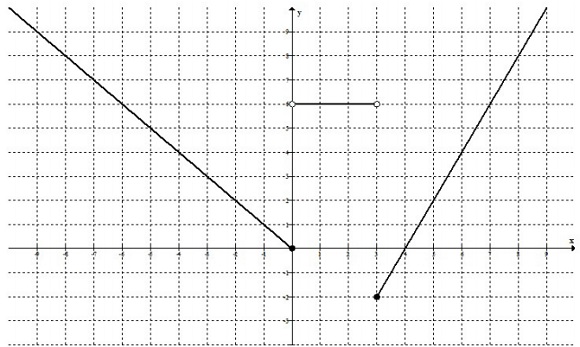
a. Construya una tabla de valores con algunos puntos que pertenezcan a la gráfica de la función dada:

b. Escriba la expresión algebraica que define la función asociada a la gráfica.
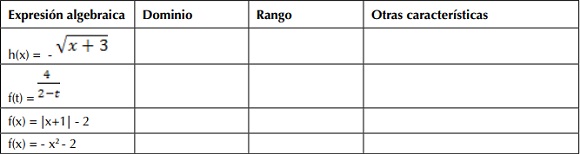
7. Para cada una de las siguientes expresiones completa la información solicitada:
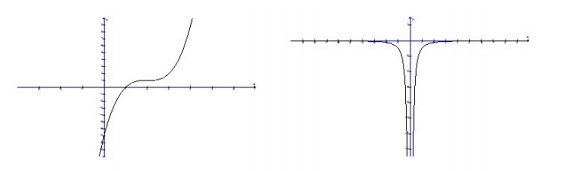
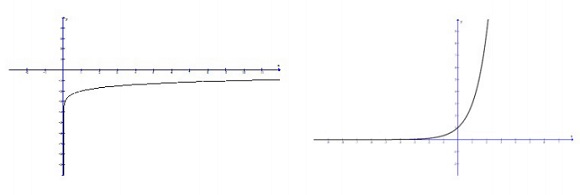
8. Clasifica las siguientes funciones según las características de su gráfica en: racional, exponencial, logarítmica o polinómica. Justifica tu respuesta
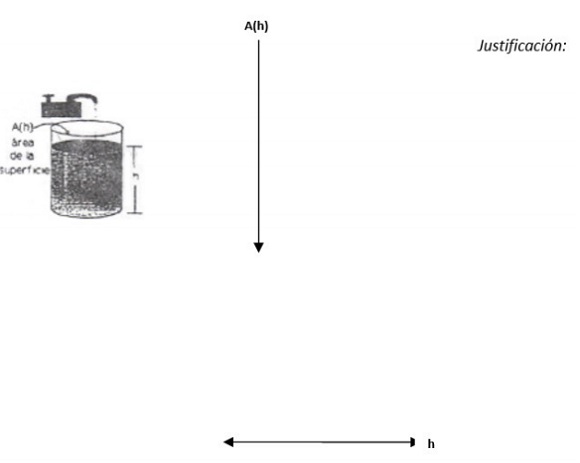
9. En las situaciones que se muestran a continuación, A(h) representa el área de la superficie de un líquido en un recipiente en función de su altura h.
Situación A: bosqueje la gráfica de la función A(h) que se genera a partir de las características del recipiente.
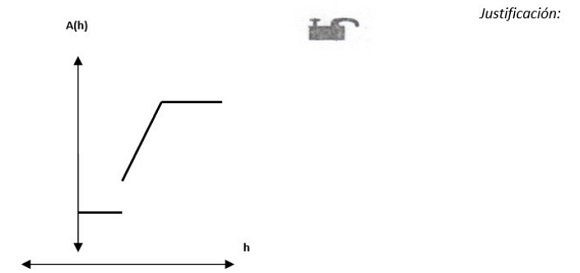
Situación B: bosquejar la forma del recipiente asociado a la gráfica dada.
License
Gondola, Ens Aprend Cienc. is an open-access publication, free of charge for authors and readers. The publication, consultation or download of the contents of the magazine does not generate any cost for the authors or the readers, since the Francisco José de Caldas District University assumes the expenses related to edition, management and publication. The peer evaluators do not receive any economic retribution for their valuable contribution. The work of all the actors mentioned above is understood as a contribution to the strengthening and growth of the research community in the field of Science Education.
As of December 1, 2018 the contents of the journal are published under the terms of the Creative Commons License Attribution-Noncommercial- ShareAlike 4.0 International (CC-BY-NC-SA 4.0), under which others may distribute, remix, retouch, and create from the work in a non-commercial way, give credit and license their new creations under the same conditions.
The copyright holders are the authors and the journal Gondola, Ens Aprend Cienc. The holders retain all rights without restrictions, respecting the terms of the license in terms of consultation, downloading and distribution of the material.
When the work or any of its elements is in the public domain according to the applicable law in force, this situation will not be affected by the license.
Likewise, we encourage authors to deposit their contributions in other institutional and thematic repositories, with the certainty that culture and knowledge is a good of all and for all.




















