Probabilidad y estadística para grado primero desde los organizadores curriculares

PROBABILIDAD Y ESTADÍSTICA PARA GRADO PRIMERO DESDE LOS ORGANIZADORES CURRICULARES

Probability and statistics for first degree from the curriculum organizers

Luisa Fernanda Rodríguez Molina¹

¹Estudiante de pregrado, Licenciatura en Educación Básica con énfasis en Matemáticas, Universidad Distrital Francisco José de Caldas. Bogotá, Colombia. Contacto: papillonminuit@hotmail.com

Recibido: 3 de junio de 2014 / Aceptado: 28 octubre de 2014

Para citar este artículo: Rodríguez, L. F. (2014). Probabilidad y estadística para grado primero desde los organizadores curriculares. Góndola, Enseñ Aprend Cienc, 9(2), 44-59. doi: 10.14483/jour.gdla.2014.2.a04

RESUMEN

Se pretende visualizar los organizadores curriculares en el aula de matemáticas, es decir, la planificación local que se debe realizar para la enseñanza de las mismas, tomándose en cuenta la planificación y gestión de la clase; además, este artículo se fundamenta en el proceso de enseñanza de la probabilidad y estadística en grado primero de la educación básica; es decir, se trabaja con niños que oscilan entre las edades de seis a siete años de edad. De igual forma se muestra cada organizador curricular con las características generales junto con las características específicas para la enseñanza de probabilidad y estadística en el grado mencionado anteriormente. A fin de realizar esta indagación se construyó en primera instancia cada organizador y posteriormente una secuencia de actividades junto con su respectivo análisis. Este fue el producto de las actividades aplicadas donde se fomenta la utilización de cada organizador curricular para garantizar así un proceso de enseñanza-aprendizaje de la probabilidad y estadística en grado primero de forma adecuada.

Palabras Claves: estadística, organizadores curriculares representaciones.

ABSTRACT

This paper aims to visualize the curriculum organizers from a specific perspective on the mathematics classroom, ie, local planning to be done to teach them, taking into account planning and classroom management; addition, this article is based on the teaching of probability and statistics in the first grade of basic education, ie working with children who are between the ages of 6 and 7 years. Each curriculum organizer also shows the general characteristics with the specific teaching of probability and statistics at the level above characteristics. To this inquiry, was built in a first step each organizer and then a sequence of activities with their analysis, this analysis was the result of activities applied where the use of each curriculum organizer is encouraged to guarantee a process of teaching learning of probability and statistics in first grade appropriately.

Keywords: curriculum organizer, representations, statistical.

Introducción

El presente estudio se realizó en el marco de la práctica intermedia de la Licenciatura en Educación Básica con énfasis en Matemáticas adscrita a la Universidad Distrital. El artículo se construyó a partir del estudio de los componentes que debe tener un currículo en nivel de planificación local para el área de matemáticas. Según Gómez (2002), en este tipo de planificación el profesor se centra en una estructura matemática específica, en este caso el estudio de la enseñanza de la probabilidad y la estadística en grado primero de la educación básica. Así, se toma como principal temática la estadística descriptiva y se resaltan los componentes principales que se evidencian en dicho curso, como por ejemplo, la importancia de utilizar representaciones gráficas y diferentes registros entre las mismas; es decir, la transformación entre registros, pasar de lo gráfico a lo simbólico o viceversa. Tales componentes se pueden identificar en la secuencia de actividades propuesta, en los resultados y análisis obtenidos de la misma, al ayudar a resaltar y argumentar el porqué es indispensable la existencia de organizadores curriculares que fortalezcan la enseñanza de las matemáticas y su aprendizaje.

Dicha secuencia se encuentra construida en términos de organización de la clase, propuesta por Brousseau (1999), donde se tienen en cuenta las situaciones en las que una clase puede ser establecida, estas son: situación de acción, formulación, validación y por último la institucionalización. Por otra parte, se toman en cuenta los planteamientos metodológicos y didácticos de Godino (1998), donde se enfatiza la manipulación y la experimentación de los recursos didácticos que se ponen al alcance del estudiante; así, desarrollará progresivamente el sentido de la curiosidad y de la observación, logrando que, al usar el razonamiento y los procedimientos adecuados, aprenda a deducir, formular hipótesis, prever los resultados, generalizar o simplemente entender cuándo ocurre a su alrededor un suceso aleatorio.

En el contenido del artículo se presenta: en primer lugar, los organizadores curriculares que argumentan la secuencia didáctica, con evidencias de las actividades aplicadas y con algunas conclusiones de las mismas; entre estos organizadores, se hallará la fenomenología, sistemas de representación, dificultades, obstáculos y errores, por último los materiales y recursos en la enseñanza de la probabilidad y estadística. En segundo lugar, se presentan las planeaciones tomadas en cuenta para el análisis de los organizadores curriculares y los resultados, análisis y conclusiones.

Análisis fenomenológico

Segn Puig (1997) el análisis fenomenológico consiste en describir cuáles son los fenómenos que pueden ser modelizados segn la estructura matemática. Como se mencionó con anterioridad, la estadística descriptiva es un organizador curricular que es primordial incluir debido a que con este el profesor puede analizar, describir, caracterizar y clasificar los fenómenos que se pueden vincular en problemas matemáticos. Por otra parte, teniendo en cuenta la perspectiva filosófica de dichos conceptos que asumió Freudenthal (en Puig, 1997), el fenómeno se refiere a lo que se aparece a través de la experiencia y el nomeno (objeto de pensamiento) es el objeto de pensamiento mediante la razón; por lo tanto, el nomeno organiza mediante el pensamiento razonando fenómenos por los cuales podemos experimentar el objeto de pensamiento y en su análisis observar qué relación tiene la estructura matemática con esos fenómenos. Para la fenomenología de la estadística descriptiva se toma en primera medida la palabra ¨estadística¨ en general para llegar así al concepto específico, entonces se remite a la definición que propone Batanero (2001):

La estadística estudia el comportamiento de los fenómenos llamados de colectivo. Está caracterizada por una información acerca de un colectivo o universo, lo que constituye su objeto material; un modo preciso de razonamiento, el método estadístico, lo que constituye su objeto formal y unas previsiones de cara al futuro, lo que implica un ambiente de incertidumbre, que constituyen su objeto o causa final. (p. 6)

La autora afirma que la estadística descriptiva tiene como fin presentar resmenes de un conjunto de datos y poner de manifiesto sus características mediante representaciones gráficas, en donde se utilizan los datos para fines comparativos y no se usan principios de probabilidad.

Por otra parte, esos datos que son tomados para realizar el análisis estadístico, provienen de una gran variedad de fenómenos ya sea de la vida social, política y económica. Estos fenómenos tienen que ver con información cuantitativa que hay en los datos para poder así resumir dicha información, caracterizarla, tipificarla y disponerla de forma que pueda ser comparada con otras informaciones provenientes de datos masivos (Batanero, 2001).

Fenomenología didáctica

En este tipo de fenomenología (Puig 1997) se resaltan los fenómenos que organizan los conceptos, los cuales se encuentran presentes en la estructura matemática escogida (estadística descriptiva), en donde se debe tener en cuenta el ordenar, agrupar y clasificar datos estadísticos para construir tablas de fenómenos estadísticos de una variable. Lo anterior se puede lograr cuando el estudiante conozca la terminología estadística empleada, diferencie fenómenos de una variable, recopile fenómenos estadísticos de una variable, ordene, agrupe los datos y construya tablas estadísticas.

De igual forma, para el proceso de enseñanza y aprendizaje es importante que el estudiante interprete gráficos, ya que como afirma Nortes (1991) el estudiante debe transformar al lenguaje comn lo observado en las diferentes gráficas para pasar así a otra gráfica y para que posteriormente pueda transformar la información en conceptos estadísticos más complejos, como podría ser la frecuencia relativa o interpretar gráficos que contengan información más compleja, como por ejemplo, el clima de una región o el movimiento de una población.

En el mismo orden de ideas, para que el estudiante pueda desarrollar un adecuado objeto mental debe tener en cuenta aspectos como la cardinalidad, la ¨información referente al tamaño (la numerosidad) de las colecciones de objetos¨ y la ordinalidad ¨indicar el lugar que ocupa o debe ocupar un objeto dentro de una colección ordenada de objetos¨ (Godino, 2002, p. 171).

Fenomenología genética

Este tipo de fenomenología se refiere a las experiencias (fenómeno) para el desarrollo cognitivo de los estudiantes, teniendo en cuenta que el objeto mental puede cambiar constantemente y sobre todo porque la brecha entre el objeto mental y el concepto puede ser difícil de cubrir.

Los objetos mentales, segn Puig (1997), sirven como medio de organización para las estructuras matemáticas; es decir, el objeto mental es el fenómeno por el cual el matemático organiza los medios con el fin de definirlos conceptualmente.

Los fenómenos para la genética son similares a los de la didáctica, pero con la gran diferencia de que en este tipo se identifican los problemas cognitivos de los estudiantes para que se puedan solucionar; además de tener en cuenta los diferentes contextos tomando elementos de la praxis de anteriores procesos y considerando desarrollos cognitivos nuevos, por la estructura conceptual, para que se pretenda cubrir la brecha entre el objeto mental y el concepto.

Sistemas de representación

En los sistemas de representación se toma en cuenta la propuesta de Castro y Castro (1997), quienes evidencian la importancia de los sentidos para la educación matemática, en cuanto los seres humanos en el proceso de aprendizaje ponen en juego los canales de información, el auditivo y el visual en el desarrollo de recibir y transmitir conocimiento matemático.

Por otra parte, se toma la definición de representación que proponen dichos autores, la cual considera que las representaciones son notaciones simbólicas o gráficas en donde se pueden expresar conceptos y procedimientos matemáticos, así como características y propiedades. Así, en las actividades aplicadas para grado primero —específicamente para la enseñanza de la estadística descriptiva—, se toman en cuenta las diferentes representaciones que pueden ayudar al aprendizaje de la estadística en dicho grado; aunque también se reconoce que existen diferentes representaciones gráficas para la organización, clasificación y lectura de datos estadísticos, como las siguientes: diagrama de barras, gráficos de sectores y pictogramas.

Ahora, tomando en cuenta los anteriores tipos de gráficas —en donde se logra representar la clasificación de una serie de datos, los cuales pueden ser cualitativos o cuantitativos—, es posible afirmar que las gráficas utilizadas, principalmente para la enseñanza de la estadística descriptiva en grado primero, se basan en los pictogramas que por medio de imágenes proporcionales pueden insertar al estudiante al reconocimiento de la cantidad de objetos en un conjunto; por otra parte, se ha introducido al estudiante a las representaciones de tipo diagrama de barras, específicamente los histogramas, en donde los estudiantes han tenido que pintar las barras dependiendo del conteo realizado en las tablas de frecuencias absolutas. A continuación se presentan algunos ejemplos de las representaciones gráficas utilizadas en grado primero.

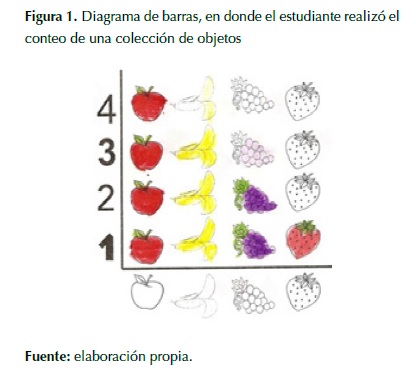
Con ayuda de las anteriores gráficas, se pueden alcanzar diferentes manejos e interpretaciones del concepto mencionado, ya que, segn Castro y Castro (1997), las transformaciones de cualquier información en diferentes representaciones gráficas se evidencian específicamente en el momento en el que los estudiantes pasan del conteo de figuras con características comunes a la determinación por medio de un símbolo numérico de su cantidad; de igual forma, en el momento en que los estudiantes recogen cierta información en una tabla de frecuencias, se reconoce el cardinal de cada conjunto o frecuencia absoluta del mismo. Finalmente se encuentra el momento en que los estudiantes pueden tomar la información de la tabla de frecuencias y representarla en una gráfica pictórica, concluyendo con la comparación tanto en la gráfica como en la tabla, las cantidades de cada conjunto a fin de realizar inferencias en lo que respecta al conjunto más grande, más pequeño o de igual cantidad de objetos.

Lo anterior es de gran ayuda para el desarrollo de la comprensión que los estudiantes pueden poseer en lo que respecta a tablas y gráficos estadísticos. Batanero (2001) afirma que en las representaciones gráficas y tablas el estudiante puede distinguir los valores originales de cada uno de los datos de forma individual, pasando posteriormente a la distribución de frecuencias; pero además de esto, puede construir la destreza en la lectura crítica de los datos, identificando a las vez cuatro niveles para la comprensión de gráficos estadísticos por parte de los estudiantes estos son (Batanero, 2001): leer los datos, leer dentro de los datos, leer más allá de los datos y leer detrás de los datos; los cuales serán de gran ayuda, para cuando el estudiante tenga la necesidad de interpretar algn gráfico estadístico presentado en su entorno, puede ser en la prensa, comercio, entre otros.

Dificultades, obstáculos y errores en la enseñanza de la probabilidad y estadística

Segn Gómez (1997, en Gómez, 2002) el proceso de enseñanza-aprendizaje de las matemáticas —que se remite al microsistema educativo o al nivel curricular correspondiente a la planificación para los profesores—, se presenta en cuatro dimensiones: cultural, formativa, cognitiva y social. De igual forma, el proceso identifica y organiza las dificultades segn características inherentes a la naturaleza de las matemáticas, de su enseñanza y su aprendizaje. Segn (Gómez, 2002) las dificultades ¨son los conocimientos que se ponen en juego cuando se produce un error¨(p. 14), y dichos conocimientos se relacionan con el objeto mental construido por los estudiantes al momento de relacionarse con el fenómeno.

Así pues, las diferentes dificultades se organizan de la siguiente manera: las asociadas a la complejidad de los objetos matemáticos: un aspecto principal de esta noción se refiere a los conflictos que presta el lenguaje comn para interpretar los signos matemáticos, pues este no precisa la exactitud de la disciplina matemática, además de las distintas interpretaciones que dicho lenguaje comn puede dar para un concepto matemático. De otro lado, las dificultades que se vinculan a los estados referentes a los sistemas que representan las relaciones entre distintos conceptos matemáticos, en su constante progreso de asimilación, siendo el primero, el estado donde se introducen un nuevo sistema de signos: suma, resta, multiplicación y división, por ejemplo; el estado estructural en donde el sistema antiguo organiza un nuevo sistema y el último estado es denominado autónomo, donde los signos actan con significados propios.

Detallando un poco más estas dificultades, se tienen las dificultades asociadas a los procesos de pensamiento matemático, las cuales se manifiestan en la naturaleza lógica de las matemáticas, que no permiten obtener métodos intuitivos, conjeturas, contraejemplos, deducciones, etc. Dicha dificultad se encuentra relacionada con el sentido de los objetos matemáticos.

De otro lado, se encuentran las dificultades que se vinculan a los procesos de enseñanza. Hacen referencia a las que se presentan en la institución escolar, el currículo de matemáticas y con los métodos de enseñanza-aprendizaje; entre ellos, la ausencia de materiales didácticos, el abuso de la metodología tradicional y baja formación de la planta docente con respecto a enfoques pedagógicos y conocimiento didáctico.

Finalmente, se presentan las dificultades asociadas al desarrollo cognitivo de los estudiantes. Se encuentra relacionada con el conocimiento didáctico del docente, pues este permite conocer e interpretar las acciones de los estudiantes a través de los estadios de desarrollo intelectual.

Obstáculos en el razonamiento estadístico

En lo que respecta a la identificación de los obstáculos en grado primero, en relación con el razonamiento estadístico, Socas (1997) afirma que el concepto de obstáculo se presenta bajo la denominación de obstáculo epistemológico. Bachelard (1938) considera que:

...hay que planearse el problema del conocimiento científico en términos de obstáculos. Y no se trata de considerar obstáculos externos, como la complejidad y la fugacidad de los fenómenos, ni tampoco de culpar la debilidad de los sentidos y de la mente humana, pues es precisamente, en el mismo acto de conocer, íntimamente, cuando surgen, como una necesidad funcional, torpezas de entendimiento y confusiones. Es ahí donde mostraremos causas de inercia que llamaremos obstáculos epistemológicos. (en Socas, 1997, p. 135)

Sobre la base de lo anterior se muestra a continuación la clasificación realizada por Socas (1997) de dichos obstáculos; a la vez se encontrarán los posibles errores que se hallan en la enseñanza de la probabilidad y la estadística:

Obstáculos ontogénicos: se refieren a las características del desarrollo del niño; por ejemplo: para comprender la idea de probabilidad se requiere un cierto razonamiento proporcional, por lo que un niño muy pequeño no puede comprender la probabilidad.

Obstáculos didácticos: se refieren al resultado de una opción o de un proyecto del sistema educativo, esto es, de las elecciones didácticas que se realizan para establecer la situación de enseñanza, en otras palabras, obstáculos que se dan como resultado de una inadecuada forma de enseñar un concepto; por ejemplo, al introducir la definición de frecuencia absoluta en una tabla de valores, los estudiantes de grado primero suelen confundirse debido a su escaso conocimiento del concepto como tal, o también se puede dar dicho obstáculo en el momento de introducir nuevos símbolos matemáticos o conceptos matemáticos, como por ejemplo, las fracciones.

Obstáculos epistemológicos: están intrínsecamente relacionados con el propio concepto. Se les puede encontrar en la historia de los mismos conceptos. Lo cual quiere decir que se deban reproducir en el medio escolar las condiciones históricas donde se les ha vencido; por ejemplo, las circularidades que se presentan en las diferentes definiciones del significado de la probabilidad (clásica, frecuencial y subjetiva) que mostraron en su día la necesidad de una definición axiomática.

Materiales y recursos en la enseñanza de la probabilidad y la estadística

En esta etapa se toma la identificación que realiza Coriat (1997), en lo que atañe a los materiales y los recursos que se utilizan diariamente en el aula de matemáticas. Se tienen en cuenta las definiciones brindadas por dicho autor a fin de reconocer y caracterizar los recursos y materiales utilizados en grado primero.

Coriat (1997) define a los recursos como cualquier material no diseñado específicamente para el aprendizaje de un concepto o procedimiento determinado, que el profesor decide incorporar en sus enseñanzas; por ejemplo, el marcador para tablero, el tablero o el cuaderno del estudiante, las calculadoras, videos, programas de ordenador, diapositivas y el periódico, entre otros.

Por otra parte, el autor define los materiales didácticos como los herramientas diseñadas con fines educativos, por ejemplo, las hojas de trabajo preparadas por el profesor, materiales manipulativos, tal es el caso de los ábacos, regletas, geoplanos, dados y fichas de colores, entre otros.

Cabe resaltar que los anteriores materiales y recursos moldean todas las relaciones que pueden existir entre los objetos matemáticos, es decir, con los materiales y recursos el docente puede desarrollar diferentes conceptos entrelazándolos entre sí y generando características del objeto a medida que los estudiantes interactan con los materiales; también, el uso de materiales y recursos genera que los estudiantes salgan de la clase habitual (logarítmica) a una clase de experimentación, comprendiendo las afirmaciones y preguntas que realiza el docente en el desarrollo de la actividad, a esto se suma que por medio de la experimentación el estudiante encuentra razonamiento y respuestas a las cuestiones del profesor con mayor facilidad.

Entre los materiales utilizados para la enseñanza de la probabilidad y estadística se sigue a Batanero, C (2001), quien propone la clasificación que se realiza en la Tabla 1.

Cabe resaltar que los materiales de dicha clasificación corresponden a aquellos que se desearía que se utilicen en el aula de matemáticas, como método exploratorio en el cual los estudiantes puedan descubrir y manejar con mayor claridad los conceptos planeados. Sin embargo, se presentan falencias y vacíos en el momento de implementarlos por parte de los docentes en la enseñanza de la probabilidad estadística.

En este punto Coriat (1997) expone las dificultades que posiblemente generan los recursos y materiales, las cuales se pueden presentar en los siguientes niveles: curricular e infraestructura; currículo planificado; y del currículo implementado. La primera se refiere fundamentalmente a la formación inicial y permanente del profesor, es decir, la institución debería identificar continuamente los conocimientos que posee un docente de matemáticas acerca de los diferentes materiales disponibles en el aula y reconocer entre los mismos la importancia de utilizarlos y de saber aprovechar los insumos que pueden dar al proceso de enseñanza y aprendizaje. Por otra parte, una consecuencia que ocasiona dicha dificultad es la poca dotación de material del colegio, es decir, muchas veces pareciera que en los colegios no hay materiales y herramientas que apoyen la enseñanza y aprendizaje de las matemáticas, lo cierto es que en ocasiones se desconocen por completo, dado su escaso uso y conocimiento de cómo pueden ayudar en el aula de matemáticas, porque no hay espacios adecuados o simplemente porque no hay recursos monetarios para sustentarlos.

De otro lado, se presentan los recursos y materiales didácticos utilizados para la enseñanza de algunos conceptos de la probabilidad y estadística en grado primero. Cabe resaltar que entre esos materiales se encuentran también los juegos didácticos, que fueron diseñados previamente por los docentes en formación para una sesión de clase, contribuyendo a la familiarización y caracterización de sucesos aleatorios y representativos por parte de los estudiantes.

Para la enseñanza de la estadística se llevaron a cabo temáticas en donde se utilizaban variables cualitativas, se manejaron encuestas y clasificación de objetos dependiendo de las características: forma, tamaño, color, entre otros. A la par se utilizaron guías construidas por los docentes en formación, en las que se reflejaban comparaciones entre los datos a través de presentaciones, como gráficas de barras o las tablas de frecuencias, y en donde también se podía hacer comparaciones entre sí para realizar posteriormente lectura de los datos o entre los datos.

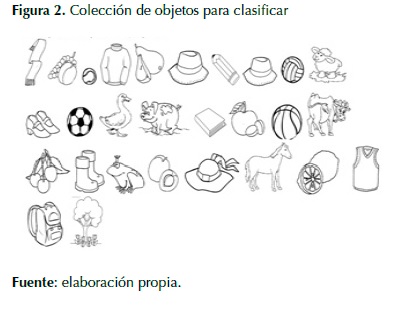
En la Figura 2 se evidencian las clasificaciones de objetos dependiendo de las características que tuvieran los objetos, por ejemplo, animales, frutas, tiles escolares, balones, zapatos y árboles.

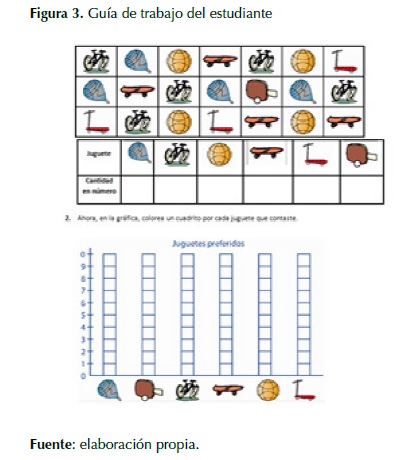
La Figura 3 es una de las guías que se presenta a los estudiantes, a fin de profundizar conocimientos adquiridos en la experimentación con los objetos. Se muestra una serie de objetos que deben ser clasificados por los estudiantes y, a la vez, se presenta una tabla de frecuencias en donde el estudiante debe identificar la cantidad de objetos que posee cada grupo establecido (frecuencia absoluta); por ejemplo, el grupo de las patinetas o el grupo de balones de basketball. Finalmente, el estudiante debe relacionar la cantidad establecida en la tabla de frecuencias que plasma en la gráfica de barras.

Por último, se muestra a continuación el juego - que fue fundamental para introducir a los estudiantes en sucesos aleatorios- ¨cruzando el río¨ propuesto por Gallardo, Cañadas, Martínez, Molina y Peñas (2007), la metodología general del juego es: se juega en parejas, cada jugador dispone de doce fichas (se utilizaron dos colores) y dos dados, posteriormente cada jugador debe colocar las fichas sobre las casillas (una por casilla), el primer jugador lanza los dados y suma los puntos obtenidos en las caras superiores de los mismos y pasa su ficha al otro lado del río, es decir, al lado del río del otro jugador. A continuación el segundo jugador lanza los dados y realiza el mismo procedimiento anterior, se contina el juego hasta que uno de los jugadores pase todas las fichas al otro lado del río.

Al reconocer intuitivamente por medio de comparaciones, las anteriores exploraciones ayudaron a los estudiantes a identificar la posibilidad de ocurrencia de un suceso. Puesto que los estudiantes en este grado de escolaridad no poseen conocimientos de fracciones podían comparar los cardinales de los conjuntos, identificando entre sí el conjunto que poseía mayor cantidad y menor cantidad de objetos.

Una secuencia de actividades para la enseñanza de la probabilidad y la estadística

Actividad diagnóstico

En esta actividad se ponían en juego los conocimientos anteriormente adquiridos a través de los fenómenos: clasificación de objetos de la cotidianidad; su representación; establecimiento de la cardinalidad de los conjuntos de los animales y juguetes; y la identificación de la gráfica correcta. Estos pertenecen a la fenomenología didáctica (Puig 1997) y organizan las siguientes estructuras matemáticas: clasificación de objetos por atributos, la cardinalidad de conjuntos, el conteo y las representaciones gráficas (tabla de frecuencias absolutas y de barras). Cabe resaltar que anteriormente se realizaron clasificaciones de objetos con atributos específicos, es decir, segn su forma.

Los estudiantes reconocían de antemano, gracias al docente, dicha característica que esta actividad no traía, es decir, se realizaron las correspondientes indicaciones de la actividad, pero no proporcionaron con anticipación las características que los estudiantes debían tener en cuenta para la clasificación los objetos; al contrario, se planteaba una actividad en donde ellos pudieran caracterizar los objetos segn su propia perspectiva de los objetos.

Por lo anterior, en la clasificación se dieron diversos resultados a partir de los objetos mentales, que segn Puig (1997) son los medios (cognitivos) de organización para las estructuras matemáticas, a través de la organización de los medios (físicos) —que para este caso fueron los recortes de las figuras con forma de animales, ropa, fruta etc. en la cartulina, que los estudiantes plantearon para la actividad— con el propósito de definirlos conceptualmente (establecimiento de las clases). Entre los resultados se obtuvieron:

Primer objeto mental, clasificación por colores de los objetos: en esta clasificación los estudiantes decidieron caracterizar los objetos por un color, es decir, no tomaron en cuenta los atributos de los objetos sino que decidieron crear una nueva característica o atributo por medio de los colores de los objetos que iban pintando.

Segundo objeto mental, clasificación por atributos de los objetos: en esta clasificación los estudiantes escogieron los objetos que correspondían a un conjunto específico, el cual podía ser definido o caracterizado por una palabra en general. Dichos conjuntos fueron en algunos casos: los tiles escolares, ropa (en donde se podía incluir desde los zapatos hasta los sombreros), las frutas, los tiles escolares, los animales y por último el conjunto que poseía un solo elemento, el cual podía ser identificado en los objetos pertenecientes a las plantas (árbol).

Por otro lado, en esta clasificación se presentaron a su vez clasificaciones an más específicas, es decir, clasificaron los animales, las plantas, las frutas, los tiles escolares y los balones normalmente; pero cuando se aproximaron a la clasificación anterior de la ropa, algunos estudiantes manifestaron que este conjunto se podía dividir en el conjunto de los zapatos (tercer objeto mental), en el conjunto de los sombreros y en el conjunto de los abrigos o de ropa para abrigar.

Los diferentes resultados también se deben a los diferentes modelos que pueden surgir en una situación y que son utilizados por los estudiantes para representar mltiples relaciones y estructuras matemáticas; es decir, matematizar una situación (Castro y Castro, 1997). Se pudieron evidenciar los pasos dados por Lange y Swetz (en Castro y Castro, 1997) para el proceso de una modelización, donde el primero consiste en identificar el problema, buscando regularidades en la información, a fin de organizarla. A su vez se evidenció en el momento en que los estudiantes empezaron a recortar las diferentes figuras y organizarlas por grupos, teniendo en cuenta alguna propiedad (tamaño, forma, color, etc.) antes de pegarlas en la cartulina y en la fase de comunicación.

En el segundo paso, el problema se interpreta a través de símbolos matemáticos, que se ven reflejados en los diagramas de Venn o en la representación a manera de diagrama de barras, ya que la clasificación se presentó en filas. El tercer paso, la utilización de referentes teóricos, no se presenta. El cuarto y el que justifica la posible respuesta al problema, se presentó cuando se dieron diferentes propiedades que clasificaban los conjuntos mencionados anteriormente.

La siguiente guía de esta actividad consistía en el conteo de diferentes juguetes, reflejando dicho conteo en una tabla de frecuencias absolutas y en la representación de los resultados obtenidos en una gráfica de barras, en la que las representaciones expresan conceptos y procedimientos matemáticos (Castro y Castro, 1997). Las gráficas de barras permiten describir un conjunto de datos (Nortes 1991) y, a su vez, actan como modelos heurísticos en cuanto no las realizaron los estudiantes, ya que se hallaban ejemplificadas y ayudaron a la sustitución del concepto original, para que, de esta manera, se construya la noción de la representación del gráfico de barras.

De lo anterior se puede decir que los estudiantes hicieron uso del nmero tal y como plantea Castro, Rico y Castro (1991), es decir, el niño utiliza una secuencia verbal, realizando el conteo de cada uno de los juguetes obtenidos y a la vez reconociendo intuitivamente el cardinal del conjunto, es decir, la cantidad de objetos que un conjunto finito puede poseer, utilizando éste último el nmero como cardinal.

Por otra parte, en la gráfica de barras de los resultados, los estudiantes asignaron una correspondencia de cada juguete a un cuadrito perteneciente en la gráfica; es decir, por cada juguete que contaban pintaban un cuadrito en la gráfica en su correspondiente columna.

La actividad cumplió con el objetivo de la planeación, que consistía en el establecimiento de clases sobre la base de criterios que los estudiantes determinaron. De igual forma, se observaron nociones de la representación de gráficas de barras a través de la relación clase-cantidad, dicho fenómeno actuó a través de un modelo heurístico.

Aunado a lo anterior, se complementan las estructuras conceptuales trabajadas en anteriores clases, lo que conduce a la consolidación de nociones de la estadística, es decir, en la identificación de los datos en una gráfica de barras.

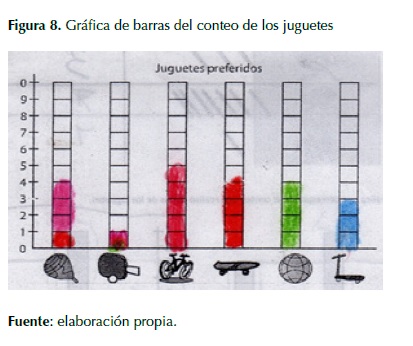
Por otra parte, se da al estudiante la definición de conjunto y con ello de clase, de manera no formal, en donde se establece la clasificación de objetos dependiendo de sus propiedades comunes y se enfatiza a la vez en las características comunes que cierta cantidad de objetos puede poseer; por otra parte, se toma también la construcción de nociones acerca del gráfico de barras, para después establecer la clasificación de clases pero con datos estadísticos, primero con datos cualitativos y después cuantitativos, para representarlos, si es posible en diferentes representaciones gráficas (diagrama de barras, tabla de frecuencia, pictograma, etc.).

Por último, el análisis de esta actividad tomó referentes de los componentes de una malla curricular, que ayudó a aclarar los mismos y verlos reflejados en la realidad. Al respecto, las diferentes representaciones pueden ser internas o externas (Castro y Castro 1997), las cuales se evidenciaron en la misma definición de fenómeno, puesto que se ponen en juego los medios cognitivos y los medios físicos que se representan mediante su correspondiente representación.

Actividad 1

En primera instancia se toma la guía diagnóstico, en donde los estudiantes utilizaron el conteo para la determinación del cardinal de un conjunto de objetos determinado. Por ejemplo, en este caso se utilizó en general el conjunto de las frutas, pero los estudiantes debían identificar el cardinal de cada conjunto específico, es decir, el de las manzanas, bananos, uvas y fresas, aplicando al mismo tiempo los usos del nmero que propone Castro, Rico y Castro (1996). En este contexto el símbolo corresponde a la caracterización de la cantidad de objetos en un conjunto, denominándolo nmero como código, que se puede manifestar a partir del uso del nmero como conteo; allí el estudiante identifica por medio del conteo la correspondencia de cantidad respecto a algn objeto y posteriormente lo representa con un símbolo.

A esto se suma que en el transcurso de la construcción de la gráfica se realizan preguntas a los estudiantes como: ¿en dónde hay más objetos? Por medio del conteo y de la comparación de cantidades aquéllos pueden diferir cuál conjunto posee más objetos, en otras palabras los estudiantes segn Godino (2002) en su obra Didáctica de las matemáticas para maestros, se encuentran en los niveles de comprensión de gráficos de: lectura literal, el cual consiste principalmente en leer los datos, es decir, los estudiantes pueden, a partir de la gráfica, deducir en dónde hay más o en dónde hay menos objetos; y el nivel de interpretar los datos, el cual apunta a leer dentro de los datos, y allí es necesario comparar cantidades y el uso de otros conceptos, como en este caso el conteo y la cardinalidad de conjuntos para deducir si hay más manzanas o uvas.

En esta actividad, se ha querido profundizar en las representaciones gráficas de las situaciones estadísticas, relacionadas con la clasificación de datos y frecuencias absolutas, sabiendo de ante mano que son conocimientos transmitidos indirectamente, debido a su complejidad conceptual; es decir, el estudiante no sabe que se encuentra identificando por medio del conteo de las representaciones de diferentes figuras y cantidades el concepto relacionado con frecuencias absolutas, sino más bien el estudiante, por medio de todos los procesos mencionados, está manipulando y adquiriendo el conocimiento para poder (más adelante en su educación matemática) reconocer los conceptos con mayor facilidad.

Es por esto que se ha decidido profundizar en las planeaciones en el desarrollo del conocimiento matemático con ayuda de las representaciones, ya que como menciona Castro y Castro (1997), los sentidos son de gran importancia para los seres humanos en el proceso de aprendizaje, pues ponen en juego los canales de información: el auditivo y el visual en el desarrollo de recibir y transmitir conocimiento matemático.

Actividad 2

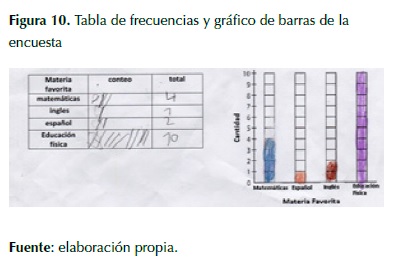
Para los objetivos de esta actividad se tenían en cuenta aspectos de estadística descriptiva, puesto que resumirían un conjunto de datos a través de diferentes representaciones gráficas (Godino 2002), trabajando la construcción de las nociones de población, su tamaño y muestra de la misma, a partir de datos cualitativos. De igual manera, se volvían a retomar las representaciones de la tabla de frecuencia y el gráfico de barras, pero con la diferencia de que estas se hacían a partir de una encuesta, contextualizando un poco más el objeto de aprendizaje, ya que se describían ¨fenómenos llamados de colectivo¨ (Batanero 2001, p.132), definición que propone este autor a la estadística.

Los fenómenos presentados hacen parte de la fenomenología didáctica (Puig, 1997) porque organizan los conceptos, es decir, a partir de la encuesta se observó el tipo de datos que fueron de carácter cualitativo y se determinó la población (tres encuestados), ya que los datos recolectados se hicieron en grupos de cuatro estudiantes. Con respecto al desarrollo de esta actividad, la representación abstracta que realizaron los estudiantes de la encuesta, es decir, el modelo utilizado (Castro y Castro 1997) concebido por la estructura mental, no era pertinente por lo que se presentaron unas dificultades referentes a la respuesta mltiple, es decir, los estudiantes an no comprendían que se debía escoger una nica respuesta sino que por el contrario establecían diferentes respuestas para una misma encuesta, por otra parte, se presentaron dificultades con respecto al nivel de lectura de algunos de los estudiantes y esto impidió que realizara la encuesta en su totalidad afectando posteriormente las gráficas, o también, de registrar doble repuesta a una misma pregunta, precisamente por el hecho de que no comprendía cada uno de los ítems de la encuesta; podría entenderse esta dificultad desde la planeación realizada, ya que no se tomó en cuenta todos los factores que podrían impedir la aplicación satisfactoria de la actividad.

Con respecto a las representaciones que cada estudiante realizó de sus encuestas, recopilando la frecuencia absoluta de cada opción de respuesta, se pudo observar que el tamaño de la población no era el correcto, por lo que el objeto mental (Puig 1997) en los estudiantes no era claro, esto se debió a dos factores: el primero, a que en el registro de la frecuencia absoluta no se tenía en cuenta que el encuestador también era encuestado y que era parte del tamaño de la población; el segundo, a que en dos grupos habían cinco estudiantes, por lo que no todos los integrantes del grupo tenían los mismos encuestados y al momento de registrar la tabla de frecuencia se presentaban dificultades, pues fue un conocimiento adquirido (Gómez 2007) donde se volvían a hacer las preguntas con los integrantes que no habían encuestado, llegando a registrar dos respuestas en una misma pregunta.

Conclusiones

Cuando inició la práctica intermedia los estudiantes se hallaban en un proceso de aprendizaje diferente, es decir, se encontraban en un proceso de aprender los nmeros, a sumar y a restar, pero al llegar los docentes en formación dicho proceso se pudo unificar con nuevas temáticas, que ayudaron a los estudiantes en su proceso de aprendizaje. En estas no solo se ponían en juego los conocimientos previos (los que se estaban llevando a cabo) sino que también ayudaron a que los estudiantes profundizaran e interactuaran con nuevos conceptos, como la probabilidad y la estadística.

Es posible que incluso el docente en formación haya tenido grandes sorpresas en este proceso, pues enseñar probabilidad y estadística en primaria, específicamente en grado primero no es fácil. Al contrario, gracias a la profunda indagación respecto al tema a enseñar y las diferentes estrategias que se pueden realizar en el aula para enseñar la probabilidad y la estadística, ayudaron a que el docente en formación empleara nuevos recursos en el aula, por ejemplo, los juegos (cruzando el río) y los materiales didácticos, para así, transmitir el conocimiento de forma adecuada, es decir, sin errores conceptuales por parte del mismo.

Teniendo en cuenta lo anterior, los conocimientos que los estudiantes poseían al iniciar la práctica docente con respecto a la probabilidad y la estadística eran pocos, lo cual se evidenció en la actividad diagnóstico, esto ayudó a que docente en formación pudiera conectar sus conocimientos matemáticos con la probabilidad y la estadística.

Por una parte se inició un proceso en donde el estudiante debía caracterizar un conjunto de objetos dependiendo de una característica comn, lo cual fue de gran facilidad para los estudiantes debido a que los objetos presentados eran muy familiares para ellos, es decir, eran tomados de la cotidianidad de los mismos ayudando a descubrir las características que podían componer un conjunto de objetos; por otra parte, se enfatizó en los estudiantes la caracterización de acuerdo a las formas, ya que se les dificultaba el reconocimiento de figuras que tuvieran forma geométrica (cuadrado, triángulo, rectángulo y círculo), para lo cual los estudiantes clasificaron objetos que tuvieran diferente forma y asimismo que las definieran por ellos mismos, permitiendo esto, que los estudiantes diferenciaran las clases y el cardinal, es decir, la cantidad de objetos que se encontraban en un conjunto (frecuencia absoluta), reconociendo en las gráficas de barras el resumen de la información brindada en un principio y también, identificaban conclusiones con respecto a los datos, como por ejemplo, qué conjunto posee más objetos y qué conjunto tiene menos objetos, entre otros.

Lo anterior se pudo llevar a cabo gracias al orden y especificidad de los contenidos y estructuras llevadas a cabo. Hubiese sido imposible encontrar alternativas de enseñanza del objeto matemático si no se indagara e informara adecuadamente para ello, por eso es de gran importancia un currículo que contenga todos los componentes para la enseñanza y aprendizaje de cualquier concepto matemático, no teniendo en cuenta un aspecto matemático que le sirve al profesor para afianzar sus conocimientos, sino también sus diferentes alternativas, caminos y representaciones que puede realizar con el objeto para alcanzar mayor entendimiento por parte de los estudiantes.

Por último, las actividades fortalecieron las dificultades que los estudiantes poseían con respecto a las nociones de direccionalidad, ya que con ayuda de las actividades y juegos psicomotrices los estudiantes no tomaban solo su cuerpo como de referencia, sino que también podían identificar en otros la dirección y orientaciones básicas.

Referencias bibliográficas

Batanero, C. (2001). Didáctica de la estadística. Granada: Universidad de Granada.

Brousseau, G. (1993). Fundamentos y métodos de la didáctica de las matemáticas. México: Grupo editorial Iberoamérica.

Castro, E. y Castro, E. (1997). Representaciones y Modelización. En L. Rico, E. Castro, E. Castro, M. Coriat, A. Marin, L. Puig, M. Socas. (Eds.). La educación matemática en la enseñanza secundaria (pp. 95-114) Barcelona: Horsori.

Coriat, M. (1997). Materiales, recursos y actividades: un panorama. En L. Rico, E.

Castro, E. Castro, M. Coriat, A. Marin, L. Puig, M. Socas. La educación matemática en la enseñanza secundaria (pp. 155-177). Barcelona: Horsori.

Gallardo, S., Cañadas, M. C., Martínez, M., Molina, M. y Peñas, M. (2007). Jugando con la Probabilidad. Recuperado de http://funes.uniandes.edu.co/1604/1/JugandoProbabilidad.pdf

Godino, J. (1998). Uso de Material Tangible y Gráfico- Textual En El Estudio De Las Matemáticas: Superando Algunas Posiciones Ingenua. En A. M. Machado y cols. (Ed.). Actas do Prof Mat (pp. 117-124). Associaçao de Professores de Matemática: Guimaraes, Portugal.

Godino, J. (2004). Matemáticas para maestros. Departamento de Didáctica de las matemáticas. Universidad de Granada. Recuperado de http://www.ugr.es/local/jgodino/

Gómez, J. (2007). Un nuevo paradigma en la enseñanza de la estadística. En G. I. Crisálida (Ed.). Educación estocástica. Didáctica de la probabilidad y la estadística (pp. 116-123). Bogotá D.C: Universidad Distrital Francisco José de Caldas.

Gómez, P. (2002). Análisis didáctico y diseño curricular en matemáticas. Ema, v.7, 251- 292.

Nortes, A. (1991). Encuestas y precios. España: Síntesis.

Puig, L. (1997). Análisis Fenomenológico. En L. Rico, E. Castro, E. Castro, M. Coriat, A. Marin, L. Puig, M. Socas. (Eds.). La educación matemática en la educación secundaria (pp. 61-94). España: Horsori.

Socas, M. (1997). Dificultades, obstáculos y errores en el aprendizaje de las matemáticas en la educación secundaria. En L. Rico, E. Castro, E. Castro, M. Coriat, A. Marin, L. Puig, M. Socas. (Eds.). La educación matemática en la enseñanza secundaria (pp. 125-154). Barcelona: Horsori.