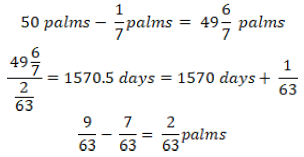DOI:
https://doi.org/10.14483/23464712.16041Published:
2020-05-01What students can learn from Fibonacci´s error in solving “The lion in the pit” problem
Lo que pueden aprender los estudiantes a partir del error de Fibonacci al resolver el problema “El león en el pozo”
O que os alunos podem aprender com o erro de Fibonacci ao resolver o problema “O leão no poco”
Keywords:
Fibonacci’s error, using history of mathematics in classroom, learning from errors, problem-solving (en).Keywords:
el error de Fibonacci, uso de la historia de las matemáticas en las aulas, aprendizaje a partir de errores, resolución de problemas (es).Keywords:
o erro de Fibonacci, uso da história da matemática em sala de aula, aprendendo com os erros, solução de problemas (pt).Downloads
References
AREM, C. A. Conquering math anxiety. A self-help workbook. Third edition. Brooks/Cole. Belmont, CA. 2010.
BAUER, J.; HARTEIS, C. (eds.). Human Fallibility: The Ambiguity of Errors for Work and Learning. Springer. Dordrecht. 2012. https://doi.org/10.1007/978-90-481-3941-5
BOALER, J. Limitless Mind. Learn, lead, and live without barriers. Harper One. New York. 2019.
BOOTH, J. L. et al. Evidence for cognitive science principles that impact learning in mathematics. In GEARY, D.C. et al. (editors), Acquisition of complex arithmetic skills and higher-order mathematics concepts. Academic Press. Amsterdam. 2017. pp. 297-325. https://doi.org/10.1016/B978-0-12-805086-6.00013-8
CALANDRI, F. De Arithmetica. Lorenzo da Morgiani y Giovanni Thedesco da Maganza. Florencia, 1491.
CHANG, H. Analysis on Using the History of Mathematics in Chinese Mathematics Textbooks. Journal for History of Mathematics, Seoul, Korea, v. 28, n. 1, pp. 15-29. 2015. https://doi.org/10.14477/jhm.2015.28.1.015
CLARK, K. M. et al. (editors). Mathematics, Education and History. Towards a harmonious partnership. ICME-13 monographs. Springer. Cham. 2018
DEAK, J. Your fantastic elastic brain. Stretch it, shape it. Little Pickle Press. Belvedere, CA. 2010.
DEKKER, S. The Field Guide to Understanding "Human Error". Third Edition. Ashgate Publishing Company. Farnham, UK. 2014.
DELL'ABBACO, P. Tratatto d'Aritmetica. Secondo la lezione del Magliabechiano XI, 86 de la Biblioteca Nazionale di Firenze. A cura e con introduzione di Gino Arrighi. Domus Galileana. Pisa. 1964.
DESCHAUER, S. Das zweite Rechenbuch von Adam Ries: eine moderne Textfassung mit Kommentar und metrologischem Anhang und einer Einführung in Leben und Werk des Rechenmeisters. Springer-Verlag. Berlin. 2013.
FAUVEL, J. Using History in Mathematics Education. For the Learning of Mathematics, Edmonton, Canada, v. 11, n. 2, pp. 3-6. 1991.
FAUVEL, J.; VAN MAANEN, J. (editors). History in Mathematics Education. The ICMI Study. Kluwer Academic Publishers. New York. 2002. https://doi.org/10.1007/0-306-47220-1
GIL, P., MARTINHO, M. H. The role of history of mathematics in fostering argumentation: Two towers, two birds and a fountain. In CERME 9 - Ninth Congress of the European Society for Research in Mathematics Education, Charles University in Prague, Faculty of Education; ERME, Feb 2015, Prague, Czech Republic. 2016. pp. 1817-1824.
HØYRUP, J. Jacopo da Firenze's Tractatus Algorismi and Early Italian Abbacus Culture. Birkhäuser. Basel. 2007. https://doi.org/10.1007/978-3-7643-8391-6
JANKVIST, U. T. A categorization of the "whys" and "hows" of using history in mathematics education. Educational Studies in Mathematics, Heidelberg, Germany, v. 71, n. 3, pp. 235-261. 2009. https://doi.org/10.1007/s10649-008-9174-9
JU, M. K.; MOON, J. E.; SONG, R. J. History of mathematics in Korean mathematics textbooks: Implication for using ethnomathematics in culturally diverse school. International Journal of Science and Mathematics Education, Heidelberg, Germany , v. 14, n. 7, pp. 1321-1338. 2016. https://doi.org/10.1007/s10763-015-9647-0
JUÁREZ RAMÍREZ, M. A.; HERNÁNDEZ REBOLLAR, L. A.; SLISKO, J. (). Fibonacci's motion problem "Two travellers": The solutions given by junior high-school students who were trained for Mathematical Olympiad. Latin American Journal of Physics Education, Mexico City, v. 8, n. 3, pp. 390-396. 2014.
KATZ, V. (editor). Using History to Teach Mathematics. An International Perspective. The Mathematical Association of America. Washington, D.C. 2000.
KATZ, V. J. A History of Mathematics. An Introduction. Third Edition. Addison-Wesley. Boston. 2009.
KATZ, V. J. Using history in teaching mathematics. For the Learning of Mathematics, C Edmonton, Canada, v. 3, pp. 13-19. 1986.
KLETZ, T. An engineer's view of human error. Third edition. Institution of Chemical Engineers. Rugby, UK. 2001.
LIGHTER, J. Mathematicians are human too. Mathematics Teacher, Washington, D.C., v. 93, n. 8, pp. 696-699. 2000.
LIU, P. H. Do teachers need to incorporate the history of mathematics in their teaching? Mathematics Teacher, Washington, D.C., v. 96, n. 6, pp. 416-421. 2003.
MARSHALL, G. L.; RICH, B. S. The role of history in a mathematics class. The Mathematics Teacher, Washington, D.C., v. 93, n. 8, pp. 704-706. 2000.
MATTEUCCI, M. C.; SONCINI, A.; CIANI, A. From failure to success: The potential beneficial role of error. In: COLUMBUS, A. M. (editor), Advances in Psychology Research. NOVA Science Publishers. New York. 2019. pp. 111-141.
METCALFE, J. Learning from Errors. Annual Review of Psychology, Princeton, n. 68, pp. 465-489. 2017. https://doi.org/10.1146/annurev-psych-010416-044022
MOYON, M. Teaching Mathematics and Algorithmics with Recreational Problems: The Liber Abaci of Fibonacci. In: BARBIN, É. et al. (editors). Proceedings of the Eighth European Summer University on History and Epistemology in mathematics Education (ESU-8) (Skriftserie 2019, nr. 11). Oslo Metropolitan University. Oslo. 2019.
PARK, J.; JANG, D. Study on Criticism and Alternative on the History of Mathematics Described in the Secondary School Mathematics Textbooks. Communications of Mathematical Education, Seoul, Korea, v. 29, n. 2, pp. 157-196. 2015. https://doi.org/10.7468/jksmee.2015.29.2.157
PETKOVIĆ, M. S. Famous Puzzles of Great Mathematicians. American Mathematical Society. Providence. 2009. https://doi.org/10.1090/mbk/063
RADFORD, L.; FURINGHETTI, F.; HAUSBERGER, T. (editors). Proceedings of the 2016 ICME Satellite Meeting of the International Study Group on the Relations Between the History and Pedagogy of Mathematics. IREM de Montpellier. Montpellier. 2016.
REASON, J. Human Error. Cambridge University Press. Cambridge, UK. 1990.
RIES, A. Rechnung auff der linihen. Maler. Erfurt. 1525.
SANFORD, V. The problem of the lion in the well. The Mathematics Teacher, Washington, D.C., v. 44, n. 3, pp. 196-197. 1951.
SANFORD, V. A Short History of Mathematics. The Riverside Press. Cambridge, MA. 1958.
SANFORD, V. The History and Significance of Certain Standard Problems in Algebra. AMS Press. New Work. 1972. This is a reprint edition of original edition published in 1927 by College Press, New York.
SCHORCHT, S. History of Mathematics in German Mathematics Textbooks. In: Clark, K. M. et al. (editors). Mathematics, Education and History. Springer. Cham. 2018. pp. 143-162. https://doi.org/10.1007/978-3-319-73924-3_8
SIGLER, L. E. Fibonacci's Liber abaci: a translation into modern English of Leonardo Pisano's Book of calculation. Springer. New York. 2002.
SINGMASTER, D. Sources in Recreational Mathematics. An Annotated Bibliography. Eight Preliminary Edition. The Puzzle Museum. London. 2004,
SLISKO, J. Self-Regulated Learning in A General University Course: Design of Learning Tasks, Their Implementation and Measured Cognitive Effects. Journal of European Education, Kayseri, Turkey, v. 7, n. 2, pp. 12-24. 2017.
STEUER, G.; DRESEL, M. A constructive error climate as an element of effective learning environments. Psychological Test and Assessment Modeling, Lengerich, Germany, v. 57, n. 2, pp. 262-275. 2015.
STRAUCH, B. Investigating Human Error: Incidents, Accidents, and Complex Systems. Second Edition. CRC Press. Boca Raton, FL. 2017. https://doi.org/10.4324/9781315251851
SULLIVAN, M. M.; PANASUK, R. M. Fibonacci numbers and an area puzzle: Connecting geometry and algebra in the mathematics classroom. School Science and Mathematics, Stillwater, Oklahoma, v. 97, n. 3, pp. 132-138. 1997. https://doi.org/10.1111/j.1949-8594.1997.tb17356.x
SWETZ, F. J. Seeking relevance? Try the history of mathematics. The Mathematics Teacher, Washington, D. C., v. 77, n. 1, pp. 54-47. 1984.
SWETZ, F. J. Using Problems from the History of Mathematics in Classroom. The Mathematics Teacher, Washington, D. C., v. 82, n. 5, pp. 370-377. 1989.
SWETZ, F. J. Mathematical expeditions: Exploring word problems across the ages. Johns Hopkins University Press. Baltimore. 2012.
TASKIN, D.; YILDIZ, C.; KANBOLAT, O.; BAKI, A. Reflections of Problem Solving Environment Based on Group Work: Example of Fibonacci Problem. Mediterranean Journal of Educational Research, Canakkale, Turkey, v. 14a, pp. 170-175. 2013.
TAYLOR, J. R. Human Error in Process Plant Design and Operation: A Practitioner's Guide. CRC Press. Boca Raton, FL. 2016. https://doi.org/10.1201/b19075
WELLS, D. Games and mathematics. Subtle connections. Cambridge University Press. New York. 2012 https://doi.org/10.1017/CBO9781139175838
WOODS, D. D. Behind Human Error. Second Edition. Ashgate Publishing Company. UK. 2010.
How to Cite
APA
ACM
ACS
ABNT
Chicago
Harvard
IEEE
MLA
Turabian
Vancouver
Download Citation
WHAT STUDENTS CAN LEARN FROM FIBONACCI’S ERROR IN SOLVING ‘THE LION IN THE PIT’ PROBLEM
LO QUE PUEDEN APRENDER LOS ESTUDIANTES A PARTIR DEL ERROR DE FIBONACCI AL RESOLVER EL PROBLEMA “EL LEÓN EN EL POZO”
O QUE OS ALUNOS PODEM APRENDER COM O ERRO DE FIBONACCI AO RESOLVER O PROBLEMA "O LEÃO NO POÇO"
Josip Slisko*
Citation: Slisko, J. (2020). What students can learn from Fibonacci’s error in solving ‘The lion in the pit’ problem. Gdola, ensenza y aprendizaje de las ciencias, 15(2), 216-238. DOI: http://doi.org/10.14483/23464712.16041
Recieved: march 03 2020; accepted: march 13 2020
* Ph.D. in philosophy of physics and is a full professor of the Facultad de Ciencias Físico Matemáticas, Benemérita Universidad Autónoma de Puebla, México. He is member of the National System of Researchers (level II). He is interested in students’ construction of explanatory and predictive models of physical phenomena, and their struggles to overcome ‘fast thinking’ in solving mathematical puzzles. Since 1993, he has been organizing the international workshop ‘New Trends in Physics Teaching’. Email: jslisko@fcfm.buap.mx
Abstract
This initial study presents the results of the classroom implementation of a learning sequence derived from Fibonacci’s error in solving ‘The lion in the pit’ problem. The study was carried out with 35 physics students in a general first-semester course ‘Development of complex-thinking skills’. The learning sequence was implemented as a paper-and-pencil activity in personal and group modes. The most important results are the following: (a) Students were able to provide an acceptable procedure about how Fibonacci might get the wrong answer, (b) students can argue why that answer is wrong, (c) some students’ solutions presented good conceptual and procedural clarity, frequently missed in historic literature, and (d) students grasped the importance of knowing about errors made by famous mathematicians in two connected aspects: mathematics is a human activity prone to errors and, consequently, fear of errors shouldn’t be an obstacle in learning of school mathematics.
Keywords: Fibonacci’s error; using history of mathematics in classrooms; learning from errors; problem-solving.
Resumen
Este estudio presenta los resultados de la implementación en el aula de una secuencia de aprendizaje derivada del error de Fibonacci al resolver el problema "El león en el pozo". El estudio se realizó con 35 estudiantes de física en un curso general de primer semestre titulado "Desarrollo de habilidades de pensamiento complejo". La secuencia de aprendizaje se implementó como una actividad de lápiz y papel en modos personales y grupales. Los resultados más importantes son los siguientes: (a) Los estudiantes pudieron proporcionar un procedimiento aceptable sobre cómo Fibonacci podría obtener la respuesta incorrecta; (b) los estudiantes pudieron argumentar por qué esa respuesta es incorrecta; (c) las soluciones de algunos estudiantes presentaron un buen concepto y claridad del procedimiento, frecuentemente omitida en la literatura histórica, y (d) los estudiantes comprendieron la importancia de conocer los errores cometidos por matemáticos famosos en dos aspectos relacionados: las matemáticas son una actividad humana propensa a errores y, en consecuencia, el miedo a los errores no debe ser un obstáculo para el aprendizaje de las matemáticas escolares.
Palabras clave: error de Fibonacci; uso de la historia de las matemáticas en las aulas; aprendizaje a partir de errores; resolución de problemas.
Resumo
Este estudo apresenta os resultados da implementação em sala de aula de uma sequência de aprendizado derivada do erro de Fibonacci na resolução do problema "O leão no poço". O estudo foi realizado com 35 estudantes de física numa disciplina geral do primeiro semestre nomeada "Desenvolvimento de habilidades complexas de pensamento". A sequência de aprendizado foi implementada como uma atividade de lápis e papel nos modos pessoal e coletivo. Os resultados mais importantes são os seguintes: (a) Os alunos foram capazes de fornecer um procedimento aceitável sobre como Fibonacci poderia chegar na resposta errada; (b) os alunos podem argumentar por que essa resposta está errada; (c) as soluções de alguns alunos apresentam um bom conceito e clareza do procedimento, freqüentemente omitido na literatura histórica; e (d) os alunos entenderam a importância de conhecer os erros cometidos por matemáticos famosos em dois aspectos relacionados: a matemática é uma atividade humana propensa a erros e, consequentemente, o medo de erros não deve ser um obstáculo para o aprendizado da matemática na escola.
Palavras-chave: O erro de Fibonacci; uso da história da matemática em sala de aula; aprendendo com os erros; solução de problemas.
Introduction
Danish physicist Niels Bohr, according to scientists’ folklore, defined an expert as follows: ‘An expert is a man who has made all the mistakes which can be made in a very narrow field.’ It may be reformulated by adding an important aspect of expertise and stressing gender neutrality: ‘An expert is a person who has made and self-corrected all the mistakes which can be made in a very narrow field’. This conception of dialogical interplay of making mistakes and gaining knowledge by correcting them becomes important both in industry and education.
Knowing causes and reducing the impacts of human errors in today’s complicated technological systems are priority tasks for many experts in risk management (Reason, 1990; Kletz, 2001; Woods et al., 2010; Dekker, 2014; Taylor, 2016; Strauch, 2017). Bauer, Harteis (2012 p. V) rightly stressed:
Human fallibility is a particular source for practicebased learning. Specifically, learning from errors has become an issue of increased and widespread interest and recognition, as complexity becomes a crucial feature of various domains of daily life: business, society, education…. Two insights are now accepted as features of these domains. Firstly, complex problems and fuzzy rules shape an environment of human behavior which makes errors unavoidable; and, secondly, errors can be fruitful incidents for further development. Hence, contemporary life on the one hand offers the increased prospect of human fallibility, but, on the other hand, provides a rich source for (lifelong) learning.
Metcalfe (2017 p. 468), in her review article ‘Learning from errors’, expressed a strong recommendation: “In comparison with approaches that stress error avoidance, making training more challenging by allowing false starts and errors followed by feedback, discussion, and correction may ultimately lead to better and more flexible transfer of skills to later critical situations”.
For such training, it is important to establish a ‘constructive error climate’ in the classroom:
Although making errors while learning is common, it is also frequently perceived by students as something negative, shameful and is experienced as a potential threat to self-worth. These perceptions often prevent students from regarding errors as learning opportunities. The result is that the potential to learn from them – which is inherent to errors – is not being realized. However, a favorable error climate can support learning from errors and hence foster learning progress. (Steuer, Dresel, 2015 p. 262)
Recently, this approach is gaining support in mathematics education. ‘Error reflection’ is among evidence-based cognitive principles that positively affect mathematics learning: “Thinking about errors improves problem representation and increases conceptual understanding” (Booth et al., 2017 p. 299).
Fear of making errors is one cause of math anxiety. Arem (2010) formulated a list of ‘legitimate math rights’ that help in overcoming adverse affective phenomena often present in mathematics education. That list includes the following: “I have the right to make mistakes in math and to learn from those mistakes” (Arem, 2010 p. 73).
In the Chapter ‘Why we should love mistakes, struggle, and even failure’ of her last book ‘Limitless Mind’, Joe Boaler (2019 p. 56) gave a neuroscience argument for the ‘right to err’: “The times when we are struggling and making mistakes are the best times for brain growth”.
The same message is sent to children in a cartoon book about the brain: “Making mistakes is one of the best ways your brain learns and grows” (Deak, 2000 p. 22).
To promote learning from errors, teachers should induce students to positive and adaptive affectivemotivational reactions to errors. In other words, students should be able to maintain positive emotions and high motivation to learn when faced with mistakes (Matteucci, Soncini, Ciani, 2019).
For such an approach, presenting examples of errors made by mathematicians through history might be useful. Currently, proposals for using history in mathematics learning very rarely mention the role of mistakes.
1. The History of Teaching and Learning Mathematics
Numerous books consider many aspects of historical episodes and materials in teaching and learning mathematics (Katz, 2000; Fauvel, Van Maanen, 2002; Radford, Furinghetti, Hausberger, 2016; Clark et al., 2018). They show that the field is very active and potentially useful for improving how mathematics is taught and learned.
Moreover, various journal articles consider related philosophical, epistemological and pedagogical issues. Some are focused on a single aspect, whereas others take a broader view.
Among the latter, Jankvist’s prominent article on ‘whys’ and ‘hows’ of using history in mathematics education introduces fundamental notions of ‘history as a tool’ and ‘history as a goal’ (Jankvist, 2009). History is seen as a ‘tool’ when it assists in actual learning and teaching of mathematics. History is a goal in itself if it is used for teaching and learning the historical development of mathematics.
More often than not, authors treat only one specific aspect of the history of mathematics. Katz, for example, sees the study of history of a particular curriculum topic as useful for finding valuable pedagogical ideas (Katz, 1986).
In his many writings, Swetz argued for using historical mathematical problems in classrooms to enrich learning (Swetz, 1989) and for giving mathematics the missing social and epistemological relevance (Swetz, 1984). His well-stated arguments deserve citation:
A more direct approach to historically enriching mathematics instruction and the learning of mathematics is to have students solve some of the problems that interested early mathematicians. Such problems offer case studies of many contemporary topics encountered by students in class. They transport the reader back to the age when the problems were posed and illustrate the mathematical concerns of the period.
Often, these same concerns occupy modernday mathematical students. This simple realization, namely, the continuity of mathematical concepts and processes over past centuries, can help motivate learning. Students can experience certain thrill and satisfaction in solving problems that originated centuries ago. In a sense, these problems allow the students to touch the past. (Swetz, 1989 p. 370)
Swetz called attention to art students that commonly visit art museums to gain an appreciation for artist’s techniques: mastery of colour, the interplay of light and shadow, and even the significance of the scenes depicted. In such an approach, both cognitive and affective learning take place. His proposal is the following:
Students can also admire mathematical problems from history, as expressions of human genius. But unlike of museum pieces, these problems can be possessed by viewers through a participation in the solution processes. Questions originating hundreds or even thousands years ago can be understood – and answered in today’s classroom. What a dramatic realization that is! (Swetz, 1989 p. 376)
Swetz also argued that common teaching practices, without a historical perspective, impose on students a notion of mathematical cultural irrelevance:
We frequently find ourselves concentrating on the teaching of “mathematics” – the symbols, the mechanics, the answer-resulting procedures – without really teaching what mathematics is “all about” – where it comes from, how it was labored on, how ideas were perceived, refined, and developed into useful theories – in brief, its social and human relevance. At best, this practice will produce knowledgeable technicians who can dispassionately use mathematics, but it will also produce students who perceive mathematics as an incomprehensible collection of rules and formulas that appear en mass and threateningly descend on them. (Swetz, 1984 p. 54)
Many authors have summarised arguments in favour of using history in mathematics education. Fauvel (1991 p. 4) gave an impressive list of 15 reasons:
(1) Helps to increase motivation for learning; (2) Gives mathematics a human face; (3) Historical development helps to order the presentation of topics in the curriculum; (4) Showing pupils how concepts have developed helps their understanding; (5) Changes pupils’ perceptions of mathematics; (6) Comparing ancient and modern establishes the value of modern techniques; (7) Helps to develop a multicultural approach (8) Provides opportunities for investigations; (9) Past obstacles to development help to explain what today’s pupils find hard; (10) Pupils derive comfort from realizing that they are not the only ones with problems; (11) Encourages quicker learners to look further; (12) Helps to explain the role of mathematics in society; (13) Makes mathematics less frightening; (14) Exploring history helps to sustain your own interest and excitement in mathematics; (15) Provides an opportunity for cross-curricular work with other teachers or subjects.
Liu (2003 p. 416) summarised that list, reducing it to five arguments, which should be a basic panoramic guide for interested mathematics teachers:
1. History can help increase motivation and helps develop a positive attitude toward learning.
2. Past obstacles in the development of mathematics can help explain what today’s students find difficult.
3. Historical problems can help develop students’ mathematical thinking.
4. History reveals the humanistic facets of mathematical knowledge.
5. History gives teachers a guide for teaching.
Liu’s fourth argument, related to human nature of doing and knowing mathematics, one of the objectives of the present paper, is among the most popular in teachers’ journal writings. For example, Marshall and Rich said the following: “History has a vital role to play in today’s mathematics classrooms. It allows students and teachers to think and talk about mathematics in meaningful ways. It demythologizes mathematics by showing that it is the creation of human beings” (Marshall, Rich, 2000 p. 706).
In promoting this view, Marshall and Rich created a web site with historical information. According to one teacher, the site was visited and used in different ways for mathematical projects carried out by 28 middle-school students. Students enjoyed working on the Internet and found it gratifying, challenging and educational (Marshall, Rich, 2000).
Another argument for ‘humanising’ mathematicians was given by Lighter (2000 p. 696):
We often study the published works of the great mathematicians, accept them, and use them gratefully as we solve our problems and delve into the abstractions of our chosen field of mathematics. But rarely do we realize that all these developments were the products of human minds. Mathematicians, indeed, are quite human, and they are not always serious! Their lives are full of interesting twists, turns, and quirks that make them all the more human.
This paper is related to a particular ‘human feature’ of Fibonacci (being prone to error), and it is useful to know what Lighter wrote to ‘humanise’ this famous mathematician:
He often signed his name Leonardo Bigollo. Bigollo meant both traveler and blockhead, and Fibonacci may have meant to convey that he was a great traveler, which he was. Or he may have taken glee in calling himself a blockhead, which many of his contemporaries considered him, and then proving them wrong through his many significant accomplishments. (Lighter, 2000 p. 696)
Taking into account the influence of mathematical textbooks in shaping teaching and learning, one possible way to sway teachers’ pedagogical thinking and practice related to using history is to include historyrelated information into textbooks. Many research articles analyse the quantity and quality of history included in mathematics textbooks (Park, Jang, 2015; Chang, 2015; Ju, Moon, Song, 2016; Schorcht, 2018).
This paper was partially inspired by Chapter 7 of the large ICMI Study ‘History in Mathematics Education’ (Fauvel, Van Maanen, 2002). In that chapter, teachers and researchers are encouraged to take ‘advantage of errors, alternative conceptions, change of perspective, revision of implicit assumptions and intuitive arguments’. One potentially useful example of using a particular error from history was the following:
A surviving deed from Edfu in Egypt, dating back to the 2nd century BC, gave the area of a quadrilateral as the product of the pairs of arithmetic means of opposite sides. From this the area of a triangle was deduced, as the product of the mean of two sides and one half of the third side. Students can be asked to investigate how good the formula is, when it will give a correct answer and what some special cases yield. (Fauvel, Van Maanen, 2000 p. 220)
In comparison with the error above, an error used in research is more relevant in, at least, four aspects: (1) Although the author of the deed above is nameless, the research errors’ author is Fibonacci, a famous mathematician from the XIII century. (2) The same error can be found in many mathematics books written by leading mathematicians over a long period. (3) Its correction was not an easy task for mathematicians and historians of mathematics. Even today, some of them continue to offer an incorrect solution. (4) Students can find correct solutions.
2. Fibonacci’s Error: From its Repetitions to its Corrections
The problem is based on the upward and downward motions of a lion, which was solved incorrectly by Fibonacci. It had various previous formulations with a similar mathematical structure. Sandford connected it with the problem that appeared in the work of the Hindu mathematician Mahavira around 850 of Christian era:
In the course of 3/7 of a day, a ship goes over 1/5 of a krosá in the ocean; being opposed by the wind she goes back during the same time 1/9 of a krosá. Give out, O you who have powerful arms in crossing over the ocean of numbers well, in what time ship will have gone over 99 2/5 krosá? (Sanford, 1951)
The problem was introduced into European mathematics by Fibonacci in his famous book «Liber Abaci», published in 1202 (Sigler, 2002 p. 273):
'On the Lion Who Was in a Pit'
A certain lion is in a certain pit, the depth of which is 50 palms, and he ascends daily 1/7 of a palm, and descends 1/9. It is sought in how many days will he leave the pit’.
Fibonacci’s solution was the following:
You put it that he will leave the pit in 63 days be-cause 63 is the least common multiple of the 9 and the 7, and you see how far the lion ascends and descends in the 63 days; he ascends indeed 63 sevenths palms that are 9 palms, and he descends 63 ninths that are 7 palms which you subtract from the 9, and there remain 2 palms, and this amount he ascends more than he descends in the 63 days.
Thence you say, for the 63 days that I put, he ascends 2 palms; what shall I put so that he ascends 50 palms? You multiply the 63 by the 50, and you divide by the 2; the quotient will be 1575 days, and in this amount of days the lion will leave the pit.
It is not hard to see that Fibonacci found the wrong, ‘quick’ answer, after which the lion comes to the edge of the pit only after the last 1575th descent. In other words, Fibonacci, as many of todays’ pupils and students, used an implicit and impossible assumption of a ‘flying lion’.
The correct solution is found by grasping first that the lion should reach the top not from above (by descending!) but from below (by ascending). To calculate the number of «an-ascent-followed-by-adescent», one has to subtract from the total depth of the pit (50 palms = 3150/63 palms) the daily ascent of the last day (1/7 cubits = 9/63 cubits). In this way, «a modified depth» of 3141/63 palms is obtained. That number is divided by the total rise per day equal to 2/63, resulting in 1570.5 ascents and descents.
However, the number of ascents and descents that happen before the last climb must be an integer. It follows that, before the last climb, 1571 full ascents and descents had to occur. In that time, the lion climbed to a height of 3,142/63 cubits. During the last, 1,572nd day, the lion will only climb an additional 8/63 cubits (out of a possible 9/63 cubits). Thus, the exact solution is ‘1571 8/9 days’ or approximately 1572 days.
As Singmaster has shown (Singmaster, 2004), Fibonacci’s wrong solution, based on missing appropriate treatment «end effect», has been repeated by many mathematicians for several centuries. Among them was Jacopo da Firenze, who, in 1307, one century after Fibonacci, made the same error (Høyrup, 2007). His formulation and solution were the following:
A tower … is 30 braccia high. And at the foot of the said tower there is a serpent, which wants to climb to the top of the tower. And each day it climbs toward the top one third of braccio. And in the night, it descends ¼. I want to know in how much time it will have climbed to the top of the said tower. Do this, and say, 1/3 and ¼ one finds in 12. And then say, the 1/3 of 12 is 4, that is, that they are 4/12. And then say, the ¼ of 12 is 3, that is, 3/12. So that, as… you see, the serpent climbs the day 4/12 of braccio. And in the night it descends 3/12, so that in all it comes to acquire in day and night together 1/12 of braccio. And in 12 days with the nights it comes to climb one braccio. Now if you want to know in how much (time) it will be on the peak a of which we said to be braccia 30 high, then multiply 12 times 30, which makes 360. And in 360 days and nights together it will have climbed on top of the tower. (Høyrup, 2007 pp. 287–288)
As one can easily see, Jacopo replaced the well by a tower, the lion by a snake and changed the rates of climbing and descending. He also defined climbing as an upward motion during the day and descending as a downward motion during the night.
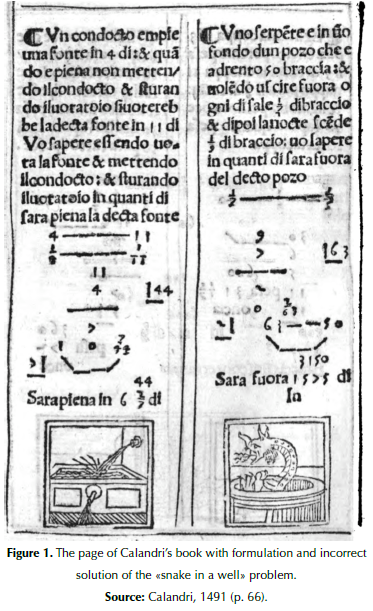
Calandri (1491, p. 66) combined Fibonacci’s and Jacopo’s formulations. From Fibonacci, he ‘borrowed’ the well, its depth and rates of ascending and descending. From Jacopo, he ‘borrowed’ the snake and upward motions during the day and downward motions at night. A new feature was a drawing that complemented the problem formulation (Figure 1). Calandri did not give a long verbal description of the solving procedure, as Fibonacci and Jacopo did. Instead, the readers had to infer the procedure from three number and schematic illustrations. The result was given verbally: The snake will be out after 1575 days.
Paolo Dagomari di Prato, known also as Paolo del' Abbaco, was one of the best XIV century mathematicians in Florence. He became the first author to solve Fibonacci’s problem in two ways: by using the old erroneous way of Fibonacci and by proposing a novel one leading to the correct solution:
There is a well which is 30 braccia deep. Inside lives a serpent which wants to get outside and climbs up every day 2/3 of a braccio and slips down every night 1/5 of a braccio. It is asked in how many days it will be outside of the well. Do as such: subtract 1/5 from 2/3, there remains 7/15, and then you can say, to climb up to the exit, there remains 7/15 of a braccio to climb per day. And thus say as such: if one day is worth 7/15, how much you have in 30? And thus multiply 1 with 30, and it makes 30, and divide by 7/15; do as such: bring 30 to a fifteenfold which is 450, divide it by 7, and what results is 64 2/7, and you have that in 64 and 2/7 days it will be 30 braccia. And it is done.
But note that this calculation can be posed more easily in this way and say as such: how much climbs this serpent in 63 days? Answer that it climbs 29 braccio 2/5 and now say: 3/5 of a braccio is missing, in how much time can it climb 3/5 of a braccio? And therefore say: if 2/3 of a braccio is worth one day, how much will be worth 3/5? Multiply one with 3/5, it makes 3/5, and divide in 2/3, what results in 9/10, and therefore you have that in 9/10 days it climbs 3/5 of a braccio. Therefore you can say that this serpent climbs 30 braccia in 63 9/10 days. And it is true that because of that, the last day we don’t need to climb 1/5 of a braccio, because nothing is added at night, also not having to calculate the ascend of that time, as the ascend not happened. And it is done as you see in 63 9/10 days. And observing this calculation, you see the shortcomings of the errors committed in the other calculation. (Dell'Abbaco, 1964 pp. 151-153).
It is important to note that Dell'Abbaco gave no conceptual and procedure reason why one should look at the height of the snake after 63 days (and nights) and not after, for instance, 62 days and nights.
In 1522, the German mathematician Adam Ries published his famous book «Rechnung auff der Linihen und Federn” that, over centuries, had an impressive number of 108 editions. In that book, Ries reformulated, for the first time, Fibonacci’s problem for the upward and downward movements of a snail (Deschauer, 2013 p. 107): “A snail is 32 yards deep in a well. She climbs 4 2/3 of a yard every day and falls back 3 ¾ of yard every night. In how many days will she come out?”.
Ries first expressed the rise as 14/3 of a yard and the descent as 15/4 of a yard. Then, he wrote both fractions in the form with the same denominator: 56/12 of a yard and 45/12 of a yard. Their difference was 11/12 of a yard, and this represented a total rise during one day and one night.
Subsequently, Ries also expressed the well depth of 32 yards in twelfths: 384/12 yards. In the next step, he took into account boundary conditions (the «end effect» in Singmaster’s terminology), but instead of subtracting the last day rise of 56/12 of a yard from 384/12 of yard, he subtracted the 45/12 of a yard (a night-time descent). Doing so, Ries got a «modified depth» of 339/12 of a yard. To obtain the number of days (and nights) required, Ries divided the «modified depth» by a total day-and-night rise of 11/12 of a yard. In this way, the solution obtained by Ries was 30 9/11 days. In other words, the snail will exit the well after 9/11 has passed since the last day.
The Ries procedure was a step in the right direction, but his ‘30 9/11 days’ solution was wrong because he did not take away the daily rise from the total well depth but the night descent. In 1525, Ries published the second edition of his arithmetic book (Figure 2).
It that book, Ries came up with the correct solution ‘30 54/56 days’ but also used a conceptually incorrect procedure for it.
As before, he first subtracted from the initial depth (384/12 yards) one night’s descent (45/12 yards). After that, Ries divided a modified depth (339/12 yards) with a total day–night rise (11/12 yards). The round-number amount of day and night motions was 30. During this time, the snail realised complete climbs and descents. Lastly, Ries added ad hoc one night’s lowering of 45/12 yards to the rest of 9/12 of a yard. He interpreted the result 54/12 as the distance the snail would traverse in the last climb. The result was written in the form ‘30 27/28 days’.

The conceptually correct way to perform this solution is as follows: Modified depth (328/12 yards) is obtained by subtracting the last daily climb (56/12 yards) from the initial depth (384/12 yards). When the modified depth (328/12) is divided by the day– night rise (11/12 of a yard), the result is 29.818 days and nights. However, such a mathematical result is impossible in the real world because it implies that after 0.813 of a rise, 0.818 of a fall follows. Incomplete rise and fall contradict the nature of motions supposed in the problem. Thirty complete days and nights must pass before the last climb. During this time, the snail climbs 330/12 yards. On the last day, the snail does not have to climb 56/12 but only 54/12 yards. In that way, the snail will spend 54/56 or 27/28 of the last and 31st day for his final climb.
3. A Review of Secondary Literature on Fibonacci’s Problem and its Posterior Reformulations
One of the most popular problems from Fibonacci’s book ‘Liber Abaci’ is the following:
‘On Two Men Having Bread.
There were two men, the first of whom had 3 loaves of bread and the other 2 loaves, and they took a walk to a certain fountain where they met together sitting and eating, and a soldier passed by; they invited him to join them, and he sat down and ate with them, and when they had eaten all the bread the soldier departed leaving them 5 bezants for his share. Of this the first took 3 bezants as he had 3 loaves; the other truly took the other two bezants for his two loaves. It is sought whether the division was just or not.
A certain person asserted that the division was correct as each had one bezant, for each loaf, but this is false because the three ate all five loaves. Whence each took 1 2/3 loaves; the soldier ate 1 1/3 loaves, that is 4/3 from the loaves which the three had. Of the loaves truly the other ate only so much as 1/3 of one loaf. Therefore the first man took 4 bezants and the other 1 bezant. (Sigler, 2002 pp. 403-404)
Laurence Sigler, translator of ‘Liber Abaci’ into English, wrote a long critical comment on Fibonacci’s solution:
The end of this problem is murky. It is said that each of the three take 5/3 of a loaf, but the remark about the soldier's eating 4/3 of a loaf and the second man’s eating 1/3 of a loaf is not clear. How much did the first man eat? The monetary answer given of 4 bezants for the first man and 1 bezant for the second could possibly be obtained with the following reasoning. The first man contributed 3 loaves of bread and ate 5/3 loaves. The second man contributed 2 loaves and ate 5/3 loaves. Valuing the bread at one bezant per loaf because the soldier gave 5 bezants presumably for 5 loaves, the first man had an excess of 4/3 bezant, contribution minus consumption. The second man had an excess of 1/3 bezant, contribution minus consumption. Since the ratio is 4/3 to 1/3 or 4 to 1, the first man should take 4 bezants and the second 1 bezant. (Sigler, 2002, comment 24 on the Chapter 12, p. 627)
Taking into account this comment and the fact that Sigler corrected many minor errors in his translation of Fibonacci’s book, it is rather surprising that he did not notice that Fibonacci’s solution to ‘Lion in a pit’ was erroneous.
Sigler was not the only mathematician who failed to detect the error in Fibonacci’s solution. Vera Sanford mentioned the problem three times (Sanford, 1951, 1958, 1972). Only once, she presented a summary of Fibonacci’s solution: “Since the lion climbs one palm in seven days, and descends one palm in nine days, in sixty three days he will climb two palms. Therefore to climb 50 palms, he will require 63 × 25 or 1575 days” (Sanford, 1972 p. 63).
She did not say that the solution is wrong.
Mathematicians have commented that Fibonacci made a mistake and provided a correct solution. One of them is Victor J. Katz:
Another classic problem is that of the lion in the pit:
The pit is 50 feet deep. The lion climbs up 1/7 of a foot each day and then falls back 1/9 of a foot each night. How long will it take him to climb out of the pit?
Leonardo here used a version of ‘false position’. He assumed the answer to be 63 days, since 63 is divisible by both 7 and 9. Thus, in 63 days the lion will climb up 9 feet and fall down 7, for a net gain of 2 feet. By proportionality, then, to climb 50 feet, the lion will take 1575 days.
(By the way, Leonardo’s answer is incorrect. At the end of 1571 days, the lion will be 8/63 of a foot from the top. On the next day, he will reach the top.) (Katz, 2009 p. 44)
Katz’s approach was taken over by Petkovic (2009). He also first presented the problem:
A lion trapped in a pit 50 feet deep tries to climb out of it. Each day he climbs up 1/7 of a foot, but each night slips back 1/9 of a foot. How many days will it take the lion to reach the top of the pit?’ (Petkovic, 2009, Problem 11.9, p. 284).
In the footnote, Petkovic, following Katz, said the following:
Fibonacci, by the way, gave a false solution…. He started from 63 as a number divisible by both 7 and 9 and found that in 63 days the lion would climb up 9 feet and fall down 7. Hence, the lion advances 2 feet every day (should be 63 days, J.S) and, by proportionality, he calculated that the lion would take (50 : 2) × 63 = 1575 days to climb the 50 feet to reach the top of the pit. The correct answer is 1572 days; actually, the lion will be only 8/63 of a foot from the top at the end of 1571 days, so that he will reach the top all the next day. (Petkovic, 2009 p. 284)
It is important to note that, neither Katz nor Petkovic, gave an argument why the position of the lion was calculated after 1571 days and not, for example, after 1570 days. In addition, a pedantic comment regarding historical accuracy
– Fibonacci did not define descents as motions during nights.
As Fibonacci, Swetz (2012) didn’t connect downward lion’s motions with night: “There is a lion in a well whose depth is 50 palms. He climbs 1/7 of a palm daily and slips back 1/9 of a palm. In how many days will he get out of the well?” (Swetz, 2012, Chapter 9 ‘Medieval Europe’, Problem 2, p. 87).
Nevertheless, he did not mention the authorship of the problem. Swetz gave a solution of ‘1,572 days’ (Swetz, 2012 p. 171), without saying that original solution ‘1,575 days’ was erroneous.
David Singmaster’s monumental work ‘Assorted Articles on Recreational Mathematics and the History of Mathematics’ can be found at the webpage of The Puzzle Museum (www.puzlemuseum.com) in the section on ‘Sources in Recreational Mathematics’ (Figure 3).
There, he provided an exhaustive revision of literature related to Fibonacci’s problem in Section 10.H. ‘Snail Climbing out of Well’. He gave a general formulation of ‘climbing snail problem’ in this way:
A snail is at the bottom of a well which is D deep. He climbs A in the day and slips back B in the night. How long does it take to get out?
The earlier versions had serpents, snakes and lions. The ‘end effect’ is that when the snail gets to within A of the top, he doesn't slip back.
Singmaster also gave a conceptually correct solution plan:
For convenience, let the net gain per day be G = A - B. The solution is to take the least N such that NG + A = D, i.e. N = (D - A)/G, then interpolate during the daytime of the (N + 1)-st day, getting (D - NG)/A of the day time on the (N + 1)-st day as the time of meeting.
It is strange that Singmaster, when presenting Fibonacci’s formulation of the problem, gave neither Fibonacci’s solution (without the ‘end effect’) nor the correct solution, based on his solution plan. Even more surprising is his presentation of the problem in the case of Calandri (1491): “F. 71v. Serpent in well. +1/7 in the day and -1/9 in the night to go 50. He doesn’t consider the end effect, so gives 1575 instead of 1572 ½”.
Therefore, it seems that Singmaster, correcting Calandri’s (and Fibonacci’s) wrong answer, gave another incorrect answer ‘1572 ½’ as a correct one!
The same issue arose with Høyrup’s ‘correction’ of the wrong answer, ‘360 days (and nights)’, given by Jacopo da Firenze for the snake climbing the tower: “We observe that the dress is not taken very seriously: at the end of the 356th day, the serpent has reached the top, and we do not need to count the sliding-down in the subsequent night” (Høyrup, 2007 p. 92)
To see that Høyrup’s suggested ‘correct’ solution is wrong, let us find a real correct solution in the case of Jacopo’s formulation of the problem. The serpent climbs 1/3 = 4/12 braccio during the day and descends ¼ = 3/12 braccio during the night. In one whole day-and-night, the serpent rises 1/12 braccio.
Resting that 4/12 from the total height of 30 braccio, one gets height that should be covered by fully climbing and descending: 360/12 braccio - 4/12 braccio = 356/12 braccio.
That height (356/12 = 29 2/3) has been reached in 356 days-and-nights. Consequently, the height of 30 braccio would be reached, not at the end of the 356th day, as suggested by Høyrup, but at the end of the next 357th day.
This section ends by adding one more example of this disturbing phenomenon when somebody ‘corrects’ a wrong answer to the ‘climbing snail’ puzzle by giving another wrong answer. The example comes from a recent published book ‘Games and mathematics. Subtle connections’, written by David Wells, a former Cambridge student, chess champion and prolific author of many popular books on mathematics.
With such a background, nobody would expect that Wells would offer an incorrect answer to his formulation of the snail puzzle (Wells, 2012 p. 4):
Another traditional puzzle appeals to me because it sets the solver a trap, albeit
a rather obvious one. Here is one version. A snail
— or a serpent or a frog! — lies
at the bottom of a well, 30 units deep. It climbs 6 units every day but falls back
3 units every night. How long does it take to escape from the well?
The obvious answer is that the snail rises 3 units every day-and-night, on balance, so it takes 10 daysand-nights to escape, but this is wrong because it will actually reach the top of the well half-way through the 10th day and after only 9 nights’.
Wells’ likely solution strategy is as follows: In 9 days-and-nights, the snail rises 27 units (9 × 3). During half of the 10th day, he will climb missing 3 units.
Nevertheless, a correct answer is different. The snail should come to the top after the-last-day 6-unit climb. The rest (30 units - 6 units = 24 units) should have been covered in a climbing-and-falling manner: 3 units per day-and-night. As 24/4 = 8, for eight days and eight nights, the snail would climb up to 24 units, and during the ninth day, after climbing the missing 6 units, it would reach the top. Therefore, the snail would need 9 whole days and 8 whole nights, not 10 and half days and 9 whole nights, as suggested by Wells.
4. Previous Experimental Studies with Fibonacci’s Problems
Sullivan, Panasuk (1997) used a mathematical puzzle that asks about the ‘missing’ area and leads to an exploration of the Fibonacci sequence to design and implement a genuine students’ inquiry whose aim was to connect plane geometry to algebra. They described and discussed the inquiry, the concepts, the solution and an extension that deepened all students’ understanding of connections between algebra and geometry.
Taskin et al. (2013 p. 171) used Fibonacci’s ‘Two towers and two birds’ problem to explore students’ abilities in applying Polya’s four steps in problemsolving. The selected problem had the following formulation:
Two towers, the heights of which are 30 paces and 40 paces, have a 50 paces distance. Between the two towers, there is a font where two birds, flying down from the two towers at the same speed will arrive at the same time. What is the distance of the font from the two towers?
The worksheet was composed of 11 tasks. The first five tasks were about understanding the problem. The task asked for a solution plan, the 7th was about carrying out the plan, and the 8th, 9th and 10th tasks were about looking back. Finally, the 11th task asked students to pose a new problem. The study was implemented with 28 ninth-grade students.
The study showed that students had difficulties understanding the problem because it was given verbally, and the solution depends critically on students’ visualisation skills. The other difficulty was related to the evaluation of the obtained result.
Although the outcome of this research is rather negative, the authors suggest that they should use historical problems and Polya’s problem-solving steps as group activities.
Gil, Martinho (2016) used the same Fibonacci’s ‘two towers’ problem to foster eighth-grade students’ arguing skills. They found that students used different types of arguments that showed different degrees of formality and kinds of reasoning. Students expressed and justified their ideas and interpreted and understood opinions presented to them. Gil, Martinho concluded that the history of mathematics proved to be an enabling tool for mathematics learning, particularly for building a community of mathematical discourse, in which mathematical disagreement was reflected.
Juárez, Hernández, Slisko (2014) explored junior high-school students’ performance in solving Fibonacci’s ‘Two travellers’ problem. The 44 students who successfully participated in the study (completing tasks in the worksheet) were training for a Mathematical Olympiad. The worksheet used was the following:
Two travellers
There are two men who propose to go on a long journey, and one will go 20 miles daily. The other truly goes 1 mile the first day, 2 miles second, 3 miles third, and so on, always one more mile daily to the end when they meet. How many days does a second man need to reach the first one?
a. Describe only in words (without using formulas or mathematical expressions) the plan you have to solve the problem.
b. Carry out the plan mathematically.
c. Your solution is: The second traveller reaches the first one after _____ days.
d. Show below that your solution is correct.
Some students were able to apply the Gauss formula and solved the problem through an algebraic approach. Other students were able to grasp a simple, symmetric feature of the problem situation that permits an easy arithmetic solution without using algebra. Therefore, these students, in a sense, outperformed Fibonacci!
By contrast, some students showed poor understanding of the problem and made calculation errors not expected from student’s who want to participate in a Mathematical Olympiad.
A very complex study using Fibonacci’s problems with pre-university students was designed and carried out by Marc Moyon in France (2019). Students first solved the following problem:
A certain man entered a certain pleasure garden through 7 doors, and he took from there a number of apples; when he wished to leave he had to give the first doorkeeper half of all the apples and one more; to the second doorkeeper he gave half of the remaining apples and one more. He gave to the other 5 doorkeepers similarly, and there was one apple left for him. It is sought how many apples there were that he collected.
After that, they were given Fibonacci’s algorithmic solution for discussion. Then, students were asked to solve a structurally similar problem in which the man had one apple left after passing 457 doors.
Finally, students compared the ‘Apple orchard problem’ with Fibonacci’s ‘A man on business’ problem:
A certain man went on business to Lucca to make a profit doubled his money, and he spent there 12 denari. He then left and went through Florence; he there doubled his money, and spent 12 denari. Then he returned to Pisa, doubled his money and it is proposed that he had nothing left. It is sought how much he had at the beginning.
As an important finding of the study, Moyon reported the following:
When pupils engaged with the source, most of them had questions (on terminology or on mathematical procedures) similar to those a professional historian of mathematics would ask, especially when they compared different historical solutions with their own. It is, for me, a great opportunity to develop the critical thinking of pupils.
5. Objectives and Methodology of this Study
The objectives of this exploration study were to give initial experimental answers to the following research questions:
Are students able to propose a procedure that leads to Fibonacci’s erroneous solution of ‘Lion in a pit’ problem, after being informed that his solution was wrong?
Can students formulate an acceptable plan for finding a correct answer to the Fibonacci’s problem?
Are students able to formulate an acceptable plan…
Are students able to demonstrate that their solution is correct?
What do students conclude after learning about an error made by a famous mathematician?
Thirty-five students enrolled in a general firstsemester course ‘Development of Complex Thinking Skills’ (Slisko, 2017) participated in the study. Their cognitive levels were previously measured by ‘Test of Logical Thinking’ and ‘Cognitive Reflection Test’ (Slisko, 2017).
The study was based on a ‘paper-and-pencil’ questionnaire with two modes of answering questions. Students first provided their answers. Subsequently, students were divided randomly into nine groups. Eight groups had four students and one group three. The questionnaire used in the study is provided in Figure 4.
The personal phase lasted 20 min, and in the group phase, students were given 30 min to discuss previous personal answers and formulate group answers.

6. The Results of this Study
After preliminary consideration, the results of this study are briefly presented for each task, taking into account both personal and group performance.
a. The Solution ‘1,575 days’, Presented by Fibonacci, is Wrong. How Could Fibonacci Have Come to Such an Answer?
In this task, students were not expected to reproduce Fibonacci’s solution. Acceptable performance considered two steps. First, students should have found a daily rise during each day, 1/7 - 1/9 = 2/63. Second, students should have divided 50 (or 3150/63) by 2/63 to arrive at 1575 as the number of days. One example of an acceptable group solution is as follows:
In one day, the lion covers the distance ![]() The total distance was
The total distance was ![]() .
.
Due to it, (the lion) needed
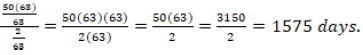
Four groups provided an acceptable solution as a group, having at least one student who was able to find the procedure that leads to Fibonacci’s erroneous answer.
Four groups did not provide an acceptable procedure. Nevertheless, at the personal level, at least one acceptable answer was found. Students with acceptable solutions were not able, during discussions, to ‘sell’ them to the rest of the group.
One group did not come up with an acceptable solution, either on group level or personal level.
b. Why Fibonacci’s Answer is Wrong?
In this task, students were expected to recognise that the problem with Fibonacci’s answer was the ‘flying lion’ defect, i.e., the lion gets to the ground level through the last descent. Acceptable answers were variations of the following:
Because he did not take into account that when the lion was near the final 9/63 of a palm remained to climb, the lion would not need to descend 7/63 palms, because he would be out of the well.
Seven groups had acceptable descriptions, formulating good arguments of why Fibonacci’s solution was wrong.
Two groups did not provide an acceptable description. Their members formulated alternative arguments for incorrectness of Fibonacci’s answer:
‘Because after 1575 days, he would have reached 50 spans, but he would not come out of the well’.
‘Lion size is not taken into account’.
‘1575 days are 4.3 years, a lion trapped in a well,
without food or water would not be able to survive 4 years in those conditions’.‘Because, maybe, the lion doesn’t have to eat and is starving’.
These arguments show that some students question implicit modelling of a lion as a ‘particle-like’ animal or consider real-life restrictions of lion behaviour.
c. Describe Verbally (without Using Mathematical Expressions) your Plan to Find the Correct Answer
In this task, from nine groups, only four had an approximate idea of a possible plan. Plans were more about what should be taken into account or done and less how to do it precisely:
‘We would find the distances that the lion travels during the last days and then we look for a distance to which when advancing 1/7 of a palm exceeds 50 palms’.
‘Analyze the behavior of the lion during the ascent and descent. Pay a special attention to the moment when it is not necessary to go down again’.
‘Find on what day the lion takes approximately 1/7 of a palm to leave the well’.
‘The lion ascends 1/7 of a palm per day and descends 1/9 of a palm. Per day he travels 2/63 of a palm, but on the last day it only ascends 1/7 of a palm and no longer descends because he is already up. Then we subtract this part and see how long it takes to travel the rest. In the end that residue will be added’.
These results were expected, taking into account that verbally planning a solution is not a common activity in problem-solving, at least not in Mexican mathematics and physics pre-university education.
d. Carry Out Your Plan Mathematically
In this task, at a group level, students did not produce a single correct result (1572 days) using a conceptually clear and verbally argued solving procedure. Two groups presented the result using different approaches. The first approach was as follows:
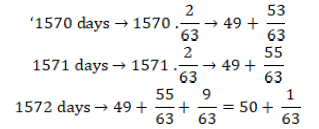
Consequently, 1572 days should pass in order to get out’.
Students in this group realised that on the 1572nd day only climbing should happen. That realisation is likely the reason that in the last numerical line the term ‘+9/63’ appears.
The second approach was as follows:
After 1570 days, the lion still needs
needssums one day. After 1572 days gets free.
This group had a very good start. They found correctly the ‘modified depth’ of the well (49 6/7 palms) and the number of days (1570.5 days) to climb it by rising daily 2/63 of a palm. Instead of rounding up the number of days to 1571 days, they erroneously rounded it down to 1570 days. The correct result of 1572 days was not derived clearly.
Two groups found the result ‘1571.5 days’ again using different but, in deeper view, similar approaches. The first approach was as follows:
As in one day total displacement of the lion is 2/63 palms, then the equation, that describes which time the lion needs to get to the distance y from the surface is:
y = 50 – (2/63)t.
When to the lion remain 1/7 palms for getting out, the number of days is:
1/7 =50 –(2/63) t =1570.5 days
Finally, the lion needs 1-day to move 1/7 palms and get out. Due to it, the lion takes 1571 days and half in getting out.
The second approach was developed as follows:
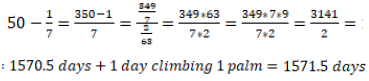
Neglecting catastrophic errors in using the sign ‘=’ in their arithmetical and algebraic expressions, both groups found the mathematically correct time (1570.5 days) needed to climb the ‘modified depth’ of 349/7 palms. To that time, they just added mechanically one more day.
Only one student was able to round up 1570.5 days to 1571 days and to find the correct result:
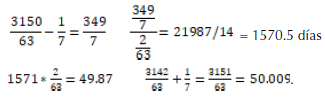
Although the answer was not provided in this task, the student stated in the next task that the result is ‘1572 days’. Again, this student was not able to verbalise adequate arguments to convince his peers that he had the best solution.
In general terms, students were able to get very close to the concept of ‘modified depth’ and corresponding time, which are the first steps toward a conceptually clear approach to the correct solution. This result is very important in light of errors made by experts.
e. To Leave the Well, the Lion Took _________ Days
The space in this task was filled in differently.
Five groups stated their result as ‘1572 days’.
Three groups declared the result as ‘1571.5 days’.
One group had a very strange result of 2280 days’.
One group, who stated their result as ‘1572 days’, is important because, at the individual level, all members of this group stated that the result should be ‘1576 days. They argued that the lion for 1575 days can only reach the edge of the well, needing one extra day (the 1576th one) to get out.
f. Prove that Your Solution is Correct
Only two of five groups with the correct result of ‘1572 days’ presented clear demonstrations:
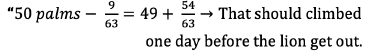
Consequently, as in 1571 days climbs 49 + (55/63), he goes out the next day.
It is correct because in the day 1571(the lion) reached 3142/63 palms. Due to it, if he climbs 1/7 of palm or 9/63 of palm, he will get over 50 palms or 3150/63 palms.
The demonstration presented by the remaining three groups and three groups with the answer ‘1571.5 days were defective, both in conceptual clearness and procedural correctness. One example for ‘1571.5 days’ is as follows:

It is important to note that in this ‘demonstration’, students subtract a time (1 day) from a distance (1571.5)! Mathematics teaching may need to pay more attention to the correct use of units in which quantities are measured and expressed.
The group with the proposed ‘correct’ answer of ‘2280’ did not try to provide a demonstration.
g. Do You Think It’s Good to Know that Even Famous Mathematicians Make Mistakes?
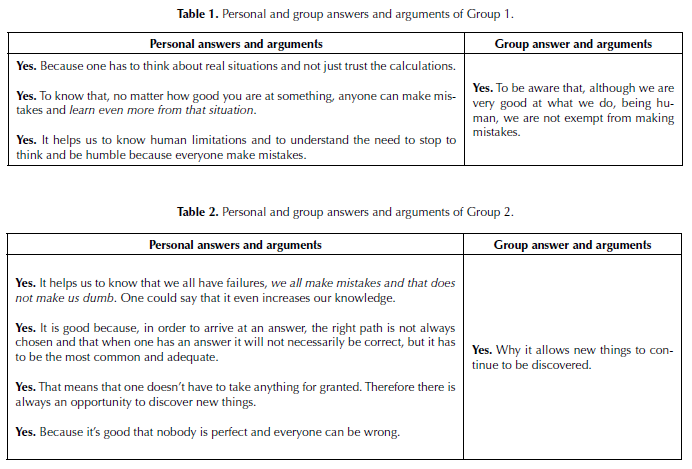
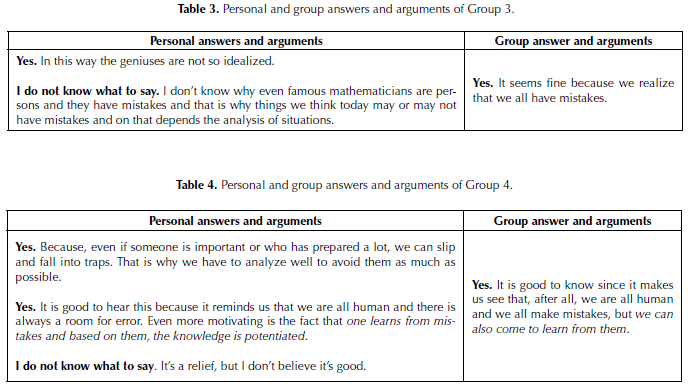
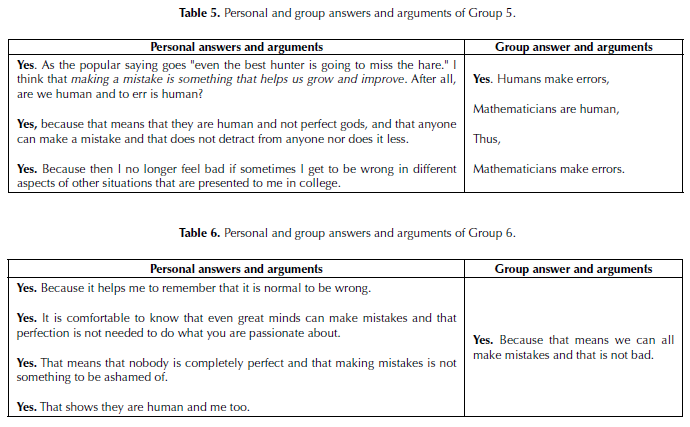
In both personal and group phases, students had an opportunity to select and justify one among offered answers: (A) Yes. (b) No. (c) I don’t know what to say.
From 27 students who provided their selection at a personal level, 24 selected ‘Yes’, and 3 selected ‘I don’t know what to say. At the group level, 8 groups selected ‘Yes’ and only one selected ‘I don’t know what to say’.
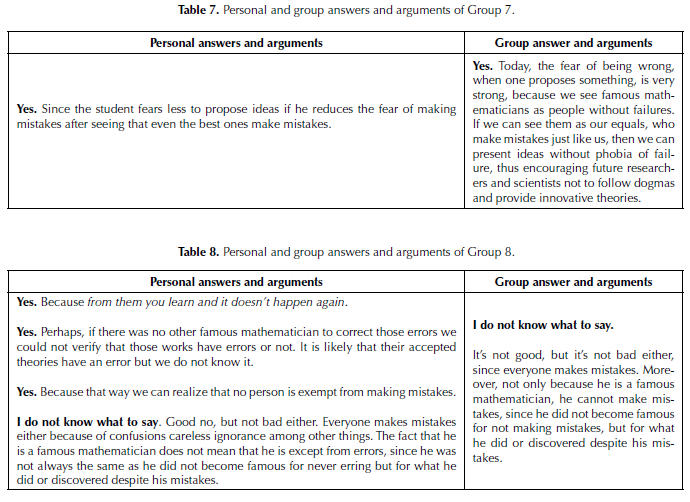
In general terms, students mostly thought that knowing that famous mathematicians make errors is good because it shows that mathematicians are also humans. Nevertheless, a group (Group 7, see the Appendix) provided a far-reaching view on the issue:
Today, the fear of being wrong, when one proposes something, is very strong, because we see famous mathematicians as people without failures. If we can see them as our equals, who make mistakes just like us, then we can present ideas without phobia of failure, thus encouraging future researchers and scientists not to follow dogmas and provide innovative theories.
It is important to stress that this formulation is a group elaboration because on a personal level it was less developed.
The idea of ‘learning from errors’ was mentioned explicitly by four students, but only one group included that idea in its argument. This, in a sense, is a negative result that shows that good personal ideas are not always accepted at group levels. It is likely related to students’ undeveloped personal debating and communication skills that are necessary to convince others that an idea is worth sharing. Such occurs even when others have initially different ideas (see the case of Group 8 in Appendix).
7. Conclusions and Recommendations for Teaching and Research
Initial analysis of the results of this study shows that students are able to find the error in Fibonacci’s solution. Some went much farther. At personal and group levels, they provided a conceptually clear approach to get a correct answer. This result is important because such solution transparency is missing in some expert treatments of the ‘climbing snail problem’.
Moreover, by informing students about Fibonacci’s error, this study induced positive student thinking about (1) the ‘human face’ of mathematicians and (2) a fearless approach to their errors, seeing them as opportunities for learning.
Teachers may wish to inform their students about this or other errors made by mathematicians in the course of history. Especially useful are errors that students can identify and correct. In doing so, students are likely to accept a new ‘error culture’ in which making and correcting errors is seen as a necessary phase in better mathematics learning. Errors should not be a reason for math anxiety but a path to joyful experiences with school mathematics.
To understand why a correct personal idea is not accepted at the group level or why an ‘unpopular’ personal view is accepted as a group view, it is necessary to use a methodology that allows observation of details of students’ group discussions. Another potentially interesting issue is the relationship between students’ cognitive levels and their problem-solving and debating skills.
8. Acknowledgement
I thank to Dr Albrecht Heeffer (Ghent University, Belgium) for translating into English Dall’Abbaco’s solutions for the climbing snake problem, and to my student Miguel Ángel Sandoval for transcribing students’ personal and group hand-written answers.
References
AREM, C. A. Conquering math anxiety. A self-help workbook. Third edition. Brooks/Cole. Belmont, CA. 2010.
BAUER, J.; HARTEIS, C. (eds.). Human Fallibility: The Ambiguity of Errors for Work and Learning. Springer. Dordrecht. 2012. https://doi.org/10.1007/978-90-481-3941-5
BOALER, J. Limitless Mind. Learn, lead, and live without barriers. Harper One. New York. 2019.
BOOTH, J. L. et al. Evidence for cognitive science principles that impact learning in mathematics. In GEARY, D.C. et al. (editors), Acquisition of complex arithmetic skills and higher-order mathematics concepts. Academic Press. Amsterdam. 2017. pp. 297-325. https://doi.org/10.1016/B978-0-12-805086-6.00013-8
CALANDRI, F. De Arithmetica. Lorenzo da Morgiani y GiovanniThedesco da Maganza. Florencia, 1491.
CHANG, H. Analysis on Using the History of Mathematics in Chinese Mathematics Textbooks. Journal for History of Mathematics, Seoul, Korea, v. 28, n. 1, pp. 15-29. 2015. https://doi.org/10.14477/jhm.2015.28.1.015
CLARK, K. M. et al. (editors). Mathematics, Education and History. Towards a harmonious partnership. ICME-13 monographs. Springer. Cham. 2018
DEAK, J. Your fantastic elastic brain. Stretch it, shape it. Little Pickle Press. Belvedere, CA. 2010.
DEKKER, S. The Field Guide to Understanding “Human Error”. Third Edition. Ashgate Publishing Company. Farnham, UK. 2014.
DELL’ABBACO, P. Tratatto d’Aritmetica. Secondo la lezione del Magliabechiano XI, 86 de la Biblioteca Nazionale di Firenze. A cura e con introduzione di Gino Arrighi. Domus Galileana. Pisa. 1964.
DESCHAUER, S. Das zweite Rechenbuch von Adam Ries: eine moderne Textfassung mit Kommentar und metrologischem Anhang und einer Einfrung in Leben und Werk des Rechenmeisters. Springer-Verlag. Berlin. 2013.
FAUVEL, J. Using History in Mathematics Education. For the Learning of Mathematics, Edmonton, Canada, v. 11, n. 2, pp. 3-6. 1991.
FAUVEL, J.; VAN MAANEN, J. (editors). History in Mathematics Education. The ICMI Study. Kluwer Academic Publishers. New York. 2002. https:// doi.org/10.1007/0-306-47220-1
GIL, P., MARTINHO, M. H. The role of history of mathematics in fostering argumentation: Two towers, two birds and a fountain. In CERME 9 - Ninth Congress of the European Society for Research in Mathematics Education, Charles University in Prague, Faculty of Education; ERME, Feb 2015, Prague, Czech Republic. 2016. pp. 1817-1824.
HØYRUP, J. Jacopo da Firenze‘s Tractatus Algorismi and Early Italian Abbacus Culture. Birkhäuser. Basel. 2007. https://doi.org/10.1007/978-3-7643-8391-6
JANKVIST, U. T. A categorization of the “whys” and “hows” of using history in mathematics education. Educational Studies in Mathematics, Heidelberg, Germany, v. 71, n. 3, pp. 235-261. 2009. https://doi.org/10.1007/s10649-008-9174-9
JU, M. K.; MOON, J. E.; SONG, R. J. History of mathematics in Korean mathematics textbooks: Implication for using ethnomathematics in culturally diverse school. International Journal of Science and Mathematics Education, Heidelberg, Germany , v. 14, n. 7, pp. 1321-1338. 2016. https:// doi.org/10.1007/s10763-015-9647-0
JUÁREZ RAMÍREZ, M. A.; HERNÁNDEZ REBOLLAR, L. A.; SLISKO, J. Fibonacci’s motion problem “Two travellers”: The solutions given by junior high-school students who were trained for Mathematical Olympiad. Latin American Journal of Physics Education, Mexico City, v. 8, n. 3, pp. 390-396. 2014.
KATZ, V. (editor). Using History to Teach Mathematics. An International Perspective. The Mathematical Association of America. Washington, D.C. 2000.
KATZ, V. J. A History of Mathematics. An Introduction. Third Edition. Addison-Wesley. Boston. 2009.
KATZ, V. J. Using history in teaching mathematics. For the Learning of Mathematics, C Edmonton, Canada, v. 3, pp. 13-19. 1986.
KLETZ, T. An engineer's view of human error. Third edition. Institution of Chemical Engineers. Rugby, UK. 2001.
LIGHTER, J. Mathematicians are human too. Mathematics Teacher, Washington, D.C., v. 93, n. 8, pp. 696-699. 2000.
LIU, P. H. Do teachers need to incorporate the history of mathematics in their teaching? Mathematics Teacher, Washington, D.C., v. 96, n. 6, pp. 416-421. 2003.
MARSHALL, G. L.; RICH, B. S. The role of history in a mathematics class. The Mathematics Teacher, Washington, D.C., v. 93, n. 8, pp. 704-706. 2000.
MATTEUCCI, M. C.; SONCINI, A.; CIANI, A. From failure to success: The potential beneficial role of error. In: COLUMBUS, A. M. (editor), Advances in Psychology Research. NOVA Science Publishers. New York. 2019. pp. 111-141.
METCALFE, J. Learning from Errors. Annual Review of Psychology, Princeton, n. 68, pp. 465-489. 2017. https://doi.org/10.1146/annurev-psych-010416-044022
MOYON, M. Teaching Mathematics and Algorithmics with Recreational Problems: The Liber Abaci of Fibonacci. In: BARBIN, É. et al. (editors). Proceedings of the Eighth European Summer University on History and Epistemology in mathematics Education (ESU-8) (Skriftserie 2019, nr. 11). Oslo Metropolitan University. Oslo. 2019.
PARK, J.; JANG, D. Study on Criticism and Alternative on the History of Mathematics Described in the Secondary School Mathematics Textbooks. Communications of Mathematical Education, Seoul, Korea, v. 29, n. 2, pp. 157-196. 2015. https://doi.org/10.7468/jksmee.2015.29.2.157
PETKOVIC, M. S. Famous Puzzles of Great Mathematicians. American Mathematical Society. Providence. 2009. https://doi.org/10.1090/mbk/063
RADFORD, L.; FURINGHETTI, F.; HAUSBERGER, T. (editors). Proceedings of the 2016 ICME Satellite Meeting of the International Study Group on the Relations Between the History and Pedagogy of Mathematics. IREM de Montpellier. Montpellier. 2016.
REASON, J. Human Error. Cambridge University Press. Cambridge, UK. 1990.
RIES, A. Rechnung auff der linihen. Maler. Erfurt. 1525.
SANFORD, V. The problem of the lion in the well. The Mathematics Teacher, Washington, D.C., v. 44, n. 3, pp. 196-197. 1951.
SANFORD, V. A Short History of Mathematics. The Riverside Press. Cambridge, MA. 1958. SANFORD, V. The History and Significance of Certain Standard Problems in Algebra. AMS Press. New Work. 1972. This is a reprint edition of original edition published in 1927 by College Press, New York.
SCHORCHT, S. History of Mathematics in German Mathematics Textbooks. In: Clark, K. M. et al. (editors). Mathematics, Education and History. Springer. Cham. 2018. pp. 143-162. https://doi.org/10.1007/978-3-319-73924-3_8
SIGLER, L. E. Fibonacci's Liber Abaci: a translation into modern English of Leonardo Pisano's Book of calculation. Springer. New York. 2002.
SINGMASTER, D. Sources in Recreational Mathematics. An Annotated Bibliography. Eight Preliminary Edition. The Puzzle Museum. London. 2004.
SLISKO, J. Self-Regulated Learning in A General University Course: Design of Learning Tasks, Their Implementation and Measured Cognitive Effects. Journal of European Education, Kayseri, Turkey, v. 7, n. 2, pp. 12-24. 2017.
STEUER, G.; DRESEL, M. A constructive error climate as an element of effective learning environments. Psychological Test and Assessment Modeling, Lengerich, Germany, v. 57, n. 2, pp. 262-275. 2015.
STRAUCH, B. Investigating Human Error: Incidents, Accidents, and Complex Systems. Second Edition. CRC Press. Boca Raton, FL. 2017. https:// doi.org/10.4324/9781315251851
SULLIVAN, M. M.; PANASUK, R. M. Fibonaccinumbers and an area puzzle: Connecting geometry and algebra in the mathematics classroom. School Science and Mathematics, Stillwater, Oklahoma, v. 97, n. 3, pp. 132-138. 1997. https:// doi.org/10.1111/j.1949-8594.1997.tb17356.x
SWETZ, F. J. Seeking relevance? Try the history of mathematics. The Mathematics Teacher, Washington, D. C., v. 77, n. 1, pp. 54-47. 1984.
SWETZ, F. J. Using Problems from the History of Mathematics in Classroom. The Mathematics Teacher, Washington, D. C., v. 82, n. 5, pp. 370-377. 1989.
SWETZ, F. J. Mathematical expeditions: Exploring word problems across the ages. Johns Hopkins University Press. Baltimore. 2012.
TASKIN, D.;YILDIZ, C.; KANBOLAT, O.; BAKI,A. Reflections of Problem Solving Environment Based on Group Work: Example of Fibonacci Problem. Mediterranean Journal of Educational Research, Canakkale, Turkey, v. 14a, pp. 170-175. 2013.
TAYLOR, J. R. Human Error in Process Plant Design and Operation: A Practitioner’s Guide. CRC Press. Boca Raton, FL. 2016. https://do.org/10.1201/b19075
WELLS, D. Games and mathematics. Subtle connections. Cambridge University Press. New York. 2012. https://doi.org/10.1017/CBO9781139175838
WOODS, D. D. Behind Human Error. Second Edition. Ashgate Publishing Company. UK. 2010.
Appendix
Transcripts of personal and group answers and arguments.

License
Gondola, Ens Aprend Cienc. is an open-access publication, free of charge for authors and readers. The publication, consultation or download of the contents of the magazine does not generate any cost for the authors or the readers, since the Francisco José de Caldas District University assumes the expenses related to edition, management and publication. The peer evaluators do not receive any economic retribution for their valuable contribution. The work of all the actors mentioned above is understood as a contribution to the strengthening and growth of the research community in the field of Science Education.
As of December 1, 2018 the contents of the journal are published under the terms of the Creative Commons License Attribution-Noncommercial- ShareAlike 4.0 International (CC-BY-NC-SA 4.0), under which others may distribute, remix, retouch, and create from the work in a non-commercial way, give credit and license their new creations under the same conditions.
The copyright holders are the authors and the journal Gondola, Ens Aprend Cienc. The holders retain all rights without restrictions, respecting the terms of the license in terms of consultation, downloading and distribution of the material.
When the work or any of its elements is in the public domain according to the applicable law in force, this situation will not be affected by the license.
Likewise, we encourage authors to deposit their contributions in other institutional and thematic repositories, with the certainty that culture and knowledge is a good of all and for all.