DOI:
https://doi.org/10.14483/udistrital.jour.gdla.2017.v12n1.a5Publicado:
2017-01-01Methodological strategy to achieve developing evaluation in mathematics at the Kuando Kubango, Angola teacher training school
Estrategia metodológica para lograr la evaluación desarrolladora de la matemática en la escuela de formación de profesores de Kuando Kubango, Angola
Palabras clave:
evaluation of mathematical knowledge, evaluation of mathematical learning, teacher education (en).Palabras clave:
evaluación de conocimientos matemáticos, evaluación de matemática, formación de profesores (es).Descargas
Referencias
Alfonso Easy, P., Arisyennys Yakelin Easy, P., & Yelena Selpa, M. (2011). Metodología para el estudio de los problemas ambientales en la clase desarrolladora e integradora sobre educación ambiental. Cuadernos de Educación y Desarrollo (28), 23 - 45.
Alfredo Rebollar, M., Maribel Ferrer, V., & Ana Bubaire, Q. (2010). La resolución de sistemas de problemas y ejercicios, un reto a la elevación de la calidad del aprendizaje en la secundaria. Cuadernos de Educación y Desarrollo(15), 12 - 23.
Alina Padrón, V., Lázaro Cruz, R., & Anabel Vizcaino, M. (2011). El proceso de enseñanza-aprendizaje desarrollador desde la clase de español. Cuadernos de Educación y Desarrollo (24), 34 - 45.
Alonso, L. A. P., Sánchez, R. A. P., & Cardozo, A. Z. C. (2016). El razonamiento como eje transversal en la construcción del pensamiento lógico. Praxis & Saber, 7(14), 219-143.
Ballester Pedroso, S. (2002). El transcurso de las líneas directrices en los programas de Matemática y la planificación de la enseñanza. La Habana.
Barred, B. M. B., Noguel, M. F., & Téllez., I. V. (2011). Una aproximación a la utilización de la evaluación educativa para la mejora del proceso pedagógico. Cuadernos de Educación y Desarrollo, 3(25), 56 - 67.
BASTART ORTÍZ, E. A., REYES MEDIACEJA, R., & GONZÁLEZ GILART, G. (2013). Concepción didáctica en la estructuración lógica del sistema de habilidades de la asignatura Pediatría. EDUMECENTRO, 5(1), 55-68.
BLANCO NIETO, L. J., & CÁRDENAS LIZARAZO, J. A. (2014). La Resolución de Problemas como contenido en el Currículo de Matemáticas de Primaria y Secundaria The problem solving as content in the Mathematics Curriculum of Elementary and Secondary education. Revista de Educación Campo Abierto, 32(1), 137-156.
CASTELLANOS, D. (2001). Aprender y enseñar en la escuela. Ciudad de la Habana: Editorial Pueblo y Educación.
CASTELLANOS, D., CASTELLANOS, B., LLIVINA, M., & SILVERIO, M. (2001). Hacia una concepción del aprendizaje desarrollador. La Habana: Universidad Pedagógica “Enrique José Varona.
CASTELLANOS SIMONS, D. (2003). Estrategias para promover el aprendizaje desarrollador en el contexto escolar. La Habana. Universidad Pedagógica Enrique José Varona.
COON, D., & MITTERER, J. O. (2012). Psychology Modules for Active Learning. Brock University: Cengage Learning Customer & Sales Support.
D´ANGELO HERNÁNDEZ, O. (2002). Proyecto de vida y desarrollo integral humano. Revista Internacional Crecemos, 6(2), 34 - 56.
DE GUZMÁN, M. (2007). Y la matemática. Revista iberoamericana de educación(43), 19-58.
de la Cruz Rodríguez, R. D. (2016). Teorías implícitas sobre evaluación en matemáticas que poseen los docentes en formación inicial de las universidades de extremadura españa y trujillo perú. (Máster Oficial Interuniversitario de Investigación en la Enseñanza y el Aprendizaje de las Ciencias Experimentales, Sociales y Matemáticas Especialidad: Didáctica de las Matemáticas), Universidad de Extremadura, Badajoz, España.
DE ROJAS GÓMEZ, M. C., CÁRDENAS, A. L. P., PÉREZ, M. E. H., & PASCUAL, I. G. (2012). Hacia una concepción desarrolladora en la calidad de la evaluación del aprendizaje. Propuesta de Manual. EDUMECENTRO, 4(3), 14-18.
ENCARNACIÓN, C. E. K. E. (2013). Estrategia para favorecer el desarrollo de la interactividad cognitiva en entornos virtuales de enseñanza aprendizaje. Strategy to improve the development of cognitive interactivity in virtual learning environments. Nº 42, 89 - 95.
FALGUERAS, R. P. (2006). Hacia una evaluación desarrolladora en la enseñanza de las ciencias naturales. Ciudad de la Habana: IPLAC.
FALMAGNE, R. J. (2015). Reasoning: Representation and Process: In Children and Adults: Psychology Press.
GAMBOA ARAYA, R. (2014). Relación entre la dimensión afectiva y el aprendizaje de las matemáticas. Revista Electrónica Educare, 18(2), 117-139.
GÓMEZ GÓMEZ, J. C. (2013). Caracterización de las prácticas evaluativas de los docentes de matemática de la institución educativa los palmitos, sucre - colombia. Escenarios, 13, 96 - 107.
HERNÁNDEZ, W. G., SENTÍ, V. E., & LLANTADA, M. M. (2004). Contribución al desarrollo de la creatividad a través de la enseñanza de la programación. Revista pedagogía universitaria, 9, 30-45.
LÁNIZ, C., MARÍA, F., & IVONNE, P. (2013). Estudio de la calidad educativa en el área de matemática, del instituto técnico superior “eugenio espejo” de la ciudad de babahoyo, provincia de los rios. Retrieved from http://repositorio.utb.edu.ec:8080/handle/123456789/1254
LANTOLF, J. P., THORNE, S. L., & POEHNER, M. E. (2015). Sociocultural theory and second language development. Theories in second language acquisition: An introduction, 207-226.
LEONARDO GÁRCIGA, G. (2011). Propuesta de material de estudio para la evaluación del proceso de enseñanza aprendizaje en la asignatura administración. Cuadernos de Educación y Desarrollo (28), 78 - 89.
LÓPEZ FERNÁNDEZ, R., GUTIÉRREZ ESCOBAR, M., VÁZQUEZ CEDEÑO, S., BENET RODRÍGUEZ, M., TEREÑES CASTELLÓN, C., & LEGRÁ NÁPOLES, S. (2012). La evaluación en la educación a distancia en la búsqueda de un aprendizaje desarrollador. Medisur, 10(2), 102-108.
MORENO, E. R. (2013). Creencias y práctica en profesores de ciencias: ideas para pensar un programa de desarrollo profesional desde la evaluación docente. Revista de Estudios y Experiencias en Educación, 11(22), 34 - 56.
MOSQUERA, O. (2011). El reconocimiento del concepto función en estudiantes de la carrera de Ingeniería Industrial. Matanzas. (Tesis en opción al título de Master en Matemática Educativa), Universidad de Matanzas “Camilo Cienfuegos”, Matanzas.
PORTELLES, C. V. S., GONZÁLEZ, M. C. D., & LEYVA, G. M. S. (2013). Hacia un aprendizaje desarrollador en las ciencias biológicas. Cuadernos de Educación y Desarrollo (31), 67 - 80.
QUIALA, C. B. T. (2013). Metodología psicodidáctica para concebir una clase desarrolladora de la personalidad. Formación en investigación, 2(04), 86 - 92.
RAMÍREZ OYARZO, R. R. ( 2013). Estrategia metodológica para el desarrollo de la competencia comunicativa profesional en idioma inglés en la licenciatura en periodismo- Universidad Tecnológica Equinoccial del Ecuador. (Tesis presentada en opción al Grado Científico de Doctor en Ciencias Pedagógicas.), Matanzas.
RICO, L. (1995). Consideraciones sobre el currículo escolar de matemáticas. Revista Ema, 1(1), 4-24.
RICO MONTERO, P. (2002). Técnicas para potenciar en aprendizaje desarrollador en el escolar primario. La Habana: Editorial Pueblo y Educación.
RICO MONTERO, P., PALMA, E. S., & CUERVO, V. M.-V. (2004). Proceso de enseñanza-aprendizaje desarrollador en la escuela primaria. formato electrónico, La Habana.
RODRÍGUEZ, A. R. (2014). La transformación de los dogmas restrictivos sostenidos por los docentes en la dirección del aprendizaje de la matemática de la educación media general politécnica y laboral. Revista Didasc@ lia: Didáctica y Educación. ISSN 2224-2643, 5(2), 1-14.
Cómo citar
APA
ACM
ACS
ABNT
Chicago
Harvard
IEEE
MLA
Turabian
Vancouver
Descargar cita
DOI: 10.14483/udistrital.jour.gdla.2017.v12n1.a5
ESTRATEGIA METODOLÓGICA PARA LOGRAR LA EVALUACIÓNDESARROLLADORA DE LA MATEMÁTICA EN LA ESCUELA DE FORMACIÓN DE PROFESORES DE KUANDO KUBANGO, ANGOLA
Methodological strategy to achieve the developing evaluation of mathematics at the KuandoKubango, Angola teacher training school
Miguel Kanhime Kasavube1
Walfredo González Hernánde2
Para citar como este artículo: Kanhime, M., González-Hernández, W. (2017). Estrategia metodológica para lograr la evaluación desarrolladora de la matemática en la escuela de formación de profesores de Kuando Kubango, Angola. Góndo- la, Enseñ Aprend Cienc, 12(1), 73-91. doi: 10.14483/udistrital.jour.gdla.2017.v12n1.a5.
Recibido: 15 de julio 2016 / Aceptado: 2 de diciembre de 2016
1 Doctor en Ciencias Pedagógicas, Dirección Provincial de Educación. Provincia Kuando Kubango, Angola. Correo electrónico: mkanhime@yahoo.com.br
2 Doctor en Ciencias Pedagógicas. Profesor Titular de Ingeniería Informática. Universidad de Matanzas, Cuba. Correo eletcrónico: walfredogh@gmail.com
R e s u m en
En este artículo se realiza un análisis de los fundamentos teóricos que permiten examinar las características esenciales de la evaluación desarrolladora para la formación de profesores de matemática. En nuestra perspectiva es indispensable el análisis de la evaluación como proceso en el cual se integran los más variados elementos psicológicos, filosóficos, didácticos y matemáticos. Por ende, la definición de esta categoría didáctica es de vital importancia si se pretende su desarrollo en un entorno como el angolano. Para la implementación de la propuesta se utiliza un paradigma predominantemente cualitativo, basada en datos obtenidos de la aplicación de varios métodos empíricos. Se presenta la estrategia para lograr el desarrollo de este tipo de evaluación en el contexto socio-histórico relacionado con la formación del profesional. Por último, se presentan los resultados de la aplicación de la estrategia propuesta.
Palabras claves: evaluación de conocimientos matemáticos, evaluación de matemática, formación de profesores.
Abstract
In this paper we did an analysis of theoretical foundations in order to study essential characteristics of developing evaluation in Mathematics teacher’s education. From our perspective it is essential to analyse evaluation as a process integrating aspects from a variety of disciplines like psychology, philosophy, didactics and mathematics. Thus, is very important to clarify this didactic category designed specially to develop evaluation processes in Angola's context. For development of this proposal a qualitative paradigm is used predominantly, based on data obtained through several empirical methods. We present the strategy to achieve this evaluation process on the socio- historical context, promptly related with professional's training. Finally, we present results of testing this strategy.
Keywords: evaluation of mathematical knowledge, evaluation of mathematical learning, teacher education.
Introducción
Cada día son más los docentes que piensan que la educación requiere cambios profundos, bien planificados que involucren a todos los interesados en el proceso de enseñanza y aprendizaje: profesor, alumno, padres y la sociedad. Cuando se analiza el papel del profesor, la escuela necesita propuestas concretas a sus problemas sobre cómo actuar ante procesos de desmotivación y el desinterés continuados en el estudiante hacia el aprendizaje escolarizado y de los padres hacia los procesos educativos de sus hijos. En realidad, este es un problema de carácter didáctico, metodológico y social. Un elemento detectado en la literatura consultada que influyen en esta situación es el papel de la evaluación del aprendizaje (Coon y Mitterer, 2012; Lantolf, Thorne, y Poehner, 2015; Rico, 1995).
La situación es más compleja cuando realiza un análisis de la asignatura de matemática. Es aquí donde se detectan los mayores índices de estudiantes desaprobados que desertan del sistema educativo (Rodríguez, 2014). Se concuerda con la investigación de Gómez Gómez que plantea:
[…] la llamada ‘cultura de la evaluación’ aún no es una constante […]. Es probable que actualmente los docentes de matemática de algunas escuelas, estén haciendo de la evaluación una práctica evaluativa sin sentido, o discordante, alejados de buscar oportunidades de mejoramiento de los procesos educativos. Aún se observa que se valora el aprendizaje o desempeño de los educandos mediante escalas numéricas, es decir, de tipo cuantitativa en la que no se da cuenta de las implicaciones de evaluar integralmente, como es la tendencia actual en muchas comunidades educativas, la evaluación inicial o diagnóstica y la formativa. (2013, p. 98)
Lo anterior se constata en la asignatura de matemática que se imparte como parte del currículo de los futuros profesores de matemática en escuela media de Menongue, en la provincia de Kuando Kubango. Los autores, desde sus experiencias, identifican que el proceso evaluativo sigue siendo tradicional. El estudiante aún es un ente pasivo en la evaluación de los conocimientos que transmite el profesor, estudia para alcanzar la calificación mínima que les permita promover a otro nivel de enseñanza, afectando así la calidad de su formación. Aun cuando estos resultados se refieren a la preparación de estudiantes como futuros profesores de Menongue, en la literatura consultada (Alonso, Sánchez, y Cardozo, 2016; D´Angelo Hernández, 2002; De Guzmán, 2007; Falmagne, 2015) se refleja como una problemática de la cual no se presenta en diversos países con diferentes niveles de desarrollo. Se puede concluir de lo detectado que la evaluación no está cumpliendo la función informativa y reguladora expresada anteriormente.
Sin embargo, es importante formar a los futuros profesores en una evaluación desarrolladora, ya que según un estudio de la Universidad de Extremadura han detectado que
[…] al momento de evaluar no sabrían cómo hacerlo debido a la gran diversidad de factores que intervienen en el proceso evaluativo lo cual nos conlleva a reflexionar, en primer lugar, a como fuimos evaluados cuando éramos estudiantes de educación básica, de cómo los docentes nos evalúan en la universidad. (de la Cruz Rodríguez, 2016, p. 32)
Cuestión que coincide con lo detectado en la formación de profesores de matemática de Menongue. A partir de la exploración empírica, se pudo revelar en los estudiantes que se preparan como profesores de matemática en la escuela de Menongue, provincia de Kuando Kubango, variadas insuficiencias que constituyen un reflejo de las deficiencias que acompañan la evaluación de contenidos matemáticos, identificando como situación problemática la siguiente:
• Deficiente dominio por la mayoría de los profesores sobre la evaluación. • La evaluación del estudiante es basada en pruebas parciales, sin tener en cuenta la relación entre objetivos, contenidos, métodos y medios de enseñanza. • El profesor utiliza la evaluación como herramienta de control y dominio de los estudiantes. • En la evaluación no se tiene en cuenta las habilidades ni la creatividad en los estudiantes, lo que constituye un freno a su desarrollo integral.
Como parte de los pilares teóricos de la evaluación para que esta desarrolle de manera integral al estudiante se ubican, algunos autores coinciden en señalar que en la enseñanza el maestro juega un papel importante en la conducción del proceso a partir de su actividad como tal (Alfredo Rebollar, Maribel Ferrer, y Ana Bubaire, 2010; Lániz, María, y Ivonne, 2013; Moreno, 2013; Quiala, 2013). Los mismos reconocen el papel rector del maestro en la formación de la personalidad de manera integral a través del aprendizaje. Sin embargo, en estos autores no se detectan resultados científicos encaminados a esclarecer una posible solución a la evaluación desarrolladora de los contenidos matemáticos en la escuela de formación de profesores detectado empíricamente. Ello conduce a la determinación del siguiente problema científico: ¿Cómo contribuir a la evaluación desarrolladora de la matemática durante la formación de profesores de esta área en Menongue?
Solucionar ese problema científico determinó como objeto de estudio la evaluación desarrolladora de contenidos matemáticos y como campo de acción la evaluación desarrolladora de contenidos matemáticos en la formación de profesores de matemática de Menongue, provincia Kuando Kubango.
El objetivo de la investigación es diseñar una estrategia metodológica para contribuir a la evaluación desarrolladora de contenidos matemáticos en la formación de profesores de matemática de Menongue.
Desarrollo
Fundamentos teóricos de la evaluación desarrolladora de los contenidos matemáticos
Diversos autores buscan dar respuesta a los procesos de aprendizaje y desarrollo a partir de la elaboración de variados resultados didácticos que enriquezcan la enseñanza para llegar al objetivo central: el desarrollo integral de la personalidad de los estudiantes. Para ello, es importante que el alumno participe en un proceso de desarrollo al máximo sus potencialidades (Castellanos, 2001; Castellanos, Castellanos, Llivina, y Silverio, 2001).
Para varios autores, el aprendizaje desarrollador es el proceso de apropiación realizado por alumno de los saberes de la humanidad, en constante orientación e interacción social (Alfonso Easy, Arisyennys Yakelin Easy, y Yelena Selpa, 2011; Alina Padrón, Lázaro Cruz, y Anabel Vizcaino, 2011; Portelles, González, y Leyva, 2013; Quiala, 2013; Rico Montero, Palma, y Cuervo, 2004). Para apropiarse de los saberes de la humanidad es prioritario que el proceso sea activo, reflexivo y autoregulado. Al lograr un proceso con estas características, el estudiante logra aprender, de forma gradual, acerca de la realidad, cómo ejecutar diversas acciones, cómo debe actuar ante determinadas situaciones y cómo interactuar con lo demás. Todo ello se logra, por supuesto, en el contexto histórico social en que se encuentra, con un objetivo fundamental: el desarrollo de la personalidad del estudiante.
Otros autores coinciden en afirmar que le corresponde al estudiante asumir un rol preponderante en su proceso de aprendizaje a partir de la construcción y reconstrucción de sus saberes (Bastart Ortíz, Reyes Mediaceja, y González Gilart, 2013; Encarnación, 2013; López Fernández et al., 2012). Este propósito se puede lograr sobre la base del desarrollo de un pensamiento creativo que se materialice en un nuevo estilo de aprendizaje. Sin embargo, para ello es necesario que el proceso cognitivo sea productivo, generalizador y conceptual, construir para sí, además de los conocimientos tradicionales como el mundo externo y objetivo, conocimientos sobre su aprendizaje y su propia personalidad, necesidades, vías y formas de actuar (metaconocimientos), entre otras cuestiones.
Para caracterizar el aprendizaje desarrollador de la matemática, que debe comenzarse por el análisis por la enseñanza de esta ciencia. En la actividad matemática es esencial que se coordinen las acciones de identificación, selección y aplicación de los conocimientos, tanto en ejercicios como en problemas. Estas acciones propician la comunicación, tanto del profesor con sus estudiantes como entre estos y del estudiante consigo mismo, en función de los conocimientos matemáticos, el desarrollo elementos de autovaloración como conocimiento de sí, entre otras, que le permita la regulación de su aprendizaje a partir de la actividad valorativa. En relación con los problemas matemáticos, se aprecia que no está dirigido a potenciar el aprendizaje desarrollador desde su tratamiento más allá de la activación-regulación y en particular del trabajo con la metacognición. La literatura especializada que aborda el control, la reflexión y la autorregulación lo ha hecho fundamentalmente desde la perspectiva de la resolución de problemas, donde son más observables estas manifestaciones en los estudiantes, ofrece más posibilidades para su estudio y resultan ser condiciones necesaria para el que resuelve (Ballester Pedroso, 2002; Blanco Nieto y Cárdenas Lizarazo, 2014; Lániz et al., 2013; Rodríguez, 2014).
Sin embargo, aprender matemática no solo es aprender a resolver problemas sino también aprender a aprender matemática el cual conduzca a un aprendizaje desarrollador de la matemática. Como expresa la autora:
[...] proceso de enseñanza-aprendizaje en las clases de la asignatura Matemática desde un enfoque desarrollador se considera como: el sistema de interacciones que se dan entre los estudiantes, su grupo, el profesor y la tarea escolar, donde el profesor orienta, promueve, estimula y controla el aprendizaje de la Matemática, teniendo en cuenta el desarrollo actual para ampliar continuamente los límites de la zona de desarrollo próximo potencial y favorecer el aprender a aprender Matemática. El estudiante, en interacción y colaboración con los demás estudiantes, participa de forma activa, autorregulada, reflexiva, significativa y motivada, en la apropiación del saber y el poder matemático, de estrategias de aprendizaje cognitivas y metacognitivas, de los procesos de pensamiento y formas de trabajo propias de la matemática, su simbología y terminología, en la formación de sentimientos, actitudes y valores, propiciando su desarrollo integral, a partir de su auto-perfeccionamiento y su autonomía, en estrecha relación con los procesos de socialización, compromiso y responsabilidad social. (Gibert Benítez, 2012, p. 12).
La evaluación desarrolladora de conocimientos matemáticos como componente del proceso de enseñanza aprendizaje
La evaluación es componente indispensable de toda actividad humana y provee a esta de una de sus funciones esenciales: su regulación. Este proceso de regulación puede ser producto de un control externo al propio sujeto o los sujetos de la actividad de se trata, una regulación interna, o de ambas. Para que la evaluación de los conocimientos matemáticos sea desarrolladora es preciso que el proceso sea completamente desarrollador, que integre tanto evaluaciones escritas como orales así como involucrar afectivamente al estudiante (Gamboa Araya, 2014). Para que la evaluación de los conocimientos matemáticos sea desarrolladora es importante movilizar la esfera afectiva del estudiante (Gamboa Araya, 2014). En este artículo se asume que en la evaluación de un aprendizaje desarrollador de la matemática debe primar la función valorativa de este proceso, teniendo en cuenta el aprendizaje de los estudiantes. Lo planteado es importante para orientar y regular la enseñanza con la finalidad de un desarrollo integral de su personalidad, considerando las formas de trabajo y pensamiento de la matemática.
De lo anterior se infiere que la evaluación puede ser de índole personal o grupal. La evaluación es transversal a cualquier proceso de aprendizaje y juega un papel regulador para propiciar la discusión de alternativas y procedimientos. Para lograrlo se debe emplear la crítica y la autocrítica de manera habitual durante la coevaluación y la autoevaluación. Al potenciar estos elementos la evaluación se convierte en un proceso desarrollador para el aprendizaje de los estudiantes. De estas consideraciones se desprende que la coevaluación, autoevaluación, heteroevaluación y metaevaluación deberían transitar desde lo simple hasta lo complejo, de lo particular a lo general e intervenir oportunamente para que el estudiante busque, activamente, cómo resolver lo planteado. La integración de la coevaluación, la autoevaluación, la heteroevaluación y la metaevaluación en un sistema coherente y armónico de evaluación puede contribuir al desarrollo de un aprendizaje desarrollador por las potencialidades que cada una de ellas ofrece.
La consideración de las relaciones que se dan entre los elementos que intervienen en la evaluación del aprendizaje ayuda a comprender mejor la naturaleza interactiva de la evaluación y se pueden identificar los siguientes componentes:
I. El estudiante puede evaluar y ser evaluado. Estos procesos de evaluación y autoevaluación convierten al estudiante en sujeto y objeto de evaluación. Ello implica incrementar la condición de sujeto en su proceso evaluativo como componente de su formación profesional y por las peculiaridades de su desarrollo.
II. El profesor y demás estudiantes como evaluadores. En el nivel universitario es esencial la evaluación de sí y a partir de los otros, sea profesor u otro estudiante. Esta importancia es concedida a partir de su potencialidad en el desarrollo de la personalidad de los estudiantes. Además, permite al profesor cumplir la misión y función social que la educación superior le encomienda.
III. La rama del saber humano que debe ser apropiada por el estudiante, en este caso el enseñar matemática, la cual tiene un reflejo importante en los objetivos y contenidos de enseñanza, así como para su evaluación.
IV. El significado del concepto evaluación del aprendizaje debe ser movida para una ampliación cada vez mayor de su significado hacia un proceso cada vez más orientado al desarrollo personal y no a la satisfacción de encontrar errores en el aprendizaje de los estudiantes.
Para varios autores, todo proceso evaluativo ha de verse en vínculo estrecho con el diagnóstico de cada escolar (Barred, Noguel, y Téllez., 2011; de Rojas Gómez, Cárdenas, Pérez, y Pascual, 2012; Falgueras, 2006; Leonardo Gárciga, 2011; Rico Montero, 2002; Rico Montero et al., 2004).
Los análisis realizados anteriormente evidencian de manera consensuada la necesidad de poseer un amplio conocimiento de la asignatura que imparte. Por lo que los autores consideran que la evaluación desarrolladora de contenidos matemáticos en la formación de profesores se puede definir como componente de la didáctica de la matemática. Este es un proceso comunicativo determinado social e históricamente que tiene como objetivo medir e incluir al educando en el cumplimiento de los objetivos previstos para la enseñanza de esta ciencia como expresión de las necesidades sociales. Para ello, se utilizan los más variados medios interactivos retro alimentadores, durante el curso de un aprendizaje desarrollador para la apropiación del contenido matemático que integre todas sus experiencias de vida para el ejercicio de su profesión como profesores de matemática. De la operacionalización de esta variable se obtuvieron sus dimensiones e indicadores:
Dimensión 1: la evaluación como un proceso comunicativo determinado social e históricamente
Indicadores:
1.1 Integración de las más variadas formas de comunicación en la evaluación de manera efectiva, en función del desarrollo del estudiante como profesor de matemática para un contexto socio histórico determinado.
1.3 Integración del lenguaje coloquial y las formas de expresión de los estudiantes con el lenguaje matemático, de tal manera que este ocupe el lugar que le corresponda en los procesos comunicativos que se establezcan para evaluar su aprendizaje.
1.4 Integración del lenguaje simbólico como parte del lenguaje matemático en su comunicación diaria para la eliminación de las ambigüedades propia de la lengua.
1.5 Utilización de las nuevas tecnologías de la información y las comunicaciones en función del aprendizaje de la matemática (software educativo, internet).
1.6 Relaciones interpersonales buenas que desarrolla en el grupo y con los profesores en su escuela, así como con los estudiantes, docentes y directivos del centro de práctica
1.7 Participación en los diferentes eventos científicos como parte de la socialización y generalización de los resultados que alcanza.
1.8 Vínculo comunicativo que logra con la comunidad y la familia para extender su accionar educativo y socio cultural.
Dimensión 2: valoración del cumplimiento de los objetivos previstos como expresión de las necesidades sociales
Indicadores:
2.1 Derivación gradual de los objetivos hasta el nivel que se aspira evaluar en correspondencia con el modelo del profesor de matemática que se aspira formar.
2.2 Concreción del sistema de objetivos de manera clara y precisa en el instrumento de evaluación.
2.3 Claridad en los criterios y medidas de evaluación, así como las normativas vigentes para su implementación.
2.4 Correspondencia entre las necesidades de evaluación de los estudiantes como profesores de matemática, su práctica social y los objetivos de formación previstos.
2.5 Responsabilidad en su componente práctico a partir su puesta en práctica de los principales componentes organizacionales de la enseñanza de la matemática.
2.6 Motivación para el cumplimiento de sus obligaciones profesionales como profesor de matemática.
2.7 Influencia que logra en los resultados del proceso de enseñanza aprendizaje de la matemática.
2.8 Habilidades y capacidades pedagógicas profesionales para lograr una adecuada integración entre lo académico y lo laboral como profesor de matemática.
2.9 Empleo que logra de las nuevas tecnologías de la información para favorecer el proceso de enseñanza aprendizaje de la matemática, así como de la investigación científica en la enseñanza de la misma.
2.10 Dominio de la metodología de la investigación y la didáctica de la matemática para el nivel que se prepara.
2.11 Rol que desempeña en la dirección del proceso de formación de la personalidad de los estudiantes que atiende.
Dimensión 3: apropiación del contenido matemático que integre todas sus experiencias de vida para la profesión
Indicadores:
3.1 Posee proyección futura como profesional de la enseñanza de la matemática, regulando sus modos de actuación necesarios para el ejercicio de su profesión.
3.2 Desarrolla los procesos metacognitivos orientados a la apropiación del contenido matemático necesario para el ejercicio de su profesión.
3.3 Se apropia del contenido matemático para el ejercicio de su profesión como profesor de matemática con un alto nivel cognitivo.
3.4 Resuelve los problemas de su entorno en los cuales puedan ser aplicados los contenidos de la asignatura matemática o su enseñanza de manera eficiente.
3.5 Motivación por la autosuperación permanente a partir del empleo de la bibliografía complementaria y el uso de las tecnologías de la información en su formación matemática.
3.6 Logro de interpretaciones en el plano cognitivo a partir de los nexos interdisciplinarios de la matemática con otras asignaturas.
3.7 Empleo de la ciencia en la solución de las diferentes problemáticas derivadas de la práctica pedagógica en la matemática.
3.8 Motivación que demuestra para el perfeccionamiento continuo de su formación científica como profesor de matemática.
3.9 Desarrollo de las actividades de carácter independiente relacionadas con su profesión como docente de matemática.
Dimensión 4: la evaluación como proceso individual y colectivo
Indicadores:
4.1 La apropiación de los tipos de evaluación que permita la evaluación de manera integrada durante su formación en el proceso pedagógico de la matemática.
4.2 Reconocimiento de la evaluación como un proceso grupal e individual al mismo tiempo que les permita regular su aprendizaje.
4.3 Reconocimiento de la variedad de opiniones en la evaluación de tal manera que permita desarrollar instrumentos sin ambigüedades, tanto en las preguntas como en las claves para el proceso de calificación grupal.
4.4 Reconocimiento de sus errores como parte del proceso y trazar estrategias para el aprendizaje a partir de ellos, así como del error de los otros.
4.5 Valoración de la influencia que logra en los resultados del proceso de enseñanza y aprendizaje que dirige.
Estrategia metodológica para contribuir a la evaluación desarrolladora de contenidos matemáticos en la formación de profesores de matemática
Varios autores expresan que el empleo de la estrategia data desde la antigüedad, nace en el campo militar y se introduce en el mundo académico por Von Newman en 1944, con la teoría de los juegos (Ceballos Cherigo, 2008; León González, Barcia Martínez, 2012; Ramírez Oyarzo, 2013; Torres Barandela, Gorina Sánchez, Alonso Berenguer, 2013). Etsos autores refieren que se introdujo en la teoría de la dirección desde 1962 y en la pedagogía desde 1987, convirtiéndose en la herramienta de dirección más empleada en el mundo.
Las estrategias, en el marco del proceso enseñanza aprendizaje, han sido abordadas desde distintos puntos de vista. Como se evidencia en las opiniones de los autores, no existen estrategias universales para los problemas, sino que cada situación requiere de un tratamiento diferente. De la Torre refiere que, en el ámbito educativo, el término estrategia se viene utilizando con el significado de método o combinación de métodos, procedimientos y principios (2002, p. 105). El principal componente, dice, es la planificación, se refiere a la construcción de una posición teórica-metodológica que implique un proceso de enseñanza-aprendizaje, apoyado en leyes, principios y categorías como: instrucción, educación y desarrollo del sujeto.
Es parte de un diagnóstico integral y considera la importancia de la actividad, la comunicación, la socialización y la unidad de lo cognitivo, lo volitivo y lo afectivo para cumplir una meta. Para Castellanos Simons, la estrategia es una “[…] guía consciente intencional que proporciona una regulación general de la actividad y da sentido y coordinación a todo lo que hacemos para llegar a una meta o fin, teniendo en cuenta las características de cada contexto y las circunstancias concretas” (2003, p. 107). Como se deriva de esta definición, las estrategias se componen de acciones flexibles y adaptativas para la solución de problemáticas cuyo surgimiento se encuentra en el proceso enseñanza-aprendizaje y su inicio se encuentra en las variables definidas al investigar el proceso en el cual pretenden incidir y se trata de modificar.
Como definición de estrategia metodológica se encuentra la asumida por Ramírez Oyarzo quien, a su vez, destaca el vínculo entre el aspecto cognoscitivo y el afectivo, que debe presidir todo proceso de transformación dirigido por una estrategia, al señalar que:
La estrategia se diseña a partir de acciones que propicien un ambiente favorable, y parte de diagnosticar el nivel de conocimientos que posee el colectivo pedagógico, sus habilidades, su actuación; pero también de sus intereses, sus motivaciones y necesidades para enfrentar un cambio cualitativo en los estudiantes […]. (Ramírez Oyarzo, 2013, p. 63)
Lo cual concuerda con la estructura y objetivo de la estrategia que se propondrá en este artículo. La estrategia metodológica propuesta que se observa en la figura 1 contribuirá al perfeccionamiento y enriquecimiento de la construcción teórico-metodológica de la asignatura matemática. Una vez se dé su aplicación en el contexto del proceso pedagógico, crea nuevas posibilidades de planificar, orientar, dirigir, controlar y evaluar el proceso de enseñanza aprendizaje, en la enseñanza media. La estrategia metodológica elaborada, en su estructura comprende un conjunto de componentes que en una concepción de sistema contribuyen a la evaluación desarrolladora de contenidos matemáticos. La estrategia metodológica diseñada por los autores tiene, además de los fundamentos ya expresados, los componentes siguientes:
Etapas de la estrategia
Primera etapa: diagnóstico y planificación
En esta etapa se crean las condiciones de información diagnóstica y planificación de las acciones posteriores para el desarrollo de la evaluacióndesarrolladora de contenidos matemáticos en la escuela de formación de profesores de Menongue, provincia Kuando Kubango.
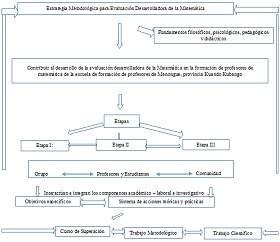
Figura 1. Representación esquemática de la estrategia metodológica que se propone como resultado de la presente investigación.
Fuente: elaboración propia.
Objetivo específico de la etapa
Las acciones que se prevén en la primera etapa, están dirigidas a:
• Identificar la situación de la evaluación desarrolladora de los contenidos matemáticos en la formación de profesores de matemática de la escuela de formación de profesores de Menongue.
• Coordinar las acciones de superación, trabajo metodológico y trabajo científico metodológico que favorezcan el desarrollo de la evaluación desarrolladora de los contenidos matemáticos en la formación de profesores de matemática.
Acciones que se proponen desarrollar
• Diagnosticar el conocimiento acerca de los objetivos de la carrera, así como su perfil y el modelo de profesional que se pretende formar.
• Revisión del proceso evaluativo en las diferentes asignaturas que componen su plan de estudio tanto de formación matemática como pedagógica.
• Diagnosticar el nivel de los conocimientos matemáticos de los profesores que imparten esos contenidos.
• Determinación de las vías que serán utilizadas por el profesor para el diagnóstico del desarrollo de los estudiantes y grupos escolares.
• Diagnosticar los conocimientos sobre la evaluación de conocimientos.
• Diagnosticar el nivel de habilidades para interactuar con los espacios virtuales de enseñanza aprendizaje (Evea).
• Diagnosticar el nivel de formación matemática que poseen los estudiantes.
• Diagnosticar la existencia de vínculos afectivos positivos relacionados con la matemática.
• Diagnosticar el conocimiento que poseen los estudiantes sobre su formación como profesores de matemática.
• Diagnosticar el desarrollo de habilidades informáticas.
Segunda etapa: ejecución de acciones transformadoras con profesores y estudiantes
Objetivo específico de la etapa
• Estructurar el sistema de acciones para la superación de los profesores que se reviertan en una mejor dirección del proceso de evaluación desarrollador en los estudiantes.
Los objetivos fundamentales para la superación de los profesores:
• Analizar los resultados del diagnóstico realizado para estructurar una propuesta de solución para la superación de los profesores.
• Diseñar el sistema de cursos de superación para erradicar las deficiencias detectadas en el diagnóstico.
• Superar a los profesores en los objetivos para el proceso formativo del profesional de la educación en la especialidad de matemática.
• Superar a los profesores en la realización de diagnósticos para ser llevados a cabo desde sus asignaturas que permitan determinar las necesidades formativas de sus estudiantes.
En relación con estos objetivos, se estructuran las acciones correspondientes a la superación de los profesores en la figura 2:
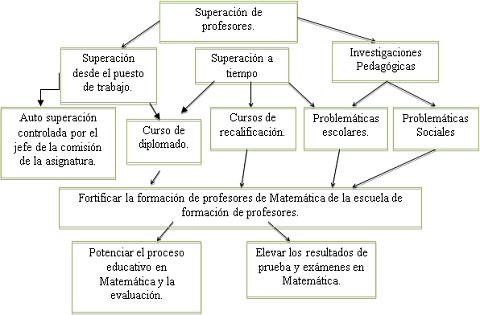
Figura 2. Acciones de superación a profesores.
Fuente: elaboración propia.
Acciones: instalación la herramienta que sustenta el espacio virtual de enseñanza aprendizaje (Evea)
• Implantar los Evea y mostrar sus funcionalidades principales para la creación de cursos.
• Orientar el trabajo con el sitio web.
• Interactuar con el sitio web a través de sus fun- cionalidades principales para la apropiación del sistema de los contenidos de matemática.
• Evaluar la efectividad del sitio en el aprendizaje de los estudiantes.
Acciones encaminadas a los estudiantes
Objetivo: diseñar el sistema de acciones a realizar con los estudiantes que contribuya a la
evaluación desarrolladora de los contenidos matemáticos.
Acciones integradoras:
• El coordinador de la asignatura deberá intercambiar con el representante de la comunidad para que facilite los espacios de búsqueda de problemas a los estudiantes para solucionarlos teniendo en cuenta el perfil profesional del estudiante.
• Orientar a los estudiantes en la resolución de problemas de la vida y de la comunidad, vinculados con el modelo del profesional. Para la introducción de los conocimientos se propone un enfoque problémico de los conocimientos demostrada en la literatura consultada su factibilidad (Hernández, Sentí, y Llantada, 2004, p. 107; Mosquera, 2011)y, para mejorar su fijación, estructurarse de dos formas fundamentales:
• A partir del conocimiento estudiado buscar aplicaciones en la realidad que puedan constituir problemas.
• A partir de los modelos obtenidos en la clase elaborar dos problemas diferentes a los tratados en clase.
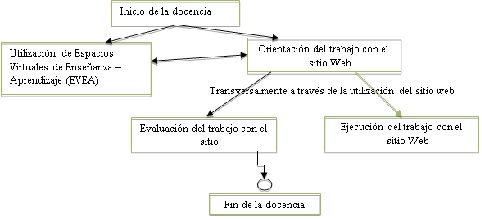
Figura 3.a 3. Acciones para la utilización del sitio web en la enseñanza de la matemática.
Acciones para el desarrollo del trabajo investigativo
Fuente: elaboración propia.
El trabajo investigativo desde los primeros años en la formación de profesores contribuye al desarrollo de habilidades investigativas para el ejercicio de su profesión.
• Participar en investigación de enseñanza de la matemática para que los estudiantes desarrollensus conocimientos matemáticos.
• Aplicar investigación en la escuela donde realizan la práctica para que puedan desarrollar y consolidar conocimientos para aplicar en el futuro, como profesor de matemática en la enseñanza primaria y secundaria básica.
• Fomentar el interés por la matemática en su escuela para desarrollar habilidades en su aprendizaje.
• Crear círculos de interés dirigidos a la resolución de problemas de matemática vinculados con la vida y la comunidad.
Acciones por año
Primero y segundo año.
• Observar y describir la realidad teniendo en cuenta sus problemas matemáticos y su enseñanza.
• Fundamentar sus criterios a partir de la explicación de la realidad realizando análisis de los datos.
• Elaborar conclusiones sobre la base de situaciones específicas de la práctica relacionadas con la matemática y su enseñanza.
Tercer año:
• Comparar la teoría y la práctica en la comunidad o en las escuelas donde se encuentren laborando que les permita identificar las contradicciones.
• Proponer soluciones a los problemas investigados a partir de los conocimientos matemáticos y pedagógicos que poseen.
• Redactar informes de investigación sencillos, donde den cuenta de la solución que han encontrado a las problemáticas relacionadas con el contexto comunitario y escolar. En estos se deben expresar sus resultados más relevantes y demuestren la utilización de métodos de investigación.
Cuarto año:
• Redactar trabajos investigativos y llegar a conclusiones con mayor amplitud y profundidad de criterios que los abordados en años anteriores.
Tercera etapa: control y evaluación de los resultados de las acciones anteriores
Este proceso se inicia desde la primera etapa y se mantiene en todo momento, lo que conlleva a la retroalimentación sucesiva de la misma por parte de los actores que participan. Se realiza la evaluación del nivel de satisfacción de las necesidades básicas diagnosticadas.
Objetivo específico de la etapa
Evaluación de la efectividad de las acciones ya implantadas. Teniendo en cuenta los resultados que se van logrando, de acuerdo con los controles realizados, se evalúa el cumplimiento de lo programado, propuesto en la estrategia metodológica, ofreciendo las sugerencias y recomendaciones para posibles cambios o ajustes en las propuestas.
Acciones que se proponen desarrollar
• Elaborar evaluaciones que abarcan las formas sistemáticas, parciales y finales, enfatizando en la lógica interrelación que debe tener lugar entre estas y considerando los diferentes niveles de desarrollo de la personalidad de los estudiantes.
• Observar clases en el centro de formación de profesores con el objetivo de constatar el desarrollo de una evaluación desarrolladora en los estudiantes y en la práctica para verificar cómo se revierte en su entorno.
• Entrevistar a los representantes de la comunidad para evaluar el impacto social de la práctica de los estudiantes de la escuela de formación de profesores durante la estancia allí.
• Encuestar a los profesores del centro de prácticas de los estudiantes de la escuela de formación de profesores para determinar el nivel de desarrollo de sus estudiantes y las características de las evaluaciones propuestas por ellos.
• Encuestar a los estudiantes del centro de prácticas para determinar el nivel de satisfacción de sus estudiantes con la enseñanza de la matemática y su evaluación.
• Entrevistar a directivos del centro escolar acerca del nivel de desarrollo, así como la formación de los estudiantes de la escuela de formación de profesores para determinar el grado de satisfacción de los directivos con su actuación en el centro escolar.
• Realizar talleres conjuntos periódicos entre los profesores de la escuela de formación y los estudiantes de dicha escuela para corregir las acciones no deseables que puedan ejecutar.
• Visitar periódicamente las actividades desarrolladas por los estudiantes de la escuela de formación de profesores en compañía de los profesores de la escuela de prácticas, de manera que sirva de entrenamiento a ambos las acciones a corregir. En caso de realizarlas en la comunidad con un representante del Soba para el mismo fin.
• Integrar a los directivos de la escuela de prácticas y los representantes de la comunidad a las acciones de autoevaluación y coevaluación a ejecutarse con los estudiantes de tal manera que puedan familiarizarse con estas técnicas.
Diseño de la implementación en la práctica de la estrategia metodológica
Materiales y métodos empleados
El análisis de la validez de la estrategia propuesta consta de tres momentos, como se expondrá a continuación. Posteriormente a elaborar la estrategia, se realizó una consulta a los expertos que permitió valorar la validez de la estrategia a partir de su experiencia en la formación de profesores en el contexto angolano. Los expertos votaron por cada uno de los componentes de la estrategia. Se aplicaron los estadígrafos varianza, desviación típica y variación a la votación de los expertos y sus resultados en la tabla 1 permitieron asegurar si existe o no concordancia entre los criterios de los expertos. Los resultados obtenidos con la aplicación de la estrategia son analizados para determinar, como último paso, la eficacia de la estrategia propuesta. Del criterio de expertos se ejecutaron las acciones recomendadas en la bibliografía obteniéndose los resultados reflejados en la tabla 1:
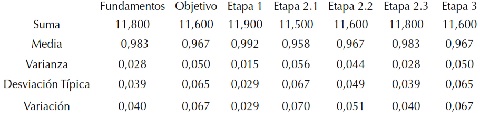
Tabla 1.a 3. Acciones para la utilización del sitio web en la enseñanza de la matemática.
Fuente: elaboración propia.
Se establece la proporción mínima de Vj≤ 0,10 observándose poca variación entre los expertos en la votación para cada atributo.
Aplicación de la estrategia metodológica en el ISCED de Kuando Kubango
Se realiza un preexperimento, en el cual se selecciona un grupo de tercer año, este se sugiere por ser los estudiantes del penúltimo año quienes pueden integrar en mayor medida todos los elementos propuestos de la estrategia. En cada caso, se realiza una validación parcial de la estrategia pues solamente se introducirán las acciones posibles de implementar (ya que está concebida para todos los años de formación). Se realiza un diagnóstico de los estudiantes en el grupo, dos cortes y un diagnóstico final que se presentan en la tabla 2, ocho observaciones a clases que se presentan en la tabla 3 y cinco observaciones a clases que se presentan en la tabla 4 aplicados en el grupo de tercer año.
Se realiza un preexperimento, en el cual se selecciona un grupo de tercer año, este se sugiere por ser los estudiantes del penúltimo año quienes pueden integrar en mayor medida todos los elementos propuestos de la estrategia. En cada caso, se realiza una validación parcial de la estrategia pues solamente se introducirán las acciones posibles de implementar (ya que está concebida para todos los años de formación). Se realiza un diagnóstico de los estudiantes en el grupo, dos cortes y un diagnóstico final que se presentan en la tabla 2, ocho observaciones a clases que se presentan en la tabla 3 y cinco observaciones a clases que se presentan en la tabla 4 aplicados en el grupo de tercer año.
Cada una de las tablas expresan en las columnas el indicador como están numerados en la sección La evaluación desarrolladora de conocimientos matemáticos como componente del proceso de enseñanza- aprendizaje, que fue posible medir dadas las características del método empleado. En el caso de los números contenidos en cada celda indica la cantidad de estudiantes en los cuales se obtuvo un desempeño favorable de los indicadores por para cada medición realizada. Estas mediciones de los indicadores en cada dimensión de la variable dependiente expresadas en el ítem La evaluación desarrolladora de conocimientos matemáticos como componente del proceso de enseñanza aprendizaje,el cual permitió conocer el estado favorable de la variable dependiente y arribar a conclusiones relacionadas con la validez de la estrategia.
De las observaciones a clases se ponen solamente las observaciones iniciales y finales, de tal manera que se aprecie variabilidad en la cantidad de estudiantes que poseen los indicadores estudiados en la observación a clases que impartieron durante su práctica laboral. Como se muestra en la tabla 3:
A continuación, se muestran los resultados de las cinco observaciones a los estudiantes mientras recibían clases en el ISCED de Menongue:

Tabla 2. Número de estudiantes a los cuales se les midieron nueve indicadores en las etapas de diagnóstico, cortes y diagnóstico final.
Fuente: elaboración propia.
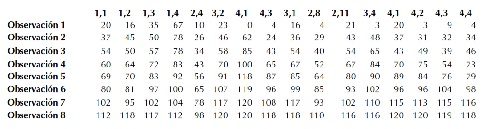
Tabla 3. Resultados de las observaciones a clases de los estudiantes en la práctica laboral.
Fuente: elaboración propia.
Referências
ARAUJO, R. M. L. Práticas Pedagógicas e Ensino Integrado. Versão preliminar para discussão. Belém: Brasil, 2013.
BEANE, J. A. Integração Curricular: A concepção do Núcleo da Educação Democrática. 1ed. Didáctica editora. Lisboa: Portugal, 1997.
______. Integração Curricular: a essência de uma escola democrática. Revista Currículo Sem Fronteiras. v.3, n.2, p.91-110, Jul/Dez 2003.
BRASIL. Lei nº 11.892 de 29 de dezembro de 2008. Institui a Rede Federal de Educação Profissional, Científica e Tecnológica, cria os Institutos Federais de Educação, Ciência e Tecnologia. Brasília, 2008.
BRASIL, Conselho Nacional de Educação (CNE).Resolução nº 2, de 30 de janeiro de 2012 . Define Diretrizes Curriculares Nacionais para o Ensino Médio. Brasília, 2012.
______. Resolução nº 6 de 20 de setembro de 2012. Define Diretrizes Curriculares Nacionais para a Educação Profissional Técnica de Nível Médio. Brasília, 2012.
BRASIL. Ministério da Educação Lei no 9.394, de 20 de dezembro de 1996. Institui as Diretrizes e Bases da Educação Nacional. Brasília, 1996.
______. Decreto nº 5.154, de 23 de julho de 2004. Regulamenta o § 2º do art. 36 e os arts. 39 a 41 da Lei nº 9.394, de 20 de dezembro de 1996, que estabelece as diretrizes e bases da Educação Nacional. Brasília, 2004.
______. Parecer nº 15, de 1º de junho 1998. Estabelece as Diretrizes Curriculares Nacionais para o Ensino Médio. Brasília, 1998.
CIAVATTA, M. A Formação Integrada: a escola e o trabalho como lugares de memória e de identidade. In: FRIGOTTO, G.; CIAVATTA, M; RAMOS, M. (Org.). Ensino Médio Integrado: concepções e contradições. Ed. Cortez. São Paulo: Brasil, 2005.
FAZENDA, Ivani. Integração ou Interdisciplinaridade no Ensino Brasileiro. Efetividade ou Ideologia. Ed. Loyola, 6ed. São Paulo: Brasil, 2011.
FLORES, M.A. O professor: Agente de Inovação Curricular. Mestrado em Educação Universidade do Minho. Braga: Portugal, 1997.
FRANCO, M.C. A Formação Integrada: a escola e o trabalho como lugares de memória e de identidade. In: FRIGOTTO, G.; CIAVATTA, M.; RAMOS, M. Ensino Médio Integrado: concepções e contradições. Ed. Cortez. São Paulo: Brasil, 2005.
FRIGOTTO, G.; CIAVATTA, M. (orgs). Teoria e Educação no Labirinto do Capital. Ed. Vozes, 2ed. Rio de Janeiro: Brasil, 2001.
GATTI, B.A. Grupo focal na pesquisa em ciências sociais e humanas. Ed. Líber Livro. Brasília: Brasil, 2005.
GIL, A.C. Métodos e Técnicas de Pesquisa Social. Ed. Atlas, 5ed. São Paulo: Brasil, 1999.
IFMT. PDI. Cuiabá: Brasil, 2014-2018.
LIBÂNEO, J.C. Adeus professor, Adeus professora? Novas exigências educacionais e profissão docente. Ed. Cortez, 11ed. São Paulo: Brasil,2009.
LOPES, A.C. Os Parâmetros Curriculares Nacionais para o Ensino Médio e a Submissão ao Mundo Produtivo: o caso do conceito de contextualização. Revista Educação e Sociedade. v.23, n.80, p. 386-400. Campinas: setembro/2002.
_____. Interpretando e Produzindo Políticas Curriculares Para o Ensino Médio In: FRIGOTTO, Gaudêncio; CIAVATTA, Maria. Ensino Médio: ciência, cultura e trabalho. Brasília: Brasil, 2004.
LÜDKE, M.; ANDRE, M.E.D.A. Pesquisa em Educação: abordagens qualitativas. Ed. EPU. São Paulo: Brasil 1996.
MARTINS, H.H.T.S. Metodologia qualitativa da pesquisa. Revista Educação e Pesquisa. V.30, n.2, p.289-300. São Paulo: maio/ago. 2004.
MORAES, R.; GALIAZZI, M.C. Análise Textual Discursiva. Ed. Unijuí, 2ed. Ijuí: Brasil,2013.
MORIN, E. Os sete saberes necessários à educação do futuro. Ed. Cortez, 10º ed. São Paulo: Brasil, 2005.
PAVIANI, Jayme. Interdisciplinaridade: conceito e distinções. Educs, 3ed. rev. Caxias do Sul: Brasil, 2014.
PIMENTA, S.G.; GHEDIN, E. (orgs). Professor Reflexivo no Brasil. Gênese e crítica de um conceito. Ed. Cortez, 7ed. São Paulo: Brasil, 2012.
RAMOS. M. Possibilidades e Desafios na Organização do Currículo Integrado In: FRIGOTTO, G.; CIAVATTA, M.; RAMOS, M. (orgs). Ensino Médio Integrado: Concepções e Contradições. Ed Cortez. São Paulo: Brasil, 2005.
______. A Pedagogia das Competências: autonomia ou adaptação? Ed. Cortez, 3ed. São Paulo: Brasil, 2006.
RAMOS MEDEIROS R.C. e CAVALCANTI VALENTE G.S. A Prática Docente Reflexiva baseada no Currículo Integrado: uma questão de competências. Revista Iberoamericana de Educación. V. 54 n.º 2. OEI – 2010.
RODRIGUES, D.S. e ARAUJO R.M.L. Filosofia da Práxis e Ensino Integrado: para além da questão curricular. Revista Trabalho & Educação. V. 20, n.° 1, pp.11-22, Belo Horizonte: jan./abr.2011.
RICHARDSON, R.J. Pesquisa Social: métodos e técnicas. Ed. Atlas. São Paulo: Brasil, 1999.
SACRISTÁN, J.G. O currículo: uma reflexão sobre a prática. Ed. Artmed, 3ed. Porto Alegre: Brasil, 2000.
YIN, Robert. Estudo de Caso: Planejamento e Método. Ed. Bookman. Porto Alegre: Brasil, 2005.
Licencia
Góndola, Ens Aprend Cienc. es una publicación de acceso abierto, sin cargos económicos para autores ni lectores. La publicación, consulta o descarga de los contenidos de la revista no genera costo alguno para los autores ni los lectores, toda vez que la Universidad Distrital Francisco José de Caldas asume los gastos relacionados con edición, gestión y publicación. Los pares evaluadores no reciben retribución económica alguna por su valiosa contribución. Se entiende el trabajo de todos los actores mencionados anteriormente como un aporte al fortalecimiento y crecimiento de la comunidad investigadora en el campo de la Enseñanza de las Ciencias.
A partir del 01 de diciembre de 2018 los contenidos de la revista se publican bajo los términos de la Licencia Creative Commons Atribución–No comercial–Compartir igual 4.0 Internacional (CC-BY-NC-SA 4.0), bajo la cual otros podrán distribuir, remezclar, retocar, y crear a partir de la obra de modo no comercial, siempre y cuando den crédito y licencien sus nuevas creaciones bajo las mismas condiciones.
Los titulares de los derechos de autor son los autores y la revista Góndola, Ens Aprend Cienc. Los titulares conservan todos los derechos sin restricciones, respetando los términos de la licencia en cuanto a la consulta, descarga y distribución del material.
Cuando la obra o alguno de sus elementos se halle en el dominio público según la ley vigente aplicable, esta situación no quedará afectada por la licencia.
Asimismo, incentivamos a los autores a depositar sus contribuciones en otros repositorios institucionales y temáticos, con la certeza de que la cultura y el conocimiento es un bien de todos y para todos.





















