DOI:
https://doi.org/10.14483/23464712.12326Publicado:
2018-01-01A engenharia didática para o ensino de olimpíadas de matemática: situações olímpicas com o amparo do software geogebra
The Didactic Engineering for the Math Olympics Teaching: Olympic Situations with Geogebra’s Support
La ingeniería didáctica para la enseñanza de olimpiadas de matemáticas: situaciones olímpicas basadas en el software Geogebra
Palabras clave:
didactic engineering, GeoGebra, mathematical Olympiads, theory of situations (en).Palabras clave:
geoGebra, ingeniería didáctica, olimpiadas de matemáticas, teoría de las situaciones (es).Palabras clave:
engenharia didática, Geogebra, olimpíadas de Matemática, teoria das situações (pt).Referencias
ALIEVI, P. T. Soluções não clássicas para problemas da OBMEP. 47p. Dissertação (Mestrado Profissional em Matemática – PROFMAT). Universidade Federal de Santa Maria, Rio Grande do Sul, 2013.
ALMOULOUD, S.A. Fundamentos da Didática da Matemática. Editora UFPR. São Paulo: Brasil. 2007.
ALVES, W.J.S. O Impacto da Olimpíada de Matemática em Alunos da Escola Pública.30p. Dissertação (Mestrado Profissional em Ensino de Matemática - PROFMAT). Pontifícia Universidade Católica de São Paulo – PUC, São Paulo, 2010.
ALVES, F.R.V. Insight: descrição e possibilidades de seu uso no ensino do cálculo. VIDYA, Santa Maria, v. 32, n. 2, pp. 149-161, jul./dez. 2012.
ALVES, F.R.V. Engenharia Didática para a generalização da sequência de Fibonacci: uma experiência num curso de licenciatura. Educ. Matem. Pesq., São Paulo, v. 18, n. 1, pp. 61- 93. 2016a.
ALVES, F.R.V. Didática de matemática: seus pressupostos de ordem epistemológica, metodológica e cognitiva. Interfaces da Educação, v.7, n.21, p. 131-150, Paranaíba: Brasil. 2016b.
ARAÚJO, R.R. Perfil de desempenho dos alunos de ensino médio da unidade integrada Henrique Rocha, Tutóia-MA, frente a primeira fase da OBMEP. 45p. Dissertação (Mestrado Profissional em Matemática – PROFMAT), Universidade Federal do Piauí (UFPI), 2015.
ARTIGUE, M. Ingénièrie didactique. In: Brun, J. Didactiques des Mathématiques. Paris: Délachaux et Niestle, 1995a. pp. 243-263.
ARTIGUE, M. Ingenieria Didática. In: Artigue, Michelle; Douady, Régine; Moreno, Luis; Gomez, Pedro. Ingeniéria didatica en Educacion Matemática. Grupo Editorial Iberoamericano, Bogotá: Colombia. pp. 33-61, 1995b. Disponível em: http://funes.uniandes.edu.co/676/1/ Artigue1995Ingenieria.pdf. Acessado em: 20/02/2017.
ARTIGUE, M. Ingénierie Didactique. Recherches en Didactique des Mathématiques. Grenoble: La Pensée Sauvage-Éditions, v. 9.3, p. 281-308, 1998.
BADARÓ, R.L. Do zero às medalhas: orientações aos professores de cursos preparatórios para olimpíadas de matemática. 144p. Dissertação (Mestrado Profissional em Matemática - PROFMAT). Universidade federal da Bahia, Salvador, 2015.
BONFIM, A.P. Produção e Aplicação de Material Didático para estudantes iniciantes em Olimpíadas de Matemática. 243p. Dissertação (Mestrado Profissional em Matemática – PROFMAT). Universidade Federal do Pará, Belém, 2013.
BRAGANÇA, B. Olimpíada de Matemática para a Matemática avançar. 107p. Dissertação (Mestrado Profissional em Matemática - PROFMAT). Universidade Federal de Viçosa, Minas gerais, 2013.
BROUSSEAU, G. Les obstacles épistémologiques, problèmes et ingénierie didactique. In: Théorie des situations didactiques. Grenoble La Pensée Sauvage. Grenoble: Francia. 1998. pp. 115-160.
BROUSSEAU, G. Théorisation des phénomènes d'enseignement des mathématiques. Mathematics. Université Sciences et Technologies - Bordeaux I, 1986.
BROUSSEAU, G. Introdução ao Estudo das Situações Didáticas. 128p. Editora Ática. São Paulo, Brasil, 2008.
CALAZANS, M.V.F. Proposta de implantação do centro preparatório para olimpíadas de matemática. 40p. Dissertação (Mestrado Profissional em Matemática – PROFMAT). Universidade Estadual de Santa Cruz, Ilhéus, Bahia, 2014.
CARVALHO, Márcio M. de. Resolução de problemas matemáticos olímpicos: uma abordagem aritmética modular. 62p. Dissertação (Mestrado Profissional em Matemática – PROFMAT). Universidade Federal do Vale do São Francisco, Bahia, 2013.
CARVALHO, Valessa, Z.F.S. Funções convexas com aplicações em problemas de olimpíadas de matemática. 60p. Dissertação (Mestrado Profissional em Matemática - PROFMAT). Universidade Federal do Piauí, Teresina, 2013.
CARVALHO JÚNIOR, A.L.L. de. Material Multimí- dia: Resolução comentada de algumas questões do nível 3 da OBMEP sobre geometria. 64p.. Dissertação (Mestrado Profissional em Matemática – PROFMAT). Universidade Federal do Pará, Belém, 2013.
COCCO, E.M. Olimpíada de Matemática das Escolas Públicas e avaliação em larga escala: possíveis interlocuções. 161p.. Dissertação (Mestrado em Educação). Universidade Regional Integrada do Alto Uruguai e das Missões, Rio Grande do Sul, 2013.
DOCARMO NETO, V. Teorema de Pitágoras e áreas: sua aplicabilidade no banco de questões da OBMEP. 44p. Dissertação (Mestrado Profissional em Matemática – PROFMAT). Centro de Ciências da Natureza, UFPI, Teresina, 2014.
DOLCE, O.; POMPEO, J.N. Fundamentos de Matemática Elementar. Vol. 9: Geometria Plana. 456p. v. 7. Atual Editora. São Paulo: Brasil. 2008.
FOMIM, D.; GENKIN, S.; ITENBERG, I. Mathematical Circles – Russian Experience. 271p. Mathematical World. v. 7. Estados Unidos da América, 1993.
IEZZI, G.; MURAKAMI, C. Fundamentos de Matemá- tica Elementar. Vol.1 Conjuntos e Função. 317p. 3.ed. Atual Editora. São Paulo: Brasil. 1977.
IGLIORI, S.B.C. A noção de Obstáculo Epistemológico e a Educação Matemática. In Educação Matemática Uma Introdução. Org. Silvia Machado. EDUC. São Paulo. 1999.
JACON, L.S.C; KALHIL, J.B. O professor formador e as competências em tecnologia de informação e comunicação: um estudo sobre quais recursos computacionais estes profissionais utilizam na elaboração do seu material didático. AMAZÔNIA - Revista de Educação em Ciências e Matemá- ticas, v. 8, n. 15 - jul. 2011/dez. p.27-44. 2011.
LACERDA, C.W.P. de. Sequências e séries: conhecendo e construindo estratégias de abordagem. Dissertação (Mestrado Profissional em Matemá- tica – PROFMAT). Universidade Federal Rural de Pernambuco. 2014.
LAGUERRE, E. Une ingenierie didactique pour làppentisssage du theo-reme de Thales au college. Education. Universit_e Paris-Diderot - Paris VII, Français. 2005.
LITVINENKO, V.; MORDKEVICA, A. Solving Problems in Algebra and Trigonometry. Mir Publishers. Moscow: Russia. 1987.
LIDSKI, V.; OVSIANIKOV, L.V.; TULAIKOV, A.N.; SHABUNIN, M. I. Problemas de Matematicas Elementales. 3a. ed. Editorial Mir. Moscu: Russia. 1978.
LORENZATO, S. Por que não ensinar Geometria? A educação matemática em revista. Geometria. Blumenau, n. 04, pp. 03-13, 1995. Disponível em: . Acesso em 11 de janeiro 2017.
MARTINS, R.A. Colinearidade e concorrência em olimpíadas internacionais de matemática: uma reflexão voltada para o ensino da geometria. 2015. Dissertação (Mestrado Profissional em Matemática – PROFMAT). Universidade Federal de Brasília.
NETO, A.C.M. Geometria Plana. Tópicos de matemática elementar, vol.2. Coleção professor de matemática, SBM. 2013.
OLIVEIRA, C.C. do N. Olimpíadas de Matemática: concepção e descrição de “situações olímpicas” com o recurso do software Geogebra. 136 p. Dissertação (Mestrado em Ensino de Ciências e Matemática) - Centro de Ciências, Universidade Federal do Ceará, Fortaleza, 2016.
OLIVEIRA, E.C. de; CHIUMMO, A. Análise da aprendizagem de semelhança de triângulos por alunos de graduação em Matemática. VIDYA, Santa Maria, v. 35, n. 2, p. 179-195, jul./dez., 2015.
Cómo citar
APA
ACM
ACS
ABNT
Chicago
Harvard
IEEE
MLA
Turabian
Vancouver
Descargar cita
DOI: http://doi.org/10.14483/23464712.11732
A ENGENHARIA DIDÁTICA PARA O ENSINO DE OLIMPÍADAS DE MATEMÁTICA: SITUAÇÕES OLÍMPICAS COM O AMPARO DO SOFTWARE GEOGEBRA
THE DIDACTIC ENGINEERING FOR THE MATH OLYMPICS TEACHING: OLYMPIC SITUATIONS WITH GEOGEBRA’S SUPPORT
LA INGENIERÍA DIDÁCTICA PARA LA ENSEÑANZA DE OLIMPIADAS DE MATEMÁTICAS: SITUACIONES OLÍMPICAS BASADAS EN EL SOFTWARE GEOGEBRA
Ana Paula Rodrigues Alves Santos *, Francisco Régis Vieira Alves **
Cómo citar este artículo: Rodrigues Alves Santos, A. P., Régis Viera Alves, F. (2018). A engenharia didática para o ensino de olimpíadas de matemática: situações olímpicas com o amparo do software geogebra. Góndola, Enseñ Aprend Cienc, 13(1), 141-154. doi: http://doi.org/10.14483/23464712.11732.
Recibido: 21 de junio de 2017; aprobado: 28 de noviembre de 2017.
* Possui licenciatura em Matemática pela Universidade Federal do Ceará (UFC) e mestrado em Ensino de Matemática pela Faculdade de Ciências da Universidade do Porto (Portugal). Mestranda do programa de pós-graduação em ensino de ciências e matemática pelo Instituto Federal do Ceará (IFCE). Professora de matemática com ênfase na preparação de alunos para as olimpíadas de Matemática. Reconhecida por mérito docente pela sua atuação na preparação de equipes para as olimpíadas de matemática por intermédio da coordenação da Olimpíada Cearense de Matemática (UFC). Correio eletrônico: anapaularasantos@gmail.com
** Doutor com ênfase no ensino da Matemática (UFC), pós-doutoramento em andamento pela Universidade Trás-os-Montes e Alto Douro (UTAD-Portugal). Coordenador e docente do Programa de Pós-Graduação em Ensino de Ciências e Matemática – PGECM/IFCE (acadêmico). Docente do mestrado profissional em Educação Tecnológica – IFCE. Professor Permanente da Universidade Federal do Ceará. Brasil. Correio eletrônico: fregis@ifce.edu.br
Resumo
Nesse artigo, pretende-se apresentar um recorte parcial de uma investigação de mestrado, no qual se descrevem, de modo específico, duas fases determinadas pela Engenharia Didática – ED no contexto das olimpíadas de matemática. Assim, apresentam- se as etapas de análises preliminares e a construção de situações olímpicas/ análise à priori. Enfatiza-se uma situação olímpica que é descrita/estruturada com o amparo do software GeoGebra. A intervenção realizada pela exploração apropriada de softwares proporciona ao aprendiz oportunidades de ultrapassar determinadas dificuldades/entraves a um entendimento ou até mesmo, à construção conceitual em geometria. Nesse sentido, a referida situação olímpica foi vivenciada por alunos do nono ano do ensino fundamental II, de uma escola privada do estado do Ceará,Brasil. A situação olímpica descrita propõe a possibilidade da construção das relações métricas no triângulo retângulo, conteúdo referente a área da geometria plana. A ED apresenta-se nessa investigação, em uma visão de complementaridade que utiliza a teoria das situações didáticas – TSD. Desse modo, a situação olímpica descrita representa uma alternativa para aulas direcionadas às olimpíadas de matemática, sua indicação e estruturação, descreve elementos atinentes à mediação didática durante o processo de ensino e aprendizagem, os quais enfatizam pormenores que possibilitam controlar e prever as possíveis ações dos estudantes, assim como, proporcionar a vivência de situações didáticas mais significativas para o estudo da geometria no contexto olímpico.
Palavras chaves: engenharia didática, Geogebra, olimpíadas de Matemática, teoria das situações.
Abstract
In this article, we intend to present a partial cut of a master's research, in which we describe, in a specific way, two phases determined by Didactic Engineering - ED in the context of the Mathematical Olympiads. Thus, we have the stages of preliminary analyzes and the construction of Olympic situations/a priori analysis. We emphasize in an Olympic situation that is described/structured with the support of GeoGebra software. Intervention through the proper exploitation of software provides the learner with opportunities to overcome certain difficulties/obstacles to an understanding or even conceptual construction in geometry. In this sense, the mentioned Olympic situation was experienced by students of the ninth year of elementary education II, from a private school in the state of Ceara, Brazil. The Olympic situation described proposes the possibility of the construction of metric relations in the triangle rectangle, content referring to the area of plane geometry. The ED is presented in this research, as a vision of complementarity that uses the theory of didactic situations - TSD. In this way, the described Olympic situation represents an alternative to classes directed to the math Olympics, their indication and structure, describes elements related to didactic mediation during the teaching and learning process, which emphasize details that make it possible to control and predict the possible student’s actions, as well as, to provide the experience of more significant didactic situations for geometry study in the Olympic context.
Keywords: didactic engineering, GeoGebra, mathematical Olympiads, theory of situations.
Resumo
En este artículo, presentamos un avance parcial de una investigación de maestría, en el que se describen, de modo específico, dos fases determinadas por la ingeniería didáctica (ID) en el contexto de las olimpiadas de matemáticas. Así, se presentan las etapas de análisis preliminares y la construcción de situaciones olímpicas/análisis a priori. Enfatizamos en una situación olímpica que es descrita/estructurada basados en el software GeoGebra. La intervención realizada explorando de manera apropiada el software, proporciona al aprendiz oportunidades de superar ciertas dificultades/ obstáculos para la comprensión o incluso, para la construcción conceptual de la geometría. En ese sentido, la referida situación olímpica fue vivenciada por alumnos de noveno grado de secundaria, de una escuela particular del estado de Ceará, Brasil. La situación olímpica descrita propone la posibilidad de la construcción de relaciones métricas en el triángulo rectángulo, contenido referente al área de la geometría plana. La ID se presenta en esa investigación desde una perspectiva de complementariedad que utiliza la teoría de las situaciones didácticas (TSD). De este modo, la situación olímpica descrita representa una alternativa para las clases dirigidas a las olimpiadas de matemáticas, su indicación y estructuración, describe elementos relativos a la mediación didáctica durante el proceso de enseñanza y aprendizaje, que enfatizan detalles que posibilitan el control y la prevención de las posibles acciones que emprenderán los estudiantes, así como, proporciona la vivencia de situaciones didácticas más significativas para el estudio de la geometría en el contexto olímpico.
Palavras chave: geoGebra, ingeniería didáctica, olimpiadas de matemáticas, teoría de las situaciones.
Introdução
As olimpíadas de Matemática estão cada vez mais conquistando espaço dentro das escolas brasileiras. Observa-se uma crescente participação dos alunos nas competições nacionais e regionais a cada ano. Isso ocorre porque essas competições, em si, não exigem do aluno, memorizações de fórmulas e o conhecimento total da disciplina, mas apenas o conhecimento de alguns conceitos básicos, um raciocínio ágil e determinada criatividade (MARTINS, 2015 p. 13). Ademais, este crescente interesse pelas olimpíadas de matemática advém dessas competições promoverem um meio de divulgação entre as escolas quando têm seus alunos premiados (BADARÓ, 2015 p.10). Assim como, também podemos destacar que as escolas que participam das olimpíadas de matemática, disponibilizam aos estudantes e aos professores uma coleção de problemas estimulantes e desafiadores (ALIEVI, 2013 p. 10; CARVALHO, 2013 p. 7). Vale ressaltar que as olimpíadas de matemática a que este artigo faz referência é a Olimpíada Brasileira de Matemática (OBM) e a Olimpíada Brasileira de Matemática das Escolas Públicas (OBMEP).
Diante desse cenário, este artigo propõe uma alternativa estruturada para trabalhar com turmas olímpicas compostas por alunos do Nível 2 (oitavo e/ou nono anos), apresenta-se uma situação olímpica, na qual utiliza-se como metodologia de ensino a teoria das situações didáticas (TSD) de Brousseau. A TSD foi desenvolvida por GUY BROUSSEAU (1986), pesquisador francês da Universidade de Bordeaux. Essa metodologia de ensino permite criar um modelo de ensino o qual suscita a interação entre o professor, o aluno e o conhecimento matemático. Ademais, a investigação descrita neste trabalho, tem como metodologia de pesquisa a Engenharia Didática (ED). A noção de engenharia didática obteve o seu ápice nos anos 80 na didática da matemática em França. Segundo ARTIGUE apud ALMOULOUD (2007 p. 17), a ED vista como metodologia de pesquisa é caracterizada por um esquema experimental com base em realizações didáticas em sala de aula.
A proposta deste trabalho é apresentar uma situação olímpica, na qual o aprendiz tem a oportunidade de vivenciar as quatros etapas da TSD (ação, formulação, validação e institucionalização) modelada pelo software Geogebra. Vale ressaltar, que para a construção dessa situação olímpica, o pesquisador utilizou como alicerce da sua investigação as duas primeiras fases da ED (análises preliminares e análise a priori). As próximas seções do artigo apresentam uma síntese da referida investigação.
Objetivos da Investigação
O problema da investigação surgiu diante da necessidade de se promover situações didáticas que se apliquem no contexto das olimpíadas de matemática. Neste sentido, a elaboração/concepção deste problema aponta obstáculos/entraves que se propõe solucionar ou, pelo menos compreender e, se possível, reproduzir em outras situações. Portanto, destaca-se o objetivo de desenvolver uma engenharia didática que permita a descrição de situações olímpicas envolvendo a construção e aplicação de conceitos referentes à geometria plana. Para alcançar este objetivo geral estabelece-se ainda os seguintes objetivos específicos: descrever uma ED sob o ponto de vista metodológico da teoria das situações didáticas (TSD), voltado ao ensino de olimpíadas de matemática; utilizar o software GeoGebra como recurso tecnológico com o intuito de suscitar o raciocínio intuitivo durante a resolução das situações olímpicas.
Vale ressaltar que no decorrer de todo o processo investigativo, a partir do momento que se planeia o percurso da pesquisa, adota-se os pressupostos da ED e assume-se determinadas hipóteses de trabalho, a saber: a TSD possibilita perspectivar as olimpíadas de matemática como uma proposta metodológica de ensino; O software GeoGebra possibilita a exploração e visualização dos elementos matemáticos presentes nas situações olímpicas.
Alguns pressupostos assumidos durante a investigação
A metodologia de pesquisa aplicada nessa investigação é a Engenharia Didática – ED. Para ALVES (2016a p. 70), a ED apresenta dois níveis de pesquisa – microengenharia e macroengenharia. Sendo assim, estabelece-se as seguintes especificações, a investigação em microengenharia se apropria das relações existentes nos fenômenos que ocorrem em sala de aula, portanto esse nível de investigação tem uma visão mais limitada. No segundo nível, depara-se com entraves/dificuldades de ordem metodológica e/ou institucionais, busca uma visão mais ampla.
A pesquisa proposta neste artigo é uma microengenharia, que busca desenvolver uma ED no ensino das olimpíadas de matemática relativo ao conteúdo das relações métricas no triângulo retângulo – geometria plana. Essa ED apresenta também variáveis macrodidáticas e variáveis microdidáticas. Para ALMOULOUD (2007 p. 175) as variáveis macrodidáticas referem-se à organização global da ED, enquanto que as variáveis microdidáticas se apresentam especificadamente na fase da experimentação da ED.
Ademais, essa ED se apoia, na metodologia de ensino denominada de teoria das situações didáticas – TSD (BROUSSEAU, 1998). Sendo assim, a situação olímpica proposta deve ser explorada durante as aulas de preparação para as olimpíadas de matemática, conforme as dialéticas estabelecidas por Brousseau – ação, formulação, validação e institucionalização.
Um pormenor fundamental a mencionar é que a TSD oportuniza a construção de um ambiente que fomenta a investigação em matemática de tal forma que os alunos podem reproduzir, mesmo que de maneira elementar, o caminho semelhante ao de um matemático na formulação de suas conjecturas. Além disso, podem surgir um conjunto de ações capazes de proporcionar mudanças nos comportamentos dos alunos e, vale ressaltar que tais mudanças caracterizam uma aprendizagem mais significativa (ALMOULOUD, 2007 p. 33).
Contudo, nesse artigo enfatiza-se apenas às fases – análises preliminares e análises à priori – construção de situações olímpicas, que permitem realizar a construção da situação didática no contexto do estudo de conceitos geométricos. Em sincronia com a sistematização prevista pela ED (ARTIGUE, 1988) e apoderando-se das pesquisas recentes nessa área, apresenta-se na próxima seção, um estudo da organização matemática e do objeto matemático de interesse que colaboraram para a definição do problema e hipóteses da pesquisa.
A Engenharia Didática e as suas diferentes fases
A Engenharia Didática vista como metodologia de pesquisa é caracterizada por um esquema experimental que proporciona a construção, execução e análise de sessões de ensino em sala de aula (ALMOULOUD, 2007 p. 171). Para ARTIGUE (1988), é uma forma de desenvolver um trabalho em sala de aula, similar ao trabalho de um engenheiro que deve se apoiar em conhecimentos específicos da área, assim como também, deve trabalhar com elementos que tenham maior complexidade.
A ED é constituída por fases distintas, a saber: as análises prévias ou preliminares, análise a priori, experimentação, análise a posteriori e validação.
As análises preliminares ou prévias no contexto olímpico
Um dos objetivos das análises preliminares é identificar os problemas decorrentes no processo de ensino e aprendizagem do objeto de estudo e esquematizar os problemas, as hipóteses, os objetivos e os fundamentos teóricos e metodológicos da pesquisa. Portanto, o pesquisador esteve atento aos seguintes pormenores: estudar a gênese histórica do objeto de estudo, analisar a estrutura matemática do saber investigado, analisar o ensino atual e seus efeitos, evidenciar os conhecimentos prévios do aprendiz em relação ao saber visado; analisar o contexto de que depende a construção e realização de cada sessão de ensino (ALMOULOUD, 2007 p. 172).
No que concerne a análise do objeto matemático escolhido (ALMOULOUD, 2007 p. 173), deve-se: estudar a evolução do tratamento do conceito a ser estudado; analisar livros didáticos enfatizando aspectos, tais como: os obstáculos que podem ser superados ou não, fundamentando a sua justificativa, o papel da história e da epistemologia levado em consideração no estudo do objeto matemático e as concepções possíveis que os aprendizes podem desenvolver, assim como também, fazer uma análise das tarefas propostas pelos autores (efeitos do contrato didático e transposição didática). Analisar as concepções de alunos e professores em relação ao objeto de estudo. Nessa fase, também é relevante, fazer um levantamento de referências bibliográficas.
Conforme ARTIGUE (1988), cada uma dessas fases pode ser retomada conforme a necessidade do pesquisador. Esse pormenor permite o pesquisador realizar um trabalho concomitante com as demais etapas da pesquisa.
Portanto, as análises preliminares correspondem a primeira fase do desenvolvimento de um quadro teórico de uma pesquisa fundamentada na ED. Nessa fase deve-se identificar as variáveis microdidáticas e/ ou macrodidáticas que serão explicitadas e manipuladas nas fases seguintes: a construção da sequência didática e análise à priori (ALMOULOUD, 2007 p. 174). Para tanto, deve-se analisar o material didático utilizado em turmas de preparação para as olimpíadas de matemática, as diferentes instituições de ensino em que o saber deve ser ensinado/aprendido e analisar a evolução do tratamento do conceito, realizar ainda uma análise praxeológica de tipos de tarefas propostas e seus possíveis efeitos do contrato didático e de transposição didática, assim como também realizar um estudo dos principais problemas relacionados com o processo de ensino e aprendizagem da noção estudada (estudo da geometria).
Primeiramente, analisou-se o material disponível em internet, livros nacionais e internacionais, manuais de preparação, banco de questões de provas, o material do POTI (pólo olímpico de treinamento intensivo) e revistas Eureka. Com esta análise buscou- se perceber a abordagem dos conteúdos de Geometria no contexto da matemática olímpica, assim como, buscou-se identificar problemas olímpicos que possam desenvolver potencialidades de aprendizagem com o auxílio do software GeoGebra.
Análise de livros e dissertações do PROFMAT direcionadas às olímpiadas de matemática
Descreve-se na tabela 1, o resultado da análise de quatro livros que comumente são utilizados durante a preparação de alunos para as olimpíadas de matemática.
Tabela 1. Análise de livros direcionados às olimpíadas de matemática.
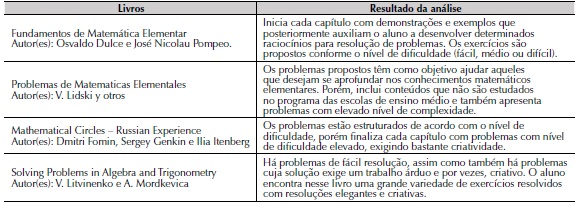
Fonte: elaborado pelos autores.
No que concerne aos livros selecionados para a análise destaca-se uma similiralidade entre a abordagem do conteúdo matemático, verifica- se que os autores seguem mesma sequência didática: Teoria (demonstração) – exploração de situações-problemas.
Nessa investigação descreve-se a análise das dissertações do PROFMAT que abordam o tema olimpíadas de matemática, totalizando vinte dissertações, dentre as quais apresenta-se os objetivos das dissertações selecionadas para serem mencionadas neste artigo, com o intuito de fazer uma conexão entre esses objetivos e a razão que fomentou o desenvolvimento de investigar sobre essa temática. BADARÓ (2015) apresenta uma proposta que ajuda o professor e aos gestores escolares a organizarem um curso preparatório para alunos que desejem participar dessas competições. MARTINS (2015) tem o objetivo de enfatizar conceitos geométricos que ao serem explorados representam entraves/dificuldades para o aprendiz. BONFIM (2013), Valessa, Z.F.S CARVALHO (2013), DOCARMO NETO (2014) e ALIEVI (2013) em suas dissertações destacam a produção de blocos de exercícios separados por semelhança de conteúdos programáticos, nos quais tem como objetivo mostrar as várias alternativas de resoluções. Já, Márcio M. CARVALHO (2013) na sua dissertação intitulada por “Resolução de problemas matemáticos olímpicos: uma abordagem aritmética modular”, apresenta soluções de problemas presentes em provas de olimpíadas de matemática de países como a França, Croácia, Espanha, dentre outros; o objetivo do seu trabalho é compreender a abordagem da aritmética modular na relação de congruência no conjunto dos inteiros para a resolução de problemas olímpicos. ALVES (2010) analisa o impacto da Olimpíada de Matemática para alunos das escolas públicas. COCCO (2013), analisa a olimpíada de matemática das escolas públicas – OBMEP, a fim de verificar se ela se constitui como uma política educacional de avaliação em larga escala. CALAZANS (2014) e BRAGANÇA (2013) investigam as possibilidades da elaboração de um material de suporte e apoio aos interessados em implantar um centro de estudo, pesquisa e preparação para olimpíada de matemática. ARAÚJO (2014) faz uma análise crítica das provas de primeira fase da OBMEP – nível 1. Mediante o resultado da análise das investigações mencionadas – dissertações do PROFMAT – observou-se que essas pesquisas não têm como objetivo desenvolver o raciocínio matemático do aluno através da vivência de uma nova metodologia que se diferencie da tradicional e/ ou até mesmo utilizar uma ferramenta tecnológica.
Portanto, na pesquisa descrita neste artigo, prioriza- se o raciocínio lógico-dedutivo, a elaboração e realização de estratégias, com o intuito de desenvolver habilidades e competências que permitam os estudantes construírem o conhecimento, a suscitar o raciocínio matemático, a reflexão, a análise, e sobretudo a descoberta através do estímulo de algumas ações, para isso adotamos a Teoria das Situações Didáticas (TSD) como metodologia de ensino.
A construção da situação olímpica e a análise à priori
Nessa fase o pesquisador elaborou, construiu e analisou uma sequência de situações didáticas com o intuito de responder as questões e validar as hipóteses determinadas nas análises preliminares. Sua função principal é a utilização de novos objetos matemáticos através de questionamentos explicitados pelos alunos no momento da resolução da situação olímpica (ALMOULOUD, 2007 p. 174).
Portanto, é nesta fase que a situação olímpica é construída. Conforme OLIVEIRA (2016), situações olímpicas são situações de ensino para resolução de problemas olímpicos segundo as fases dialéticas do BROUSSEAU (1986) que chamaremos de situação didática olímpica ou, resumidamente, situação olímpica.
Segundo ALMOULOUD (2007, p. 174), a construção dessa situação deve levar em consideração os seguintes aspectos:
• Os estudantes ao se debruçarem sobre a situação olímpica, entendem facilmente os dados da situação-problema proposta e podem se empenhar na resolução, usando os seus conhecimentos prévios.
• Essa situação olímpica deve colocar em jogo o conceito que se deseja construir e no qual o conhecimento está inserido;
• Os conhecimentos prévios dos alunos são insuficientes para a construção do novo saber, ou seja, precisam buscar/construir novos conhecimentos com o intuito de solucionar a situação olímpica;
• A situação olímpica pode envolver vários conhecimentos: geometria, álgebra, aritmética, dentre outros.
• Vale ressaltar que a situação olímpica selecionada tem como objetivos:
• Mediar os estudantes na construção de conceitos de uma forma mais significativa;
• Desenvolver habilidades tais como, a leitura, interpretação e a utilização das diferentes simbologias/ representações matemáticas, assim como também desenvolver o raciocínio lógico e dedutivo;
Estimular o raciocínio intuitivo através da modelagem da situação olímpica feita através do software GeoGebra.
Destaca-se que a situação olímpica deve ser concebida com o objetivo de fomentar nos alunos a ação, a reflexão, a elaboração de conjecturas e a autonomia. Pois, o professor deve exercer o papel de mediador e orientador (ALMOULOUD, 2007 p. 174). Segundo ARTIGUE (1995a), a situação didática (situação olímpica) deve ser concebida de tal forma que é possível prever o comportamento dos alunos.
Na análise realizada durante a primeira fase da ED, denominada de análise prévia ou preliminar, selecionou-se situações olímpicas adequadas ao uso do software Geogebra na elaboração de conjecturas das possíveis soluções dos problemas propostos e que suscitaram os conhecimentos prévios dos alunos. Ou seja, as situações olímpicas propostas têm o objetivo de construir o novo conhecimento a partir de conhecimentos antigos, esse pormenor permite a mobilização de conhecimentos matemáticos. Sendo assim “o aluno aprende adaptando-se a um meio que é um fator de contradições, de obstáculos, de desequilíbrios. Este saber proveniente da adaptação do aluno, revela-se através de respostas novas, que representam a aprendizagem” (BROUSSEAU, 1996a, p.49). Nesse sentido, ALVES (2016b) afirma que:
Diante do movimento ou um conjunto de modificações necessárias que devem ser efetivadas para que uma ação de ensino aconteça, não podemos desconsiderar a natureza intrínseca dos conteúdos, dos objetos matemáticos e dos processos matemáticos que buscamos tornar evidentes numa determinada proposta de abordagem (p. 137).
Sendo assim, a situação olímpica proposta trata do estudo da geometria, explora um teorema que frequentemente está presente em provas de olimpíadas de matemática, busca realizar uma transposição didática através da utilização do software Geogebra.
Descrição e elaboração da situação olímpica
A situação olímpica apresentada neste artigo é um problema selecionado de uma prova da Olimpíada Brasileira de Matemática (OBM) – Nível 2 (segunda fase). Para ALMOULOUD (2007), a análise à priori é de fundamental importância,
De sua qualidade depende o sucesso da situação- -problema; ademais, ela permite, ao professor poder controlar a realização das atividades dos alunos, e também, identificar e compreender os fatos observados. Assim, as conjecturas que vão aparecer poderão ser consideradas, e algumas poderão ser objeto de um debate científico em sala de aula. (ALMOULOUD, 2007, p. 176).
Partindo deste pressuposto, o professor tem o ambiente adequado para auxiliar os aprendizes a obter êxito identificando, pelo menos, uma estratégia de solução.
A seguir apresenta-se ainda, os procedimentos necessários e as possíveis estratégias que podem ser realizadas através da construção geométrica visualizada no software GeoGebra.
Situação Olímpica (OBM - 2.ª Fase/ Nível 2 – 2012): O grande artilheiro Tornado está prestes a fazer o gol mais bonito de sua carreira. Ele está de frente para o gol e apenas o goleiro está entre ele e a trave. Ele está a x metros do goleiro que, por sua vez, se encontra a 2 metros da linha do gol, onde Tornado deseja que a bola caia após passar por cima do goleiro. Em um gol dessa magnitude, a trajetória da bola deve ser uma semicircunferência. Tornado sabe que a bola deve passar a exatamente 3 metros de altura do solo quando ela estiver acima do goleiro. Qual a distância de Tornado até o goleiro, ou seja, x em metros?
Conhecimentos prévios: Semelhança de triângulos, proporção, equações do 1.° grau com uma variável.
Dialética da ação: Nesta etapa os estudantes se depararam com um problema cuja a solução é o conhecimento a ser ensinado; os alunos agiram sobre essa situação, obtendo feedback sobre sua ação. Ou seja, uma situação olímpica adequada deve permitir aos alunos “ julgar o resultado de sua ação e ajustá-lo, se necessário, sem a intervenção do professor, devido à retroação do milieu” (ALMOULOUD, 2007 p. 37).
Portanto, essa fase é caracterizada pela ação inicial dos aprendizes que ao se debruçarem sobre o enunciado da situação olímpica proposta, leram atentamente para interpretá-la corretamente, e assim analisaram e extraíram as informações do problema e posteriormente, realizaram as suas conjecturas.
Alguns alunos apresentaram dificuldades/entraves em interpretar a situação olímpica. Verificou-se que alunos que não tinham habilidades com o software GeoGebra, iniciaram a construção geométrica com lápis e papel, vale ressaltar que os aprendizes foram orientados a utilizar o GeoGebra (Figura 1.)
Figura 1. Dialética da ação.
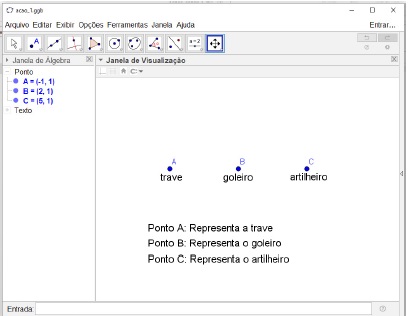
Fonte: elaborado pelos autores.
Dialética de Formulação: Esta fase, caracteriza- se pela troca de informações entre os alunos e/ou entre os alunos e o professor, essa troca de ideias pode ser da forma escrita ou oral. “Como resultado, essa dialética permite criar um modelo explícito que pode ser formulado com sinais e regras comuns, já conhecidas ou novas” (ALMOULOUD, 2007 p. 38). Destaca-se que nesta etapa, os estudantes apresentaram as ideias e estratégias adotadas durante o processo de busca da solução do problema. Para se alcançar este objetivo, o professor promoveu a interação entre os alunos. Por exemplo, se o aluno deve agir e não dispõe de toda a informação necessária, seu colega pode auxiliá-lo, complementando com o que lhe falta.
A dialética de formulação permitiu ao aluno construir, gradativamente, a elaboração da estratégia que possibilitou solucionar o problema em questão. Nesta fase, o professor instigou os alunos a analisarem a representação da situação olímpica construída com o auxílio do software GeoGebra (Figura 2).
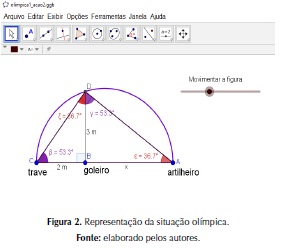
Partindo dessa construção (Figura 2), os alunos analisaram as relações matemáticas existentes entre os elementos matemáticos, resgatando os seus conhecimentos prévios (Figura 3).
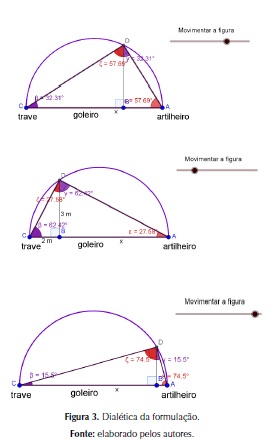
Ademais, os alunos identificaram os triângulos
semelhantes e a relação de proporcionalidade
entre os seus lados. Ao identificar os elementos
matemáticos envolvidos na situação didática, com
a interatividade e simulação de situações, os estudantes
verificaram que qualquer que seja a posição
do ponto D sobre o semicírculo (Figura 3),
os ângulos ![]() são congruentes, assim como
também os ângulos
são congruentes, assim como
também os ângulos ![]() . Partindo desse pressuposto,
inferiram que pelo caso de semelhança de
triângulo Ângulo-Ângulo (A.A), os triângulos
. Partindo desse pressuposto,
inferiram que pelo caso de semelhança de
triângulo Ângulo-Ângulo (A.A), os triângulos ![]() e
e ![]() são semelhantes. A partir desse momento,
elaboraram as estratégias para determinar o valor
de x que representa a distância entre o Tornado
e o goleiro.
são semelhantes. A partir desse momento,
elaboraram as estratégias para determinar o valor
de x que representa a distância entre o Tornado
e o goleiro.
De acordo com as conclusões elaboradas pelos alunos (Figura 4), temos:
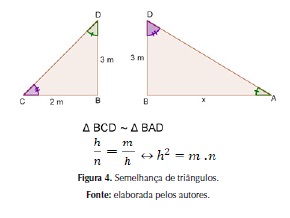
Dialética da validação: Nesta etapa, os alunos apresentaram a estratégia que os levaram a solucionar o problema, ou seja, mostraram a validade do modelo criado. Outro pormenor importante é o de justificar a eficácia do seu modelo. Assim, os alunos foram submetidos à análise de todos que o escutavam, podendo ter que dar mais explicações diante das possíveis indagações por parte dos colegas que podem não entender ou discordar. Assim, o professor promoveu um debate entre os alunos, com o objetivo de estabelecer provas ou de refutá-las. O debate sobre a certeza das conclusões permite organizar as interações com o milieu, validando as estratégias que possam permitir solucionar o problema (ALMOULOUD, 2007 p. 38).
Em relação à solução da situação olímpica, verificou- se que é crucial descobrir os triângulos semelhantes, aplicando corretamente a proporcionalidade entre os seus lados homólogos. Da turma de alunos que participaram dessa aula, três estudantes confundiram- se e apresentaram dificuldades em identificar os lados homólogos, consequentemente apresentando erros na resolução. Entretanto, o professor interviu para auxiliar os alunos a validar a estratégia adotada através da interatividade da construção feita no ambiente do software GeoGebra, utilizando os conhecimentos algébricos necessários para aplicar o caso de semelhança de triângulos.
A seguir, os alunos demonstraram o teorema (Figura 5) e apresentaram no quadro com a mediação do professor, de uma forma geral, o enunciado: “a medida da altura relativa à hipotenusa é média geométrica (ou média proporcional) entre as medidas das projeções dos catetos sobre a hipotenusa.”
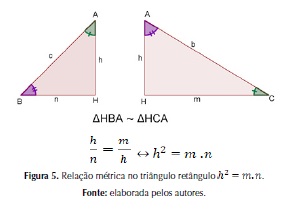
Dialética da institucionalização: Esta etapa é caracterizada pela exposição do novo conhecimento pelo professor, de forma clara e explícita. O professor previu o momento adequado para formalizar o novo conhecimento. Segundo ALMOULOUD (2007), se a institucionalização desse novo conhecimento for feita muito cedo, o seu significado será interrompido, impedindo uma aprendizagem adequada e produzindo dificuldades no seu entendimento. Assim como, quando feita de forma tardia, ela atrasa a aprendizagem e dificulta a compreensão e assimilação por parte dos alunos. A institucionalização realizou-se através do diálogo entre alunos e professores para sedimentar o novo conhecimento. O professor institucionalizou o novo saber no momento adequado, tornou-o patrimônio da turma e mostrou que esse novo conhecimento pode ser utilizado na resolução de outros problemas matemáticos (BROUSSEAU, 1986).
Sendo assim, verificou-se a oportunidade de vivenciar as etapas estabelecidas pela TSD, descrevendo situações didáticas que auxiliem os alunos a desenvolver a capacidade de resolver problemas de forma autônoma, reflexiva e colaborativa.
Considerações Finais
Esse artigo buscou perspectivar uma alternativa de ensino voltada às olimpíadas de matemática. Apresentou uma situação olímpica vivenciada por uma turma constituída por oito alunos, do nono ano do Ensino Fundamental II, de uma escola privada do estado do Ceará, Brasil.
Adotou-se como metodologia de pesquisa a Engenharia Didática (ED), a qual permitiu a análise e preparação do campo epistêmico relacionado ao objeto a ser estudado. Ao seguir os seus pressupostos, o pesquisador estabeleceu os objetivos e as hipóteses da sua investigação. Sendo assim, destaca-se na construção da situação olímpica, um maior rigor e solidez adquiridos pelo pesquisador em construí-la e aplicá-la, utilizando a Teoria das Situações Didáticas (BROUSSEAU, 1986). Realizar uma aula seguindo as dialéticas estabelecidas por Brousseau (ação, formulação, validação e institucionalização) com o amparo do software GeoGebra, a partir da modelização do problema olímpico, permitiu a inclusão de um conjunto maior de estudantes ao ambiente de discussão visando a elaboração de conhecimentos matemáticos. Ademais, propõe ao professor de Matemática perspectivar novas formas de abordagem (com o uso da tecnologia) e descrição de situações olímpicas, que não sejam restritas a uma atividade de resolução de problemas, com tempo previamente demarcado e predominantemente individuais.
Destaca-se ainda que, no momento da validação (Figura 5), o professor interviu para que os alunos generalizassem a relação métrica no triângulo retângulo encontrada para solucionar o problema. Portanto, a situação olímpica proposta permitiu aos alunos ao mesmo tempo que solucionassem o problema, construíssem a demonstração de um teorema.
A situação olímpica apresentada suscitou nos alunos, a elaboração de conjecturas, a visualização de elementos matemáticos envolvidos, estruturar estratégias, testá-las e validá-las. Diferentemente do material didático disponível à preparação dos alunos para as olimpíadas de matemática (OBM e OBMEP), nos quais os seus autores apresentam demonstrações, utilizando o rigor e a formalidade exigida pela matemática, acompanhada de uma variedade de exercícios, sem adotar uma metodologia de ensino que desenvolva o raciocínio matemático. O software GeoGebra é utilizado nesse trabalho como ferramenta que permitiu aos alunos analisarem e visualizarem através de simulações, às conjecturas e estratégias escolhidas como solução do problema. Dessa forma, os alunos percorreram o mesmo caminho que o matemático vivencia ao realizar as suas investigações. Ao resolver um problema, há diversas estratégias que podem levar a solução, as quais com a mediação adequada do professor, os alunos têm a possibilidade de selecionar a melhor estratégia. Sendo assim, os estudantes tiveram a oportunidade de construir o conceito, demonstrá-lo e validá-lo.
Portanto, este artigo apresentou uma situação olímpica, dentre algumas que estão sendo construídas e validadas pelo pesquisador, com o intuito de fomentar a compreensão dos conceitos geométricos na elaboração da solução de problemas, direcionando o ensino de olimpíadas não apenas para alunos reconhecidos como mais habilidosos no estudo da Matemática; Promovendo a socialização dos conhecimentos matemáticos, tornando os estudantes mais autônomos e colaborativos entre si.
Referências
ALIEVI, P. T. Soluções não clássicas para problemas da OBMEP. 47p. Dissertação (Mestrado Profissional em Matemática – PROFMAT). Universidade Federal de Santa Maria, Rio Grande do Sul, 2013.
ALMOULOUD, S.A. Fundamentos da Didática da Matemática. Editora UFPR. São Paulo: Brasil. 2007.
ALVES, W.J.S. O Impacto da Olimpíada de Matemática em Alunos da Escola Pública.30p. Dissertação (Mestrado Profissional em Ensino de Matemática - PROFMAT). Pontifícia Universidade Católica de São Paulo – PUC, São Paulo, 2010.
ALVES, F.R.V. Insight: descrição e possibilidades de seu uso no ensino do cálculo. VIDYA, Santa Maria, v. 32, n. 2, pp. 149-161, jul./dez. 2012.
ALVES, F.R.V. Engenharia Didática para a generalização da sequência de Fibonacci: uma experiência num curso de licenciatura. Educ. Matem. Pesq., São Paulo, v. 18, n. 1, pp. 61- 93. 2016a.
ALVES, F.R.V. Didática de matemática: seus pressupostos de ordem epistemológica, metodológica e cognitiva. Interfaces da Educação, v.7, n.21, p. 131-150, Paranaíba: Brasil. 2016b.
ARAÚJO, R.R. Perfil de desempenho dos alunos de ensino médio da unidade integrada Henrique Rocha, Tutóia-MA, frente a primeira fase da OBMEP. 45p. Dissertação (Mestrado Profissional em Matemática – PROFMAT), Universidade Federal do Piauí (UFPI), 2015.
ARTIGUE, M. Ingénièrie didactique. In: Brun, J. Didactiques des Mathématiques. Paris: Délachaux et Niestle, 1995a. pp. 243-263.
ARTIGUE, M. Ingenieria Didática. In: Artigue, Michelle; Douady, Régine; Moreno, Luis; Gomez, Pedro. Ingeniéria didatica en Educacion Matemática. Grupo Editorial Iberoamericano, Bogotá: Colombia. pp. 33-61, 1995b. Disponível em: http://funes.uniandes.edu.co/676/1/ Artigue1995Ingenieria.pdf. Acessado em: 20/02/2017.
ARTIGUE, M. Ingénierie Didactique. Recherches en Didactique des Mathématiques. Grenoble: La Pensée Sauvage-Éditions, v. 9.3, p. 281-308, 1998.
BADARÓ, R.L. Do zero às medalhas: orientações aos professores de cursos preparatórios para olimpíadas de matemática. 144p. Dissertação (Mestrado Profissional em Matemática - PROFMAT). Universidade federal da Bahia, Salvador, 2015.
BONFIM, A.P. Produção e Aplicação de Material Didático para estudantes iniciantes em Olimpíadas de Matemática. 243p. Dissertação (Mestrado Profissional em Matemática – PROFMAT). Universidade Federal do Pará, Belém, 2013.
BRAGANÇA, B. Olimpíada de Matemática para a Matemática avançar. 107p.. Dissertação (Mestrado Profissional em Matemática - PROFMAT). Universidade Federal de Viçosa, Minas gerais, 2013.
BROUSSEAU, G. Les obstacles épistémologiques, problèmes et ingénierie didactique. In: Théorie des situations didactiques. Grenoble La Pensée Sauvage. Grenoble: Francia. 1998. pp. 115-160.
BROUSSEAU, G. Théorisation des phénomènes d'enseignement des mathématiques. Mathematics. Université Sciences et Technologies - Bordeaux I, 1986.
BROUSSEAU, G. Introdução ao Estudo das Situações Didáticas. 128p. Editora Ática. São Paulo, Brasil, 2008.
CALAZANS, M.V.F. Proposta de implantação do centro preparatório para olimpíadas de matemática. 40p. Dissertação (Mestrado Profissional em Matemática – PROFMAT). Universidade Estadual de Santa Cruz, Ilhéus, Bahia, 2014.
CARVALHO, Márcio M. de. Resolução de problemas matemáticos olímpicos: uma abordagem aritmética modular. 62p. Dissertação (Mestrado Profissional em Matemática – PROFMAT). Universidade Federal do Vale do São Francisco, Bahia, 2013.
CARVALHO, Valessa, Z.F.S. Funções convexas com aplicações em problemas de olimpíadas de matemática. 60p. Dissertação (Mestrado Profissional em Matemática - PROFMAT). Universidade Federal do Piauí, Teresina, 2013.
CARVALHO JÚNIOR, A.L.L. de. Material Multimídia: Resolução comentada de algumas questões do nível 3 da OBMEP sobre geometria. 64p.. Dissertação (Mestrado Profissional em Matemática – PROFMAT). Universidade Federal do Pará, Belém, 2013.
COCCO, E.M. Olimpíada de Matemática das Escolas Públicas e avaliação em larga escala: possíveis interlocuções. 161p.. Dissertação (Mestrado em Educação). Universidade Regional Integrada do Alto Uruguai e das Missões, Rio Grande do Sul, 2013.
DOCARMO NETO, V. Teorema de Pitágoras e áreas: sua aplicabilidade no banco de questões da OBMEP. 44p. Dissertação (Mestrado Profissional em Matemática – PROFMAT). Centro de Ciências da Natureza, UFPI, Teresina, 2014.
DOLCE, O.; POMPEO, J.N. Fundamentos de Matemática Elementar. Vol. 9: Geometria Plana. 456p. v. 7. Atual Editora. São Paulo: Brasil. 2008.
FOMIM, D.; GENKIN, S.; ITENBERG, I. Mathematical Circles – Russian Experience. 271p. Mathematical World. v. 7. Estados Unidos da América, 1993.
IEZZI, G.; MURAKAMI, C. Fundamentos de Matemática Elementar. Vol.1 Conjuntos e Função. 317p. 3.ed. Atual Editora. São Paulo: Brasil. 1977.
IGLIORI, S.B.C. A noção de Obstáculo Epistemológico e a Educação Matemática. In Educação Matemática Uma Introdução. Org. Silvia Machado. EDUC. São Paulo. 1999.
JACON, L.S.C; KALHIL, J.B. O professor formador e as competências em tecnologia de informação e comunicação: um estudo sobre quais recursos computacionais estes profissionais utilizam na elaboração do seu material didático. AMAZÔNIA - Revista de Educação em Ciências e Matemáticas, v. 8, n. 15 - jul. 2011/dez. p.27-44. 2011.
LACERDA, C.W.P. de. Sequências e séries: conhecendo e construindo estratégias de abordagem. Dissertação (Mestrado Profissional em Matemática – PROFMAT). Universidade Federal Rural de Pernambuco. 2014.
LAGUERRE, E. Une ingenierie didactique pour làppentisssage du theo-reme de Thales au college. Education. Universit_e Paris-Diderot - Paris VII, Français. 2005.
LITVINENKO, V.; MORDKEVICA, A. Solving Problems in Algebra and Trigonometry. Mir Publishers. Moscow: Russia. 1987.
LIDSKI, V.; OVSIANIKOV, L.V.; TULAIKOV, A.N.; SHABUNIN, M. I. Problemas de Matematicas Elementales. 3a. ed. Editorial Mir. Moscu: Russia. 1978.
LORENZATO, S. Por que não ensinar Geometria?
A educação matemática em revista. Geometria.
Blumenau, n. 04, pp. 03-13, 1995. Disponível
em:
MARTINS, R.A. Colinearidade e concorrência em olimpíadas internacionais de matemática: uma reflexão voltada para o ensino da geometria. 2015. Dissertação (Mestrado Profissional em Matemática – PROFMAT). Universidade Federal de Brasília.
NETO, A.C.M. Geometria Plana. Tópicos de matemática elementar, vol.2. Coleção professor de matemática, SBM. 2013.
OLIVEIRA, C.C. do N. Olimpíadas de Matemática: concepção e descrição de “situações olímpicas” com o recurso do software Geogebra. 136 p. Dissertação (Mestrado em Ensino de Ciências e Matemática) - Centro de Ciências, Universidade Federal do Ceará, Fortaleza, 2016.
OLIVEIRA, E.C. de; CHIUMMO, A. Análise da aprendizagem de semelhança de triângulos por alunos de graduação em Matemática. VIDYA, Santa Maria, v. 35, n. 2, p. 179-195, jul./dez., 2015.
Licencia
Góndola, Ens Aprend Cienc. es una publicación de acceso abierto, sin cargos económicos para autores ni lectores. La publicación, consulta o descarga de los contenidos de la revista no genera costo alguno para los autores ni los lectores, toda vez que la Universidad Distrital Francisco José de Caldas asume los gastos relacionados con edición, gestión y publicación. Los pares evaluadores no reciben retribución económica alguna por su valiosa contribución. Se entiende el trabajo de todos los actores mencionados anteriormente como un aporte al fortalecimiento y crecimiento de la comunidad investigadora en el campo de la Enseñanza de las Ciencias.
A partir del 01 de diciembre de 2018 los contenidos de la revista se publican bajo los términos de la Licencia Creative Commons Atribución–No comercial–Compartir igual 4.0 Internacional (CC-BY-NC-SA 4.0), bajo la cual otros podrán distribuir, remezclar, retocar, y crear a partir de la obra de modo no comercial, siempre y cuando den crédito y licencien sus nuevas creaciones bajo las mismas condiciones.
Los titulares de los derechos de autor son los autores y la revista Góndola, Ens Aprend Cienc. Los titulares conservan todos los derechos sin restricciones, respetando los términos de la licencia en cuanto a la consulta, descarga y distribución del material.
Cuando la obra o alguno de sus elementos se halle en el dominio público según la ley vigente aplicable, esta situación no quedará afectada por la licencia.
Asimismo, incentivamos a los autores a depositar sus contribuciones en otros repositorios institucionales y temáticos, con la certeza de que la cultura y el conocimiento es un bien de todos y para todos.





















