SISTEMAS DE NUMERAÇÃO À LUZ DE UMA ABORDAGEM HISTÓRICOEPISTEMOLÓGICA

SISTEMAS DE NUMERACIÓN A LA LUZ DE UN ENFOQUE HISTÓRICO­EPISTEMOLÓGICO

NUMBERING SYSTEMS IN THE LIGHT OF A HISTORICAL-EPISTEMOLOGICAL APPROACH

Rafael Marques Pinheiro*, Simone Luccas**, Lucken Bueno Lucas***

Cómo citar este artículo: Marques Pinheiro, R., Luccas S. y Bueno Lucas, L. (2019). Sistemas de numeração á luz de uma abordagem histórico-epistemológica. Gdola, Ensenza y Aprendizaje de las Ciencias, 14(2), 253-267. DOI: http://doi.org/10.14483/23464712.13030

Recibido: 15 de febrero de 2018; aprobado: 05 de octubre de 2018

* Mestrando em Mestrado Profissional em Ensino de Matemática pela Universidade Federal Tecnológica do Paraná – UTFPr, Londrina, Paraná, Brasil. Correio eletrônico: rafael.rmp@hotmail.com – ORCID: http://orcid.org/0000-0002-5000-2931

** Doutora em Ensino de Ciências e Educação Matemática pela Universidade Estadual de Londrina. Professora Adjunta do Colegiado de Matemática e Vice Coordenadora do Programa de Pós-Graduação - Mestrado Profissional em Ensino da Universidade Estadual do Norte do Paraná – UENP, Campus de Cornélio Procópio, Paraná, Brasil. Correio eletrônico: simoneluccas@uenp.edu.br – ORCID: http://orcid.org/0000­0002-5435-5478

*** Doutor em Ensino de Ciências e Educação Matemática pela Universidade Estadual de Londrina. Professor Adjunto do Colegiado de Ciências Biológicas e Coordenador do Programa de Pós-Graduação - Mestrado Profissional em Ensino da Universidade Estadual do Norte do Paraná – UENP, Campus de Cornélio Procópio, Paraná, Brasil. Correio eletrônico: luckenlucas@uenp.edu.br – ORCID: http://orcid.org/0000-0003-2122-8672 MARQUES PINHEIRO, R., LUCCAS S. Y BUENO LUCAS, L.

Resumo

A inclusão da abordagem histórica no ensino de conteúdos escolares vem sendo defendida nas últimas décadas por pesquisadores de diversas áreas, pois permite aos envolvidos nos processos de ensino e de aprendizagem, uma visão crítica e reflexiva acerca dos assuntos estudados, dando mais sentido ao conhecimento sistematizado e compartilhado com as novas gerações. Desse modo, o presente artigo tem por objetivo investigar o pa­pel da abordagem histórico-epistemológica como fundamentação metodológica para a elaboração de uma síntese acerca do desenvolvimento dos sistemas de numeração. Para tanto, foi realizada uma pesquisa de natureza qualitativa, mediante revisões em livros, teses, dissertações e artigos científicos que tratam do tema. Foi possível evidenciar os encaminhamentos dados por diversas civilizações frente à necessidade de empreender quantificações, até a estabilização de um sistema eficiente de numeração que superou os limites dos sistemas predecessores. A abordagem histórico-epistemológica ofereceu condições metodológicas para uma ampliação de conhecimentos relativos ao objeto de estudo, favorecendo um aprofundamento da pesquisa realizada.

Palavras chaves: história, epistemología, sistemas numéricos.

Abstract

Consider the inclusion of a historical approach to treating contents in the teaching pro­cess, has been defended in recent decades by researchers from different areas since it allows the development of critical and reflexive views by teachers and students. This improves the meaning of systematized knowledge shared with subsequent generations. Thus, the present article aims to investigate the role of the historical-epistemological approach as a methodological foundation for the elaboration of synthesis on the devel­opment of numbering systems. For this, qualitative research was carried out, through reviews in books, theses, dissertations, and scientific articles that address the same subject matter. There are pieces of evidence about referrals by many civilizations highlighting the need to undertake quantification, in order to establish a numbering system more efficient than existing systems at the time. The historical-epistemological approach of­fered methodological conditions for an increase in knowledge regarding the object of study, favouring a deepening of the research carried out.

Keywords: history, epistemology, numerical systems.

Resumen

La inclusión del enfoque histórico para el tratamiento de contenidos escolares en procesos de enseñanza, viene siendo defendida en las últimas décadas por investiga­dores de diversas áreas, pues permite a los involucrados en enseñanza y aprendizaje, una visión crítica y reflexiva acerca de los asuntos estudiados, dando más sentido al conocimiento sistematizado que se comparte con las nuevas generaciones. De este modo, el presente artículo investiga el papel del abordaje histórico-epistemológico como fundamento metodológico para la elaboración de una síntesis acerca del de­sarrollo de los sistemas de numeración. Para ello, se realizó una investigación de naturaleza cualitativa, mediante revisiones en libros, tesis, disertaciones y artículos científicos. Es posible evidenciar las propuestas de diversas civilizaciones frente a la necesidad de emprender cuantificaciones, hasta la estabilización de un sistema eficiente de numeración que superó los límites de los predecesores. El enfoque his­tórico-epistemológico ofreció condiciones metodológicas para una ampliación de conocimientos relativos al objeto de estudio, favoreciendo la profundización de la investigación realizada.

Palabras clave: historia, epistemología, sistemas numéricos.

Introdução

Conhecer e refletir sobre a natureza dos conceitos científicos vem sendo bastante discutido por pesqui­sadores, sobretudo em função de sua importância no âmbito educacional. No ensino de Ciências e Matemática, a inclusão da abordagem histórica é defendida por muitos pesquisadores (MATTHEWS, 1995; MIGUEL, MIORIM, 2011; LUCAS, 2010; MARTINS, 2007; LUCCAS, 2004; ARAMAN, 2011; dentre outros), seguindo uma perspectiva que possi­bilite a professores e alunos uma visão mais crítica do conhecimento científico, no âmbito escolar.

Diante dessas considerações, este artigo busca subsídios teóricos na História e na Epistemologia da Matemática e da Ciência para fundamentar uma abordagem mais abrangente que auxilie o desenvol­vimento de pesquisas, em âmbito metodológico, e contribua para o ensino dessas áreas.

A abordagem Histórico-Epistemológica pode ser entendida como um meio de análise das estru­turas dos conhecimentos desenvolvidos por seres humanos no decorrer de um determinado período de tempo. Nesse sentido, e se referindo especifi­camente ao conhecimento matemático, WALDO­MIRO (2011 p. 61) enfatiza que “[...] o estudo da história da Matemática altera profundamente as concepções epistemológicas do conhecimento ma­temático, assim como transforma a prática pedagó­gica da matemática”.

Diante dos apontamentos acima apresentados, o objeto de pesquisa deste artigo envolve os siste­mas de numeração, os quais foram sistematizados por diferentes povos, em diferentes épocas. Assim, buscamos responder a seguinte indagação: qual o papel de uma abordagem Histórico-Epistemológica da Ciência na constituição de uma síntese históri­co-epistemológica sobre o desenvolvimento dos Sistemas de Numeração?

Levando em conta tal questionamento, o objetivo deste artigo consiste em investigar o papel da aborda­gem histórico-epistemológica como fundamentação metodológica para a elaboração de uma síntese acer­ca do desenvolvimento dos sistemas de numeração.

Para tanto, optamos por reconstruir historicamente alguns sistemas de contagem e de numeração que foram desenvolvidos por diferentes culturas, basean­do-nos em autores como IFRAH (2010), EVES (2011), BOYER (1996) e ROQUE (2012).

1. O Papel da Abordagem Histico-Epistemolica e suas Implicaçs no Ensino

São inúmeras as potencialidades pedagógicas da História da Matemática na perspectiva do ensino e da aprendizagem da Matemática, como a con­tribuição para a desmistificação da Matemática, a explicação de alguns porquês da Matemática Ele-mentar, a apresentação da Matemática como criação humana e suas aplicações para a vida em socieda­de, dentre outras (BRASIL, 1997, 2008; MIGUEL, MIORIM, 2011).

Como já sinalizado por BARONI, NOBRE (1999) a História da Matemática é uma área do conheci­mento matemático e também um campo de inves­tigação teórico, sendo ingênuo considerá-la apenas como uma metodologia de ensino.

A História da Matemática como campo de pes­quisas em Educação Matemática vem sendo inves­tigada há mais de duas décadas no Brasil, como aponta a tese de doutorado de ANTÔNIO MIGUEL (1993). Em seu trabalho, o autor fez uma relação entre História, História da Matemática e Educação Matemática sob o ponto de vista de diferentes au­tores, além de apresentar uma proposta pedagógica a respeito dos números irracionais fazendo uso da abordagem histórica.

A História permite descobrir o porquê de de­terminados conhecimentos ou conceitos serem considerados científicos, ou até mesmo o porquê de ensiná-los no âmbito escolar, entendendo que são desenvolvidos de acordo com necessidades de grupos sociais, levando em consideração crenças e práticas de diferentes culturas.

No entanto, quando se propõe um trabalho ar­ticulando simultaneamente a abordagem histórica com aportes filosóficos, nota-se que as contribuições para os processos de ensino e de aprendizagem podem ser ainda maiores, além de torná-los mais dinâmicos. Essas ideias já foram evidenciadas por MATTHEWS (1995), ao salientar que a inserção da abordagem de cunho histórico-filosófico no ensino pode tornar as aulas mais instigantes e desafiadoras, desenvolver o pensamento crítico, relacionar os objetos estudados com o caminhar da sociedade, contribuir para o entendimento de conceitos cien­tíficos e matemáticos, dentre outros.

É por meio da Filosofia, mais especificamente da Epistemologia, que se abrem portas para a reflexão das estruturas dos conhecimentos desenvolvidos, seja do pesquisador, do professor, do aluno ou quais­quer outros envolvidos na relação ensino-aprendi­zagem em Ciências e Matemática.

Do ponto de vista do ensino, ASTOLFI, DEVE­LAY (1995) defendem que a reflexão epistêmica pode propiciar um exame da estrutura do saber a ser ensinado. Segundo os autores, o exame pode ser dado a partir de alguns questionamentos como: quais são os principais conceitos que funcionam na disciplina? Quais relações unem esses conceitos? “[...] esta reflexão epistemológica se interessa pelos métodos, princípios e conclusões de uma ciência” (ASTOLFI, DEVELAY, 1995 p. 27).

Quando se busca o desenvolvimento histórico dos conhecimentos matemáticos, pode-se perceber que em sua maioria são criados a partir de ações que visam resolver problemas do cotidiano (IFRAH, 2010; EVES, 2011; BOYER, 1996). Vale registrar que com o desenvolvimento e consolidação da Matemática enquanto área do conhecimento humano, muitos estudos passaram a ser realizados no con­texto da própria Matemática.

Ao realizar pesquisas com uma abordagem His­tórico-Epistemológica dos conteúdos matemáticos, podemos instigar estudantes a se questionarem sobre os conhecimentos matemáticos desenvolvidos no decorrer da história e isso pode favorecer o processo de aprendizagem.

Essa pode ser uma maneira inserir os discen­tes em um contexto de descobertas, de modo que as perguntas sejam o principal recurso para se construir respostas. Sendo assim, a abordagem Histórico-Epistemológica permite um olhar heurís­tico dos que buscam uma compreensão global do conhecimento estudado.

2. Procedimentos Metodolicos

A pesquisa pautou-se nos pressupostos da aborda­gem qualitativa, com revisão bibliográfica e análises reflexivas subsidiadas pelos encaminhamentos da abordagem Histórico-Epistemológica.

Segundo GODOY (1995) as pesquisas qualita­tivas buscam responder questões que envolvem as relações socais entre os seres humanos, sendo que “[...] um fenômeno pode ser melhor compreendi­do no contexto em que ocorre e do qual é parte, devendo ser analisado numa perspectiva integrada” (GODOY, 1995 p. 21).

ANDRÉ (2013) corrobora com GODOY (1995) ao salientar que as pesquisas qualitativas são reali­zadas sob um olhar que trata o conhecimento como um processo socialmente construído por meio das interações entre os sujeitos, de modo a atuarem na realidade, e ao mesmo tempo em que a transforma é transformado por ela.

Com relação à pesquisa bibliográfica GIL (2010) argumenta que pesquisas dessa natureza são reali­zadas em material já publicado. A vantagem desse tipo de pesquisa consiste em “[...] permitir ao in­vestigador a cobertura de uma gama de fenômenos muito mais ampla do que aquela que poderia se pesquisar diretamente” (GIL, 2010 p. 30).

A pesquisa bibliográfica pode ser considerada Histórico-Epistemológica a partir do momento em que se recorre a historiadores, a fim de se analisar a estrutura dos conhecimentos, seu desenvolvimento no decorrer do tempo e suas implicações.

Neste trabalho o material bibliográfico utilizado constituiu-se de livros específicos da História da Matemática, documentos oficiais que regulamentam o ensino tanto no estado do Paraná quanto no âm­bito nacional (Brasil) e, de teses e dissertações cujas pesquisas envolviam a abordagem histórico-epis­temológica. Após a seleção desse material um es­tudo detalhado de cada sistema de numeração foi realizado, especificando períodos e características atinentes a cada sistema de numeração. De posse desse conhecimento, procurou-se apresentar uma escrita sistematizando todas as características e pecu­liaridades estruturais de cada sistema de numeração.

3. Sistemas de Numeração: análise epistêmica de uma reconstrução histica

A indagação que norteou o desenvolvimento deste artigo estimulou os pesquisadores a registrarem e refletirem acerca dos passos trilhados por diferen­tes civilizações no desenvolvimento de sistemas de contagem e numeração antigos até a sistematização do sistema de numeração hindu-arábico, atualmente utilizado no Brasil.

Há aproximadamente 50.000 anos homens e mulheres, por meio de seus afazeres diários, senti­ram a necessidade de contar e registrar quantida­des. Em meio a esse contexto, diferentes culturas influenciadas ou não umas pelas outras, buscaram solucionar seus problemas fazendo uso dos mais diferentes métodos de contagem.

É razoável admitir que a espécie humana, mes­mo nas épocas mais primitivas, tinha algum senso numérico, pelo menos ao ponto de reconhecer mais ou menos quando se acrescentavam ou retiravam objetos de uma coleção pequena, pois há estudos que mostram que alguns animais são dotados desse senso. (EVES, 2011, p. 25)

Algumas comunidades usavam pedras, outras usavam entalhes em ossos (Figura 1), mas diversas culturas deixaram marcas históricas que evidenciam padrões de quantificação aplicados à solução de problemas diários, mesmo que de forma rudimentar.

É provável que a necessidade diária tenha ser­vido como uma ‘alavanca propulsora’ para o des­envolvimento de sistemas de contagens e, mais tarde, de sistemas de numeração. É possível que os conhecimentos matemáticos em sua concepção original tenham se desenvolvido a partir de neces­sidades reais ou interesses próprios daqueles que os desenvolveram.

Figura 1. Registros numéricos preservados por meio de entalhes
(Osso de Ishango¹).
Fonte: EVES (2011 p. 26).

Há milhares de anos, os números eram ‘sentidos’, ou seja, não tinham relação com a capacidade de abstração dos seres humanos. Ainda nos dias atuais, no Brasil, existem tribos indígenas que não atribuem aos números um significado independente da natu­reza dos objetos que são contados (IFRAH, 2010). Acredita-se que se essas tribos ainda não desenvol­veram sistemas de contagens mais ‘aperfeiçoados’ pelo fato de suas contagens serem suficientes para atender as necessidades cotidianas.

De acordo com PATERLINI (2008) algumas tribos indígenas das Ilhas Murray utilizavam o seguinte vocábulo para efetuar contagem: netat (um), neis (dois), neis netat (três), neis neis (quatro). Já para quantidades maiores que quatro, utilizavam o vo­cábulo ras, que significa ‘muitos’. O método de contagem dos índios dessa tribo pode revelar um tempo em que homens e mulheres possuíam uma abstração elementar se comparada aos dias atuais.

A ausência de uma abstração mais desenvolvida e a presença de certa limitação do senso numérico do ser humano são alguns fatores que podem ter contribuído para a criação de diferentes modos de contar e registrar quantidades, os quais surgiram a partir da evolução da capacidade cognitiva do ser humano.

Isso é percebido ao analisar, por exemplo, a evo­lução dos registros dos traços verticais das antigas civilizações (Quadro 1). Após perceberem os limites desses registros, criaram o princípio ternário. Não satisfeitos, mais tarde criaram o princípio quinário, usando um registro auxiliar para a quantidade cinco, o que contribuiu com a percepção visual daqueles que observavam os registros.

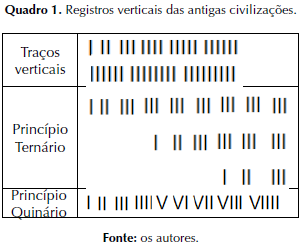
Em um estágio mais avançado, diversas culturas desenvolveram sua própria base numérica de conta­gem. Algumas usaram (ou ainda usam) a base 5, a base 10, a base 12, a base 20 e até mesmo a base 60. A base decimal é a mais usual na sociedade contemporânea.

Mas, o que realmente levou diferentes povos, em diferentes épocas, a estabelecerem as mais di­versas bases numéricas, na tentativa de suprir as necessidades de contagem? Para responder a essa indagação resta conhecer os olhares dos historiado­res, que admitem não existir uma verdade absoluta em relação a alguns fatos, talvez porque algumas fontes primárias tenham se perdido.

Por volta de aproximadamente 4.000 a.C., al­guns povos habitaram as terras da Mesopotâmia, o que permitiu que diversos modos de contar se desenvolvessem, como é o caso dos sumérios e dos babilônios. Influenciados por uma prática de con­tagem por meio de tokens e invólucros, feitos em argila, esses povos desenvolveram os algarismos cu­neiformes, que mais tarde deram origem ao sistema de numeração posicional dos babilônios (ROQUE, 2012). Assim, os sumérios inventaram o sistema de base 60 e os babilônios, o sistema posicional que continha o conceito da quantidade zero.

Na medida em que a sociedade Mesopotâmica se desenvolvia, os povos foram aperfeiçoando o modo como os tokens (pequenas unidades de argila utiliza­das para representar quantidades) eram armazenados, entre eles havia os invólucros feitos de argila (Figura 2), dentro dos quais os tokens eram guardados e fe­chados: “[...] os invólucros escondiam os tokens e, por isso, em sua superfície, eram impressas as formas contidas em seu interior” (ROQUE, 2012, p. 41).

Por volta de 3.000 a.C., já na escrita cuneifor­me, os sumérios criaram símbolos especiais para as quantidades 1, 10, 60, 600, 3.600 e 36.000 (Fi­gura 3). Nesse período houve algumas mudanças importantes, já que os cálculos começaram a ser efetuados e surgiu o sistema de posição, ou seja, o mesmo símbolo passou a representar quantidades diferentes (ROQUE, 2012).

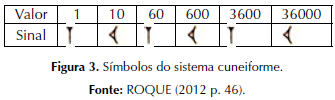
A Figura 3 apresenta a origem de um sistema posicional, ou seja, o mesmo símbolo pode repre­sentar diferentes números, dependo da posição em que ocupa na escrita. Percebe-se que o princípio de posição teve sua gênese há milhares de anos antes de Cristo, sendo um princípio que prevalece até os dias atuais, o que pode ser observado ao analisarmos a estrutura do sistema de numeração hindu-arábico.

Por mais que as representações dos números e suas bases continuassem a depender do contexto, aos poucos esses povos começaram a registrar lis­tas que apresentavam relações entre os diferentes sistemas de medida. Quando os procedimentos de conversão eram realizados em um contexto de ad­ministração da sociedade e não matemático, foi-se introduzido o sistema sexagesimal de posição dos babilônios (ROQUE, 2012).

O sistema sexagesimal possui dois símbolos, um para a unidade e outro para a dezena. Cada sessenta unidades de determinada ordem, pode ser representada por uma unidade da ordem imedia­tamente superior. Esse sistema faz uso do princípio aditivo² até a quantidade 59, se tornando um sistema posicional, a partir do momento em que se usava o mesmo símbolo da unidade para representar a quantidade sessenta e assim por diante, e também do princípio multiplicativo³ em quantidades acima de 59 (Figura 4).

Seguem alguns exemplos para a representação de números além da primeira ordem:

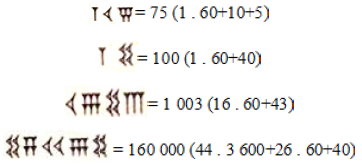
Embora seja considerado um grande avanço, o sistema de numeração dos babilônios poderia provocar várias ambiguidades, basta pensar nas representações para os números dois e sessenta e um. Os babilônios ignoraram o zero por séculos, até meados do terceiro milênio, quando introduziram um símbolo para representá-lo: ou , aliás, este é o símbolo que representa a quantidade zero mais antigo da história dos sistemas de numeração (IFRAH, 2010).

No mesmo período em que o sistema de nume­ração da Mesopotâmia desenvolveu-se o sistema de numeração dos egípcios também foi sistematizado, porém, por meio dos registros hieróglifos e não de tabletes de argila. Esse sistema, desde seu princípio parece representar números abstratos (IFRAH, 2010; EVES, 2011).

O sistema de numeração dos egípcios comporta diferentes traçados e diferentes explicações para a origem dos seus símbolos. Ele possui símbolos para a unidade e para as seis primeiras potências de dez. Por meio do princípio aditivo, os números poderiam ser escritos repetindo os símbolos quantas vezes fosse necessário (Figura 5).

Embora seja um sistema interessante, cuja es­trutura envolve o princípio aditivo e possibilita efe­tuar algumas operações elementares, a exemplo da adição, também é um sistema que apresenta limitações, principalmente ao representar numeri­camente grandes quantidades.

Por volta de 2 000 a.C., os cretenses criaram um sistema de numeração aditivo, bastante parecido com o sistema dos egípcios, sob uma base decimal. Esse sistema atribuía símbolos para a unidade e para as potências de dez. Há indícios de que ao estabelecer relações comerciais com os babilônios e egípcios, os gregos tenham sido influenciados, sobretudo na invenção do sistema de numeração. Inicialmente, os gregos utilizavam um sistema parecido com o dos cre­tenses e também parecido com o dos egípcios, já que faziam uso do princípio aditivo, sendo decimal e com símbolos para representar a unidade e as potências de dez, baseados no sistema alfabético (IFRAH, 2010).

Para evitar repetições exageradas dos símbolos, mais tarde os gregos criaram símbolos auxiliares para as quantidades 5, 50, 500 e 5 000. No século VI a.C., por meio de símbolos alfabéticos, já teriam consolidado um sistema de numeração fazendo uso de multiplicações.

A unidade passou a ser representada por um tra­ ço vertical, o número 5 pela letra (antiga forma de Pi), inicial de “pente” que significa “cinco”. A quantidade dez, letra (delta), antiga inicial de “deka”, que significa “dez”. O número 50 era representado pelo signo , uma combinação entre as letras pi e delta, que corresponde a abreviação de “pentedeka”, que significa “cinquenta”. O nú­mero 100 podia ser representado por H , (eta) inicial de “hekaton”, que significa “cem”. O número 500 consistia em uma combinação de pi e eta , correspondente à abreviação de “pentehekaton”. O milhar pela letra X (khi), inicial de “khilioi”, que significa “mil”. Combinando as letras pi e khi, o 5.000 era representado pelo signo abreviação de “pentehekaton”, “cinco mil”. O número 10 000 pela letra M (mu), inicial de “murioi”, “dez mil”. E por fim, o número 50 000 era representado pelo signo , que combina as letras pi e mu, abreviando a palavra “pentemurioi”, que significa “cinquenta mil” (IFRAH, 2010; EVES, 2011).

Para IFRAH (2010), o sistema de numeração dos gregos é considerado uma regressão histórica do ponto de vista do cálculo propriamente dito, uma vez que com a invenção dos símbolos auxiliares as possibilidades operatórias como a adição, que era possível no sistema de numeração dos egípcios, por exemplo, tornaram-se inviáveis.

Em Roma um fato similar aconteceu, já que o sis­tema de numeração criado pelos romanos também não viabilizava a realização de operações. No en-tanto, não há como negar a influência desse sistema em nossa cultura, até os dias atuais. O sistema de numeração dos romanos é aditivo e possui símbolos especiais para 1, 5, 10, 50, 500 e 1 000. O objetivo desse sistema, como aponta IFRAH (2010) era desti­nado a fazer abreviações para anotar e reter números:

Como maior parte dos sistemas da Antiguidade, a numeração romana era regida principalmente pelo princípio da adição: seus algarismos (I =1, V = 5, X = 10, L = 50, c = 100, D = 500, M = 1 000) eram independentes uns dos outros e sua justaposição implicava na soma dos valores correspondentes (IFRAH, 2010 p. 185).

São exemplos:

356 = CCCLVI
(100+100+100+50+5+1)
3827 = MMMDCCCXXVII
(1000+1000+1000+500+100+100+100+10+10+5+1+1)

Os romanos tornaram ainda mais complexo seu sistema de numeração a partir do momento que introduziram o princípio de que todo símbolo co­locado à direita de um símbolo que representa um valor maior deveria ser subtraído dele.

IV (5 – 1) ao invés de IIII
IX (9 – 1) ao invés de VIIII
XIX (10 + 10 – 1) ao invés de XVIIII
XL (50 – 10) ao invés de XXXX
XC (100 – 10) ao invés de LXXXX
CD (500 – 400) ao invés de CCCC
CM (1.000 – 100) ao invés de DCCCC

Além disso, observamos que os símbolos criados pelos romanos sofreram mudanças no decorrer dos séculos e sua gênese não está relacionada com as letras do alfabeto latino. A Figura 6 apresenta a evo­lução do símbolo que representa a quantidade 50.

A origem do sistema romano estaria relacionada a práticas ancestrais, como a do entalhe, já que eram utilizados traços em ossos. O quinto traço era sem­pre inclinado em posição ao dedo polegar da mão esquerda. A partir dele, continuavam-se os traços verticais até o décimo traço, também inclinado, mas em posição ao dedo polegar da mão direta (IFRAH, 2010). É possível observar o registro “X” que repre­senta o número dez no sistema de numeração dos romanos na Figura 7.

Por volta do século III, os chineses também cria­ram um sistema de numeração posicional antigo por meio de barras verticais e horizontais (IFRAH, 2010), como apresentado na Figura 8.

Com uma base estritamente decimal, os chineses desenvolveram representações ideográficas para as nove unidades simples, sendo que as cinco primeiras eram representadas por traços verticais justapostos. Já as quantidades 6, 7, 8 e 9 são registradas com um traço horizontal acima de barras verticais. Segundo IFRAH “[...] a partir daí os números compostos de duas ou mais ordens de unidades eram representa­dos segundo o princípio de posição” (2010 p. 244). Seguem dois exemplos:

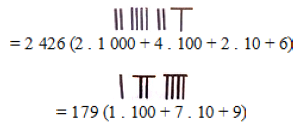
Como no babilônicos, esse sistema também ge­rava ambiguidades pelo fato de seus usuários jus­taporem o número de barras para a representação das unidades de ordens consecutivas. Por exemplo, havia uma confusão na representação dos números 5 e 23. A fim de superar essa lacuna, os chineses op­taram por criar uma segunda notação para registrar as unidades simples, “[...] formando signos análogos aos precedentes, mas desta vez com barras hori­zontais” (IFRAH, 2010 p. 245), conforme Figura 9.

Como podemos observar, as cinco primeiras uni­ dades passaram a ser representadas por barras na horizontal equivalentes a quantidade desejada. Já o número 6 “[...] por uma barra vertical encima de uma barra horizontal, e as três últimas unidades colocando abaixo do traço vertical duas, três ou quatro barras horizontais” (IFRAH, 2010, p. 245).

Para diferenciar as diversas ordens de unidades que poderiam aparecer no registro de um número, os algarismos da primeira ordem eram alternados com o da segunda e assim por diante.

As unidades da casa ímpar (unidades simples, centenas, dezenas, dezenas de milhar, milhões etc.) foram expressas por meio dos ‘algarismos verticais’ (primeira série) e as unidades de casas pares (dezenas, milhares, centenas de milhar, centenas de milhar, dezenas de milhões etc.) com ajuda dos ‘algarismos horizontais’ (segunda série). (IFRAH, 2010, p. 245)

Vejamos o exemplo na Figura 10.

Assim, os chineses sanaram as ambiguidades de modo mais eficiente que os babilônicos, porém nem todos os empecilhos foram resolvidos, uma vez que os chineses ignoraram a quantidade zero durante séculos.

Por muito tempo os sábios chineses, inventores desse sistema de posição, buscaram os mais variados recursos para suprir a necessidade do zero, como por exemplo, estabelecendo combinações entre os signos. Alguns optaram por dispor os números “[...] em quadrados, deixando uma casa vazia para cada unidade em falta” (IFRAH, 2010, p. 247).

A partir da evolução do sistema acima descrito, um novo sistema foi desenvolvido baseado funda­mentalmente nos princípios multiplicativo e aditivo. Com treze signos fundamentais, também represen­tados por palavras monossilábicas do vocabulário chinês, esse sistema de numeração possuía diversas grafias que estavam relacionadas ao contexto em que os números eram usados. A Figura 11 apresenta as grafias ditas tradicionais:

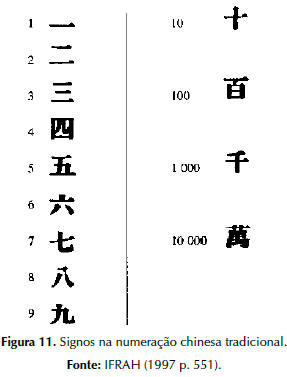
O princípio multiplicativo é associado ao sistema de numeração chinês a partir da representação da vin­tena, de modo que os trezes signos são combinados entre si. Por meio desse princípio os chineses puderam representar grandes números por uma quantidade considerável de signos, porém, ainda não era possí­vel representar todos os números inteiros a menos que novos signos fossem criados (ainda não existia o zero). Desse modo, as práticas do cálculo ficavam restritas a especialistas (IFRAH, 2010; EVES, 2011).

Os chineses contribuíram grandemente com a história dos números a partir das estruturas de seus sistemas de numeração, porém somente a partir do século VIII, influenciados pelos matemáticos e astronômicos indianos, passaram a dispor de um zero, solucionando todas as dificuldades encontra­das (IFRAH, 2010).

Já os maias, independentemente da influência de estrangeiros, fizeram descobertas parecidas por volta do primeiro século da era Cristã, desenvol­vendo um sistema de numeração de base vigesimal, posicional, com o princípios aditivo e multiplicativo e, com a presença de um símbolo para representar a quantidade zero, conforme Figura 12 (IFRAH, 2010; EVES, 2011).

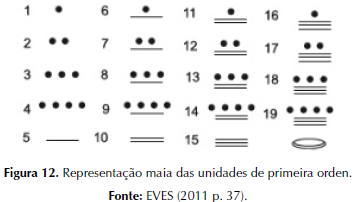
Note que sua estrutura já apresentava um símbo­lo para a quantidade zero no canto inferior direito da Figura 12.

E, para que cada algarismo ficasse em sua posição no caso em que as unidades de uma determinada ordem viesse a faltar, os sábios maias inventaram o zero. Conceito ao qual foi atribuída, por razões que hoje nos escapam, uma forma bastante semelhante a uma concha ou uma casinha de caracol. (IFRAH, 2010, p. 253)

Há uma peculiaridade nesse sistema diferente­mente dos demais povos. Os maias não representa­vam suas quantidades na horizontal e sim na vertical. As quantidades da primeira ordem eram formadas pelas próprias unidades representadas por pontos ou traços. Já as quantidades da segunda ordem eram multiplicados por 20. O problema desse sistema de numeração fica evidente a partir da terceira ordem, pois as quantidades nessa ordem eram multiplicados 360 e não por potências de base 20, neste caso, por 400. O valor ‘360’ era oriundo da multiplicação de 20 por 18, segundo EVES (2011), pelo fato do ano maia possuir 360 dias. Na quarta ordem os núme­ros eram multiplicados por 7 200 (360 x 20 ou 18 x 202), quinta ordem 144 000 (7 200 x 20 ou 18 x 203) e assim por diante. Acompanhe um exemplo:

O sistema de numeração dos Maias não foi dis­seminado aos povos ocidentais até as descobertas vindas da Índia. No século III a.C., os indianos já haviam criado um sistema de numeração com nove símbolos distintos e independentes um dos outros, todavia, ainda não existia a regra de posição e havia símbolos específicos para os múltiplos de 10, até 90 000. Ainda limitado, esse sistema só poderia fazer registros até 99 999, o que provavelmente levou os hindus no século IV d.C., a criarem novos métodos, como o registro por extenso (IFRAH, 2010). É percep­tível que os hindus estavam ‘abrindo portas’, para o sistema de numeração decimal, que utilizamos hoje.

A partir de meados do século IV d.C. os números passaram a ser representados em ordem contrária do que costumamos utilizar, ou seja, o que escrevemos hoje como ‘seis mil setecentos e vinte e cinco’, os hindus escreviam algo como ‘vinte e cinco sete­centos e seis mil’.

Um século mais tarde, os hindus deram início a um sistema de numeração oral de posição, quando excluíram da escrita por extenso qualquer menção para dez e suas respectivas potências. Assim, o exemplo do parágrafo anterior passou a ser escrito como ‘cinco dois sete seis’. Os empecilhos conti­nuavam a aparecer, já que o zero ainda não existia nessa cultura e as grafias variavam de acordo com quem os registrava.

É evidente a importância da poesia na cultura dos hindus, principalmente quando os mesmos pas­saram a utilizar diversas palavras como sinônimo dos números. Assim, os números poderiam ser re­presentados de diferentes maneiras, o número um, por exemplo, poderia ser escrito como ‘o corpo’ ou o número dois como ‘os gêmeos’ (IFRAH, 2010).

Por volta do século VII d.C., os hindus já domina­vam as técnicas do cálculo, e para tanto fizeram uso de uma espécie de ábaco de areia no qual os algarismos poderiam ser registrados, desse modo, a quantidade que representava o nada (zero) era registrada por um espaço vazio (IFRAH, 2010). Nessa época, observa­mos uma valorização dos algarismos hindus, o que significou um grande avanço, sobretudo na superação de técnicas de cálculo com fichas e pedras.

Ainda no mesmo século, o ábaco de areia foi substituído pelo sistema posicional como conhe­cemos hoje e o ‘vazio’ passou a ser representado por um círculo.

Nesse mesmo período os árabes conheceram as descobertas dos hindus e, podemos definir esse como o início da propagação desse sistema de nu­meração, bem como das técnicas do cálculo. Nessa etapa, destacamos a importância da contribuição de culturas diferentes para o desenvolvimento ou disseminação dos conhecimentos construídos du­rante as gerações anteriores. É bem provável que se os árabes não tivessem estabelecido relações comerciais com os hindus, tais inovações demo­rassem muito mais para chegar aos demais povos (Figura 13).

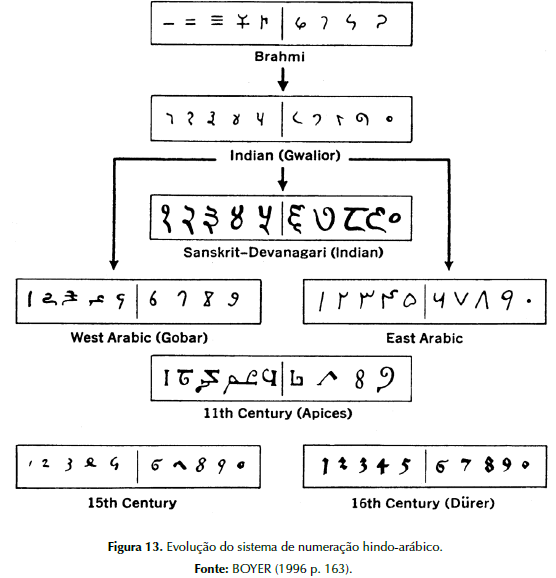
Foram séculos até que as conquistas dos hindus se difundissem por toda a Europa, já que o sistema de numeração era bem mais prático que os vigen­tes até então. Para isso merece destaque Gerbert d’Aurillac, que contribuiu para que os algarismos romanos (que até então prevaleciam) deixassem de ser vistos como uma verdade absoluta e universal (IFRAH, 2010). Afinal, o sistema de numeração cria­do pelos hindus, além de mais prático, contribuiu para o desenvolvimento de outras áreas como, por exemplo, da Álgebra.

No século X d.C., os números modernos gan­ham mais visibilidade em toda a Europa, por sua eficácia, sobretudo com a padronização das grafias árabes que foram divulgadas pela imprensa no ano de 1440. Com a Revolução Francesa, ficou eviden­te a importância desse sistema de numeração, um sistema decimal posicional, criado pelos hindus e divulgado pelos árabes.

4. Consideraçs Finais

O estudo epistêmico possibilita análises crítico-re­flexivas dos elementos envolvidos em uma recons­trução histórica do conhecimento, em nosso caso do conhecimento matemático e, mais especificamente, dos sistemas de numeração.

Não há ‘um’ inventor do sistema de numeração decimal, mas uma coletividade que mesmo com passos lentos, em diferentes épocas e lugares, de­ram ricas contribuições ao sistema de numeração que aprendemos e usamos com tanta praticidade no dia a dia. Foram necessários séculos até que o sistema de numeração decimal, hoje adotado por grande parte das sociedades hodiernas, fosse criado, desenvolvido, adaptado e formalizado.

Essa pesquisa nos possibilitou evidenciar que di­ferentes culturas, em um mesmo período de tempo, desenvolveram sistemas de numeração posicionais (Babilônios, Maias e Indianos) e não posicionais (Egípcios, Chinês, Gregos, Romanos). Alguns cria­ram um símbolo que representava a quantidade zero (Babilônios, Maias e Indianos), outros ignoraram completamente essa quantidade.

Ao encontro deste paradigma, observamos a importância da representação da quantidade zero para que seja possível a existência de um sistema de numeração posicional. Nesse sentido notamos que algumas civilizações que desenvolveram um sistema de numeração posicional compreenderam esse conceito e criaram um símbolo para represen­tar o ‘nada’.

É possível notar também, que todos os sistemas de numeração antigos, estudados nesta pesquisa, utilizaram o princípio aditivo. Já o princípio multi­plicativo esteve presente nos sistemas babilônico, maia, chinês e indiano.

As civilizações desenvolveram sistemas com di­ferentes bases numéricas, os babilônios utilizaram a base 60, enquanto que os maias utilizaram a base 20. Algumas civilizações como os gregos e os ro­manos, usaram a base 10, buscando símbolos auxi­liares, além de utilizarem princípios que tornavam ainda mais complexos seus sistemas.

Percebemos que a existência de diferentes bases não modificou a eficácia dos sistemas posicionais, no entanto a base dez prevaleceu entre todas tor­nando-se a mais usual hodiernamente, porém com uma estrutura bem mais sofisticada e eficiente.

No que tange ao traçado dos símbolos, todos sofreram alteração no decorrer do tempo, principal­mente pelo fato de os registros serem manuscritos até o século XV d.C., quando foi criada a imprensa. Sinteticamente, resumimos a estrutura dos sis­temas de numeração analisados nesse trabalho no Quadro 2.

O sistema de numeração posicional hindu-ará­bico prevaleceu e prevalece até o século XXI da nossa era. Mas, refletindo sobre a reconstrução dos sistemas de numeração empreendida neste artigo, cabe a pergunta: serão desenvolvidos outros siste­mas de numeração que superem a eficiência do sistema atual?

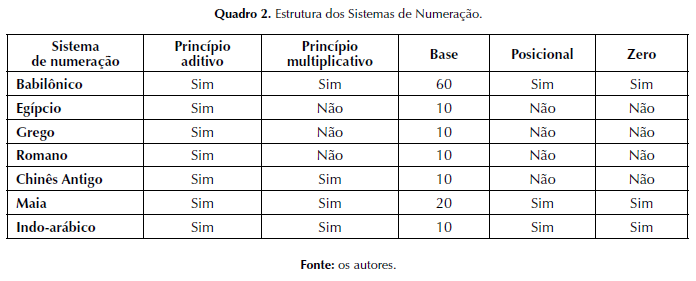
A abordagem Histórico-Epistemológica utilizada neste trabalho para empreender uma reconstrução dos sistemas de numeração, em diferentes cultu­ras, possibilitou-nos, assim como evidenciado por LUCCAS (2004), uma ampliação de nossa visão sobre o sistema de numeração que utilizamos, ofe­recendo-nos um enriquecimento conceitual que pode ser estendido a escolas e universidades por meio de propostas pedagógicas intencionalmente elaboradas e conduzidas.

Nesse sentido, esperamos que esse trabalho possa contribuir com o Ensino de Matemática, segundo a síntese Histórico-Epistemológica empreendida, uma vez que a mesma poderá servir de aporte conceitual para intervenções pedagógicas diversas.

Notas de Rodapé

1 . Segundo ALMEIDA (2009), o Osso de Ishango encontra-se atualmente no Museu de História Natural de Bruxelas.

2 . O princípio aditivo caracteriza-se pela adição dos valores individuais de símbolos resultando em outro valor.

3 . O principio multiplicativo caracteriza-se pelo produto de cada algarismo pelo valor de sua posição em um número.

5. Referências Bibliográficas

ALMEIDA, M.C. Origens da Matemática: a pré-his­tória da matemática. (Vol 1). Editora Progressiva. Curitiba: Brasil. 2009.

ANDRÉ, M. O que é um estudo de caso qualitativo em educação? Revista da FAEEBA – Educação e Contemporaneidade, Salvador, v. 22, n. 40, pp. 95-103. 2013.

ARAMAN, E.M.O. Contribuições da história da matemática para a construção dos saberes do professor de matemática. 228p. Programa de Pós-Graduação em Ensino de Ciências e Edu­cação Matemática, Doutorado em Ensino de Ciências e Educação Matemática, Universidade Estadual de Londrina, Londrina, PR, Brasil, 2011. Disponível em : <http://www.bibliotecadigital.uel.br/document/?code=vtls000168190>, Visitado em 15 abr. 2019.

ASTOLFI, J.P.; DEVELAY, M. A Didática das Ciências. Papirus. Campinas, SP: Brasil. 1995.

BARONI, R.; NOBRE, S.A pesquisa em história da matemática e suas relações com a Educação Matemática. In: BICUDO, M.A.V. (Org.). Pes­quisa em Educação Matemática: concepções e perspectivas. UNESP. São Paulo: Brasil. 1999. pp. 129-149.

BOYER, C.B. História da Matemática. 2a. ed. Trad. GOMIDE, E.F. Blücher. São Paulo: Brasil. 1996.

BRASIL. Secretaria de Educação Fundamental. Pa­râmetros Curriculares Nacionais. Matemática. Brasília: Brasil. 1997.

BRASIL. Secretaria de Estado da Educação do Para­ná. Diretrizes Curriculares da Educação Básica Matemática. Paraná: Brasil. 2008.

EVES, H. Introdução à História da Matemática. 5a. ed. Trad. DOMINGUES, H.H. Editora da UNI­CAMP. Campinas: Brasil. 2011.

GIL, A.C. Como elaborar projetos de pesquisa. 5a. ed. Atlas. São Paulo: Brasil. 2010. GODOY, A.S. Introdução à pesquisa qualitativa e suas possibilidades. Revista de Administração de Empresas, São Paulo, v. 35, n. 2, pp. 57-63. 1995.

IFRAH, G. História Universal dos Algarismos: a inteligência dos homens contada pelos núme­ros e pelo cálculo. Vol. 1. Trad. MUÑOZ, A.; KATINSKY, A.B. Nova Fronteira. Rio de Janeiro: Brasil. 1997.

IFRAH, G. Os números: a história de uma grande invenção. Globo. São Paulo: Brasil. 2010.

LUCAS, L. B. Contribuições axiológicas e episte­mológicas ao ensino da teoria da evolução de Darwin. 206p. Programa de Pós-Graduação em Ensino de Ciências e Educação Matemática, Mestrado em Ensino de Ciências e Educação Matemática, Universidade Estadual de Lon­drina, Londrina, PR, Brasil, 2010. Disponível em : < http://www.bibliotecadigital.uel.br/document/?code=vtls000154961> Visitado em 15 abr. 2019.

LUCCAS, S. Abordagem histórico-filosófica na educação matemática: apresentação de uma proposta pedagógica. 222p. Programa de Pós­-Graduação em Ensino de Ciências e Edu­cação Matemática, Mestrado em Ensino de Ciências e Educação Matemática, Univer­sidade Estadual de Londrina, Londrina, PR, Brasil, 2004.

MARTINS, A.F. História e Filosofia da Ciência no En-sino: há muitas pedras nesse caminho. Caderno Brasileiro de Ensino de Física. Santa Catarina, v. 24, n. 1, pp. 112-131, 2007.

MATTHEWS, M. História, Filosofia e ensino de Ci­ências: a tendência atual de reaproximação. Caderno Catarinense de Ensino de Física. Flo­rianópolis, v. 12, n. 3, pp. 164-214. 1995.

MIGUEL, A. Três estudos sobre História e Educação Matemática. 274p. Doutorado em Educação. Faculdade de Educação, Universidade Estadu­al de Campinas, Campinas, SP, Brasil, 1993. Disponível em: < http://repositorio.unicamp.br/jspui/handle/REPOSIP/253114 >, visitado em 15 abr. 2019.

MIGUEL, A., MIORIM, M. Â. História na Educação Matemática: propostas e desafios. Autêntica. Belo Horizonte: Brasil. 2011.

PATERLINI, R.R. Aritmética dos números inteiros. Departamento de Matemática UFSCar. São Car-los: Brasil. 2008.

ROQUE, T. História da Matemática: uma visão crí­tica, desfazendo mitos e lendas. Zahar. Rio de Janeiro: Brasil. 2012.

WALDOMIRO, T.C. Abordagem Histórico-Epistemo­lógica no Ensino da Geometria fazendo uso da Geometria Dinâmica. 90p. Dissertação (Mestrado) Programa de Pós-Graduação em Educação. Facul­dade de Educação. Universidade de São Paulo, SP, Brasil, 2011. Disponível em: < http://www.teses.usp.br/teses/disponiveis/48/48134/tde-04072011­145346/pt-br.php >. Visitado em: 15 abr 2019.