DOI:
https://doi.org/10.14483/jour.gdla.2014.2.a05Published:
2014-07-01Enseñando adición y sustracción a partir del método para el aprendizaje natural de las matemáticas y la granja de Don Juan
Teaching addition and subtraction based on the natural method of learning mathematics and farm Don Juan
Adição e subtração do ensino baseado no método natural de aprendizagem da matemática e da fazenda Don Juan
Keywords:
aggregation, difference, mathematics, grouping, sommw, soustraction, teaching (en).Keywords:
agregación, agrupación, diferencia, enseñanza, matemáticas, resta, suma (es).Keywords:
agregação, agrupamento, diferença, ensino, matemática, subtração, adição (pt).Downloads
References
Castro, E., Castro, E. (2001). Didáctica de la matemática en la educación primaria. España: Sistesis.
Díez, C., Pantano, O., Camargo, S. (2012). El desarrollo del pensamiento matemático en la primera infancia. Método para el aprendizaje natural de las matemáticas. Bogotá: Fundación para el Desarrollo Educativo y Pedagógico.
Cid, E., Godino, J. y Batanero, C. (2002). Sistemas numéricos y su didáctica para maestros. España: Editorial Universidad de Granada.
Guerrero, F., Sánchez, N. y Lurduy, O. (2006). La práctica docente a partir del modelo Deca y la teoría de situaciones. En Memorias V Festival Internacional de Matemáticas, Costa Rica, 29 al 31 de marzo.
How to Cite
APA
ACM
ACS
ABNT
Chicago
Harvard
IEEE
MLA
Turabian
Vancouver
Download Citation
doi:10.14483/jour.gdla.2014.2.a5
Resultado de investigación
ENSEÑANDO ADICIÓN Y SUSTRACCIÓN A PARTIR DEL MÉTODO PARA EL APRENDIZAJE NATURAL DE LAS MATEMÁTICAS Y LA GRANJA DE DON JUAN
Teaching addition and subtraction based on the natural method of learning mathematics and farm Don Juan
Leidy Viviana Pantano Mogollón1
1Universidad Distrital Francisco José de Caldas. Contacto: lvpmogollon@gmail.com
Recibido: 20 de junio de 2014 / Aceptado: 22 diciembre de 2014
Para citar este artículo: Pantano, L.V. (2014). Enseñando adición y sustracción a partir del método para el aprendizaje natural de las matemáticas y la granja de Don Juan. Góndola, Enseñ Aprend Cienc, 9(2), 60-78. doi: 10.14483/jour.gdla.2014.2.a05
RESUMEN
Se describen los resultados obtenidos en una experiencia en el aula, la cual se realiza a lo largo de la asignatura Práctica Intermedia V de la Licenciatura en Educación Básica con énfasis en Matemáticas de la Universidad Distrital. En dicha práctica se pretendió enseñar la noción de adición y sustracción a un grupo de estudiantes de grado primero, a partir del diseño, gestión y evaluación de una secuencia didáctica, la cual fue establecida utilizando como referente el Método para el Aprendizaje Natural de las Matemáticas y las orientaciones para el diseño y elaboración de actividades de aprendizaje y de evaluación. Los resultados más relevantes al terminar dicha práctica refieren a las estrategias a las que acudieron los estudiantes para darle solución a situaciones problema como: las estrategias sistemáticas de asignación y de conteo para así reconocer grupos con mayor o igual cantidad de objetos y para agrupar los objetos teniendo en cuenta la cantidad de elementos que debe agrupar (base); y al realizar adiciones o sustracciones tienen en cuenta el signo, además que se debe comenzar a agrupar y desagrupar desde las unidades.
Palabras Claves: agregación, agrupación, diferencia, enseñanza, matemáticas, resta, suma.
ABSTRACT
This article describes results obtained in a classroom experience that is performed at the time of the subject see intermediate practice V of the Bachelor's degree in elementary education with emphasis in Mathematics from the University District. In this practice was intended to teach the notion of addition and subtraction to a group of students from first grade, on the basis of the design, management and evaluation of a didactic sequence, which was established as a benchmark using the method for the Natural learning of mathematics and the guidelines for the design and development of learning activities and assessment. The most relevant results at the end of the practice refer to the strategies which was attended by the students to give solution to problem situations such as: the systematic strategies for allocation and counting in order to recognize groups with greater than or equal amount of objects and to group the objects taking into account the amount of elements that should be grouped together (base), and to make additions or subtractions have in account the sign, in addition they should start to group and ungroup from the drives.
Keywords: aggregation, difference, mathematics, grouping, somme, soustraction, teaching
Introducción
El artículo describe la comprensión adquirida de la noción de adición y sustracción en un grupo de 27 estudiantes de grado primero de la básica primaria en un colegio distrital de Bogotá. Se pretende trabajar la adición y sustracción a partir del Método para el Aprendizaje Natural de las Matemáticas, que consiste en una ¨propuesta de innovación que replica el orden del proceso histórico de desarrollo del pensamiento del ser humano, permitiendo el establecimiento de procesos y estadios por los cuales los estudiantes atraviesan para construir los objetos matemáticos¨ (Diez y Pantano, 2012, p. 883). Además, el método ¨pretende mejorar las formas de desarrollo del pensamiento matemático, promoviendo una buena actitud de los niños hacia este proceso y fomentando la construcción de bases y aprendizajes sólidos para afrontar los aprendizajes superiores¨ (Dez y Pantano, 2012, p. 884). Con este propósito se utiliza una metodología mediada por el diseño, gestión y evaluación de una secuencia didáctica, abordada a partir de la construcción de una situación de la que se derivan diferentes situaciones para trabajar en cada actividad de acuerdo al concepto a desarrollar.
Trabajando en la granja de Don Juan
Los estudiantes de primero trabajan en una granja, en ella deben cumplir ciertas labores que van a ser asignadas por Don Juan (el dueño de la granja): como recolectar y agrupar las diferentes verduras o frutas, para que Don Juan pueda ir a venderlas a la plaza, cuidar los animales entre otras actividades. ¡T! Tendrás que realizar estas labores, para lo cual te plantearemos una serie de actividades en el transcurso de las clases.
Desarrollo
Iniciación e introducción: sirven para que el estudiantado explicite y exteriorice sus ideas previas sobre los contenidos que se van a tratar en la unidad didáctica y compruebe la necesidad de trabajar dichos contenidos; es por ello que se realiza una actividad diagnóstico a fin de reconocer los pre conceptos sobre los contextos del nmero, con el propósito de arrojar los resultados para determinar un punto de partida en la secuencia didáctica.
Desarrollo y reestructuración: sirven para tomar contacto, asimilar y practicar los nuevos contenidos, comparar con los conocimientos anteriores, comprobar sus ventajas e incorporarlos a su experiencia personal. La forma en que se estructuró esta fase fue a través de dos actividades en las que se trabajaron nuevos contenidos, como asignación, agrupación (posicional y no posicional), agregación y diferencia.
Profundización y aplicación: son tiles para aplicar a otras situaciones los nuevos conocimientos adquiridos, reflexionar sobre las características esenciales de dichos contenidos y ampliar el conocimiento conseguido, a fin de trabajar nuevas situaciones y contextos. Es por ello que se realiza una actividad donde se trabajan los temas anteriores a partir de diferentes situaciones con el propósito de evaluar el proceso, avance y comprensión frente a los temas trabajados durante las sesiones anteriores.
Actividades de evaluación: pretenden revisar el proceso en su conjunto, es decir, valorar la efectividad del trabajo en el aula, así como la pertinencia de la secuencia didáctica y el logro de los objetivos; razón por la cual se realiza una evaluación en la que se pretende evidenciar el proceso, avance, conocer el grado de aprendizaje de los estudiantes, detectar dificultades y así reforzar los aprendizajes.
Con el propósito de desarrollar las actividades se indagaron diferentes referentes teóricos; entre estos a Diez, Pantano & Camargo (2012) quienes afirman que ¨el método para el aprendizaje natural de las matemáticas modela el desarrollo del pensamiento matemático como una sucesión de procesos cognitivos, que replican la evolución que dicho pensamiento ha tenido a lo largo de la historia de la humanidad¨ (p. 15). A partir de lo anterior construyeron, para el pensamiento numérico, unos procesos cognitivos que se definen en la Figura 1.
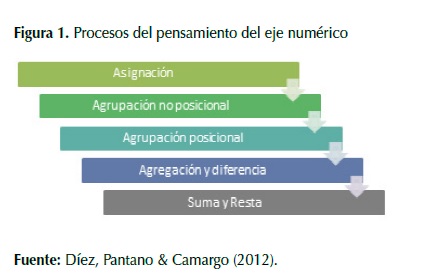
Conteo por asignación: consiste en establecer una relación biunívoca entre el elemento que se cuenta y un signo que puede establecerse segn la etapa de desarrollo de los niños.
Conteo por agrupación no posicional: nace como una necesidad de usar menor cantidad de símbolos cuando se tienen que hacer asignaciones con cantidades más grandes. De este modo, la agrupación consiste en formar grupos con el mismo nmero de elementos u objetos y a cada uno de estos grupos asignar un mismo símbolo.
Conteo por agrupación posicional: Como una necesidad derivada del proceso de agrupación no posicional, manifestada en el hecho de usar menos símbolos para representar cantidades cada vez mayores, se da lugar a la agrupación posicional. En este tipo de agrupación, un símbolo no vale por su forma o tamaño, sino por la posición relativa que ocupa con respecto a los demás elementos, así que dos símbolos de la misma forma o tamaño pueden valer cantidades diferentes si se encuentran ubicados en posiciones diferentes (Castro y Castro, 2001). Para realizar el conteo por agrupación posicional, es necesario utilizar una tabla de conteo con el nmero de columnas que se seleccionen, dependiendo de la cantidad que se va a contar y de la base seleccionada.
Agregación: nace de la necesidad de no tener que re-contar cantidades. Es decir, si se tienen dos cantidades ya contadas y se quiere conocer cuántos elementos tiene la cantidad que rene las dos cantidades conocidas, quedan dos alternativas: volver a contar todos los elementos juntos o hacer una agregación; este último recurso es más eficiente.
Diferencia: se realiza sobre cantidades, requiere que se aplique la reversibilidad de los pasos realizados para la agregación; por eso, también está conformado de dos pasos: 1. Revisar si la primera cantidad es mayor o igual al nmero de elementos de la segunda cantidad, si no es así, se requiere desagrupar un elemento de la primera cantidad de la casilla inmediatamente superior. 2. Se establece la diferencia entre las dos cantidades en cada casilla de conteo.
Suma: el proceso de la suma se realiza sobre nmeros, es decir, no están explícitas las cantidades a las que aluden las cifras numéricas; sin embargo, al haber hecho todo el proceso previo con cantidades, la mente de quien realiza la suma puede establecer nexos que le permiten ganar comprensión de este proceso abstracto. Iniciar este proceso retomando agregaciones en base diez para realizar lectura, escritura de nmeros y representación de las cantidades es necesario para enlazar este nuevo proceso con los anteriores. Con esta intención se trabaja en la tabla de agregaciones en representación gráfica y abstracta.
Resta: también es un proceso que se realiza sobre nmeros y, en ella, así como en relación diferenciaagregación, se hace uso de la reversibilidad de los pasos de la suma. Para ello se trabaja en la tabla de diferencia en representación gráfica y abstracta.
Resultados y análisis
Para dar cuenta de los resultados se tendrán en cuenta las fortalezas, dificultades que presentaron los estudiantes al realizar cada una de las actividades (evidencias), desde la actividad diagnóstico hasta la actividad de evaluación, observando lo mencionado por diferentes autores que han trabajado sobre el nmero y sus diferentes contextos, agrupación, asignación, agregación, diferencia, suma y resta, además de ello se realiza una tabulación para determinar la cantidad de estudiantes que se encuentran en dicha dificultad o fortaleza.
Conclusiones
En el transcurso de la experiencia de aula se evidenció que los estudiantes hicieron uso de diferentes estrategias que le permitieron dar solución a las situaciones problema, el solo hecho de colorear y tachar con una cruz les permitía saber la cantidad de elementos que llevaban contados o saber a qué elementos u objetos ya se les había asignado un elemento concreto; también la estrategia de encerrar los elementos les permitía realizar conteo por agrupación no posicional — aunque en algunas ocasiones modificaban la base y el tamaño de la agrupación al realizar el conteo—, además el hecho de tachar para realizar el conteo y con ello encerrar dichos elementos contados teniendo en cuenta la base dada. Así se realizaron las agrupaciones o desagrupaciones necesarias debido al cambio de unidad que se presentaba y se trabajó conteo por agrupación posicional.
Además de lo anterior, trabajar el concepto de agregación les permitió a los estudiantes encontrar alternativas más eficientes para contar dos o más cantidades y comprender que la práctica de la agregación solo se hace entre cantidades de la misma naturaleza, evitando así falsos contextos de uso de la agregación y posteriormente de la suma. Al trabajar el concepto de diferencia se evidenció que los estudiantes lograron comprender que se deben tener en cuenta los tamaños de las cantidades que se están trabajando, ya que si la primer cantidad es menor que la segunda se requiere desagrupar un elemento de la primera cantidad de la casilla inmediatamente superior y ahí sí efectuar la diferencia.
Por lo anterior se evidencia que los estudiantes le encuentran sentido y significado a los procesos y estadios por lo que atraviesan; además logran comprender a qué se refieren cuando se les menciona las frases ¨pedir prestado¨ o ¨llevo una¨, construyendo de esta manera los objetos matemáticos y mejorando así las formas de desarrollo del pensamiento matemático.
Pero esto no solo se logra con conceptos como la adición y sustracción que forman parte del pensamiento numérico, el Método para el Aprendizaje Natural también permite trabajar por medio de procesos escalonados los demás pensamientos (métrico, geométrico, variacional), que son divididos en estadios descritos por desempeños en el hacer de los estudiantes, lo cual permite una caracterización del estado de desarrollo del pensamiento matemático de una persona. Entonces queda abierta la posibilidad de trabajar con estudiantes otros conceptos de cualquier pensamiento a partir del método para así evidenciar y analizar el proceso, la construcción y la actitud de los estudiantes frente a nuevos aprendizajes, mejorando así las formas de desarrollo del pensamiento matemático a fin de afrontar los aprendizajes superiores.





Referencias bibliográficas
Castro, E., Castro, E. (2001). Didáctica de la matemática en la educación primaria. España: Sistesis.
Díez, C., Pantano, O., Camargo, S. (2012). El desarrollo del pensamiento matemático en la primera infancia. Método para el aprendizaje natural de las matemáticas. Bogotá: Fundación para el Desarrollo Educativo y Pedagógico.
Cid, E., Godino, J. y Batanero, C. (2002). Sistemas numéricos y su didáctica para maestros. España: Editorial Universidad de Granada.
Guerrero, F., Sánchez, N. y Lurduy, O. (2006). La práctica docente a partir del modelo Deca y la teoría de situaciones. En Memorias V Festival Internacional de Matemáticas, Costa Rica, 29 al 31 de marzo.
License
Gondola, Ens Aprend Cienc. is an open-access publication, free of charge for authors and readers. The publication, consultation or download of the contents of the magazine does not generate any cost for the authors or the readers, since the Francisco José de Caldas District University assumes the expenses related to edition, management and publication. The peer evaluators do not receive any economic retribution for their valuable contribution. The work of all the actors mentioned above is understood as a contribution to the strengthening and growth of the research community in the field of Science Education.
As of December 1, 2018 the contents of the journal are published under the terms of the Creative Commons License Attribution-Noncommercial- ShareAlike 4.0 International (CC-BY-NC-SA 4.0), under which others may distribute, remix, retouch, and create from the work in a non-commercial way, give credit and license their new creations under the same conditions.
The copyright holders are the authors and the journal Gondola, Ens Aprend Cienc. The holders retain all rights without restrictions, respecting the terms of the license in terms of consultation, downloading and distribution of the material.
When the work or any of its elements is in the public domain according to the applicable law in force, this situation will not be affected by the license.
Likewise, we encourage authors to deposit their contributions in other institutional and thematic repositories, with the certainty that culture and knowledge is a good of all and for all.









.jpg)




















