DOI:
https://doi.org/10.14483/23464712.14853Publicado:
2020-05-01Adição de monômios na perspectiva da teoria das situações didáticas
The addition of monomios in the prespective of the theory of didactic situations
La adición de monomios en la perspectiva de la teoría de las situaciones didácticas
Palabras clave:
teaching mathematics, algebra, didactic situations, elementary school (en).Palabras clave:
enseñanza de matemáticas, álgebra, situaciones didácticas, educación básica secundaria (es).Palabras clave:
ensino de matemática, álgebra, situações didáticas, ensino fundamental (pt).Referencias
ALMOULOUD, S. Fundamentos da Didática da Matemática. Editora da UFPR. Paraná: Brasil. 2007. https://doi.org/10.1590/S0101-32622008000100008
BARBOSA, G.S. Teoria das situações didática e suas influências na sala de aula. XII Encontro Nacional de Educação Matemática – ENEM, São Paulo. 2016. Disponível em: www.sbembrasil.org.br/enem2016/anais/pdf/7303_4383_ID.pdf. Acesso em 12 de julho de 2018.
BOGDAN, R.; BIKLEN, S. Investigação Qualitativa em Educação: uma introdução à teoria e aos métodos. Porto Editora. Porto. 2010.
BROUSSEAU, G. Introdução ao estudo da teoria das situações didáticas: conteúdos e métodos de ensino. Tradução Camila Bogéa. Ática. São Paulo: Brasil. 2008.
CHAVANTE, E.R. Convergências: matemática, 8º Ano: anos finais do Ensino Fundamental. 1ª ed. Edições SM. São Paulo: Brasil. 2015.
LUZ, G.K. de B. et al. Teoria das situações didáticas: trabalhando adição de números inteiros com o recurso do jogo. IV CONGREGO NACIONAL DE EDUCAÇÃO - CONEDU. Recife. 2017. Disponível em: <https://www.editorarealize.com.br/revistas/conedu/trabalhos/TRABALHO_EV073_MD4_SA13_ID2792_16102017213927.pdf>. Acesso em 12 de julho de 1018.
PAIS, L.C. Didática da matemática: Uma análise da influência francesa. Autêntica. Belo Horizonte: Brasil. 2001.
SILVEIRA, D.T.; CÓRDOVA, F.P. A Pesquisa Científica. In: Gerhardt, T.E.; Silveira, D.T. (Org.). Métodos de pesquisa. Universidade Aberta do Brasil - UAB/UFRGS, Curso de Graduação Tecnológica - Planejamento e Gestão para o Desenvolvimento Rural da SEAD/UFRGS. Editora da UFRGS. Porto Alegre: Brasil. 2009. pp. 31-42.
Cómo citar
APA
ACM
ACS
ABNT
Chicago
Harvard
IEEE
MLA
Turabian
Vancouver
Descargar cita
ADIÇÃO DE MONÔMIOS NA PERSPECTIVA DA TEORIA DAS SITUAÇÕES DIDÁTICAS
THE ADDITION OF MONOMIOS IN THE PERSPECTIVE OF THE THEORY OF DIDACTIC SITUATIONS
LA ADICIÓN DE MONOMIOS EN LA PERSPECTIVA DE LA TEORÍA DE LAS SITUACIONESDIDÁCTICAS
Jonas dos Santos*, Zulma Elizabete de Freitas Madruga** y Eurivalda Ribeiro dos Santos Santana***
Cómo citar este artículo: Santos, J., Madruga, Z.E.F. y Santana, E.R.S. (2020). Adição de monômios na perspectiva da teoria das situações didáticas. Gdola, ensenza y aprendizaje de las ciencias, 15(2), 339-352. DOI: http://doi.org/10.14483/23464712.14853
Recebido: 30 de abril de 2019; aprovado: 19 de julho de 2019
* Mestre em Educação Matemática, Universidade Estadual de Santa Cruz – UESC, Brasil. Correio eletrônico: jonasfisica@bol.com.br
** Doutora em Educação em Ciências e Matemática, Universidade Federal do Recôncavo da Bahia – UFRB, Brasil. Correio eletrônico:
betemadruga@ufrb.edu.br
*** Pós-doutora em Didática da Matemática, Universidade Estadual de Santa Cruz – UESC, Brasil. Correio eletrônico: eurivalda@uesc.br
Resumo
Este artigo apresenta uma pesquisa que teve como objetivo analisar as possíveis contribuições da Teoria das Situações Didáticas para a construção do conceito de adição de monômios por estudantes do 8º ano do Ensino Fundamental. A escola onde foi aplicada a intervenção faz parte da rede municipal de uma cidade, localizada na região cacaueira do sul da Bahia, Brasil. A situação didática se deu por meio de um problema no qual os estudantes teriam que extrair os monômios e efetuar a adição com o objetivo de encontrar a representação do lucro de vendas. Esses estudantes foram divididos em quatro grupos com quatro integrantes. Durante o desenvolvimento foram observadas as motivações e inquietações dos estudantes para solucionar o problema. Assim como os obstáculos epistemológicos e as dificuldades enfrentadas por eles para expressarem com clareza as etapas do desenvolvimento da situação. A Teoria das Situações Didáticas foi o aporte teórico para a construção e aplicação da situação e os resultados foram analisados de forma qualitativa. Como resultado, observou-se que a situação didática motivou os estudantes a questionarem e buscar estratégias para conseguirem construir o conceito de adição de monômios.
Palavras-chave: ensino de matemática; álgebra; situações didáticas; ensino fundamental.
Abstract
The objective of this study was to analyze the possible contributions of the theory of didactic situations to the construction of the concept of addition of monomials by eight grade students. The school where the intervention was applied is part of the municipal network of a city located in the cacao region of southern Bahia, Brazil. The didactic situation was presented as a scenario in which students were asked to extract monomials and add them with the purpose of finding the representation of the profit of sales. The students were divided into groups of four. During development, they were motivated and anxious to solve the problem. However, they experienced epistemological obstacles and difficulties in clearly identifying the stages of the development of the situation. The theory of didactic situations provided theoretical contribution to the construction and application of the situation and the results were analyzed using the qualitative method. The results revealed that the didactic situation motivated students to question and seek strategies to succeed in building the concept of monomial addition.
Keywords: teaching mathematics; algebra; didactic situations; elementary school.
Resumen
Este artículo presenta una investigación que tuvo como objetivo analizar las posibles contribuciones de la teoría de las situaciones didácticas para la construcción del concepto de adición de monomios por estudiantes de grado octavo en la secundaria. La escuela donde se aplicó la intervención forma parte de la red municipal de una ciudad, ubicada en la región cacaotera del sur de Bahía, Brasil. La situación didáctica se dio por medio de un problema en el cual los estudiantes tendrían que extraer los monomios y efectuar la adición con el objetivo de encontrar la representación del lucro de ventas. Estos estudiantes fueron divididos en grupos con cuatro integrantes cada uno. Durante el desarrollo se observaron las motivaciones e inquietudes de los estudiantes para darle solución a lo planteado; así como los obstáculos epistemológicos y las dificultades enfrentadas por ellos para expresar con claridad las etapas del desarrollo de la situación. La teoría de las situaciones didácticas fue el aporte teórico para la construcción y aplicación de la situación y los resultados fueron analizados de forma cualitativa. Como resultado, se observó que la situación didáctica motivó a los estudiantes a cuestionar y buscar estrategias para lograr construir el concepto de adici de monomios.
Palabras clave: enseñanza de matemáticas; álgebra; situaciones didácticas; educación basica secundaria.
Introdução
O processo de escolarização procura fomentar a aquisição do conhecimento pelo estudante nas diversas áreas do saber. Espera-se que durante esse processo os estudantes adquiram conhecimentos sociais, culturais e científicos, acumulados pela humanidade por milhões de anos e, as principais descobertas científicas e tecnológicas da atualidade.
Entende-se que estes conhecimentos são essenciais para a formação e emancipação do homem nos aspectos social, afetivo e cognitivo. Por meio do processo de escolarização, o indivíduo adquire habilidades, e passa a ter uma visão crítica da sociedade na qual está inserido, adquirindo capacidade de propor sugestões e modificá–las para transformar a realidade, melhorando sua qualidade de vida. Para isso, a escola precisa proporcionar-lhes condições para sua emancipação intelectual, assegurando-lhes elementos que fomentem a busca pelo saber e pela produção de novos conhecimentos.
No entanto, existe uma crítica social sobre a es-cola, pois, na maioria das vezes, ela não consegue cumprir a sua função de escolarização, quando isso acontece, os estudantes não conseguem aprender ou se interessar pelos conteúdos ensinados pelos professores. Devido a essa falta deixada pela escola na vida de alguns daqueles que passam pelo seu espaço, muitos especialistas questionam qual deve ser a real função da escola, quais tipos de conteúdos precisam ser ensinados, qual a relevância desses conteúdos na vida dos alunos, e porque o conteúdo A ou B ainda é ensinado, já que alguns conteúdos não têm um impacto direto na vida social e cultural do estudante.
A partir desses questionamentos sugiram e ainda surgem diferentes estudos, tendências e ferramentas pedagógicas com o objetivo de auxiliar e facilitar a compreensão dos conteúdos pelos estudantes, contextualizando-os com situações da vivência desses estudantes, na busca por tornar o ensino provido de significado.
Nesse cenário, a matemática aparece como a disciplina que mais assusta os estudantes, os pais e a sociedade em geral. Ela muitas das vezes é considerada como a disciplina dos gênios, a disciplina de um grupo seleto (que já nasceu com predisposição para aprender matemática), isso porque, aqueles que tiram as melhores notas na disciplina são considerados os mais inteligentes uma vez que a humanidade que cria seleções e padrões em nossa sociedade nos quais as pessoas que não se adapta normas são “excluídas” ou “deixadas para trás”.
Examinando este ponto de vista, observa-se que as pessoas usam a matemática com uma função de segregação intelectual, enaltecendo aqueles que conseguem se “dar bem” nas provas e atividades propostas e; “marginalizando”, “excluindo” aqueles ditos “não gênios”, ou “normais”. Estes acabam por acreditar no mito de que a matemática é para poucos e não conseguem aprender o conteúdo. Frequentemente preferem não participar das discussões propostas pelos professores, acreditando que é necessário apreender apenas o básico. Como consequência dessa visão equivocada, passam a dar pouca importância à disciplina e preferem dedicar-se a outras disciplinas.
E, esse dilema aumenta quando o ensino passa da fase da aritmética para algébrica. O estudante começa a trabalhar com números e “letras” ou apenas letras, isso causa uma estranheza, ele começa a questionar o porquê das letras e, quanto mais o ensino da matemática vai ficando mais “carregado de partes algébricas”, os estudantes vão se interessando menos pelo conteúdo. Porque este o assusta, aumentam-se os questionamentos sobre o porquê das letras. E parece aumentar também a distância entre os estudantes e a matemática.
Para dirimir esse impacto e levar estudantes a desenvolverem o gosto pelo conteúdo matemático, em especial pela parte algébrica, foi proposta uma situação didática em forma de problema para estudantes do 8º ano do Ensino Fundamental. Esta situação foi fundamentada na Teoria das Situações Didáticas - TSD (Brousseau, 2008) para a construção de um cenário de investigação na sala de aula. Essa teoria trabalha com a hipótese de que o conhecimento é aprendido pelo aluno por meio de regras (mensagens). A aplicação da situação ocorreu em uma escola em um município localizado na região cacaueira, sul do Estado da Bahia, Brasil. A situação didática tinha como objetivo de analisar as possíveis contribuições da Teoria das Situações Didáticas para a construção do conceito de adição de monômios por estudantes do 8º ano do Ensino Fundamental.
A situação didática foi desenvolvida a partir de uma atividade proposta na disciplina Didática da Matemática, do curso de Licenciatura em Matemática da Universidade Estadual de Santa Cruz (UESC). O objetivo da atividade consistia em elaborar, aplicar e analisar uma situação didática construída a partir da Teoria das Situações Didática de Guy Brousseau. A situação foi desenvolvida pelo primeiro1 autor e aplicada posteriormente pelo mesmo.
1. Marco teórico: a teoria das situações didáticas
A Teoria das Situações Didáticas (TSD) é uma metodologia que pode auxiliar os professores no ensino de matemática, e foi desenvolvida pelo pesquisador francês da Universidade de Bordeaux, Guy Brousseau. Nessa teoria o conhecimento é organizado e estruturado por meio de mensagens das quais o estudante se apodera daquilo que deverá ser aprendido (Brousseau, 2008).
Segundo o autor, por meio dessas mensagens o estudante modifica-se culturalmente e adapta ou retira traços culturais da sociedade da qual pertence. Dessa forma, o ensino é constituído de dois processos, “um de aculturação e outro de adaptação independente” (Brousseau, 2008 p. 18).
Sobre o processo de aculturação e adaptação, autores como Almouloud (2007) e Pais (2001), baseados em Brousseau, inferem que aculturação é o processo de mudanças que ocorrem quando dois grupos de pessoas pertencentes a culturas diferentes interagem. Durante essa interação (contando com elementos de culturas diferentes) ocorrem mudanças nos indivíduos dos grupos, porque as pessoas de cada um dos grupos se apropriam de elementos culturais e os saberes do outro grupo. No processo educacional, aculturação acontece quando os estudantes se apropriam do conhecimento científico e cultural produzido pela humanidade ao longo dos anos, e utilizam esse conhecimento para fazer mudanças em situações do seu cotidiano. A adaptação ocorre quando um indivíduo se ajusta (adapta) de forma a harmonizar-se com o meio. Assim, o estudante, de forma natural, adapta-se com o meio e com os seus elementos para a produção de conhecimento.
Com essas informações, verifica-se que o meio tem uma função fundamental no processo de ensino e de aprendizagem, por intermédio de elementos do meio, o estudante passa pelos processos de aculturação e adaptação durante as aulas. Por isso, o meio precisa ser estruturado para que a aprendizagem ocorra, uma vez que o meio é “um sistema autônomo, antagônico ao sujeito, e é deste que convém fazer um modelo, visto como um tipo autômato” (Brousseau, 2008 p. 19). Nas Situações didáticas, o meio é determinante no processo de escolarização, ele é constituído de três elementos principais: o professor, o estudante e o conhecimento. Devido à particularidade do meio,alguns autores, como Almouloud (2007), ao traduzir os trabalhos de Brousseau, preferem usar a palavra no Francês, milieu (meio), o uso da palavra escrita na língua materna, implica a não perda do seu sentindo original e das suas particularidades.
Segundo Pais (2001), a Teoria das Situações Didáticas (TSD) é constituída pelas diferentes relações pedagógicas construídas “entre o professor, o aluno e o saber”, para o autor, estas relações têm como objetivo a produção de atividades cujo foco é o “ensino e a aprendizagem de um conteúdo específico” (Pais, 2001 p. 65).
Neste contexto, verifica-se que “estes três elementos componentes de uma situação didática constitui a parte necessária para caracterizar o espaço vivo da sala de aula” (Pais, 2001 p. 65). Porém, estes elementos por si só não são suficientes para abranger toda diversidade e complexidade do fenômeno cognitivo, para isso faz necessário incorporar aos elementos do saber do sistema didático como “objetivo, métodos, posições teóricas, recursos didáticos entre outros” (Pais, 2001 p. 65).
Na TSD o conteúdo deve ser apresentado dentro de um contexto, e deve contemplar elementos da realidade do estudante, ou seja, o conteúdo precisa ser significativo para o estudante, ao ler a situação, ele precisa sentir-se motivado, desafiado a resolvê-la. Caso contrário, o conteúdo perde sua essência, a sua função didática e pedagógica. Ainda, segundo Pais (2001) o conteúdo precisa fazer uma ligação verdadeira entre o estudante e a sua realidade. Caso contrário tornar-se-á “impossível alcançar as transformações formativas do saber científico” (Pais, 2001 p. 66), ou seja, o ensino desprovido de significado não contribuirá para a formação científica, cultural e social do estudante.
Brousseau (2008 p. 19) afirma que “um problema ou um exercício não pode ser considerado mera reformulação de um conhecimento, mas um dispositivo, um meio que responde ao sujeito, segundo algumas regras”. O conhecimento precisa ser usado como o elemento motivador, capaz de mobilizar e trazer um “desconforto” ou “desequilíbrio” ao meio, diante dessa nova realidade o estudante será estimulado adaptar-se a ela pelos processos de aculturação do conhecimento e adaptação à nova realidade que lhe foi imposta.
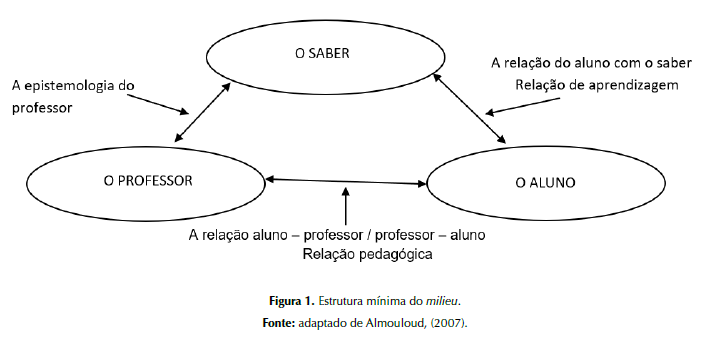
Segundo Almouloud (2007), para que as situações didáticas produzam efeitos práticos, é necessário que seja mantida a estrutura formada pelo sistema mínimo, onde deve ser mantida as interações entre professor e o estudante, intermediadas pelo saber, dentro do processo de ensino e aprendizagem. O esquema a seguir (Figura 1), adaptado de Almouloud (2007), mostra de forma resumida com ocorre essa interação.
Na teoria das situações didáticas, como já supracitado, o milieu é um fator determinante para que haja a interação entre o saber e o aluno. Nessa teoria existem três hipóteses sobre o milieu. Essas hipóteses são citadas por Almouloud (2007 p. 32):
1ª. O aluno aprende se adaptando a um milieu(meio) que é o fator de dificuldade, de descontração, de desequilíbrio, um pouco como acontece na sociedade humana;
2ª. O milieu não munido de interações didáticas é insuficiente para permitir a aquisição do conhecimento, neste caso o papel do professor é criar e organizar o milieu para serem desenvolvidas as situações suscetíveis a provocar a aprendizagem no aluno;
3ª. O milieu e as situações didáticas devem engajar fortemente os saberes matemáticos envolvidos no processo de ensino e aprendizagem.
Analisado essas hipóteses verifica-se que a motivação pela aprendizagem ocorre pela necessidade que o indivíduo tem em se adaptar às novas realidades que lhes são impostas (1ª hipótese). Para isso, o meio precisa ser munido de situações didáticas, ricas em saberes matemático e, com um fator que permita a aquisição de conhecimento pelo estudante.
Além, dessas hipóteses, existem quatro pilares associados à TSD, são elas que irão nortear as etapas de produção e aquisição do conhecimento pelo estudante. Esses pilares são: ação, formulação, validação e institucionalização, esses pilares serão sintetizados a seguir adaptado de Almouloud (2007).
Ação: Nessa fase os estudantes têm acesso ao problema proposto, procuram utilizar os conhecimentos já adquiridos para compreendê-lo e encontrar caminhos para solucioná-lo. Nesta etapa os estudantes recebem o problema, tomam conhecimento do mesmo, tentam compreender o que é pedido, começam a selecionar quais os conhecimentos lhes serão úteis, e começam a traçar estratégias para resolvê-lo, é nesse momento que as decisões são tomadas e os saberes são colocados em práticas.
Formulação: Nessa etapa, os estudantes encontram a resposta para o problema, e formulam a solução. Durante a formulação o estudante poderá se apoderar de inúmeros dispositivos para solucionar
o problema, os elementos que poderão ser utilizados poderão ser fases, esquemas, mapas mentais, elementos algébricos e representações algébricas. Esses elementos servirão de caminho para chagarem à solução do problema. Os estudantes explicarão para os colegas as estratégias e o raciocínio usados na solução.
Validação: Nessa etapa, os resultados dos estudantes são avaliados pela classe com o objetivo de verificar a existência de erros na solução proposta para o problema. Em “plenária” os estudantes começam a expor os resultados encontrados e as estratégias que foram usadas durante o desenvolvimento do problema. Nesse momento há uma discussão sobre cada solução, é verificada a validade do resultado e do método usado para se chegar à solução, ou seja, a estratégia apresentada pelos estudantes precisa ser alvo de análise do coletivo e provada dentro de um determinado contexto.
Institucionalização: O professor parte das discussões e dos resultados apresentados pelos estudantes para institucionalizar o saber matemático, ou seja, o professor faz a generalização do conhecimento e mostra para o aluno que aquele saber matemático é valido para qualquer situação e poderá ser utilizado em atividades ou outros instrumentos, para reforçar o conhecimento adquirido pelo aluno.
A partir dessa compreensão, verifica-se que a TSD poderá contribuir para que os estudantes consigam a gostar da matemática e dos seus conteúdos, uma vez que eles serão protagonistas no processo de ensino e aprendizagem, já que terão a oportunidade de propor soluções, de analisar as soluções dos colegas. Isso poderá contribuir para que este estudante venha a se aproximar da matemática, pois eles começaram a compreender o processo de construção do conhecimento matemático.
2. Metodologia da pesquisa
Esta pesquisa procurou analisar os resultados de uma situação didática para o ensino de adição de monômios, e analisar contribuições da Teoria das Situações Didáticas para a construção desse conceito por estudantes do 8º ano do Ensino Fundamental e como essa teoria poderá auxiliar o trabalho do professor como mediador entre o estudante e o conhecimento.
A pesquisa tem natureza qualitativa, pois os dados foram obtidos no ambiente da sala de aula - ambiente natural do aluno, (Bogdan, Biklen, 2010), e procura auxiliar na busca por resposta a um dilema de muitos professores sobre como fazer os estudantes gostarem de matemática.
Segundo Silveira, Córdova (2009), na pesquisa qualitativa o pesquisador visa dar uma explicação para um determinado fato sem quantificá-lo, ou seja, ao utilizar a pesquisa qualitativa o pesquisador procura “explicitar o porquê das coisas, exprimindo o que convém a ser feito, mas não quantifica valores” (Silveira, Córdova, 2009 p. 32).
Para as autoras, na pesquisa qualitativa o tamanho da amostra é irrelevante, pois o objetivo dela é a produção de novos conhecimentos/novas informações. Esse tipo de pesquisa procura elucidar um determinado fenômeno ou situação de forma clara e objetiva por meio da “hierarquização das ações de descrever, compreender e explicar” (Silveira, Córdova, 2009 p. 32) sem contaminar os dados com juízos de valores.
Os dados da pesquisa foram coletados pelo primeiro autor em duas aulas de 55 (cinquenta e cinco) minutos cada, em uma turma de 8º ano do Ensino Fundamental de uma escola pública do sul da Bahia, Brasil. Como instrumento de coleta, o pesquisador utilizou-se de diário de campo, onde registrou todas as manifestações dos estudantes no decorrer da aplicação, bem como os diálogos entre os grupos e com o professor; além de registros escritos elaborados pelos participantes da pesquisa, incluindo a resolução das questões propostas. Para a análise desses dados foram considerados as dúvidas, os questionamentos, os diálogos (registrados no diário de campo), e as soluções indicadas pelos alunos para solucionar a situação. Inicialmente o pesquisador propôs a seguinte questão:
Situação Didática: Marcos vende sovertes em potinhos, recebendo um lucro de 10% por soverte vendido. Em uma sexta-feira Marcos vendeu uma determinada quantidade de sovertes, no sábado ele vendeu o dobro do número de sorvetes vendidos na sexta-feira. Sabe-se que a cada potinho de soverte custa R$ 1,00. Então, encontre uma maneira de representar o lucro total que Marcos obteve nos dois dias de venda usando como referência o número de sorvetes vendidos na sexta (Figura 2).
Para o desenvolvimento da situação, os participantes foram divididos em grupos com quatro alunos cada, totalizando quatro grupos. O desenvolvimento da atividade em grupo teve como objetivo proporcionar a troca de conhecimento entre os estudantes e a construção coletiva do saber. A formação dos grupos foi organizada a partir das sugestões dos alunos, que escolheram com que queriam realizar a atividade. Os grupos foram denominados G1, G2, G3 e G4. A princípio cada um dos grupos recebeu
o problema, as instruções, nas quais constava que deveriam encontrar estratégias para solucionar o problema e depois expor para os colegas a solução encontrada. Em princípio os estudantes não queriam fazer as apresentações, mais acabaram aceitando posteriormente, após conversa com o professor, onde o mesmo mostrou a importância da comunicação e socialização nesse processo. Observa-se que a situação proposta pelo professor é aceita pelos estudantes, estabelecendo nesse momento o contrato didático.

Figura 2. Alunos desenvolvendo a situação2.
Fonte: dados da pesquisa.
O contrato didático segundo Brousseau (2008) é o conjunto de comportamentos que surgem da relação entre professor e aluno, ou seja, o professor espera o comportamento dos estudantes durante as aulas e estes esperam do professor, também, certos comportamentos. Esse contrato, na maioria das vezes é implícito e em outras é construído entre o professor e o estudante. No caso da situação aplicada, o contrato foi construído do diálogo entre o professor (que propôs as situações e a regras) e os estudantes (que aceitaram as condições propostas pelo professor para resolver a situação didática).
3. Resultados
Ao receber o problema os grupos procuraram solucioná-lo. No entanto, houve questionamentos e muitas dúvidas sobre como deveriam encontrar o lucro de Marcos, uma vez que o problema não traz o número de sorvetes vendidos. Isso causou um estranhamento por parte dos estudantes, porém os motivou a fazerem vários questionamentos ao professor, observando que a solução do problema não era tão óbvia, instigando-os a buscar meios alternativos para solucionar esse problema. Os grupos G1, G2 e G4 fizeram os seguintes questionamentos: “Quantos sorvetes Marcos vendeu professor?” (G1), “Professor, fala para nós o número de sorvetes vendidos na sexta e nós faremos o resto” (G2) e, “Professor, como vou fazer para encontrar o lucro de Marcos? Quais números vamos usar para fazer a conta?” (G4). Essa inquietação diante do problema proposto se refere ao que Brousseau (2008) afirma que o conhecimento precisa se um elemento motivador e trazer um “desconforto” no meio, neste caso, o problema proposto sensibilizou os estudantes que a questionar ao verificar que a forma adotada por eles para resolver problema não era suficiente para encontra a solução para o que lhes foi proposto.
O grupo G3 atribuiu os valores para o lucro das vendas de sorvetes da sexta, com o intuito de resolver o problema gerando um lucro de R$ 9,00 para Marcos. Como pode ser verificado na Figura 3.

Nesse momento, foram feitos alguns questionamentos pelo professor, aos grupos, como: “O problema está pedindo o lucro ou uma representação do lucro, será que é necessário saber quantos sorvetes foram vendidos para encontrar a solução do problema? [...], pensem um pouco, quais conhecimentos já foram vistos que nos dará suporte para resolver o problema? A situação está pedindo um número ou uma representação?” Esse estranhamento é normal na TSD, pois significa que a situação provocou os estudantes, eles foram motivados e desafiados a procurar a solução, isso configura o desequilíbrio provocado pelo problema no meio, cujo objetivo é justamente provocar uma reação de desconforto nos estudantes, que ao questionarem sobre como resolver o problema, procurarão respostas, atribuindo valores aleatórios para solucioná-lo. Verifica-se aqui uma tentativa do estudante encontrar o fator equilíbrio para o meio (solução para o problema). Após os questionamentos feitos pelo professor, os estudantes começaram a estruturar algumas estratégias e recorreram a diversas maneiras para solucionar o problema. Essa etapa na TSD corresponde ao processo da Ação.
Os grupos G1, G2 e G4, trocando informações, chegaram à conclusão que Marcos iria lucrar R$ 0,10 por cada sorvete vendido. Porém, o grupo G3 ficou questionando e afirmando que para solucionar o problema precisaria do número de sorvetes vendidos, e a situação não trazia esse valor. Mas, após o diálogo com o professor e os demais colegas dos outros grupos, chegaram à mesma conclusão de R$ 0,10 por sorvete. O grupo G4 chegou a esse valor por dedução; os grupos G1 e G2 usaram algoritmos para obter o valor (Figuras 4 e 5); e G3 fez uma representação de igualdade, não conseguindo descrever como chegaram aos R$ 0,10 por sorvete vendido (Figura 6). No entanto, o cálculo de valor unitário por sorvete vendido, motivou os grupos a encontrarem o lucro de Marcos na sexta-feira, no sábado e o lucro total.

Após esta etapa, os grupos começaram a montar as situações que deveria representar o lucro da venda de sorvete. Nesse momento os estudantes perceberam que a quantidade de sorvetes vendidos iria condicionar um lucro maior ou menor, como se pode verificar na fala de dois estudantes3: “Professor, quantos mais sorvetes vendidos, maior vai ser o que Marcos vai receber. Se ele vende 10 sorvetes svai ganhar um real, mais se vender mais ganha mais” (Aluno C do grupo G2); e “então ele tem que ralar muito para ganhar um dinheirinho bom” (Aluno J do grupo G1). Neste caso, eles teriam que multiplicar o valor unitário pela quantidade de sorvetes vendidos. Foi possível observar que a situação levou os estudantes a irem além do conteúdo proposto, pois de maneira intuitiva levou esses estudantes perceberem a noção de função. Os estudantes finalizam essa etapa propondo as devidas soluções. Essa fase na Teoria das Situações Didáticas é chamada de Formulação. Aqui os alunos formularam as possíveis representações para a situação didática.
Após a fase de formulação, o professor propôs uma plenária para que os grupos explicitassem os resultados encontrados, as dificuldades e os caminhos usados para encontrar uma representação para o lucro. O professor sugeriu aos grupos que demonstrassem seus resultados, enquanto os outros deveriam avaliar se a solução proposta serviria para demonstrar o lucro das vendas ou não. Caso não servisse, a expressão ou a solução deveria ser eliminada ou melhorada com sugestões dos grupos, pois o estudante nesse fazer irá validar as soluções encontradas. Essa etapa é chamada de Validação, conforme se pode observar a seguir.
Os grupos G4 e G2 apresentaram os seus modelos para a representação do lucro das vendas, usando uma incógnita (uma letra) a qual representaria a quantidade de sorvetes vendidos. Para isso, eles partiram da ideia de que o número de sorvetes vendidos na sexta-feira deveria ser multiplicado pelo valor unitário. O lucro do sábado corresponderia ao lucro de sexta multiplicado por dois, e após eles deduziram que deveriam somar o lucro de sexta com o lucro do sábado. O grupo G2 afirmou que não teve dificuldade em encontra a solução, G4 afirmou que tiveram dificuldades em encontrar uma forma de relacionar as vendas de sexta-feira com as vendas do sábado, para posteriormente encontrarem uma representação do lucro total, mas, depois de testarem vários valores para x chegaram a conclusão que deveriam adicionar as partes numéricas da cada expressão, encontrando também a expressão 0,30x para representar o lucro. A Figura 7 mostra a representação para o lucro da venda de sorvete do grupo G2, eles utilizaram a letra x para representar o número de sorvetes vendidos.

O grupo G3 encontrou as expressões para representar o lucro da sexta-feira e do sábado, que foram respectivamente 0,1x e 0,2x, mas segundo os estudantes, o grupo perdeu muito tempo tentando atribuir valores numéricos para determinar o lucro das vendas, e não tiveram tempo para concluir, não encontrando uma forma de relacionar as duas expressões. Porém, tinham certeza que deveriam somar essas duas expressões, só não sabiam como, suspeitavam que devessem somar os “neros que estão junto das letras” (Aluno F). A Figura 8 apresenta a solução proposta pelo grupo G2. A letra ‘S’, o grupo usou para representar o número de sorvetes vendidos na sexta-feira.

O grupo G1 apresentou seu resultado com uma solução diferente da esperada pelo professor (Fi
gura 9). O grupo encontrou a expressão para a venda de sorvetes da sexta-feira 0,10B onde B é o número de sorvetes vendidos na sexta-feira, o lucro do sábado corresponde ao dobro da venda da sexta-feira e o lucro da venda da sexta-feira e do sábado juntos corresponde ao triplo da venda de sexta-feira. A Figura 9 mostra a conclusão pro-posta pelo grupo G1.

Durante as apresentações, os estudantes foram opinando sobre cada solução apresentada. Eles concluíram que as soluções dos grupos G1, G2, G4 poderiam ser usadas para calcular o lucro das vendas, já o modelo do grupo G3, deveria ser melhorado (somar as expressões encontradas). Mais uma vez, surgiu a discussão iniciada pelos estudantes, sobre que o lucro dependerá da quantidade de produtos vendidos e se por acaso Marcos vendesse pouco, não compensaria trabalhar na venda de sorvetes. Aqui voltou a ideia de função, onde o lucro está condicionado à quantidade de sorvetes vendidos. Surgiu também uma discussão que Marcos deveria negociar com o patrão uma porcentagem maior sobre a venda dos sorvetes, pois com esse percentual ele não lucraria muito. Como supracitada, a discussão dos resultados feita pelos alunos, corresponde à etapa de Validação na TSD, uma vez que os grupos avaliaram os resultados dos outros grupos e verificaram se as soluções eram suficientes para resolver a situação.
Depois das apresentações, foi realizada a Institucionalização do conteúdo pelo professor, a partir das soluções dos alunos. O professor (pesquisador e primeiro autor deste artigo) comentou sobre os resultados dos grupos, as dificuldades encontradas pelos alunos e sobre o lucro, ou seja, reforçou as conclusões dos alunos de que o lucro estava relacionado com a quantidade de sorvetes vendidos (reafirmando de forma intuitiva a noção de função). O professor começou a discussão usando dois conceitos, explicitados a seguir:
» Marcos ganhará R$ 0,1 por sorvetes vendidos, se ele vendeu x sorvetes na sexta então o lucro será o nero de sorvetes multiplicado pelo valor unitário, então a representação do lucro nesse dia é R$ 0,1x.
» No sábado ele vendeu o dobro de sorvetes da sexta, ou seja, 2x sorvetes e a representação do lucro é R$ 0,1 multiplicado por 2x, logo a representação do lucro no sábado será R$ 0,2x.
Após as discussões entre o professor/pesquisador e os grupos, o conceito de monômios semelhantes foi deduzido pelos estudantes: dois ou mais monômios são semelhantes quando suas partes literais são iguais4. Nesse sentido, os dois monômios que foram encontrados para representar o lucro da venda de sorvetes por Marcos: 0,1x e 0,2x. Daí pode-se observar que os dois possuem a mesma parte literal, logo eles são monômios semelhantes.
Outro conceito apreendido pelos estudantes foi no que se refere à adição de monômios semelhantes: Na adição de monômios semelhantes, adicionam-se os coeficientes (parte numérica) dos monômios semelhantes e preserva-se a parte literal5. Aplicando o conceito da adição de monômios para encontrar o lucro de Marcos nos dois dias de venda, obtêm-se: 0,1x + 0,2x = (0,1+0,2)x = 0,3x. O que se pode concluir que a representação do lucro de Marcos é 0,3x.
Durante a institucionalização, o professor discutiu o resultado do grupo G1 o qual encontrou a representação do lucro usando o triplo do valor das vendas da sexta-feira, e explicou que em casos semelhantes será possível usar esse raciocínio. Mas, na maioria dos casos de adição de monômios, será necessária a utilização do conceito de adição. E ressaltou que apesar do grupo G3 não ter demonstrado uma solução por escrito, os raciocínios do grupo estavam corretos.
a. Diálogo entre resultados dessa pesquisa com os resultados de outras pesquisas6
A partir da análise dos resultados foi proposto um diálogo desta pesquisa com duas pesquisas que utilizaram a TSD como metodologia para trabalhar conceitos matemáticos em sala de aula. Para esse diálogo foram selecionados os trabalhos Barbosa (2016) e de Luz et al. (2017), por se assemelharem com o objetivo desta pesquisa. O primeiro procurou analisar como os jogos contribuem para a aprendizagem dos estudantes e como essa metodologia se relaciona com a TSD; e o segundo procurou verificar como um professor trabalha o conteúdo de raízes, funções e propriedades “à luz da teoria das Situações Didáticas que surgiram durante uma aula de Matemática” (Barbosa, 2016 p. 9).
Observa-se, no trabalho de Luz et al. (2017, p.6) que o professor iniciou a aula “por meio de uma metodologia convencional, ou seja, aula expositiva” para fazer a explanação do conteúdo, adição de neros inteiros. Após a explanação ele aplicou uma questão do tipo calcule, da qual os estudantes erraram 80% como pode ser verificado na Figura 10.

Como já foi mencionado na fundamentação teórica, na TSD o ideal é que o professor comece a aula com uma situação didática que leve os estudantes a serem protagonistas na construção do conhecimento. Isso pode ser verificado no desenvolvimento da situação proposta nesse artigo, que por meio de uma situação em forma de problema os estudantes chegaram construir o conceito de adição de monômios de forma intuitiva, algo que não aconteceu em no trabalho de Luz et al. (2017), uma vez que o professor iniciou a aula explicando o conteúdo e, aplicando a questão (Figura 10), logo após a aula dialogada.
Na TSD o professor precisa criar uma situação no qual o estudante construa um raciocínio para a aquisição e construção de conceito matemático. No entanto, verifica-se na questão usada por Luz et al. (2017), possui característica do ensino tradicional, uma vez que a questão não traz nenhum grau de dificuldade ou situação que contribua com a construção de conceitos matemáticos pelos estudantes. No ponto de vista dos autores desta pesquisa, ela serve apenas para verificar se o estudante aprendeu ou não o conteúdo, não fornecendo elementos que instiguem a criatividade do estudante.
Em um segundo momento foi trabalhado um jogo com os estudantes com objetivo de verificar se o mesmo facilitaria a aprendizagem do conteúdo. Após trabalhar o jogo, os pesquisadores apresentaram questão a mesma para os estudantes. Segundo os autores Luz et al. (2017), o jogo se tornou um facilitador de aprendizagem. No entanto, analisando as etapas da TSD, verifica-se que o interessante seria que os autores iniciassem a aula com o jogo e deixassem que os alunos fossem construindo os conceitos de adição de números inteiros durante o momento lúdico. Sobre a questão aplicada, sugere-se que a mesma deveria ser elaborada em forma de problema com objetivo dialogar com o jogo e, por meio desse diálogo, o estudante iria construindo de forma intuitiva o conceito esperado pelo professor. Da forma como o jogo foi aplicado (após a exposição do conteúdo), o mesmo funcionou como um instrumento que contribuiu para dirimir as dificuldades não sanadas na aula expositiva, como forma de reforço, ou para consolidar o conteúdo trabalhado pelo professor. Luz et al. (2017) apresentaram algo análogo a esta pesquisa, pois concluíram afirmando também que os estudantes estão mais familiarizados com as aulas de matemáticas tradicionais.
No caso do trabalho de Barbosa (2016), foi analisado uma aula de matemática procurando ressaltar “os pontos comuns, segundo a Teoria da Transposição Didática de Chevallard (1991), Teoria das Situações Didáticas e o Contrato Didático de Guy Brousseau (1986)” (Barbosa, 2016 p. 9). A pesquisa Barbosa (2016) se difere desta pesquisa e da Luz et al. (2017) uma vez que as duas últimas procuraram analisar as contribuições da TSD na construção do conhecimento pelo estudante. Examinando a pesquisa Barbosa (2016) verificou-se que o autor procurou analisar como uma aula de matemática se encaixava na TSD. Segundo Barbosa (2016) o problema apresentado em sala de aula motivou os estudantes, propondo a resposta para o problema proposto. No entanto, segundo o autor o profes-sor deu continuidade à aula, revelando o nome do conteúdo. Não socializou as respostas dos alunos e não as valorizou durante a institucionalização do conteúdo. Logo, o professor não proporcionou condições para que os estudantes desenvolvessem as fases da TSD. Segundo Barbosa (2016), caso a situação estivesse sido proposta na perspectiva da resolução de problema, poderia contribuir para as fases da TSD foi valorizadas durante o processo de resolução do problema.
Pode-se inferir que a situação didática proposta pelo professor na pesquisa de Barbosa (2016) (Figura 11), poderiam levar os estudantes a permear pelas fases da TSD, para isso seria necessário o profes-sor criar situações que motivassem os estudantes a construir, de forma intuitiva, o conceito esperado por meio do questionamento e do direcionamento dos estudantes.
Analisando a fundamentação teórica dessa pesquisa, os resultados da mesma e o diálogo com pesquisas correlatas Luz et al. (2017) e Barbosa (2016), verifica-se que na TSD o conhecimento precisa ser reformulado em forma de situação didática na qual
o estudante encontrará suporte para a construção do conhecimento de forma intuitiva, neste caso o estudante passa a ser protagonista no processo de ensino e aprendizagem. O problema não pode ser aplicado após a explicação do conteúdo como aconteceu em no trabalho de Luz et al. 2017), o professor precisa valorizar as respostas dos estudantes, instigá-los a discutir o problema, a formular hipótese, a traçar estratégias para a resolução do mesmo e demonstrar para os colegas o processo pelos quais chegaram ao resultado, discutindo porque o mesmo é válido como resolução do problema, fato que não aconteceu nos trabalhos de Luz et al. (2019) e Barbosa (2016), mas foi contemplado nesta pesquisa. A situação deve ser formulada para não apresentar equívocos, caso contrário, o estudante construirá conceitos diferentes do esperado, como ocorreu nesta pesquisa e pode ser verificada na solução do resultado apresentado por G1.
4. Considerações finais
Este artigo apresentou uma pesquisa cujo objetivo era analisar as possíveis contribuições da Teoria das Situações Didáticas para a construção do conceito de adição de monômios por estudantes do 8º ano do Ensino Fundamental.
Conforme observações do professor durante a atividade foi, possível verificar que no início os estudantes tiveram um pouco de dificuldades para compreender a situação e como deveriam resolvê-la. Começaram atribuindo valores para encontrar uma solução para o lucro das vendas de sorvetes. Pode-se inferir que essas dificuldades ocorreram porque eles não tinham o costume de trabalhar com situações desse tipo, ou seja, partindo de um cenário o qual apresentava um problema, para construir um conceito.

No entanto, apesar das dificuldades, a situação conseguiu motivar os alunos a questionarem, a perguntarem e traçarem estratégias para solucionar o problema. Com isso, constatou-se que o problema apresentado não teve grande nível de dificuldade, no momento de dedução da resposta, no entanto, havia certa dificuldade implícita, a qual motivou os estudantes na busca por respostas que pudessem explicitar para os demais colegas.
Conforme o resultado apresentado pelo grupo G1, a situação apresentou um equívoco de construção, porque se todos os grupos estivessem resolvido o problema usando o método adotado por G1 a situação didática perderia seu objetivo principal que era a adição de monômios. Porém, o professor poderia usar outro conceito de monômios que seria a multiplicação de um número real por um monômio. Os pontos fortes dessa atividade são expressos pelo fato dos grupos conseguirem encontrar a solução para a situação, sendo que três deles usaram o conceito intuitivo de adição de monômios e além disso, os estudantes conseguiram extrair do problema o conceito de função (além do conteúdo trabalhado).
Com isso, verificou-se na prática a funcionalidade da TSD, dessa forma, percebe-se que o problema precisa ser construído com o objetivo de motivar o estudante e desafiá-lo, a situação didática precisa ser construída para que reconstruir o conceito matemática esperado pelo professor, caso contrário, a situação poderá levar o estudante a construir conceitos diferentes do planejado pelo professor. Observou-se que ao desenvolver a atividade em sala de aula baseada nessa teoria o estudante é o protagonista na busca pelo saber, pois ele tem a oportunidade “construir” resultados e expô-los para seus colegas, os quais irão ajudá-lo nessa construção. Com o uso da TSD, por exemplo, o professor poderá instigar os estudantes para a construção de conceitos importantes e, também, a se interessarem pelas aulas de matemáticas.
Notas de rodapé
1 . A ênfase em citar o primeiro autor está no fato de esclarecer a metodologia, apontando a participação de um dos autores como participante da pesquisa (professor/pesquisador). No entanto, todos os autores contribuíram ativamente durante toda a pesquisa.
2 . Cabe salientar que os pais dos estudantes autorizam o uso de imagem no início de cada ano letivo. Além disso, os colaboradores concordaram em participar da pesquisa, assinando um termo de consentimento.
3 . Com o objetivo de manter o anonimato dos estudantes, os seus nomes foram substituídos por uma letra maiúscula do alfabeto sendo que foram 16 estudantes sendo nomeado de A até Q.
4 . Adaptado da página 114 do livro didático: CHAVANTE, E.R. Convergências: matemática, 8º Ano: anos finais do Ensino Fundamental. 1ª edição. Edições SM. São Paulo: Brasil. 2015.
5 . Adaptado da página 115 do livro didático: CHAVANTE, E.R. Convergências: matemática, 8º Ano: anos finais do Ensino Fundamental. 1ª edição. Edições SM. São Paulo: Brasil. 2015.
6 . Foi feito uma busca no banco de dado do Google acadêmico com o objetivo de encontra pesquisa que usaram TSD em sala de aula, foi analisado os títulos e as palavras chaves dos 50 primeiros trabalhos, e deste apenas os dois trabalhos que foram selecionados eram resultado de aplicação em sala de aula.
5. Referências bibliográficas
ALMOULOUD, S. Fundamentos da Didática da Matemática. Editora da UFPR. Paraná: Brasil. 2007. https:// doi.org/10.1590/S0101-32622008000100008
BARBOSA, G.S. Teoria das situações didática e suas influências na sala de aula. XII Encontro Nacional de Educação Matemática – ENEM, São Paulo. 2016. Disponível em: <www.sbembrasil.org.br/enem2016/anais/pdf/7303_4383_ID.pdf>. Acesso em 12 de julho de 2018.
BOGDAN, R.; BIKLEN, S. Investigação Qualitativa em Educação: uma introdução à teoria e aos métodos. Porto Editora. Porto. 2010.
BROUSSEAU, G. Introdução ao estudo da teoria das situações didáticas: conteúdos e métodos de ensino. Tradução Camila Bogéa. Ática. São Paulo: Brasil. 2008.
CHAVANTE, E.R. Convergências: matemática, 8º Ano: anos finais do Ensino Fundamental. 1ª ed. Edições SM. São Paulo: Brasil. 2015.
LUZ, G.K. de B. et al. Teoria das situações didáticas: trabalhando adição de números inteiros com o recurso do jogo. IV CONGREGO NACIONAL DE EDUCAÇÃO – CONEDU. Recife. 2017. Disponível em: <https://www.editorarealize.com.br/revistas/conedu/trabalhos/TRABALHO_EV073_MD4_SA13_ ID2792_16102017213927.pdf>. Acesso em 12 de julho de 1018.
PAIS, L.C. Didática da matemática: Uma análise da influência francesa. Autêntica. Belo Horizonte: Brasil. 2001.
SILVEIRA, D.T.; CÓRDOVA, F.P. A Pesquisa Científica. In: Gerhardt, T.E.; Silveira, D.T. (Org.). Métodos de pesquisa. Universidade Aberta do Brasil – UAB/UFRGS, Curso de Graduação Tecnológica – Planejamento e Gestão para o Desenvolvimento Rural da SEAD/ UFRGS. Editora da UFRGS. Porto Alegre: Bras
Licencia
Góndola, Ens Aprend Cienc. es una publicación de acceso abierto, sin cargos económicos para autores ni lectores. La publicación, consulta o descarga de los contenidos de la revista no genera costo alguno para los autores ni los lectores, toda vez que la Universidad Distrital Francisco José de Caldas asume los gastos relacionados con edición, gestión y publicación. Los pares evaluadores no reciben retribución económica alguna por su valiosa contribución. Se entiende el trabajo de todos los actores mencionados anteriormente como un aporte al fortalecimiento y crecimiento de la comunidad investigadora en el campo de la Enseñanza de las Ciencias.
A partir del 01 de diciembre de 2018 los contenidos de la revista se publican bajo los términos de la Licencia Creative Commons Atribución–No comercial–Compartir igual 4.0 Internacional (CC-BY-NC-SA 4.0), bajo la cual otros podrán distribuir, remezclar, retocar, y crear a partir de la obra de modo no comercial, siempre y cuando den crédito y licencien sus nuevas creaciones bajo las mismas condiciones.
Los titulares de los derechos de autor son los autores y la revista Góndola, Ens Aprend Cienc. Los titulares conservan todos los derechos sin restricciones, respetando los términos de la licencia en cuanto a la consulta, descarga y distribución del material.
Cuando la obra o alguno de sus elementos se halle en el dominio público según la ley vigente aplicable, esta situación no quedará afectada por la licencia.
Asimismo, incentivamos a los autores a depositar sus contribuciones en otros repositorios institucionales y temáticos, con la certeza de que la cultura y el conocimiento es un bien de todos y para todos.




















