DOI:
https://doi.org/10.14483/23464712.13317Publicado:
2019-01-01Funções quadráticas e tecnologías móveis: ações cooperativas em um experimento no ensino médio
Quadratic functions and mobile technologies: cooperative actions in a experiment to teaching in high school
Funciones cuadráticas y tecnologías móviles: acciones cooperativas en un experimento para la enseñanza en educación media
Palavras-chave:
Learning, Primary School, Teaching, Mathematics (en).Palavras-chave:
aprendizaje, escuela básica, educación, matemáticas (es).Palavras-chave:
aprendizagem, escola básica, ensino, matemática (pt).Downloads
Como Citar
APA
ACM
ACS
ABNT
Chicago
Harvard
IEEE
MLA
Turabian
Vancouver
Baixar Citação
DOI: http://doi.org/10.14483/23464712.13317
FUNÇÕES QUADRÁTICAS E TECNOLOGIAS MÓVEIS: AÇÕES COOPERATIVAS EM UM EXPERIMENTO NO ENSINO MÉDIO
QUADRATIC FUNCTIONS AND MOBILE TECHNOLOGIES: COOPERATIVE ACTIONS IN AN EXPERIMENT TO TEACHING IN HIGH SCHOOL
FUNCIONES CUADRÁTICAS Y TECNOLOGÍAS MÓVILES: ACCIONES COOPERATIVAS EN UN EXPERIMENTO PARA LA ENSEÑANZA EN EDUCACIÓN MEDIA
Rodrigo Sychocki da Silva*, Shéridan dos Reis Pinto**
Cómo citar este artículo: Sychocki da Silva, R. y dos Reis Pinto, S. (2019). Funções quadráticas e tecnologías móveis: ações cooperativas em um experimento no ensino médio. Góndola, Enseñanza y Aprendizaje de las Ciencias, 14(1), 108-125.
Recibido: 08 de mayo de 2018; aprobado: 27 de junio de 2018
* Doutor em Informática na Educação - UFRGS. Docente permante do Programa de Pós-Graduação em Ensino de Matemática – UFRGS, (Brasil). Correio eletrônico: sychocki.rodrigo@gmail.com - ORCID: https://orcid.org/0000-0002-7406-2517
** Licenciada em Matemática – UFRGS. Discente do Programa de Pós-Graduação em Ensino de Matemática – UFRGS, (Brasil). Correio eletrônico: sherydrp@gmail.com - ORCID: https://orcid.org/0000-0003-2903-803X
Resumo
O presente texto é resultado de uma pesquisa realizada com estudantes do ensino médio e tratou da temática do ensino e aprendizagem de funções quadráticas. O celular, e seu uso em sala de aula, com o aplicativo de matemática instalado foi o propulsor das discussões inerentes às atividades propostas. De cunho qualitativo, a pesquisa procurou analisar como a cooperação entre os estudantes, manifestada a partir de diálogos, construção de conjecturas e argumentação promoveriam a aprendizagem. Após a realização da pesquisa uma consequência, e contribuição, é que o diálogo entre os pares na sala de aula seja um elemento necessário para a aprendizagem da matemática. Notou-se que oportunizar momentos de compartilhamento e enfrentamento de situações de forma conjunta é profícuo para o grupo (coletivo) e também benéfico para o sujeito (individual). Tal metodologia de trabalho diametralmente se afasta da prática unidirecional de transmissão dos conhecimentos em sala de aula, e dessa forma, infere-se sobre a importância de se trabalhar em sala de aula atividades de forma conjunta e com características cooperativas.
Palavras chaves: aprendizagem, escola básica, ensino, matemática.
Abstract
We present the results of a research with high school students and dealt with the topic of teaching and learning quadratic functions. The cell phone, and its use in the classroom, with the math application installed, was the propellant of discussions inherent in the proposed activities. In a qualitative way, the research sought to analyze how cooperation among students, manifested through dialogues, construction of conjectures and argumentation would promote learning. After the research, our consequence contribution is that the dialogue between the peers in the classroom is a necessary element for mathematics learning. It was noted that providing opportunities for sharing and coping with situations together is beneficial for the (collective) group and also important for the individual. Such a work methodology diametrically departs from the unidirectional practice of transmitting knowledge in the classroom, and in this way, it is inferred on the importance of working in classroom activities together and with cooperative characteristics.
Keywords: Learning, Primary School, Teaching, Mathematics.
Resumen
Este trabajo presenta resultados de una investigación realizada con estudiantes de educación media, sobre la temática de la enseñanza y el aprendizaje de funciones cuadráticas. El celular, y su uso en el aula, con la aplicación de matemáticas instalada, fue el propulsor de las discusiones inherentes a las actividades propuestas. De tipo cualitativa, la investigación buscó analizar cómo la cooperación entre los estudiantes, manifestada a partir de diálogos, construcción de conjeturas y argumentación promovería el aprendizaje. Después de la realización de la investigación observamos que el diálogo entre pares en el aula es un elemento necesario para el aprendizaje de las matemáticas. Se notó que propició momentos de compartir y enfrentar situaciones de forma conjunta, lo cual es provechoso para el grupo (colectivo) y también beneficioso para el sujeto (individual). Tal metodología de trabajo se aparta diametralmente de la práctica unidireccional de transmisión de los conocimientos en el aula, y de esa forma, se infiere la importancia de trabajar en el aula actividades de forma conjunta y con características cooperativas.
Palabras clave: aprendizaje, escuela básica, educación, matemáticas.
Introdução
O presente texto, recorte da pesquisa de conclusão de curso de Pinto (2018), propõe uma apresentação, explanação e reflexão sobre o ensino das funções quadráticas fazendo-se uso das tecnologias digitais. O principal objetivo da pesquisa foi analisar como as ações cooperativas entre os estudantes influenciava na aprendizagem das funções quadráticas.
A pesquisa ocorreu fazendo-se uso do software GeoGebra, que é atualmente um software amplamente utilizado por pesquisadores da Educação Matemática em diversas partes do mundo com objetivo de criar e executar estratégias para qualificar o ensino de conteúdos da matemática. Na ocasião para abordar o conteúdo de funções quadráticas por meio do estudo de seus coeficientes pretendeu-se analisar como era construído o conhecimento da matemática dando-se ênfase à cooperação entre os pares na sala de aula. Com isso, a pergunta central da pesquisa foi: Como a cooperação entre os sujeitos influencia na aprendizagem das funções quadráticas por meio do estudo de seus coeficientes?
Norteados a partir da leitura de pesquisas e documentos diretrizes para a educação no Brasil e também pela realização de práticas de ensino no âmbito de outras disciplinas da graduação em Licenciatura em Matemática notou-se que o conteúdo de funções reais de variável real é visto inicialmente pelos alunos da Educação Básica e eventualmente se estende até os cursos universitários. Portanto, considerou-se viável criar e refletir sobre uma prática de ensino na Educação Básica, a qual pudesse contribuir na formação inicial dos estudantes da escola sobre o assunto.
A escolha do tema desta pesquisa, justificada pela união da matemática com as tecnologias digitais, utiliza-se da ideia de que o ensino das funções quadráticas possa ocorrer por meio do uso de tecnologias digitais móveis, já que foi constatado emergente e atualmente crescente o número de dispositivos móveis que os estudantes tem acesso. Buscou-se analisar como a construção dos conhecimentos pode ocorrer a partir da cooperação entre os estudantes. A partir de um desenho metodológico qualitativo houve a elaboração e execução de uma sequência de atividades que explorava o tema função quadrática. As atividades foram realizadas no Colégio de Aplicação da Universidade Federal do Rio Grande do Sul, com estudantes do 1º ano do Ensino Médio, no ano de 2017.
A partir do nosso entendimento, no qual o estudante deva ser o protagonista no espaço da sala de aula, entende-se que essa pesquisa possa contribuir no planejamento pedagógico do professor, considerando o desenvolvimento e valorização de ações autônomas e de senso crítico dos estudantes. Portanto, considera-se que a discussão e polinização das ideias aqui tratadas torna-se relevante, pois busca se inserir e contribuir para uma Educação Matemática com suporte nas tecnologias digitais móveis, com ênfase na formação de cidadãos críticos e autônomos.
1. Fundamentos teóricos & revisão de literatura
Os Parâmetros Curriculares Nacionais do Ensino Médio – PCNEM (Brasil, 2002), manifestam que o conhecimento inerente as funções oportuniza ao estudante a construção de uma linguagem algébrica que é fundamental para expressar relações entre grandezas e investigar situações-problema, por meio da construção de modelos descritivos dos fenômenos e consentindo conexões na matemática e fora dela. Além disso, os PCNEM (Brasil, 1999) destacam a importância da representação gráfica das funções quadráticas, referente à interpretação de sua forma algébrica, enfatizando que:
O estudo dessa função – posição do gráfico, coordenadas do ponto de máximo/mínimo, zeros da função – deve ser realizado de forma que o aluno consiga estabelecer as relações entre o “aspecto” do gráfico e os coeficientes de sua expressão algébrica, evitando-se a memorização de regras. (Brasil, 1999 p. 72)
É valorizada a utilização da tecnologia nas aulas de matemática, visto que a mesma “deve acompanhar criticamente o desenvolvimento tecnológico contemporâneo, tomando contato com os avanços das novas tecnologias nas diferentes áreas do conhecimento para se posicionar frente às questões de nossa atualidade” (Brasil, 2002 p. 118). Ainda é mencionado que ao inserir e fazer uso das tecnologias permite-se afirmar que aprender matemática no Ensino Médio deve ser mais do que memorizar resultados dessa matéria e que o conhecer matemático deve estar ligado ao saber fazer matemática e de um “saber pensar matemático” (Brasil, 1999 p. 41).
Inserido em um contexto de sala de aula, a partir de um olhar sobre o trabalho cooperativo entre os estudantes, as diretrizes mencionam que um dos objetivos da aprendizagem matemática no nível médio seja “promover a realização pessoal mediante o sentimento de segurança em relação às suas capacidades matemáticas, o desenvolvimento de atitudes de autonomia e cooperação” (Brasil, 1999, p. 42). O trabalhar cooperando também é destacado pelas diretrizes com a ênfase que esse tipo de exercício faz com que a aprendizagem das Ciências e da Matemática torne-se mais eficaz.
Ainda é mencionado pelas diretrizes que a aprendizagem não se dá com o estudante afastado, sem viabilidade de relacionar-se com os colegas e professor, mas em conjunto, demonstrando para si e para os outros seus pensamentos e argumentos. Assim, ao trabalharem coletivamente é exercida a comunicação oral. Em suma:
A Matemática deve ser compreendida como uma parcela do conhecimento humano essencial para a formação de todos os jovens, que contribui para a construção de uma visão de mundo, para ler e interpretar a realidade e para desenvolver capacidades que deles serão exigidas ao longo da vida social e profissional. (Brasil, 2002 p. 111)
Assim, reunindo-se as informações sobre o que as diretrizes enunciam, o estudo da matemática deve contribuir para a formação global do estudante, e que o mesmo seja capaz de fazer leituras de mundo com uma melhor apreensão a partir do saber pensar matemática. Entende-se, consoante com o proposto nas diretrizes que o trabalho coletivo entre os estudantes com a utilização da tecnologia, cria condições para o aprendizado desse conteúdo matemático.
Consoante ao que as diretrizes curriculares brasileiras consideram foi feita durante a pesquisa uma revisão de literatura. A consulta, reflexão e exposição de pesquisas realizadas que versam o tema abordado, ensino de funções quadráticas por meio de mídias digitais, buscam apresentar um recorte sobre como a comunidade de pesquisadores em Educação Matemática posiciona-se e reflete diante do desafio de ensinar com o suporte das tecnologias digitais.
A utilização do software GeoGebra segundo Borba, Gadanidis, Silva (2014) sugere que tal aplicação se aproxima ao uso de lápis e papel sobre o que é aprendido em matemática além de propiciar a “experimentação, visualização e de heurística dos humanos envolvidos nesse coletivo” (Borba, Gadanidis, Silva, 2014 p. 73). Devido a isso ao fazer uso do software GeoGebra no ensino de funções, Bortolossi, Pesco e Resende (2012, apud Borba, Gadanidis, Silva, 2014 p. 48), afirmam:
No GeoGebra, pontos podem ser criados sobre gráficos de funções de modo que, ao movê-los, eles continuem sempre sobre o gráfico da função. Os valores das coordenadas desses pontos podem ser então recuperados e usados em cálculos ou na criação de outros elementos geométricos (pontos, segmentos e retas). Esse tipo de recurso permite ao usuário estudar (graficamente, algebricamente e numericamente) como, por exemplo, características locais da função (taxas de variação média e instantânea) mudam de acordo com a posição do ponto sobre o gráfico da função. (Bortolossi, Pesco, Resende, 2012 p. 78)
Com vistas a possibilitar a construção do conhecimento por meio do aproveitamento dos instrumentos digitais atuais, Borba, Gadanidis, Silva (2014) refletem que a experimentação deva fazer parte do processo de apreensão e aprendizagem das ideias matemáticas. Os autores destacam que é necessário planejar e implementar um “design experimental” (Borba, Gadanidis, Silva, 2014 p. 50) ao se realizar atividades de matemática. Nas palavras, dos autores “dessa forma, buscamos formar cenários de investigação matemática, ou seja, um ambiente heurístico, de descobertas, de formulação de conjecturas acerca de um problema e busca por possíveis e diversificadas soluções.” (Borba, Gadanidis, Silva, 2014 p. 50).
Giraldo, Guimarães, Muruci (2008) por meio da utilização do software Tabulae, analisaram o desenvolvimento das representações algébricas, gráficas e numéricas de funções. As atividades do minicurso envolviam a exploração dos esboços gráficos das funções reais no software. Os autores apresentam uma opção de proposta didática para os professores realizarem em suas salas de aula. Sobre as atividades elaboradas:
Ao longo dessas atividades os participantes serão levados à compreensão do processo de construção do gráfico de funções, sendo capazes de construir os seus próprios gráficos, utilizando as funcionalidades do ambiente. Esta construção envolve vários conceitos matemáticos, como translações e rotações, vetores, produto de escalar por vetor, lugar geométrico, parâmetros e variáveis, o que efetivamente contribuirá para um entendimento mais abrangente e aprofundado de diversos aspectos e propriedades relacionadas a sistema de coordenadas, funções e seus gráficos. (Giraldo, Guimarães, Murici, 2008 p. 3)
Caires, Nascimento (2012) realizaram uma pesquisa qualitativa com atividades sobre funções e utilizaram o computador, por meiodo software Kmplot. Os autores refletem sobre o uso da mídia digital em sala de aula:
O uso de diferentes esquemas se mostrou útil na assimilação de parte do conteúdo. Procurou-se através do suporte computacional, um esquema de trabalho que ajudasse aos alunos romperem a barreira da representação, que eles encontraram no momento de fazer a representação gráfica de polinômios de primeiro grau e também dos polinômios de segundo grau. Mesmo visualizando no quadro os resultados mostrados através de exemplos, há uma dificuldade apresentada pelos discentes na representação das funções afim e quadrática a partir da plotagem. (Caires, Nascimento, 2012 p.407)
Santos, Silva, Soares (2012) em seu estudo buscaram por meio do uso do software WinPlot ensinar conteúdos matemáticos. Os autores elaboraram uma sequência de atividades com o software a qual propunha a análise dos parâmetros das funções afim e quadrática. Sobre a contribuição que a pesquisa tem, os autores mencionam:
Os resultados dessa pesquisa comprovam que o computador é uma importante ferramenta de motivação, e mostra quanto é importante inovar nas aulas para torná-las mais atrativas e dinâmicas. O dinamismo oferecido pelo software contribuiu significativamente para o desenvolvimento da aprendizagem dos alunos participantes. (Santos, Silva, Soares, 2012 p. 204)
Consoante a citação anterior, Bona, Lutz (2015) em um estudo realizado num curso de especialização em Educação Matemática pesquisaram sobre o ensino do conteúdo gráficos da função quadrática por meio da utilização de tecnologias e a recepção dos discentes quanto à proposta. A atividade foi construída com a ênfase de comparações entre diversos gráficos da função quadrática e o estudo dos coeficientes da função, com o auxílio do software Winplot. Colet (2015) utilizou a Engenharia Didática para uma pesquisa com foco no desempenho dos coeficientes da função quadrática por meio da aplicação do software Winplot destacando que “(...) é importante que o professor se alie a diferentes recursos e metodologias de ensino para poder abranger a diversidade de alunos existentes em uma mesma turma, considerando suas dificuldades e limitações.” (Colet, 2015 p. 10). Sobre o uso das tecnologias, em suas conclusões a autora menciona que a “utilização dessas ferramentas tem se mostrado essencial para ampliar o conhecimento de conteúdos em estudo e desenvolver nos alunos novos hábitos de pensamento, autonomia e poder de investigação na realização das atividades.” (Colet, 2015 p. 20).
Em um estudo que investigou e analisou atividades de dois livros didáticos sobre a introdução de funções quadráticas especificando seu diagnóstico nas representações gráficas e algébricas dessas funções Lopes (2013) verificou que há uma descrição sobre as duas representações, e constatou que houve a ausência da conversão entre elas. Então, a partir de cada atividade do livro didático analisado, a proposta de pesquisa consistiu em alternativas de atividades realizadas com o software que utilizam o estudo dos parâmetros das funções quadráticas. Nesse sentido, Araújo, Silva (2016) relatam sobre a preocupação dos docentes em tornar visível aos estudantes conteúdos de maior abstração da matemática. Nesse sentido, foi elaborada uma proposta de atividade com a utilização do software GeoGebra para o ensino de funções quadráticas. Sobre o uso das tecnologias e a relação disso com o fazer docente os autores contribuem:
A tecnologia em sala de aula é grande aliada dos professores no que diz respeito ao processo de ensino aprendizagem, o uso dos softwares matemáticos, faz o docente refletir sobre sua própria prática, ou seja, levar o docente repensar suas atitudes. É preciso que o professor tenha vontade e desejo de mudança. (Araújo, Silva, 2016 p. 5)
Quanto à criação de materiais para o ensino de matemática Bortolossi, Pesco, Rezende (2012) em seu artigo focaram na utilização do software GeoGebra para oportunizar uma metodologia de trabalho dinâmico do ensino de funções afins, quadráticas e exponenciais. As atividades sobre os três tipos de funções envolviam o estudo das variações de seus coeficientes. Ainda nessa temática, Silva (2014) em seu estudo buscou introduzir a utilização do software GeoGebra no ensino de funções quadráticas. Foram realizadas atividades com foco no estudo dos gráficos e coeficientes.
Medeiros, Schardosim (2011) trataram sobre uma proposta didática para a exploração do conceito de funções quadráticas com o auxílio do software GeoGebra. O objetivo da proposta foi estimular a curiosidade, a imaginação e a construção de diferentes caminhos para a resolução de problemas e o desenvolvimento das capacidades de abstração. Foram realizadas atividades com problemas de área e a construção das leis que expressavam as funções. Em seguida os estudantes interagiram com o software e os coeficientes das funções quadráticas. A utilização do software no ensino da função quadrática oportunizou a construção dos conceitos matemáticos apresentados nas atividades, na qual “o aluno trabalha com o processo algébrico e também geométrico das funções do tipo y= ax²+bx+c (...)” (Medeiros, Schardosim, 2011 p. 10).
Amaral, Filho, Nogueira (2014) descrevem uma atividade utilizando o software GeoGebra no ensino de funções quadráticas com ênfase na representação gráfica. Em cada atividade realizada, os estudantes analisaram os esboços gráficos obtidos com ênfase nas raízes das funções. Sobre o papel do professor no processo os autores refletem que o mesmo “tem papel fundamental no processo de ensino-aprendizagem já que apenas com informática o aluno não conseguiria construir o conhecimento de maneira sólida. O professor deve então ser o mediador de todo processo de construção do conhecimento” (Amaral, Filho, Nogueira 2014 p. 11). Por fim, Ricardo (2012), em sua dissertação traz uma proposta para o ensino de funções quadráticas, utilizando o software GeoGebra. O autor teve como objetivo desenvolver, analisar e avaliar uma proposta de ensino mediada pela tecnologia no estudo de funções quadráticas. A análise dos dados e reflexões foi feita durante as atividades. Em relação ao papel de cada coeficiente, os estudantes, com suas palavras respondiam o que acontecia com o gráfico da função à medida que alteravam os coeficientes. O autor reflete que a proposta “se enquadra no que planejamos não um trabalho que tenha finalidade de ensinar o conteúdo, mas um trabalho que sirva como apoio.” (Ricardo, 2012 p. 110). O mesmo ainda concluiu com a pesquisa que os discentes estão aptos e dispostos a conhecer algo novo, no qual seja usado pelo professor em sala de aula um método de trabalho diferenciado.
A fundamentação teórica e revisão de literatura enriqueceram a construção da presente proposta, visto que o estado da arte direcionava para o alcance das metas e objetivos inicialmente propostos. O fato é que a abordagem de funções quadráticas a partir de uma metodologia de trabalho que oportunizasse momentos de ação e reflexão por parte dos estudantes, estruturava-se como um desafio a ser encarado. A partir do cenário teórico estabelecido mostrou-se emergente conhecer e se apropriar das ideas de Piaget sobre ação cooperativa. A próxima seção explanará sobre a temática.
2. Sobre “cooperação”: um olhar nas ideias de Piaget
As articulações entre os fazeres individuais e coletivos dos estudantes envolvidos na pesquisa constituíramum elemento de incomensurável importância para o exercício da reflexão sobre o fazer docente em sala de aula. Para tal, foi necessário conhecer e explanar as ideias de Jean Piaget sobre cooperação. Nas palavras do autor:
A cooperação consiste ela mesma num sistema de operações, de tal forma que as atividades do sujeito se exercendo sobre os objetos, e as atividades dos sujeitos quando agem uns sobre os outros se reduzem na realidade a um só e mesmo sistema de conjunto, no qual o aspecto social e o aspecto lógico são inseparáveis na forma como no conteúdo. (Piaget, 1973 p. 103)
A cooperação “é operar em comum, isto é, ajustar por meio de novas operações (...) de correspondência, reciprocidade ou complementaridade.” (Piaget, 1973 p. 105). Ou seja, cooperação em uma discussão de um grupo de estudantes sobre um determinado assunto matemático, por exemplo, pode ser exercida pela troca de ideias e pensamentos desses estudantes sobre o mesmo. Além disso, Bona (2012) salienta:
A cooperação é um processo de aprendizagem criador de realidades novas, de novas perspectivas sobre um assunto de matemática, por exemplo, e não apenas um meio de trocas entre estudantes. Esse processo é viabilizado pelas tecnologias digitais em atividades sincrônicas e assincrônicas. (Bona, 2012 p. 63)
A criação de novas realidades oportuniza aos estudantes a reflexão e “o desenvolvimento das operações racionais supõe uma cooperação entre os indivíduos liberando-os de seu egocentrismo intelectual inicial.” (Piaget, 1973 p. 83). Camargo, Becker (2012 p. 529) discorrem sobre a cooperação segundo Piaget. Esse percurso, tal como apresentado pelos autores, é dividido em quatro períodos. Primeiramente há o pensamento infantil: “a cooperação é explicada como um tipo de relação que permeia a autonomia moral”. Em um segundo momento o pensamento precede a linguagem: a cooperação é encontrada “na explicação do desenvolvimento do egocentrismo para a descentração cognitiva”. No terceiro período mostra-se presente o conceito de operação: “cooperação é relacionada com coordenação de pontos de vista”. E por fim, no quarto período a “cooperação está relacionada à explicação da abstração reflexionante”.
Piaget em suas notas discorre sobre o trabalho em equipes nas escolas e critica a visão de senso comum de que a escola seja considerada um local de “transmissão do conhecimento”. O autor considera que “sendo o mestre detentor dos conhecimentos exatos às técnicas a adquirir, o ideal é a submissão da criança a sua autoridade e todo contato intelectual das crianças entre si não comporta senão perda de tempo e riscos de deformações e erros” (Piaget, 1993 p.3). Portanto, mostra-se assim uma dificuldade de o professor fazer o aluno compreendê-lo, pois “a criança não é um ser passivo, do qual se trate de rechear o cérebro, mas um ser ativo, cuja tendência à pesquisa espontânea tem necessidade de alimentos” (Piaget, 1993 p. 3). Com isso, nota- -se que para a evolução das relações nos espaços escolares seja necessário, porém não suficiente, cooperar. Nas palavras do autor:
A cooperação não age somente sobre a tomada de consciência do indivíduo e sobre o seu senso de objetividade, mas termina, afinal, por constituir toda uma estrutura normativa que remata sem dúvida o funcionamento da inteligência individual, mas completando- a no sentido da reciprocidade. (...) A cooperação é verdadeiramente criadora, ou o que vem a ser o mesmo, constitui a condição indispensável para a completa formação da razão. (Piaget, 1993 p. 8)
Assim, pôde-se compreender, a partir da leitura e apreensão das ideias de Piaget, que a cooperação em ações coletivas oportunizaram reflexões e posterior construção de conhecimentos matemáticos pelos estudantes. Dessa forma, tal aporte mostrou- -se como necessário no entendimento sobre como os participantes da pesquisa, estudantes do ensino médio regular, estavam agindo e reagindo de forma cooperativa, e com isso promovendo a construção do conhecimento sobre funções quadráticas para si.
3. Fundamentos Metodológicos: materiais e métodos
As atividades foram elaboradas com foco no estudo das funções quadráticas por meio da variação dos parâmetros utilizando o software GeoGebra Graphing Calculator. Além da exploração com a tecnologia, cada questão foi construída com o intuito de provocar, a partir do trabalho coletivo, as reflexões dos participantes buscando a construção de uma resposta para a pergunta central da pesquisa e apresentada na introdução desse texto. A caracterização metodológica da pesquisa foi qualitativa, a qual converge para o pensamento de Flick (2009):
Os aspectos essenciais da pesquisa qualitativa consistem na escolha adequada de métodos e teorias convenientes; no reconhecimento e na análise de diferentes perspectivas; nas reflexões dos pesquisadores a respeito de suas pesquisas como parte do processo de produção de conhecimento; e na variedade de abordagens e métodos. (Flick, 2009 p. 23)
Além disso, Bodgan, Biklen (1994) citam as cinco características de uma pesquisa qualitativa, as quais foram utilizadas no presente estudo. As características serão explanadas a seguir.
Característica 1: A fonte dos dados é o ambiente natural, tomando o investigador como o objeto principal:
Os investigadores qualitativos frequentam os locais de estudo porque se preocupam com o contexto. Entendem que ações podem ser melhor compreendidas quando são observadas no seu ambiente habitual de ocorrência. (...)Os investigadores qualitativos assumem que o comportamento humano é significativamente influenciado pelo contexto em que ocorre, deslocando-se, sempre que possível, ao local de estudo. (Bodgan, Biklen, 1994 p.48)
Característica 2: A pesquisa qualitativa é descritiva, ou seja, “os dados recolhidos são em forma de palavras ou imagens e não de números. Tentam analisar os dados em toda a sua riqueza, respeitado, tanto quanto o possível, a forma em que os dados foram registrados ou transcritos.” ( Bodgan, Biklen, 1994 p.48).
Característica 3: Em pesquisa qualitativa há predominantemente “interesse no processo da pesquisa do que pelos resultados” (Bodgan, Biklen, 1994 p.49).
Característica 4: Há uma tendência de análise dos dados de forma indutiva:
Não recolhem dados ou provas com o objetivo de confirmar o infirmar hipóteses construídas previamente; ao invés disso, as abstrações são construídas à medida que os dados particulares que foram recolhidos se vão agrupando. (...) Está-se a construir um quadro que vai ganhando forma à medida que se recolhem e examinam as partes. (Bodgan, Biklen, 1994 p.50)
Característica 5: Destaca-se a importância do significado: “os investigadores que fazem uso deste tipo de abordagem estão interessados no modo como diferentes pessoas dão sentido às suas vidas” (Bodgan, Biklen, 1994 p.50).
A pesquisa se caracterizou por ser qualitativa, pois analisou como a cooperação influenciava na aprendizagem das funções quadráticas, a partir das observações nos tipos de discussões matemáticas que emergiamdos estudantes quando eram organizados para trabalharem em grupos.
A sequência de atividades foi aplicada durante o período da disciplina de Estágio em Educação Matemática III (EDU02X15) no curso de Licenciatura em Matemática da Universidade Federal do Rio Grande do Sul. No contexto, os estudantes, participantes da pesquisa, já haviam iniciado o estudo sobre a função afim, sendo que a próxima seria a função quadrática. A escola, lócus da pesquisa, foi o Colégio de Aplicação da Universidade Federal do Rio Grande do Sul. A turma participante do experimento era uma turma de Ensino Médio regular do primeiro ano. A faixa etária do grupo estava entre os 15 e 17 anos. A coleta dos dados foi feita a partir do registro escrito pelos estudantes durante as atividades e também por meio de gravação de aúdio.
A escola dispunha na época de laboratório de informática com 20 máquinas todas com acesso à internet. Porém, devido aconstante lotação da sala de informática da escola durante a prática, foi necessário pensar numa alternativa para tornar exequível a sequência de atividades. Como na ocasião a escola tinha rede Wireless de internet, os estudantes poderiam utilizar o celular para fazer o download do aplicativo GeoGebra Graphing Calculator1, que dispõe de interface para esboçar gráficos. O aplicativo pode ser obtido por meio das plataformas de aplicativos de smartphones. Na figura 1 mostra-se o layout do aplicativo depois de instalado no celular:
Na tabela 1 a seguir estão dispostas quais foram as atividades e o cronograma de execução em que ocorreram. As atividades foram pensadas de acordo com os objetivos inicialmente pensados. Cada uma das atividades e exercícios versava estimular discussões, as quais entende-se que estimulariam reflexões por parte dos estudantes.
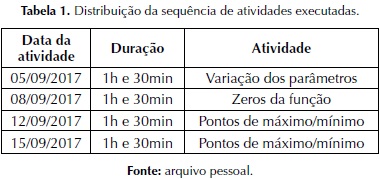
A primeira atividade (Variação de parâmetros) iniciou-se com um pequeno manual sobre a utilização do aplicativo GeoGebra Graphing Calculator. As instruções foram úteis para os durante a realização das tarefas. As atividades seguiram-se após os estudantes inserirem no campo de entrada a função: f(x) = ax²+bx+c. A primeira questão objetivou que os participantes conseguissem entender o papel de cada parâmetro no gráfico da função, por meio das variações de a, b e c utilizando a ferramenta controle deslizante do aplicativo.
A segunda questão exigiu que os estudantes já tivessem compreendido quais os parâmetros que acompanhavam as variáveis da lei da função. A última questão forneceu o gráfico e solicitou que os sujeitos encontrassem os parâmetros que constituíam a lei de cada uma. A resolução dessa questão exigiu que os estudantes soubessem resolver sistemas de equações, pois para obter os parâmetros a e b com o conhecimento recentemente explorado, necessitou tal método de resolução.
Todas as questões elaboradas da primeira atividade incitavam cooperações, as quais estimulavam o exercício da autonomia dos estudantes, o trabalho em conjunto e a atribuição da tecnologia para promover a construção do conhecimento sobre o papel de cada parâmetro no gráfico da função quadrática. Desejou-se que os participantes, por meio do trabalho coletivo conseguissem conjecturar e verificassem as hipóteses durante o desenvolvimento da atividade.
A partir da definição dos zeros da função quadrática (Zeros da função) os estudantes analisaram os gráficos, localizaram e identificaram as raízes em cada um. Em cada função apresentada na primeira questão era possível encontrar os zeros a partir da análise gráfica, sem ser necessário efetuar cálculos. Na segunda questão, objetivou-se que eles analisassem cada gráfico e refletissem se fosse possível encontrar os zeros da função sem efetuar cálculos e na terceira questão, a proposta foi de que os participantes explorassem a relação entre essas duas questões. As relações evidenciaram-se na construção dos argumentos para a quarta questão. Após as discussões e o conhecimento explorado durante as questões anteriores, na quinta questão a proposta era aplicar os conhecimentos até o momento construídos para indicar a lei da função que fosse gerar cada gráfico.
A atividade (Pontos de máximo/mínimo) foi composta de seis questões sobre os conceitos de pontos mínimo e máximo de uma função quadrática. Essa atividade explorou a simetria da parábola. Na segunda questão dessa atividade, os estudantes já tendo explorado a simetria da parábola, deveriam intuir as coordenadas dos pontos de máximo ou mínimo de cada gráfico esboçado no GeoGebra móvel. Objetivou-se com essa questão que os participantes conseguissem construir conjecturas de como calcular as coordenadas dos pontos máximo/ mínimo dos gráficos.
Aspirou-se que os estudantes conseguissem encontrar os pontos de máximo/mínimo, na terceira questão, e além a provocação foi para que os sujeitos refletissem sobre a questão: toda parábola tem ponto de máximo/mínimo? Nas questões quatro e cinco, objetivou-se que os estudantes percebessem de que há infinitas parábolas com mesmo ponto de máximo/mínimo. Por meio da análise de que os parâmetros da função variam, e de que podem variar mantendo os mesmos pontos de máximo/mínimo. A sexta questão explorou o conhecimento dos estudantes da parábola e o papel dos parâmetros no gráfico. Assim, eles deveriam concluir que somente o parâmetro a possibilita a existência da parábola.
A partir disso, por meio do trabalho em conjunto, observando-se cooperações, com a utilização do software GeoGebra Graphing Calculator buscou-se além das investigações das atividades propostas, oportunizar o exercício e desenvolvimento da autonomia dos participantes. É importante mencionar, aos interessados na proposta, que todas as atividades e questões supracitadas podem ser consultadas e acessadas de forma integral em Pinto (2018). Tal disponibilidade de acesso visa alcançar profesores e demais interessados em conhecer e aplicar tal sequência de atividades.
4. Análises pós experimentos
A análise das atividades foi feita na ordem em que foram aplicadas. Apresentam-se os resultados do experimento por meio das transcrições de trechos de áudios de dois grupos da turma. Esses áudios exemplificam como os estudantes conjecturaram e refletiram sobre as questões propostas. Como o presente artigo trata-se de um recorte de uma pesquisa mais ampla (Pinto, 2018), escolheu-se apresentar uma diagonal da análise produzida a partir do primeiro dia de experimento, ou seja da atividade “Variação dos parâmetros”.
No primeiro momento, a professora pesquisadora entregou a primeira atividade e deixou que os estudantes lessem e se familiarizassem com a mesma. Todos pareceram saber utilizar o GeoGebra Gaphing Calcultor e não manifestaram dúvidas. Pode-se afirmar que durante toda a execução da sequência de atividades houveram discussões e a manifestação de argumentos por parte dos estudantes, ou seja, um importante acolhimento e dedicação dos participantes diante da proposta.
Diante do referencial estudado, inferiu-se que a cooperação fosse um fator que estimulasse as discussões dos estudantes que em conjunto trabalharam na investigação e resolução de situações-problema. Tal fato ocorreu nas passagens apresentadas no quadro 1, em que os estudantes discutiram e analisaram o esboço do gráfico de uma função. Quando a função não tem raízes reais, seu gráfico não intercepta o eixo x. O estudante A trouxe esse apontamento na discussão da resposta do item (b). Sobre a intervenção da professora, ela auxilia da forma que eles tentem conjecturar e discutir sobre o papel do parâmetro b. Então, os estudantes foram orientados a observar a linha de corte do eixo y. Nesse momento o aluno B, conseguiu inferir sobre o papel do parâmetro no gráfico.

Borba, Gadanidis, Silva (2014), e Borba, Penteado (2002), enfatizam a importância da utilização das tecnologias digitais nas aulas de matemática. Percebeu-se que devido a exploração do GeoGebra Graphing Calculator pelos estudantes, conjecturas matemáticas foram criadas. A mediação da professora durante a aula, na condução das atividades, oportunizou aos estudantes desenvolver confiança própria, ou seja, à medida em que avançavam nas discussões dos problemas mais intensas eram as trocas e ações em conjunto entre os pares na sala de aula. Constatou-se que o uso da tecnologia digital tenha sido profícuo para os estudantes nesse sentido, sendo que a mesma oportunizou e estimulou a participação na construção e verificação de conjecturas no momento das atividades.
No quadro 2, ao variarem o parâmetro c, a primeira conjectura foi elaborada pelos estudantes. “Positivo ou negativo” demonstra o que os mesmos veem, o deslocamento vertical para baixo e para cima é o que eles enxergam. Após eles pensarem em negativo e positivo, o estudante B cita o para baixo e para cima. Percebe-se na discussão entre o grupo, que mesmo com o uso de palavras coloquiais, eles manifestam verbalmente o que estão apreendendo sobre o parâmetro. Estendendo a ideia para o trabalho desenvolvido em sala de aula pelo professor, em consoância com as ideias de Piaget (1973), isso torna possível a cada sujeito libertar-se de seu egocentrismo intelectual, compartilhando e construindo coletivamente conhecimentos.

Novamente Piaget (1973), citado na fundamentação teórica do artigo, enuncia cooperação como o “operar em comum” (p. 105) reajustando ações por “correspondência, reciprocidade ou complementaridade” (p. 105). Percebe-se esses reajustes no quadro 2 anterior, os argumentos, negativo ou positivo, contrariam a opinião do estudante A. Na passagem o estudante A manifesta insatisfação enfatizando que apenas o parâmetro a indica se o gráfico é “positivo ou negativo”, enquanto os estudantes B e C argumentam que o gráfico se desloca verticalmente. Trata-se de um alinhamento e processo gradual de construção de conhecimentos, por meio de ajustes e argumentação individual perante o coletivo.
No quadro 3 acima, o ajuste de ações ocorreu e os estudantes entraram em acordo; concluíram que o parâmetro c indicava a coordenada y quando x = 0. Destaca-se que a questão 1 foi resolvida pela análise gráfica com o GeoGebra Graphing Calculator. Durante a exploração do grupo no aplicativo, os estudantes trabalharam em conjunto em prol da compreensão da questão e puderam conjecturar, explorar, analisar, inferir e (re)construir hipóteses sobre os parâmetros da função quadrática. Menciona-se que durante toda a execução das atividades houve diversas ações articuladas individuais e em conjunto, já exemplificadas nos quadros anteriores, e isso confirmou uma das hipóteses da pesquisa mencionadas anteriormente, a qual cita que em termos de evidenciar a aprendizagem, tais condutas em sala de aula tornam-se elementos profícuos para isso ocorra. Além disso, entende-se que durante todo o trabalho conduzido pela professora e autora desse artigo, com a cooperação potencializada, o trabalho docente afastou-se de uma prática unidirecional transmissora de conhecimentos.

A questão apresentada na figura 2 anteriormente explorou o entendimento de onde se localizavam os parâmetros a, b e c na lei de formação da função explicitada. Os dois grupos não registraram suas falas nessa questão. Entende-se que os grupos tenham transcrito para o material impresso as observações feitas na tela do celular. Sobre a questão três dessa atividade, o debate está transcrito no quadro 4, a seguir.


Como foi observado no trecho acima, no início da questão, o grupo necessitou de uma intervenção da professora para explicar como eles encontrariam os parâmetros a e b. Porém, eles conseguiram, por meio da análise gráfica conjecturar e verificar que o parámetro c tinha um valor e qual seria o sinal do parâmetro a. Com o objetivo de construir uma solução, os estudantes articularam outros conhecimentos matemáticos, por exemplo, a resolução de sistemas lineares. Tais conhecimentos foram necessários para o encaminhamento e reflexão das respostas construídas. Durante todo momento os grupos manifestaram e articularam ações em forma coletiva para avançar na construção e interpretação da questão proposta. Verifica-se que os ajustes e argumentação matemática, frutos de ações individuais dentro de um contexto coletivo, influenciaram os debates, construção e mobilização de saberes matemáticos. Os estudantes, a partir de discussões, avançaram na direção do conhecimento e isso é uma qualidade do trabalho desenvolvido em conjunto. Quando é possibilitado ao sujeito contribuir com ideias e argumentar sobre o que está pensando, além de promover e evidenciar a própria aprendizagem, influencia e contribuiu para que os demais também sejam mobilizados a pensar sobre o assunto em debate. Evocando novamente Piaget (1993) o qual afirma:
A cooperação não age somente sobre a tomada de consciência do indivíduo e sobre o seu senso de objetividade, mas termina, afinal, por constituir toda uma estrutura normativa que remata sem dúvida o funcionamento da inteligência individual, mas completando-a no sentido da reciprocidade. (...) A cooperação é verdadeiramente criadora, ou o que vem a ser o mesmo, constitui a condição indispensável para a completa formação da razão. (Piaget, 1993 p.8)
Pode-se inferir que a cooperação entre os pares observada ao longo da realização das atividades foi o combustível para a discussão e construção de ideias matemáticas. Abaixo, na figura 3, ilustra-se a resolução proposta de forma articulada e coletiva pelo grupo:
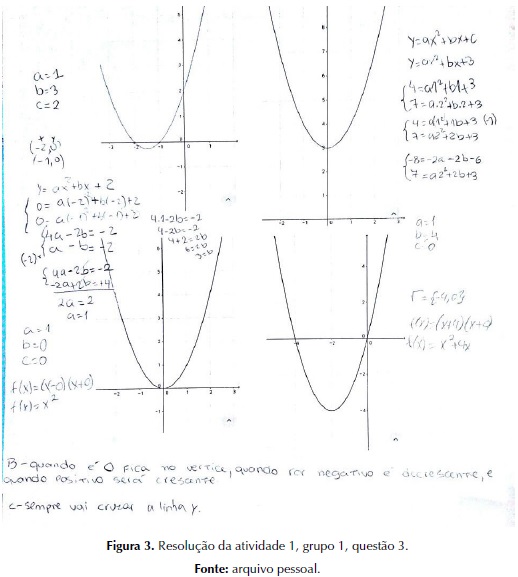
Os áudios analisados na atividade 1 mostram a integralização do grupo elencando discussões e conjecturas com o intuito de debater sobre as questões. O trabalho coletivo oportunizou que eles ajustassem suas ações e construíssem coletivamente os argumentos matemáticos.
O trechos mostrados nos quadros anteriores exemplificam a ocorrência do conceito de cooperação apresentado Piaget (1973), no qual, a partir das ações dos sujeitos uns sobre os outros, a construção de uma resposta final emerge a partir de discussões e refinamentos no processo argumentativo em matemática. Após a análise das resoluções por áudios e em papel dos grupos participantes do experimento constatou-se que houve cooperações nos mais diversos níveis e intensidades. Ao cooperarem em prol de construir respostas para as atividades propostas, os grupos conseguiram mobilizar e construir saberes sobre os aspectos gráficos e algébricos das funções quadráticas.
Por meio da utilização do GeoGebra Graphig Calculator os estudantes conseguiram visualizar o que estava acontecendo no momento da variação dos parâmetros. A partir disso responderam com suas palavras a função de cada coeficiente no gráfico da função. Percebeu-se que o grupo de estudantes conseguiu aplicar os conhecimentos construídos do início ao fim das atividades propostas.
Além disso, o uso da tecnologia digital desempenhou um papel importante e evidenciou a aprendizagem, uma vez que foi por meio da análise gráfica que os mesmos conseguiram responder a maior parte das questões. Borba, Gadanidis, Silva (2014) defendem a utilização e a exploração dessa tecnologia dentro da sala de aula, assim como as diretrizes curriculares nacionais, admitindo-se que o ensino da Matemática deva acompanhar o avanço tecnológico, com a iserção e uso de diferentes tecnologias nas aulas dessa ciência.
Durante a realziação da pesquisa observou-se que a inserção da tecnologia nas aulas de matemática vem sendo explorada nos livros didáticos do Brasil, apesar de não ter sido o foco de análise do presente texto. Mesmo que os exemplares apenas a utilizem para visualização, percebe-se que a tecnologia pode se fazer presente nas salas de aula. Portanto, o objetivo, elencado pelas diretrizes curriculares nacionais brasileiras (Brasil, 2002), de que os estudantes possam aprender sem memorização de regras e fórmulas, ainda é aspirado e não foi plenamente alcançado nos dias de hoje.
Por fim, a partir dos dialógos e ações coletivas dos estudantes no decorrer das atividades, percebeu- se nas transcrições dos áudios de cada grupo, que a construção de hipóteses, verificação e argumentação matemática oportunizou a construção de conceitos matemáticos. As discussões, mediadas pela professora e investigadora, procuraram estimular o fazer discente, tornando o estudante protagonista do aprendizado. A análise e reflexão a partir do referencial teórico apresentado oportunizaram refletir também sobre a prática docente, a qual deve valorizar a interação e fazer coletivo dos estudantes, em oposição à transmissão unidirecional do conhecimento em sala de aula.
5. Reflexões finais
A revisão de literatura e consulta as diretrizes curriculares brasileiras oportunizou perceber e refletir sobre uma falta de harmonia entre o que enfatizam as diretrizes e a construção do conhecimento pelos estudantes, o qual se almeja minimizar a memorização de regras e fórmulas. Posteriormente, na tentativa de responder a pergunta central desse trabalho, elaborou-se uma sequência de atividades que fosse sobre funções quadráticas utilizando tecnologia móvel (GeoGebra Graphing Calculator) e os sujeitos da pesquisa fossem estudantes da escola básica. A partir da análise do referencial teórico estudado, optou-se por organizar os participantes em grupos, com o objetivo de observar o processo cognitivo no decorrer da experimentação de ensino.
Tão logo na primeira atividade que os estudantes conheceram o GeoGebra versão “móvel”, mostraram o domínio das funcionalidades do aplicativo exigidas para a exploração das questões. Os grupos mostraram-se interessados e todos conseguiram realizar as atividades. Após a familiarização com o software, a exploração das questões, ao invés de apenas respostas estáticas, do tipo efetuar cálculos e informar a resposta final, os alunos conseguiram construir hipóteses, conjecturar e explorar as características dos objetos matemáticos em debate.
A sequência de atividades foi realizada em grupos. Pressupõe-se que essa escolha de organização dos estudantes no momento das atividades favoreceu e forneceu elementos que evidenciam uma aprendizagem matemática. Observou-se que um ambiente em que os sujeitos em conjunto realizam as atividades oportuniza o surgimento de diálogos que os conduzem à elaboração de argumentos. Ademais, essas interações oportunizaram aos alunos conversar entre si sobre matemática. Novamente destaca-se que a partir do processo dialógico entre os estudantes e mediados pela professora fizeram emergir a criação, teste, validação/reorganização de conjecturas.
Nota-se que a utilização da tecnologia móvel por meio de um aplicativo que os sujeitos pudessem interagir entre si e com o artefato tecnológico foi o meio para que acontecessem os diálogos. Ao utilizar o GeoGebra Graphing Calculator nota- se que o "movimento" fornecido aos elementos predominantemente estáticos nos livros didáticos oportunizou aos estudantes conduzir o processo da própria aprendizagem, ou seja, a partir de suas palavras elaborar o seu próprio entendimento sobre a matemática que estavam estudando.
Portanto, uma consequência e contribuição da presente pesquisa é olhar para o diálogo entre os pares na sala de aula como elemento necessário para a aprendizagem da matemática. Notou-se que oportunizar momentos de compartilhamento e enfrentamento de situações de forma conjunta é profícuo para o grupo (coletivo) e também benéfico para o sujeito (individual). Tal metodologia de trabalho diametralmente se afasta da prática unidirecional de divulgação dos conhecimentos em sala de aula, e dessa forma, enfatiza-se aqui importância de se trabalhar em sala de aula atividades de forma conjunta e com características cooperativas.
6. Referências Bibliográficas
AMARAL, A.; FILHO, J.M.; NOGUEIRA, R.E. O Uso do Geogebra no Estudo da Função Quadrática. II Congresso Nacional de Formação dos Professores; XII Congresso Estadual Paulista sobre Formação de Professores. 2014. Disponível em: <https://repositorio.unesp.br/bitstream/handle/ 11449/141829/ISSN2357-7819-2014-4274- 4286.pdf?sequence=1>. Acesso em junho de 2017.
ARAÚJO, J.E.; SILVA, J.V.N. Uma abordagem sobre o estudo de funções quadráticas usando o GeoGebra. Anais do Congresso Nacional de Pesquisa e Ensino em Ciências, 2016. Disponível em: <http://www.editorarealize.com.br/revistas/ conapesc/trabalhos/TRABALHO_EV058_MD4_ SA91_ID782_10052016213929.pdf>. Acesso em junho de 2017.
BOGDAN, R.; BIKLEN, S. Investigação Qualitativa em Educação: uma introdução à teoria e aos métodos. Porto Editora. Porto. 1994.
BONA, A.S. Espaço de aprendizagem digital da matemática: O aprender a aprender por cooperação. Tese de Doutorado. Universidade Federal do Rio Grande do Sul, Porto Alegre, 2012. Disponível em: <http://www.lume.ufrgs.br/handle/ 10183/63132>. Acesso em julho de 2017.
BONA, A.S.; LUTZ, M.R. Explorando os coeficientes da função quadrática por meio do software Winplot: Uma experiência com alunos do 2º ano do Ensino médio. Revemat. Florianópolis (SC), v. 10, n. 2, pp. 209-226, 2015. Disponível em: <https://periodicos.ufsc.br/index.php/revemat/ article/view/40105>. Acesso em junho de 2017.
BORBA, M. C.; GADANIDIS, G.; SILVA, R. S. R. Fases das Tecnologias Digitais em Educação Matemática. 1. Editora Autêntica Editora. Belo Horizonte. 2014.
BORBA, M. C.; PENTEADO, M. G. Informática e Educação Matemática. 2. Editora Autêntica Editora. Belo Horizonte. 2002.
BORTOLOSSI, H. J.; PESCO, D.U.; REZENDE, W.M. Explorando aspectos dinâmicos no ensino de funções reais com recursos do GeoGebra. Anais da 1ª Conferência Latino Americana de Geo- Gebra, pp. 74-89, 2012. Disponível em: <https:// revistas.pucsp.br/index.php/IGISP/article/ view/8370/6580>. Acesso em junho de 2017.
BRASIL. Ministério da Educação. Orientações Educacionais Complementares aos Parâmetros Curriculares Nacionais (PCN+). Ciências da Natureza e Matemática e suas tecnologias. Brasília. 2002. Disponível em: <http://portal.mec. gov.br/seb/arquivos/pdf/CienciasNatureza.pdf>. Acesso em julho de 2017.
BRASIL. Ministério da Educação. Orientações Educacionais Complementares aos Parâmetros Curriculares Nacionais. Bases legais. Brasília. 1999. Disponível em: <http://portal.mec.gov.br/seb/ arquivos/pdf/ciencian.pdf>. Acesso em julho de 2017.
CAIRES, J.B.S.; NASCIMENTO, J.C. Um estudo de funções polinomiais de 1º e 2º graus em ambiente informatizado. Revista Eventos Pedagógicos, Cáceres, v. 3, n. 3, pp. 390-409, Ago-Dez. 2012. Disponível em: <http://sinop.unemat.br/ projetos/revista/index.php/eventos/article/view- File/946/677>. Acesso em junho de 2017.
CAMARGO, L.S.; BECKER, M.L.R. O Percurso do Conceito de Cooperação na Epistemologia Genética. Revista Educação & Realidade. Porto Alegre, v. 37, n. 2, pp. 527-549, maio/ago, 2012. Disponível em: <http://seer.ufrgs.br/educacaoerealidade/ article/view/17341>. Acesso em outubro de 2017.
COLET, E.B. Uma nova proposta para o ensino de funções quadráticas. Curso de Especialização em Matemática, Mídias Digitais e Didática para a Educação Básica. Instituto de Matemática e Estatística. Universidade Federal do Rio Grande do Sul, 2015. Disponível em: <https://www.lume.ufrgs.br/bitstream/handle/ 10183/134088/000983935.pdf?sequence= 1>. Acesso em junho de 2017.
FLICK, U. Introdução à pesquisa qualitativa. Tradução. Joice Elias Costa. 3. ed. Artmed. Porto Alegre. 2009.
GIRALDO, V.A.; GUIMARÃES, L.C.; MURICI, M.L. Funções reais: possibilidades em um ambiente de geometria dinâmica. IV HTEM–Colóquio de História e Tecnologia no Ensino da Matemática, 2008. Disponível em: <http://limc.ufrj.br/htem4/ papers/69.pdf>. Acesso em junho de 2017.
LOPES, S. P. Registros de representações semióticas no estudo das funções polinomiais de segundo grau. Anais do XI Encontro Nacional de Educação Matemática. Educação Matemática: Retrospectivas e Perspectivas. Curitiba- Paraná, 2013. Disponível em: <http://sbem.web1471. kinghost.net/anais/XIENEM/pdf/1554_1454_ ID.pdf>. Acesso em junho de 2017.
MEDEIROS, M.F.; SCHARDOSIM, E. Utilização do Software Geogebra No Ensino E Aprendizagem De Funções Polinomiais Do Segundo Grau. Anais do 3º Simpósio de Integração Científica e Tecnológica do Sul Catarinense. Disponível em: <http://emt2015.pbworks. com/w/file/fetch/94667282/SICT-SUL_Artigo_ 8337549020%20erica.pdf> Acesso em junho de 2017.
PIAGET, J. Estudos Sociológicos. Forense. Rio de Janeiro. 1973.
PIAGET, J. O trabalho por equipes na escolha- Jean Piaget. Revista de Educação. São Paulo, set/dez, 1993. Tradução Luiz G. Fieury. Disponível em: <https://www.ufrgs.br/psicoeduc/piaget/o-trabalho- por-equipes-piaget/>. Acesso em outubro de 2017.
PINTO, S. R. Ensino de funções quadráticas com o GEOGEBRA Graphing Calculator na escola básica: um olhar para a cooperação entre os estudantes. Trabalho de conclusão de curso. Universidade Federal do Rio Grande do Sul, Porto Alegre, 2018. Disponível em: <http://hdl. handle.net/10183/179453>. Acesso em junho de 2018.
RICARDO, J.C. Uma proposta para o ensino de funções quadráticas mediada pela tecnologia: um estudo de caso. Vassouras, 2012, 135 p. Dissertação, Universidade Severino Sombra. Pós- Graduação Stricto-Sensu em Educação Matemática. Disponível em: <http://www.uss. br/arquivos/posgraduacao/strictosensu/educacaoMatematica/ dissertacoes/2012/Dissertacao_Jonas_ FichaOK.pdf>. Acesso em junho de 2017.
SANTOS, L.V.; SILVA, A.C.; SOARES, W.A. Utilização do Winplot como software educativo para o ensino de matemática. Revista Diálogos, Revista de Estudos Culturais e da Contemporaneidade, n. 6, pp. 187-206. 2012. Disponível em: <http:// www.revistadialogos.com.br/Dialogos_6/Dialogos_ 6_Willames_Adriano_Luciana.pdf>. Acesso em junho de 2017.
SILVA, W.R. Aplicação do GeoGebra no estudo de funções quadráticas. Revista Digital FAPAM, Pará de Minas, v. 5, n. 5, pp. 160-185, 2014. Disponível em: <http://fapam.web797. kinghost.net/periodicos/index.php/synthesis/ article/view/87/82>. Acesso em junho de 2017.
Licença
Gôndola, Ens Aprend Cienc. é uma publicação de acesso aberto, sem encargos econômicos para autores ou leitores. A publicação, consulta ou download do conteúdo da revista não gera nenhum custo para autores ou leitores, uma vez que a Universidade do Distrito Francisco José de Caldas assume os custos relacionados à edição, gerenciamento e publicação. Os pares avaliadores não recebem nenhuma compensação econômica por sua valiosa contribuição. O trabalho de todos os atores mencionados acima é entendido como uma contribuição para o fortalecimento e crescimento da comunidade de pesquisa no campo do Ensino de Ciências.
A partir de 1º de dezembro de 2018 o conteúdo da revista são publicados sob os termos da Licença Atribuição-NãoComercial-CompartilhaIgual 4.0 Internacional (CC BY-NC-SA 4.0), sob a qual outros podem distribuir, remix, tweak , e criar a partir do trabalho de forma não comercial, desde que eles dêem crédito e licenciam suas novas criações sob as mesmas condições.
Os detentores dos direitos autorais são os autores e a revista Góndola, Ens Aprend Cienc. Os proprietários mantêm todos os direitos sem restrições, respeitando os termos da licença relativa à consulta, download e distribuição do material.
Quando o trabalho ou qualquer um dos seus elementos estiver no domínio público de acordo com a lei aplicável, esta situação não será afetada pela licença.
Da mesma forma, incentivamos os autores a depositar suas contribuições em outros repositórios institucionais e temáticos, com a certeza de que cultura e conhecimento são bons para todos e para todos.





















