DOI:
https://doi.org/10.14483/23464712.5020Publicado:
2013-01-01La modelación matemática en situaciones cotidianas con los software Avimeca y Mathcad
Mathematical modeling in daily situation with Avimeca and Mathcad Software
Palabras clave:
Problem solving, Mathematics Modeling, Colaborative Group. (en).Palabras clave:
Resolución de problemas, Modelación Matemática, Grupo colaborativo (es).Descargas
Referencias
ALEJANDRO, C. A. Prácticas de Laboratorio de Física General en Internet. Revista Electrónica de Enseñanza de las Ciencias. 3(2), 202-210. 2004.
AMIYA TT-01 XB-PRO 4WD SUBARU, MOTOR EZRUN 9T 35A 4300 KV. Disponible en: <http://www.cochesrc.com/foros/1-10-y-1-12-pista-y-touring-electrico-520/post-tamiya-xb-pro-tt-01-a-1624860/index42.html#ixzz1ya4KCNYw. Visitado en: 29, Jul., 2012.
AVIMÈCA. Disponible en: http://www.acrennes.fr/pedagogie/scphys/outinfo/log/avimeca/am_h.htm> Visitado en: 29, Jul., 2012.
CAÑAL, P. La investigación escolar hoy. ALAMBIQUE. 52, 9-19. 2007.
EZQUERRA, A. Utilización de vídeos para la realización de medidas experimentales. ALAMBIQUE, 44, 113-119. 2005
EZQUERRA, Á., ITURRIOZ, I., DÍAZ, M. (2011). Análisis experimental de magnitudes físicas a través de vídeos y su aplicación al aula. Revista Eureka sobre Enseñanza y Divulgación de las Ciencias. 9 (2), 252-264. 2012
FONT, A. Las líneas maestras del aprendizaje por problemas. 2004. Pag. 3. Disponible en: http://www.ub.edu/mercanti/abp_ejes.pdf . Visitado en: 17, Ene., 2013.
HITT, F. Funciones en contexto. Proyecto sobre visualización matemática. Departamento de Matemática Educativa. Mexico. 2000.
HITT, F., CORTÉS, J. C. Planificación de actividades en un curso sobre la adquisición de competencias en la modelización matemática y uso de calculadora con posibilidades gráficas. Revista digital Matemática, Educación e Internet. Vol. 10, No 1. 2009. Disponible en: http://www.cidse.itcr.ac.cr/revistamate/. Visitado en: 18, Ene., 2009
LEÓN DEL BARCO, B. La eficacia del aprendizaje cooperativo: entrenamiento en habilidades sociales y dinámicas de grupo. Tesis doctoral. Departamento de Psicología y Sociología de la Educación, Universidad de Extremadura. 2002
MARZANO, R. J. and PICKERING, D. J. Dimensions of Learning Teacher's Manual. ASCD - Association for Supervision and Curriculum Development. Second Edition. 1997.
NORMAN, G. R; SCHMIDT, H. G. The psychological basis of problem-based learning: A review of the evidence. Academic Medicine. 67; 557-565. 1992.
PACHANO, L. y TERÁN, M. La investigación- acción en el aula: tendencias y propuestas para la enseñanza de la matemática en sexto grado. La Revista Venezolana de Educación educere. 171-179, 2005. Disponible en: <http://redalyc.uaemex.mx/pdf/356/35602905.pdf>. Visitado en: 19, Mayo, 2010.
PUIG, L. La resolución de problemas en la historia de las matemáticas En Aymerich, José V. y Macario, Sergio (Eds.) Matemáticas para el siglo XXI. Castellón: Publicacions de la Universitat Jaume I. ISBN: 84-8021-551-8. pp. 39-57. 2006.
STEPIEN, W. J. Problem-based Learning: As authentic as It Gets. Educational Leadrship. 50, No 7: 25-28. 1993.
Cómo citar
APA
ACM
ACS
ABNT
Chicago
Harvard
IEEE
MLA
Turabian
Vancouver
Descargar cita
GÓNDOLA
ISSN 2145-4981
Vol 8 No 1 Enero-Julio de 2013.
LA MODELACIÓN MATEMÁTICA EN SITUACIONES COTIDIANAS CON LOS SOFTWARE AVIMECA Y MATHCAD
Mathematic modelation in daily situations with Avimeca and Mathcad softwares
Rafael Pantoja Rangel1
Ricardo Ulloa Azpeitia2
Elena Nesterova3
1Contato: rpantoja@prodigy.net.mx
2Contato: ricardo.ulloa@cucei.udg.mx
3Contato: elena.nesterova@cucei.udg.mx
Resumen
Los procesos de modelación a través del planteamiento de relaciones funcionales, son considerados tanto por estudiantes y profesores, como tareas difíciles, ya que las actividades requieren de una destreza eficiente y creativa para articular y manejar diferentes representaciones de una situación de la vida cotidiana y relacionarlas con la modelación matemática. Además del bagaje de conocimiento matemático que los alumnos requieren a la hora de establecer un plan de solución, la resolución de problemas y trabajo colaborativo, son fundamentales para promover el aprendizaje. En este reporte se presentan como situaciones de la vida cotidiana, el llenado de recipientes, el atletismo y el ciclismo, y se trata de que el estudiante identifique las relaciones entre las variables que intervienen, así cómo determinar la función que modela su comportamiento. La actividad se filma en video, y con el software AVIMECA se obtienen datos en tiempo real del video, mismos que se tratan con Excel y se seleccionan para obtener su representación gráfica: tiempo-distancia. A partir de estos datos, con el programa MathCad se desarrolla el algoritmo de mínimos cuadrados y obtiene la expresión de la función que modela el fenómeno.
Palabras clave:Resolución de problemas, Modelación Matemática, Grupo colaborativo.
Abstract
Modeling processes through the approach of functional relationships are considered by both, students and teachers, as a difficult task since the activities require efficient and creative skills to connect and manage different representations of a situation of daily life, and relate with mathematical modeling. In addition to the background of mathematical knowledge that students require when establishing a solution plan, problem solving and collaborative work are essential to promote learning. This report presents as everyday life situations activities relating to filling containers, athletics and cycling. The goal is that the student identifies the relationships between the variables involved in the phenomenon and calculate the function that models its behavior. The development of the activity has four stages: The activity is videotaped; the software AVIMECA is used to get data variables in real time; the graphical representation of data is carried out with Microsoft Excel; and finally the software MathCad is used to calculate the mathematical expression that models.
Keywords: Problem solving, Mathematics Modeling, Colaborative Group.
Introducción
Como lo señala Ezquerra (2011), el desarrollo de la ciencia a lo largo de la historia se ha apoyado en dos pilares fundamentales: la observación y la experimentación. Sin embargo, estos pilares parece que a los actores de la enseñanza y aprendizaje se les ha olvidado incluirlos en el aula, como si el conocimiento matemático sólo existiera en la forma acabada como se presenta en los libros o en el discurso de profesor, donde lo algorítmico prevalece por encima de los acercamientos verbales, numéricos o gráficos. Enunciados como los siguientes se escuchan en las aulas, “Factoriza la expresión siguiente”, “Deriva la función siguiente” o “Integra por fracciones parciales la función siguiente” o “Dados los datos siguientes aproxima un polinomio de tercer grado”, que son propios del proceso algorítmico que ha permeado el sistema educativo por un largo tiempo.
De la misma forma, los alumnos se han planteado siempre preguntas como las siguientes: ¿Y para qué sirven las matemáticas?, ¿De dónde se obtiene las función? o ¿Cómo se obtuvieron los datos del problema y qué representan?, ¿En qué situaciones de la vida cotidiana se aplica la integración por fracciones parciales? Según Alejandro (2004) y Cañal (2007) es esencial que los alumnos realicen prácticas de laboratorio, en el que participe, que se entere que la matemática está presente en nuestra vida diaria tendiente a fomentar el interés por la investigación temprana.
Así que en el curso de Métodos Numéricos de las carreras de ingeniería del Instituto Tecnológico de Ciudad Guzmán, se les planteó a los alumnos que investigarán varias situaciones en contexto, apoyados en el Aprendizaje Basado en Problemas (ABP) y el Aprendizaje Colaborativo (AC), como se sugiere en el modelo educativo para el siglo XXI del Sistema Nacional de Institutos Tecnológicos (2012). Las situaciones problema (HITT, 2009) planteadas a los alumnos fueron el llenado de recipientes, el “despeje” de un balón de futbol, el “tiro” a un aro en el basquetbol, el movimiento de un ciclista y de un corredor, con la finalidad de que identificaran las relaciones existentes entre las variables que intervienen en la situación problema, como pueden ser la distancia recorrida y el tiempo.
El ABP es un enfoque didáctico basado en el principio de usar problemas, categorizados como abiertos o cerrados como punto de partida para la adquisición, integración y transferencia de nuevos conocimientos, pero en forma estricta, en esta investigación se utilizará sólo en forma parcial, dado que el objetivo no es someter a los alumnos a problemas abiertos, sino que son situaciones problema de la vida cotidiana, para que el alumno se adentre en la modelación matemática, mediante el diseño del escenario para la grabación del video (EZQUERRA, 2005), la toma de datos, la identificación de las variables y la función que mejor se ajuste los datos obtenidos.
El interés relacionado con la solución de problemas, no es nuevo, ya Puig (2006) señala que se tiene conocimiento de diversos problemas desde hace 3000 años a. c. en Babilonia, así que lo nuevo en la actualidad, es el énfasis que se ha puesto en el intento de comprender la naturaleza de los procesos que se ponen en juego, por ejemplo, cuando los alumnos se involucran en el desarrollo de la situación problema, se mejora la transferencia de conceptos a la solución de nuevos problemas, se incrementa el interés intrínseco en el tema planteado y se promueven habilidades para el aprendizaje autónomo (NORMAN, 1992), condiciones que se evidenciaron cuando al concluir el análisis del llenado del primer recipiente, los alumnos ya para el proceso del quinto recipiente, trataron de intuir la función a obtener, conocimientos previos que extrapolaron hacia la obtención de datos de los movimientos del ciclista y del corredor.
Otro aspecto importante que se tomó en consideración, es que los alumnos que utilizan como estrategia la resolución de problemas, obtienen tanta información y logran un incremento significativo en su aprendizaje, y muchas veces más, que los alumnos de las clases tradicionales (STEPIEN, 1993), porque les permite usar la información de manera significativa (MARZANO, 1997), además de que se deja de medir el aprendizaje en horas de docencia para hacerlo en horas de esfuerzo realizado por los alumnos para adquirir determinados conocimientos, expresados en horas de aprendizaje (FONT, 2004).
Los alumnos trabajaron en base a pequeños equipos de trabajo, aprenden en forma colaborativa con la finalidad de socializar sus conocimientos tendientes a lograr objetivos en común, mientras que el papel del profesor se transforma en facilitador del aprendizaje y ocupa un lugar importante en el desarrollo del proceso. León Del Barco (2002) reporta que los grupos que son menos habilidosos socialmente obtienen puntuaciones más bajas en las escalas y los grupos más habilidosos socialmente obtienen puntuaciones medias más altas en las escalas.
Pachano y Terán de Serrentino (2005) destacan que fundamentalmente el logro de aprendizajes significativos, se debe a la interacción alumno-alumno y alumno-profesor producto del trabajo en grupo y la prevalencia de un clima positivo en el aula de clase, en el que se propicia un enriquecimiento del aprendizaje como producto de la interacción, la participación, la colaboración, la motivación y la creatividad, a través de sus concepciones, de sus experiencias previas y de la ayuda de los otros, para construir paulatinamente el conocimiento matemático. En este caso, la situación problema se planteó para desarrollarla fuera del aula, pero no desestimó para nada el trabajo colaborativo porque se identificó durante el proceso el desarrollo de actitudes positivas, habilidades y destrezas, contribuye a desarrollar y consolidar valores de solidaridad, compañerismo, cooperativismo y convivencia.
El AC tiene que ver con la actividad para aprender del alumno, nunca espontánea, en todo instante orientada, guiada e intencionada, pero con una libertad responsable y comprometida de los aprendices. Además se relaciona con la bidireccionalidad, intencionalidad y trascendencia necesaria en el proceso de enseñanza y aprendizaje, entre el que guía y orienta la actividad y el aprendiz, plantea una forma diferente de relación profesor-alumno y alumno-alumno entre sí, con el proceso conocido como mediación.
Para el estudio tuvieron especial significatividad:
- La resolución de problemas, como elemento central del tema de ajuste de datos en el curso de Métodos Numéricos.
- Las tendencias actuales de la educación, que coinciden en que el aprendizaje y transferencia de conocimientos se mejoran al utilizar actividades significativas para el alumno y,
- el empleo del aprendizaje colaborativo con la guía de un facilitador, con la alternativa del enfoque didáctico del ABP.
Metodología
Al inicio de la fase experimental el equipo colaborativo discutió acerca de cómo es la función que describe el llenado del primer recipiente, conjeturas que se extendieron hasta los otros cuatro recipientes, que inclusive los describieron de la siguiente forma:
- Un cilindroide es un recipiente cuya forma geométrica corresponde a un cilindro de superficie alabeada y estrecho en la parte media, por simple inspección se puede considerar que la función que podría describir el llenado es una (función) lineal con cierta inclinación hacia el tiempo, en una gráfica de altura contra tiempo, debido a lo estrecho que el recipiente presenta en la parte media, y por consecuencia el llenado será en menor tiempo.
- El paraleloide, debido a que tiene forma de paralelepípedo (Nota: definimos así a nuestro recipiente debido a su semejanza pero no es un paralelepípedo).
- El pepinoide llamado así por las semejanzas presentadas a un pepino (fruta), es un recipiente cuya forma geométrica es muy parecida a la de un de cilindro por una cierta diferencia de que está un poco más grande del centro este recipiente. Es muy al contrario del cilindroide ya que es este recipiente presentará en su función el llenado lineal con cierta inclinación hacia el tiempo.
- Un globoide, así definido en esta práctica, es un recipiente parecido geométricamente a la forma de un globo y tiene un terminado en forma cilíndrica que es donde está localizada la boca. De acuerdo a la imagen del globoide podemos inferir, a manera de predicción, que en su boquilla tendrá una función con comportamiento de función exponencial ya que es grande la esfera contenida en la parte inferior y el pequeño cilindro es relativamente pequeño por lo tanto crecerá con mayor rapidez.
- El último recipiente, llamado peroide, a diferencia de los otros 4 analizados, presenta una arquitectura de diferentes formas a lo largo del mismo, sin embargo, a pesar de la dificultad que pretende representar, se verá que en realidad el modelado de su llenado no es un gran reto. Como se puede observar, el recipiente tiene una forma parecida a lo que es una esfera aplastada por dos de sus extremos (Una figura cilíndrica parecida a una dona) y finalmente, en la parte superior, lo que pareciera una probeta con ciertos ensanchamientos.
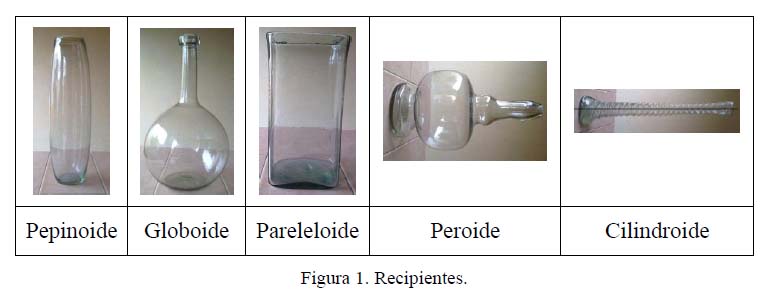
Los alumnos desconocían el funcionamiento del programa AVIMECA (ver Figura 2), sin embargo, se les dejó que investigaran todo lo concerniente al manejo y después de varios intentos, lograron la grabación y la obtención de datos. En el comentario siguiente, los estudiantes denotan que se adentraron en la propuesta:
Se hicieron las pruebas necesarias, se analizaron los datos y finalmente se agruparon de forma tal que se obtenía una función que representaba el llenado de los recipientes y, como se pudo observar, para obtener un resultado fiable, es necesario de un buen software, una cantidad de datos significativa y sobre todo, mucha paciencia.
El formato que maneja el AVIMECA para el video es el AVI, con el Codec by Radius como compresor. Para relacionar la equivalencia entre las medidas reales con las de computador, se efectúa una simple regla de tres, entre las estimadas de la escala real del evento y la resolución del video digital. Por ejemplo, en caso de que la cámara de video tenga una resolución de 640 pixeles de longitud (AMIYA, 2006) y el marco de medida hace 70 cm de longitud, entonces esta medida corresponde aproximadamente a 45 pixeles, es decir,
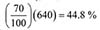 Un error de 1 pixel corresponde a un error del 2.22 %, ie,
Un error de 1 pixel corresponde a un error del 2.22 %, ie,
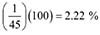 En esto radica la importancia de seleccionar la escala de medida más adecuada a cada situación problema, ya que será el reflejo de las medidas reales, comparadas con las medidas del video digital.
En esto radica la importancia de seleccionar la escala de medida más adecuada a cada situación problema, ya que será el reflejo de las medidas reales, comparadas con las medidas del video digital.
Una vez que se ha tomado el video, se ejecuta el programa AVIMECA y se abre el video para proceder a la obtención de datos. Se seleccionan los ejes coordenados y se ubican sobre el video, en la parte más conveniente a medir. Ahora, durante la toma del video se han marcado algunos puntos importantes para la medición, mismos que serán marcados en el programa AVIMECA, para obtener los datos. Se calibran las dimensiones de la imagen por la selección de dos puntos con el ratón y se asigna la distancia en metros entre los dos puntos elegidos, para posteriormente señalar las posiciones sucesivas con un clic. Por cada clic del ratón sobre el video, en el momento de procesarlo con el AVIMECA, se registran los datos en la tabla anexa al espacio donde se observa el video, hasta que el usuario decida dejar de tomar datos o concluya el video. Finalmente los datos se copian al programa Excel. En este caso se seleccionaron y se exportaron al programa MathCad para desarrollar el método de mínimos cuadrados y obtener la función polinomial que se aproxime mejor a los datos obtenidos. En la figura 3, se presenta el llenado del paraleloide y la tabla donde se registran los datos.
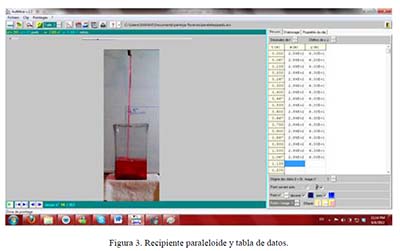
En la Figura 4 se presenta la gráfica realizada en MathCad, para el Cilindroide y sólo algunos de los datos seleccionados aleatoriamente por cuestiones de espacio. Los 1095 datos obtenidos con el AVIMECA se exportaron y refinaron con el programa Excel y con el MathCad se aplicó el método de mínimos cuadrados, dado que es importante para el curso que se cumpla con lo señalado en el programa de Métodos Numéricos vigente del ITCG y el alumno desarrolle el proceso algorítmico que implica.
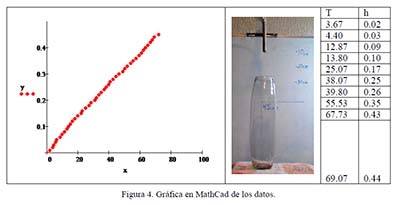
Resultados
Los alumnos iniciaron la discusión colaborativa con un cuestionamiento:
¿Cómo saber la relación matemática y las variables que intervienen en el llenado de un recipiente? Con las regresiones lineales, cuadráticas, exponenciales, nosotros podemos saber el comportamiento de muchos fenómenos físicos mediante gráficas, las cuales suelen ser precisas con un grado de error mínimo entre el planteamiento matemático y la situación real, así que, suponiendo que tengamos un recipiente cilíndrico y un flujo constante de agua, a la hora de describir su comportamiento mediante una función nosotros podremos predecir en cuanto tiempo estará a determinada altura, fenómeno que se aplica cotidianamente en la industria y en muchas ramas más.
Lo sobresaliente de la polémica es que conduce con simplicidad a la modelación matemática, y que sin haber consultado información referente previa, coincide con lo señalado por Hitt (2000): “a través de las funciones podemos modelar matemáticamente un fenómeno de la vida real, describir y analizar relaciones de hechos sin necesidad de hacer a cada momento una descripción verbal o un cálculo complicado de cada uno de los sucesos que estamos describiendo”.
Los estudiantes diseñaron el espacio físico para empezar a grabar el llenado del recipiente y como se observa en la imagen (ver Figura 5) se ubicó en un lugar plano para evitar accidentes; al fondo se nota la medida que se tomó como referencia y que es importante para relacionar el video digital con las medidas reales del llenado. Para el llenado del recipiente se utilizó un compresor casero ideado por los estudiantes, que no causara tanto movimiento al momento de llenar el recipiente, que para el paraleloide duró 73 segundos.

Con el programa AVIMECA se procesó el video para obtener los 1095 datos que relacionan el tiempo y la altura de llenado, posteriormente con el Excel se hizo una selección de puntos, ya que por cuestiones físicas de la resolución del video y de la pantalla de la computadora, en la gráfica (ver Figura 6) se sobreponen unos con otros, además de que el AVIMECA no guarda ningún archivo al momento de cerrarlo.
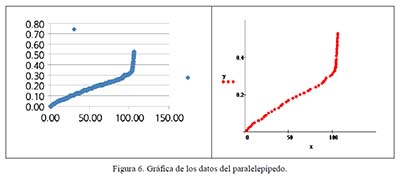
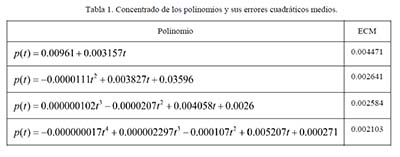
Como se observa en la Figura 6, la gráfica se aproxima por dos curvas, de un tipo hasta cerca de los 100 segundos y otro tipo después de este valor. Con el MathCad los alumnos trataron con diferentes funciones y relacionaron la función obtenida con el proceso de llenado. En la Tabla 1 se presentan cuatro acercamientos en el intervalo [0, 60] en segundos, a los datos para una recta, una parábola, una cúbica y una de cuarto grado con el error cuadrático medio (ECM), calculado por la fórmula:
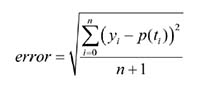
En la Tabla 2 se muestra una parte del procedimiento realizado en MathCad, en el que se soluciona el sistema lineal de dos ecuaciones con dos incógnitas para determinar los coeficientes de la recta de mínimos cuadrados, cuya ecuación se muestra en la tabla 1 y su gráfica en la Figura 7(a). En la Figura 7(b) se presenta la gráfica del polinomio de grado 4.

- El peroide
Cuando se procede al llenado del peroide, los alumnos ya tenían experiencia previa sobre el llenado de los otros cuatro recipientes y sus funciones asociadas, que de manera natural extrapolaron para discutir sobre la forma variada que tiene este recipiente (ver Figura 1) e inician la descripción como sigue:
… podemos ver que por la forma del recipiente nuestra función tendrá, en el principio, una forma más o menos lineal, con algunos cambios en el comienzo y en el final de la parte cilíndrica, esto debido a que en estas zonas estrechas el líquido subirá de manera más rápida, por así decirlo, en comparación con la zona media del cilindro. Luego de que el líquido suba por la parte cilíndrica, pasará por la parte parecida a lo que es una probeta con ciertos ensanchamientos a lo largo de esta, imaginándonos como sería el llenado de esta parte en comparación con la parte cilíndrica, nos daríamos cuenta de que en realidad el nivel del líquido aumentaría considerablemente para un tiempo menor, con ciertos “patrones momentáneos” en los ensanchamientos de esta parte.
Su avance en el llenado y la modelación matemática se refleja en la representación que hicieron antes y después del llenado, que una vez que graficaron los datos obtenidos del tratamiento del video con el AVIMECA se observa que coinciden. ver Figura 10 (a), (b) y (c).
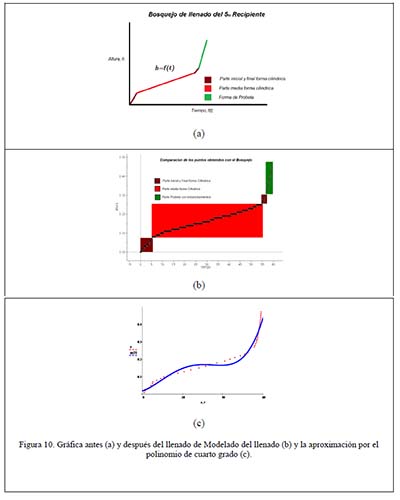
Anteriormente se explica cómo importar los datos arrojados por el Software AVIMECA a una tabla de Excel, así que omitiremos eso para presentar las conclusiones que se tienen al ver el comportamiento de los datos obtenidos. En la Parte cilíndrica del Recipiente, se observa un aumento más o menos lineal, un poco rápido, ya que pasan aproximadamente 1.30 segundos para que se llene apenas 1 centímetro del recipiente en cuestión, pero como se esperaba, conforme se va llenando, necesita más tiempo para subir otro centímetro.
Al ver los datos arrojados por el Software AVIMECA, nos damos cuenta de que en esta parte del llenado, el nivel del líquido sube de manera más acelerada que en la parte cilíndrica, tanto es así que sólo bastaron algunos segundos para que esta fase del llenado se completara. Se presenta la gráfica que describió el llenado del recipiente en cuestión.
- Ciclista
En el caso del ciclista, los alumnos para la experimentación y la toma de video, seleccionaron una cancha de basquetbol en la población de Tecalitlan, Jalisco, ubicada en la región sur del estado de Jalisco. En la Figura 8 se presenta la imagen del ciclista, con los ejes coordenados y la tabla de datos tal y como se trabajó con el video con el AVIMECA.

toma de video, para hacer la equivalencia entre las medidas reales de la cancha del basquetbol y las correspondientes al video, situación que posterioremente se integró al estudio, porque es importante para la toma de datos y que correspondan al movimiento del ciclista en lo real y en el modelo matemático.
Se realizó una selección de datos (Tabla 3) en el intevalo de tiempo [0, 4.14] y se exportaron al MathCad para analizar cual polinomio describe al ciclista hasta que inicia su desaceleración, con un polinomio de tercer grado (ver Figura 8(a)). En la Figura 8(b) se aproximan los datos del tiempo contra distancia con un polinomio de cuarto grado, con un ECM de 0.02.

- El corredor
En la misma cancha de basquetbol se puso a correr a un estudiante de ida y vuelta y se tomó el video de su recorrido y con el AVIMECA se obtuvieron 187 datos, y se les dio el mismo tratamiento con el programa MathCad, para obtener el polinomio de cuarto grado que describe su movimiento, aproximadamente con un ECM de 0.181. ver Figura 9.
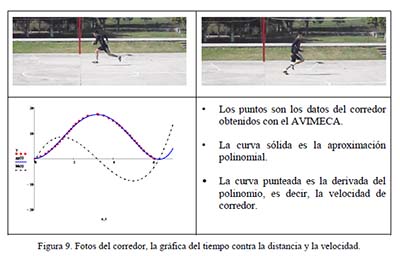
Es claro que el objetivo de los estudiantes no fue realizar el estudio comparativo de cada una de las gráficas con la situación de la vida cotidiana en cuestión, pero conforme se adentraban en la fase experimental ya discutían, identificaban las variables, median el tiempo y opinaban sobre la expresión matemática que modela el fenómeno, entre otras observaciones que evidencian la riqueza de ubicar a los alumnos en una situación problema.
Conclusiones
Se ha planteado la problemática referente a las dificultades que muestran los estudiantes para resolver problemas y trabajar colaborativamente en la modelación de situaciones en el contexto de la vida cotidiana y una vez analizados los reportes de los estudiantes, se considera que lograron el objetivo propuesto, que fue diseñar la fase experimental para grabar el video del llenado de los recipientes, del ciclista y del corredor, identificaron las magnitudes involucradas y establecieron las relaciones al determinar el polinomio que mejor se ajusta a los datos tomados en tiempo real.
La precisión en la modelación de fenómenos físicos puede ser algo complicado, principalmente porque en la vida cotidiana hay pocas cosas que son constantes, esto debido a que todo está en movimiento, son diversas variables a tomar en cuenta si es que se pretende obtener una modelación “exacta”, que con ayuda de las TIC, la resolución de problemas y el trabajo colaborativo, han propiciado que el modelado matemático cada día se introduzca más en el aula.
La modelación matemática se facilita cuando se tienen los conocimientos previos matemáticos identificados en la solución del problema a tratar, cómo en este caso, que se requiere de que el estudiante conozca la solución de sistemas lineales y el método de mínimos cuadrados.
Los profesores tienen la oportunidad de transformar su práctica pedagógica a través del trabajo colaborativo, toda vez que le permite mejorar el aprendizaje de la matemática y propiciar una enseñanza activa, donde el alumno participe de su propio aprendizaje y aprenda a resolver problemas por sí mismo.
Son distintos los tipos de recipiente utilizados para el llenado, ya que unos tenían forma esférica otros cilíndricos entre otras formas y su comportamiento varia por esa razón, unos se modelaron en forma exponencial, otras en forma lineal o bien pueden ser las dos o más formas para un solo recipiente, y por consecuencia, su descripción se aproxima a funciones seccionalmente continuas. La función es uno de los conceptos que más se aplican en la vida cotidiana, en sus diferentes contextos, como son el hogar, la empresa, el campo, el sector salud, entre otras.
El programa AVIMECA es una herramienta que permite obtener datos reales que interesan al estudiante, que refleja mediante una expresión matemática, que ayuda a entender la importancia de las funciones generadas a partir de datos obtenidos.
Referencias
ALEJANDRO, C. A. Prácticas de Laboratorio de Física General en Internet. Revista Electrónica de Enseñanza de las Ciencias. 3(2), 202-210. 2004.
AMIYA TT-01 XB-PRO 4WD SUBARU, MOTOR EZRUN 9T 35A 4300 KV. Disponible en:
CAÑAL, P. La investigación escolar hoy. ALAMBIQUE. 52, 9-19. 2007.
EZQUERRA, A. Utilización de vídeos para la realización de medidas experimentales. ALAMBIQUE, 44, 113-119. 2005
EZQUERRA, Á., ITURRIOZ, I., DÍAZ, M. (2011). Análisis experimental de magnitudes físicas a través de vídeos y su aplicación al aula. Revista Eureka sobre Enseñanza y Divulgación de las Ciencias. 9 (2), 252-264. 2012
FONT, A. Las líneas maestras del aprendizaje por problemas. 2004. Pag. 3. Disponible en: http://www.ub.edu/mercanti/abp_ejes.pdf . Visitado en: 17, Ene., 2013.
HITT, F. Funciones en contexto. Proyecto sobre visualización matemática. Departamento de Matemática Educativa. Mexico. 2000.
HITT, F., CORTÉS, J. C. Planificación de actividades en un curso sobre la adquisición de competencias en la modelización matemática y uso de calculadora con posibilidades gráficas. Revista digital Matemática, Educación e Internet. Vol. 10, No 1. 2009. Disponible en: http://www.cidse.itcr.ac.cr/revistamate/. Visitado en: 18, Ene., 2009
LEÓN DEL BARCO, B. La eficacia del aprendizaje cooperativo: entrenamiento en habilidades sociales y dinámicas de grupo. Tesis doctoral. Departamento de Psicología y Sociología de la Educación, Universidad de Extremadura. 2002
MARZANO, R. J. and PICKERING, D. J. Dimensions of Learning Teacher's Manual. ASCD - Association for Supervision and Curriculum Development. Second Edition. 1997.
NORMAN, G. R; SCHMIDT, H. G. The psychological basis of problem-based learning: A review of the evidence. Academic Medicine. 67; 557-565. 1992
.PACHANO, L. y TERÁN, M. La investigación- acción en el aula: tendencias y propuestas para la enseñanza de la matemática en sexto grado. La Revista Venezolana de Educación educere. 171-179, 2005. Disponible en:
PUIG, L. La resolución de problemas en la historia de las matemáticas En Aymerich, José V. y Macario, Sergio (Eds.) Matemáticas para el siglo XXI. Castellón: Publicacions de la Universitat Jaume I. ISBN: 84-8021-551-8. pp. 39-57. 2006.
STEPIEN, W. J. Problem-based Learning: As authentic as It Gets. Educational Leadrship. 50, No 7: 25-28. 1993.
Licencia
Góndola, Ens Aprend Cienc. es una publicación de acceso abierto, sin cargos económicos para autores ni lectores. La publicación, consulta o descarga de los contenidos de la revista no genera costo alguno para los autores ni los lectores, toda vez que la Universidad Distrital Francisco José de Caldas asume los gastos relacionados con edición, gestión y publicación. Los pares evaluadores no reciben retribución económica alguna por su valiosa contribución. Se entiende el trabajo de todos los actores mencionados anteriormente como un aporte al fortalecimiento y crecimiento de la comunidad investigadora en el campo de la Enseñanza de las Ciencias.
A partir del 01 de diciembre de 2018 los contenidos de la revista se publican bajo los términos de la Licencia Creative Commons Atribución–No comercial–Compartir igual 4.0 Internacional (CC-BY-NC-SA 4.0), bajo la cual otros podrán distribuir, remezclar, retocar, y crear a partir de la obra de modo no comercial, siempre y cuando den crédito y licencien sus nuevas creaciones bajo las mismas condiciones.
Los titulares de los derechos de autor son los autores y la revista Góndola, Ens Aprend Cienc. Los titulares conservan todos los derechos sin restricciones, respetando los términos de la licencia en cuanto a la consulta, descarga y distribución del material.
Cuando la obra o alguno de sus elementos se halle en el dominio público según la ley vigente aplicable, esta situación no quedará afectada por la licencia.
Asimismo, incentivamos a los autores a depositar sus contribuciones en otros repositorios institucionales y temáticos, con la certeza de que la cultura y el conocimiento es un bien de todos y para todos.









.jpg)




















